一橋橫跨南北，“曲直”變通途

杭仁禮 張毅

[摘? 要] 《普通高中數學課程標準（2017年版2020年修訂）》中對數學文化給予了高度重視，強調要將數學文化融入數學教學活動中，讓學生了解數學的發展歷程，認識數學文化在科學技術和人類社會發展中所起到的重要作用，引導學生認識和感悟數學的科學和文化價值. 文章主要論述了如何利用祖暅原理將求解旋轉體和多面體體積達到完美柔和.

[關鍵詞] 祖暅原理;多面體;旋轉體

初遇問題

在備課過程中，筆者提出：能否構造一個完整的幾何體可以直接求得球的體積呢？鑒于球是高度對稱的幾何體，起初筆者設想構造一個正四面體ABCD，棱長為a.

如果想要利用祖暅原理，構造的幾何體必須滿足三個條件：

①構造的幾何體與球等高;

②構造的幾何體與球的體積相等;

③將構造的幾何體與球放置在同一水平面，用平行于水平面的平面去截幾何體和球，得到的截面積處處相等.

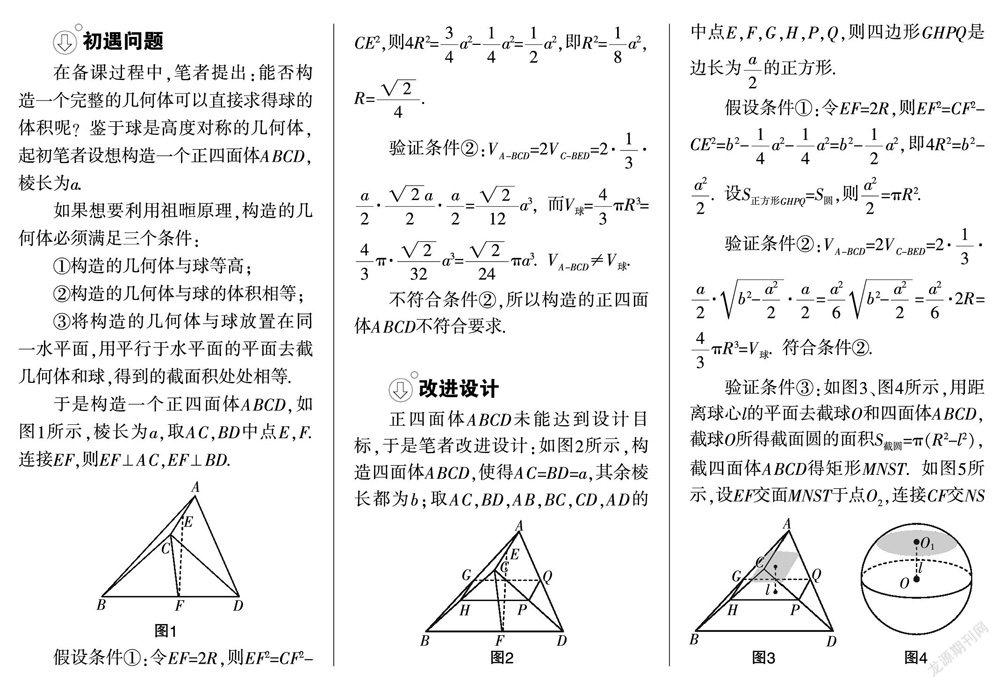
于是構造一個正四面體ABCD，如圖1所示，棱長為a，取AC，BD中點E，F. 連接EF，則EF⊥AC，EF⊥BD.

不符合條件②，所以構造的正四面體ABCD不符合要求.

改進設計

如此，筆者便實現了構造一個多面體、一次性求得球的體積的設想，那么，這樣的結論能否加以推廣呢？

推廣結論

1. 求橢球（橢圓繞其對稱軸旋轉一周所得的幾何體）的體積

方法1：推廣課本的方法，構造幾何體（將圓柱挖去同底等高的倒置圓錐得到的幾何體）.

為此，構造底面半徑為b，高為a的圓柱，從圓柱中挖去一個以圓柱右底面為底面，左底面圓心為頂點的圓錐（如圖7所示），把所得的幾何體與半橢球放在同一個豎平面上.

方法2：構造四面體，一次性完整推導橢球的體積.

構造四面體ABCD，使得AC=BD=m，其余棱長都為n.

上述都是封閉曲線所得的旋轉幾何體，如果是半開放曲線繞旋轉軸旋轉一周所得的幾何體，又該如何求解其體積呢？

2.構造三棱柱，求解拋物線繞其對稱軸旋轉一周所得幾何體的體積

已知拋物線y=x2（0≤y≤m），繞y軸旋轉得到幾何體Z，求該幾何體的體積.

祖暅原理的內容淺顯易懂，只要能構造出可求體積的幾何體，就能求出所需求的幾何體的體積.中華數學文化博大精深、資源豐富，筆者只是從構造多面體的角度求解論證了一些常見的旋轉體的體積，在教學過程中就感悟到了中華優秀傳統文化的歷史自豪感. 這一原理的深化，便是現代高等數學微積分思想.