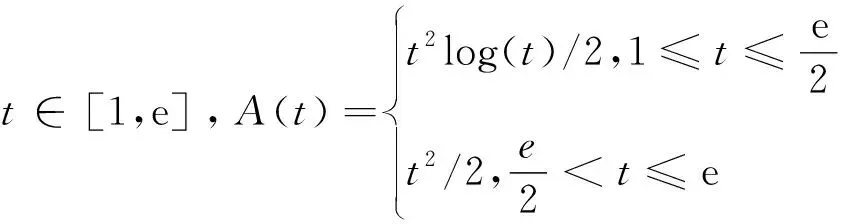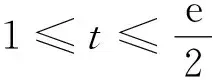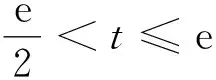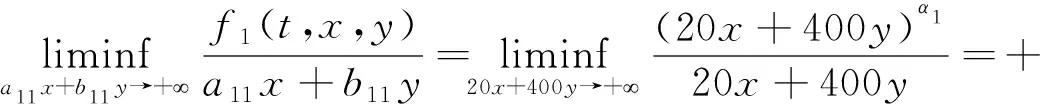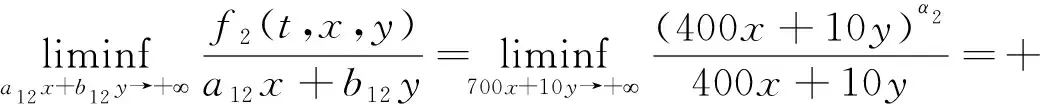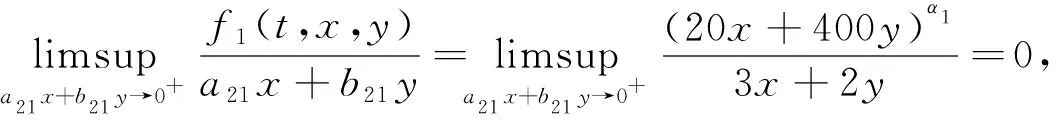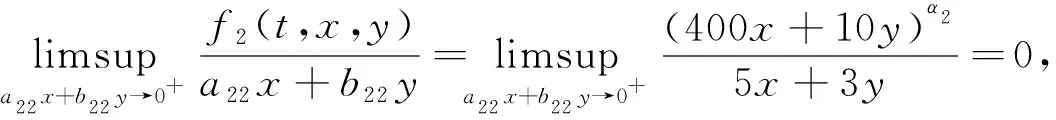具有測度積分邊界條件的非線性Hadamard分數階微分方程的正解
楊尊凱, 顧海波, 李 寧, 孫會賢, 田春平
(新疆師范大學 數學科學學院, 烏魯木齊 830017)
0 引 言
本文主要研究以下具有測度積分邊界條件的非線性Hadamard分數階微分方程:
Dαu(t)+f1(t,u(t),v(t))=0, 1 Dαv(t)+f2(t,u(t),v(t))=0, 1 u(1)=u′(1)=0 (1) v(1)=v′(1)=0 式中:Dα和Iα分別是α階Hadamard分數階導數和積分,2<α≤3,1<σ≤e;A(t)是單調遞增非負的可測函數。假設以下條件成立: H1:fi(i=1,2)在[1,e]×R+×R+上是非負連續函數; H2:在[1,e]上, 近年來,分數階微分方程邊值問題得到了許多學者的關注和深度研究,并且得出了大量的關于分數階微分方程邊值問題的結果。本文研究的 (1) 式正解,尚未有學者進行研究,尤其是具有測度積分邊界的分數階微分方程研究甚少,但也有學者通過使用單調迭代方法研究了分數階微分方程邊值問題解的存在性和唯一性[1-5],文獻[1]通過混合單調算子的不動點定理,研究了含積分邊界條件的奇異分數階微分方程正解的唯一性: [0,+∞)是連續函數,a,h∈C(0,1),A是有界變差函數。 許多學者通過運用不動點定理研究了Caputo 類型的分數階微分方程[6-9],如文獻[6],利用增凹算子的不動點定理,研究了一個新的分數階微分方程組正解的存在性和唯一性: 式中:cDθ10+、cDθ20+是Caputo分數階導數;θi∈(2,3);fi: [0,1]×(-∞,+∞)×(-∞,+∞)→(-∞,+∞)是連續函數;Ai是正可測有界變差函數,ai: [0,1]→[0,+∞)是連續函數,此處i=1,2。近年來,Hadamard類型分數階微分方程也備受學者關注,一些學者通過不動點定理等方法研究了Hadamard類型分數階微分方程[10-15],文獻[10]通過不動點定理研究了具有積分邊界條件的非線性Hadamard分數階微分方程組的正解: 式中:Dβ是β階Hadamard分數階導數,2<β≤3;fi(i=1,2)在[1,e]×R+×R+上是非負連續函數。 定義2.1[15]函數u: [1,∞)→R的α階Hadamard分數階導數定義為: 式中:n=[α]+1;[α]表示實數α的整數部分;log(·)=loge(·)。 定義2.2[15]函數u: [1,∞)→R的α階Hadamard分數階積分定義為: 等式右部分表示積分存在。 引理2.3令x,y∈C[1,e],C[1,e]是指[1,e]上連續函數所構成的空間,積分邊值問題∶ (2) 可以轉換成以下Hammerstein型積分方程: (3) 式中: (4) δ為大于零的常數: 證明對(2)式進行α階積分,有: c1i,c2i∈R,i=1,2,3,再根據u(1)=v(1)=u′(1)=v′(1)=0,所以c12,c13,c22,c23=0,因此可以得到 根據條件: 可以推導出: 即: 令: 那么,c11,c21表示如下: - 類似地,也可以得到: 證明完畢。 通過引理2.3,方程(1)等同于以下Hammerstein型積分方程: (5) 引理2.4對任意的t,s∈[1,e],由式(4)定義的函數G1(t,s)滿足下列不等式: 證明根據文獻[8]的理論結果,令α∈(n-1,n],n∈N,3≤n,構造函數G(z,l): 函數G(z,l)假設如下: (R1)G(z,l)=G(1-l,1-z),對任意的z,l∈[0,1] (R2) Γ(α)k(z)q(l)≤G(z,l)≤(α-1)q(l),對任意的z,l∈[0,1] 因此,對任意的t,s∈[1,e],有∶ Γ(α)k(logt)q(logs)≤G(logt,logs)≤(α-1)q(logs) Γ(α)k(logt)q(logs)≤G(logt,logs)≤(α-1)k(logt) 令z=logt,l=logs,則函數G(z,l)=G1(t,s),所以I1和I2成立,證明完畢。 (6) 令E∶=C[1,e],‖u‖∶=maxt∈[1,e]|u(t)|,P∶={u∈E:u(t)≥0,?t∈[1,e]},由此可知,(E,‖·‖)是實Banach空間,P是E上的錐。通過引理2.3以及引理2.4,定義算子Ti:P×P→P: (7) 對任意的t∈[1,e],有: T(u,v)(t)=(T1(u,v),T2(u,v))(t) (8) Ti:P×P→P,T:P×P→P×P是全連續算子,當且僅當(u,v)是算子T的不動點,因此可以通過(u,v)求解方程(1)。 證明僅證明T1(P×P)∈P0,通過引理2.4(I1)以及Γ(·)函數在[2,+∞)單調遞增,對任意的t∈[1,e],有: 以及 因為α-1>1,所以對任意的u,v∈P,t∈[1,e],有: 證明完畢。 ω-Tω≠λω0, ?λ≥0,ω∈?Ω∩P,那么i(T,Ω∩P,P)=1 引理2.8[16]令E為實Banach空間,P為E上的錐。假設Ω?E是一個有界開集,并且0∈Ω,而 ω-λTω≠0,則i(T,Ω∩P,P)=1 為了后文表述方便,給出如下表示和相關假設條件: H3:存在常數a1i,b1i(i=1,2)≥0以及l1,l2>0滿足下式: H4:存在常數a1i,b1i(i=1,2)≥0以及r1>0滿足下式: 定理 3.1假設條件H1~H4成立,則方程(1)有一個正解。 證明令S1={(u,v)∈P×P:(u,v)=T(u,v)+λ(φ1,φ1),?λ≥0},φ1是P0中一個固定元素,稱S1是P×P中的有界集合,如果存在(u,v)∈S1使得: u(t)=T1(u,v)(t)+λφ1(t),v(t)=T2(u,v)(t)+λφ1(t),t∈[1,e] (9) 那么通過引理2.6,可以知道u,v∈P0。 (10) 通過式(9)對任意的t∈[1,e],有∶ u(t)≥T1(u,v)(t),v(t)≥T2(u,v)(t) (11) 根據算子Ti(i=1,2)的定義以及引理2.4和引理2.5可以得到: (12) (13) 結合條件H3,有: (14) 以及 通過進一步計算可得: 因此,存在常數M1>0,M2>0使得: (15) 這也就證明了S1在P×P中是有界的。如果選擇 則對任意的(u,v)∈?BR1∩P×P,?λ≥0,有: (u,v)≠T(u,v)+λ(φ1,φ1) (16) 成立。因此,通過引理2.7,有: i(T,?BR1∩(P×P),P×P)=0 (17) 接下來證明 (u,v)∈?Br1∩P×P,?λ∈[0,1],(u,v)≠λT(u,v) (18) 假設式(18)不成立,存在(u,v)∈?Br1∩(P×P),λ∈[0,1],使得(u,v)=λT(u,v),這也就意味著對任意的t∈[1,e],有: u(t)≤T1(u,v)(t),v(t)≤T2(u,v)(t) (19) 通過引理2.4以及2.5可得: 將H4代入上述不等式,可得: 因此,可得: 所以,通過H4可以知道∶ i(T,?Br1∩(P×P),P×P)=1 (20) 由式(14)以及式(18)可得: =0-1=-1 令a11=20,a12=700,b11=400,b12=10,a21=3,a22=5,b21=2,b22=3,那么: a11(k1+k3δ)+a12k4≈0.232+0.595<1,b12(k1+k4δ)+b11k3≈0.039+0.252<1 a21(k2+k5δ)+a22k6≈0.429 7+0.535<1,b22(k2+k6δ)+b21k5≈0.056 4+0.016 2<1 ≈1.758 5 a11(k1+k3δ)+a12k4≈0.232+0.623<1,b12(k1+k4δ)+b11k3≈0.116+0.268<1 a21(k2+k5δ)+a22k6≈0.389 7+0.064<1,b22(k2+k6δ)+b21k5≈0.390 6+0.019<1 因此,對任意的t∈[1,e],x,y∈R+,α1,α2>1。令f1(t,x,y)=(20x+400y)α1,f2(t,x,y)=(400x+10y)α2,由此可以得到: 因此條件H3和H4成立。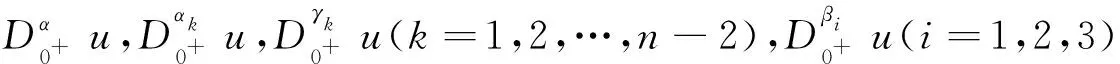
1 預備知識
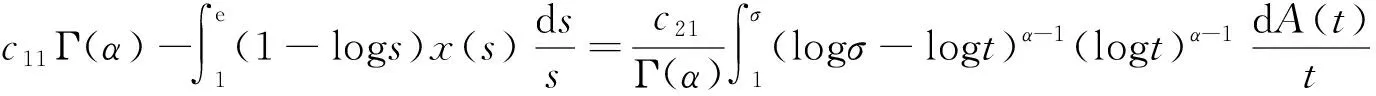
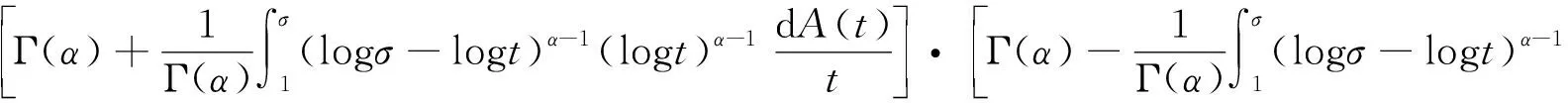

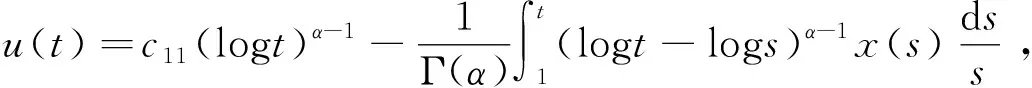
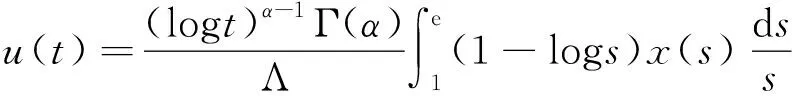
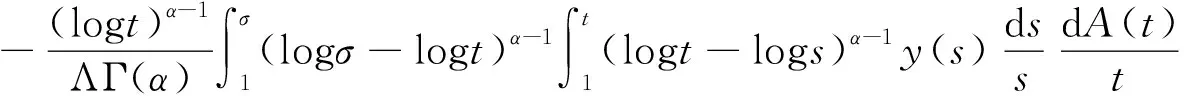
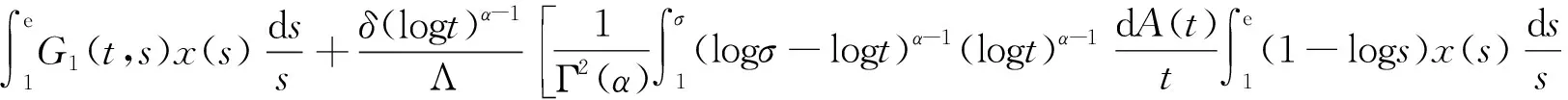
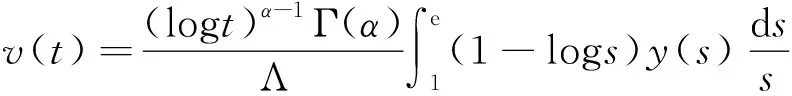
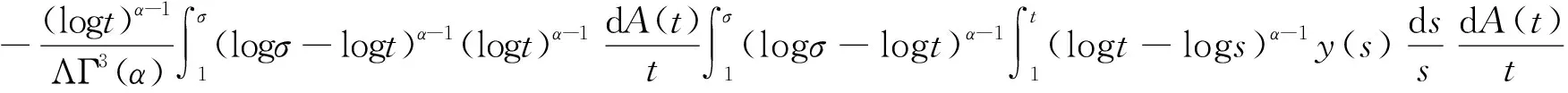
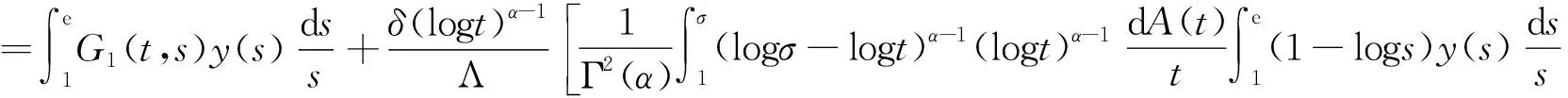
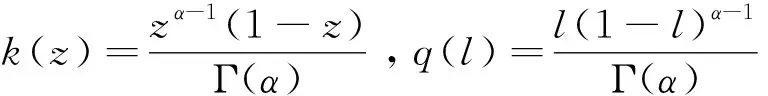
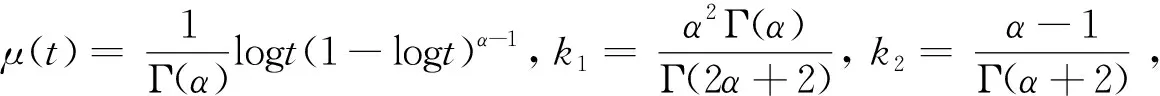
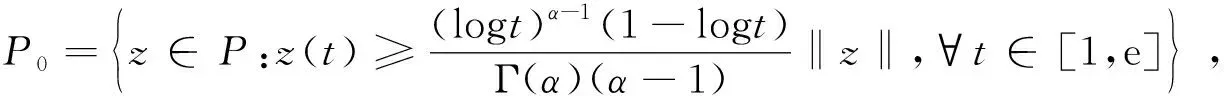
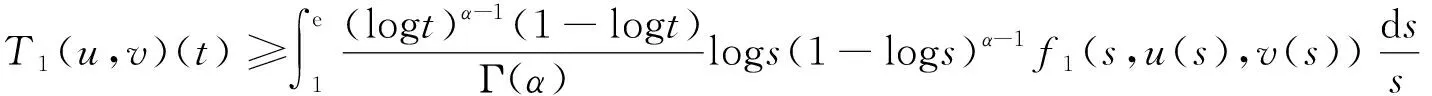
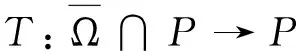
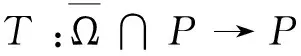
2 主要結果
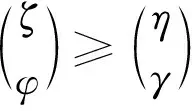
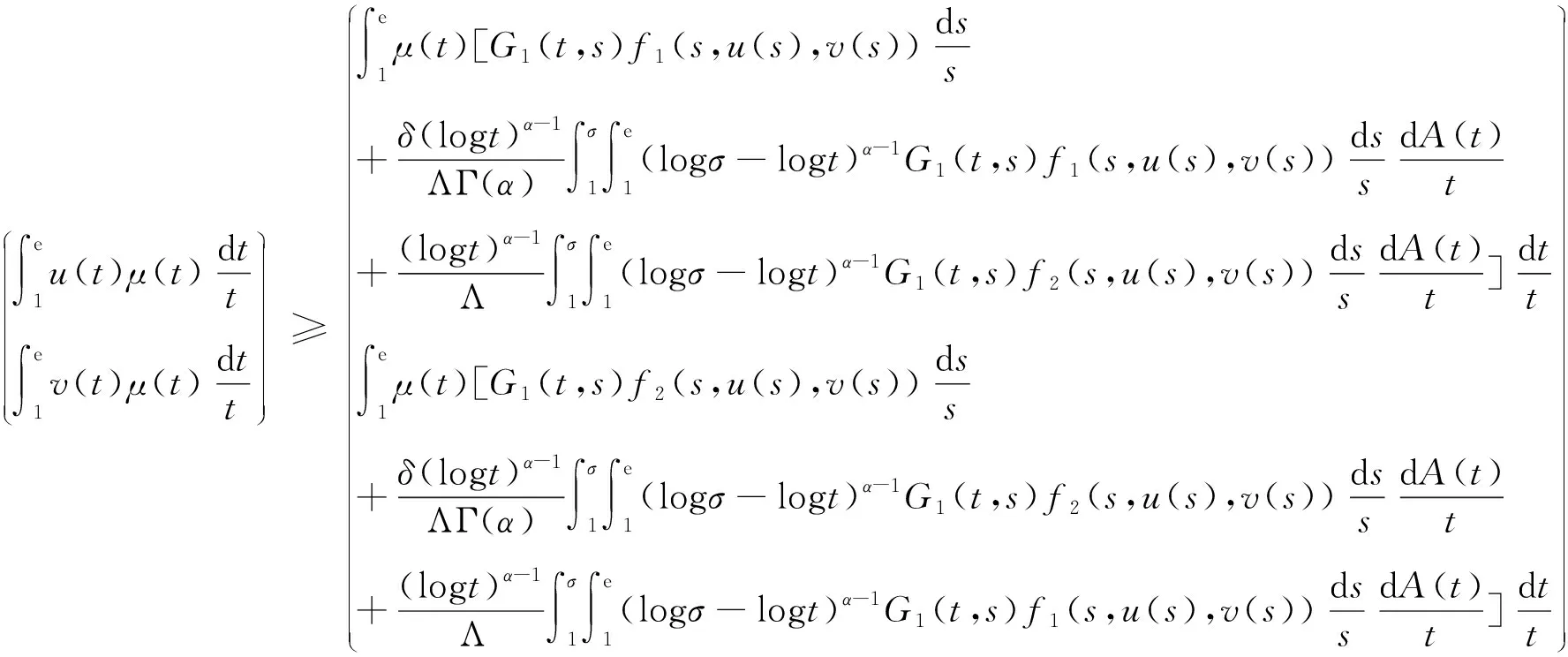
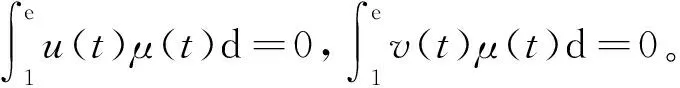
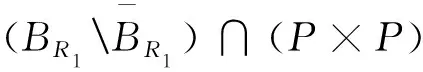
3 例 子