幾類與布朗運動有關的高斯過程的再生核Hilbert空間

艾曉輝, 孫 陽

(1.東北林業大學 理學院, 哈爾濱 150040； 2.哈爾濱理工大學 理學院, 哈爾濱 150080)

0 引 言

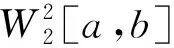
1 預備知識

定義1[14]設H是Hilbert空間，其內元素是非空集合E上復值函數，函數K(s,t)滿足

K:E×E→C

(s,t)K(s,t)

是Hilbert空間H的再生核，其充分必要條件為:

(1) ?t∈E,K(.,t)∈H;

(2) ?t∈E, ?φ∈H， 〈φ,K(.,t)〉=φ(t)。

一個有再生核的復值函數的Hilbert空間叫做再生核Hilbert空間。

這里條件(2)被稱為再生性。通過條件(1)和條件(2)可得：

?(s,t)∈E×E，K(s,t)=〈K(.,t),K(.,s)〉

定義2[15]任意的再生核是正定函數。

2 帶線性漂移的布朗運動的再生核Hilbert空間

定理2.1[16]帶線性漂移的布朗運動X(t)=W(t)+μt，μ∈R+,t∈[0,1]的協方差K(s,t)s,t∈[0,1]為：

K(s,t)=s∧t+μ2st

(1)

證明

K(s,t)=E[X(s)X(t)]

=E[(W(s)+μ)(W(t)+μt)]

=E[W(s)W(t)+W(s)μt+W(t)μs+μ2st]

=E[W(s)W(t)]+E[W(s)]μt+E[W(t)]μs+μ2st

=s∧t+μ2st

定理2.2[14](Mercer定理)若K(s,t)是連續正定函數，則存在特征序列fn(·)∈HR和相應的非負特征值λn，使得：

(2)

(3)

δmn是Kronecker delta函數，有：

(4)

式中，級數在T=(a,b)上一致收斂。

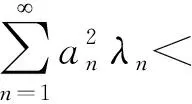
以上定義的內積為:

(5)

定理2.3帶線性漂移布朗運動的KL展開為：

(6)

式中λi，i=1, 2···,n，n∈N，為式(7)所示方程的解：

(7)

證明把帶線性漂移的布朗運動的協方差函數K(s,t)代入等式(2)，得：

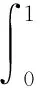
(8)

整理得：

(9)

等式(9)兩邊對t求導,得:

(10)

對等式(10)兩邊同時關于t再次求導，得:

-f(t)=λf″(t)

(11)

整理得

λf″(t)+f(t)=0

(12)

對式(10)求解，可得:

(13)

由式(8)給出的邊值條件，求得:

f(0)=0 時,c2=0

(14)

把c2=0代入式(13),得:

(15)

把式(15)代入式(8),得：

(16)

整理得：

下面利用文獻[9]中 5.2.2 命題2給出帶線性漂移布朗運動以協方差為再生核的Hilbert空間。

定理2.4帶線性漂移布朗運動X(t)=W(t)+μt,μ∈R+,t∈[0,1]以協方差函數K(s,t)作為再生核的Hilbert空間為:

其內積為：

式中:

3 Demeaned布朗運動的再生核Hilbert空間

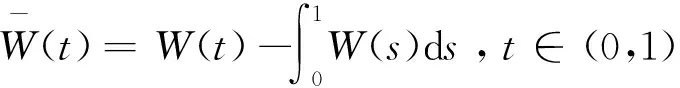
(17)

下面利用文獻[9]中5.2.2的命題1給出Demeaned布朗運動以協方差為再生核的Hilbert空間。

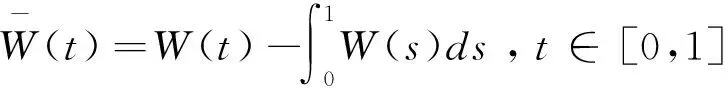
其內積為:

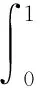
式中

(18)

(19)

其導數為：

(20)

(21)

4 Demeaned布朗橋的再生核Hilbert空間

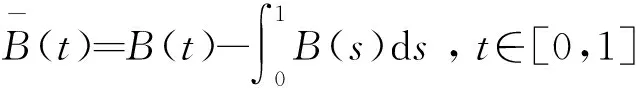
(22)

證明

下面利用文獻[9]中給出Demeaned布朗橋以協方差為再生核的Hilbert空間。

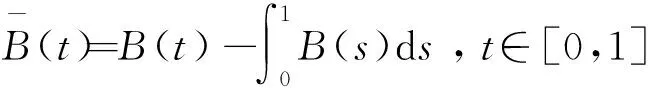
其內積為:

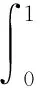
式中

(23)

(24)

其導數為：

(25)

(26)

4 結 論

研究了三類與布朗運動有關的高斯過程再生核Hilbert空間。從協方差函數出發，利用Karhunen-Loève展開理論得到特征函數作為基函數構造再生核Hilbert空間。這項研究豐富了再生核Hilbert空間理論研究，可更好地理解高斯過程協方差函數與再生核Hilbert空間的聯系，為研究高斯過程協方差提供了一種新思路。這項研究還可以從現有的阿基米德數域拓展到p-adic數域展開再生核Hilbert空間理論探索。