GARCH模型的二次加權復合分位數估計①

鐘澤君， 李婷婷

西南大學 數學與統計學院， 重慶 400715

文獻[1-2]提出了廣義自回歸條件異方差(GARCH)模型， 該模型主要用于刻畫資產收益率的波動規律． 文獻[3-4]將GARCH同多種傳統模型進行實證比較， 結果表明GARCH能更為準確地反映我國某些市場的波動情況． 后續學者根據市場特征和需求的不同對GARCH進行了推廣研究， 并演化出了一系列GARCH族模型[5]．

目前， 用于估計GARCH模型參數的方法多種多樣． 文獻[6]將類極大似然(QML)法用于GARCH和ARMA-GARCH模型的參數估計； 文獻[7]將QML法擴展到一系列多維GARCH類模型， 且實證表明其能很好地刻畫匯率序列的波動． 雖然文獻[8]指出QML估計對數據分布具有一定的容錯性， 但其對異常值很敏感， 少量異常值就會對QML估計產生巨大的影響， 也即QML估計并不穩健， 其次， QML法還要求序列4階矩存在， 而金融收益率時序列分布往往呈現出“尖蜂厚尾”的特點， 難以滿足該條件． 由此， 文獻[9]提出了較為穩健的偏差絕對值最小(LAD)法． 文獻[10]提出了基于傳統GARCH模型的分位數回歸估計(QR)法， 并證明了該估計的一致性． 雖然QR估計一定程度上減少了數據尖峰厚尾所造成的估計誤差， 但風險水平的選取將直接影響到QR估計的結果． 因此， 文獻[11]將復合分位數回歸(CQR)應用于估計高頻數據的GARCH參數， 數值模擬結果顯示CQR估計較QR估計更為精確有效． CQR通過綜合考慮多個風險水平下的條件QR使得估計更為穩健有效， 但應對不同的市場損失情況應當賦予不同程度的損失， 故文獻[12]考慮加權復合分位數回歸(WCQR)法， 其通過極小化WCQR參數估計的漸進方差得到權重值， 對于不同分位數回歸給予不同的權重， 以此得到更加穩健有效的估計．

近年來， 受文獻[13]提出的兩步QR思想的啟發， 文獻[14]提出了GARCH模型的混合QR估計， 該估計主要分為兩步： 首先計算QML估計下的條件標準差擬合序列， 接著將此條件標準差擬合序列的倒數作為QR損失的權重得到估計， 數值分析表明混合QR估計可以削弱極端波動的影響， 得到更為精確有效的估計； 文獻[15]還將上述混合QR估計用于探究GARCH-X誤差模型， 數值模擬顯示出該混合估計在大樣本下表現最優． 本文進一步將混合估計擴展到CQR， 結合WCQR思想， 由此提出二次加權分位數回歸(BWCQR)技術． 數值模擬及實證分析表明利用BWCQR估計GARCH模型參數在一定準則下相較已有估計技術更加合理有效．

1 模型及估計

1.1 GARCH模型的BWCQR估計

記yt表示某資產第t天的收益率， 則標準GARCH(p，q)模型為

yt=vtηt

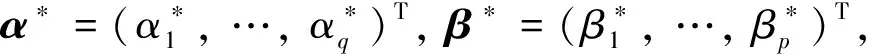
對應GARCH(p，q)模型的條件τk分位數為

(1)

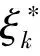
GARCH模型的CQR估計[11]為

(2)

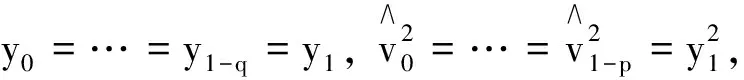
將文獻[12]提出的WCQR擴展至GARCH模型

(3)

將文獻[14]提出的混合QR加權思想擴展到CQR， 由此衍生出估計

(4)

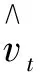
將式(3)和式(4)相整合， 即可得到本文提出的BWCQR估計

(5)

1.2 假設及定理

在給出BWCQR估計的漸進性質之前， 須引入一些記號和模型假設： 記向量a的歐幾里得范數為‖a‖；C表示在不同的計算過程中不盡相同的任一正數； 定義矩陣A=(aij)的歐幾里得范數為‖A‖=∑i，j|aij|；V表示一廣義可積隨機變量； {St}表示一平方可積非負平穩遍歷過程且滿足St∈Ft-1； 變量ρ滿足 0<ρ<1；ρτk(u)關于u的導數為ψτk(u)=τk-I(u<0)．

假設1模型的真值θ*為Θμ的內點， 其中參數空間Θμ定義為

其中實數μ∈(0， 1)且使得θ*∈Θμ．

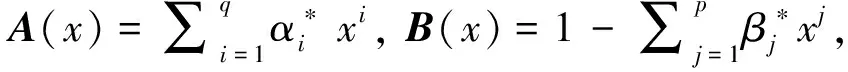
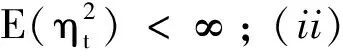
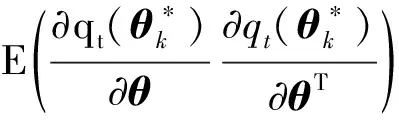
證明分別定義

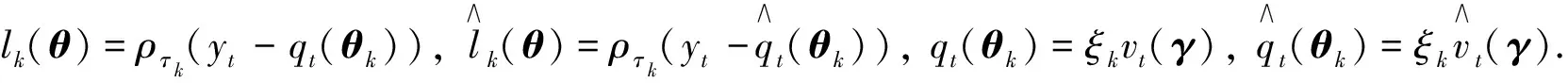
本文主要證明定理2及推論3， 定理1不作詳細證明． 關于定理1可參考文獻[15]中定理1的證明， 分證四點即可：

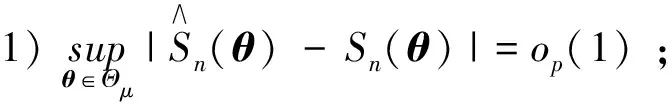
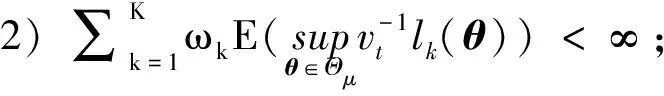
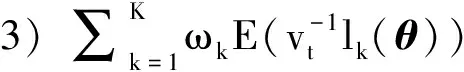
4) 對任一θ#∈Θμ， 當0時有其中B(θ#)={θ#∈Θμ： |θ#-θ|<}表示以θ#為中心為半徑的鄰域．

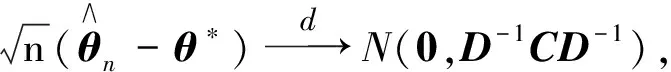
注1當K=1，ω=1且vt=1時， 定理2退化為QR估計的漸進性質， 詳見文獻[10]定理2； 當K=1且ω=1時， 定理2退化為混合QR的漸進性質， 詳見文獻[15]定理2； 當ω=1且vt=1時， 定理2退化為CQR的漸進性質， 詳見文獻[11]定理2．

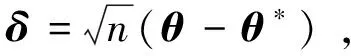
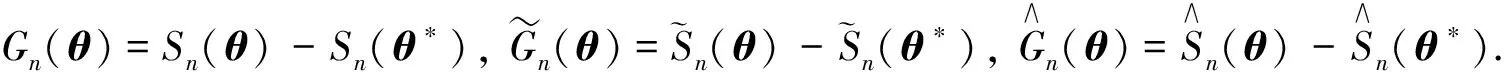
證明

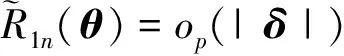
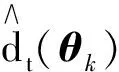
(6)

注意到， 對?τ∈(0， 1)有ρτ(x)≤|x|． 由ρτ(x)的Lipschitz連續性及式(6)， 有

(7)

(8)

因此， 由式(8)及A.2有

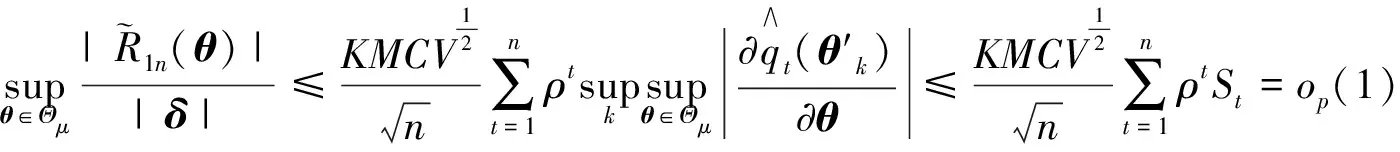
2) 定義

由文獻[16]有等式

(9)

(10)

lk(θ)-lk(θ*)=dt(θk)[-ψτk(ηtk)+Btk]

(11)

據ψτ(x)的定義對其應用Fubini定理及泰勒展開有

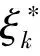
(12)

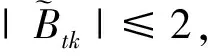
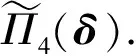
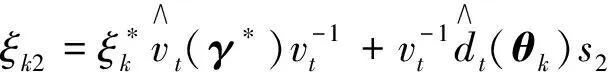
引理2在假設1-3滿足的條件下， 有

證明引理2的證明同引理1的證明類似

據文獻[17]定理3.1和式(9)易證K1n(δ)=op(|δ|)與K2n(δ)=op(|δ|2)．

引理3在假設1-3滿足的條件下， 有

其中

證明由式(9)有

(13)

對R1n(δ)泰勒展開：R1n(δ)=-δTCn-δTK3n(θ′)δ， 其中

定義Btk=Btk1+Btk2， 其中

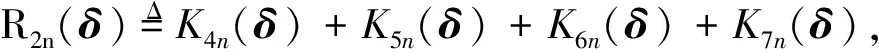
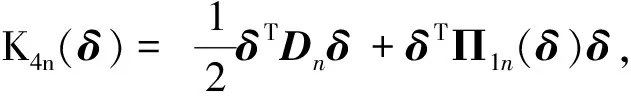
由中值定理、 文獻[10]A.2及假設3， 對?ζ>0

(14)

對K5n(δ)進行放縮后

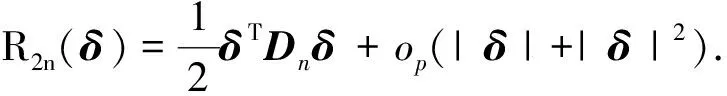
定理2證明結合引理1-3和定理1， 同文獻[15]中定理2的證明類似即可證明該定理．

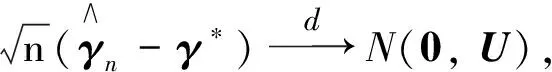
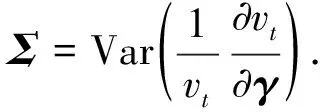
注2令

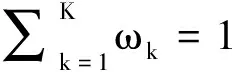
推論1證明矩陣C可分為4塊分塊矩陣

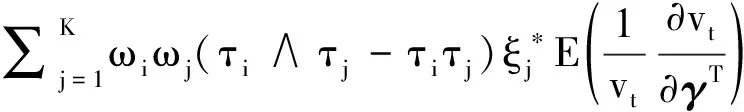
同樣可以將矩陣D分為4塊分塊矩陣

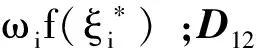
注意到， 在假設4及權重向量ω>0的條件下矩陣D，C均為嚴格正的可逆矩陣， 矩陣D-1CD-1的右下塊(p+q)× (p+q)維矩陣U為

其中

經計算可得推論1成立．

1.3 參數估計步驟

將本文提出的BWCQR分為如下6個步驟：

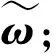
2 數值分析

2.1 蒙特卡洛模擬

基于GARCH(1， 1)模型

利用蒙特卡洛數值模擬檢驗本文所提BWCQR方法在有限樣本下相較QML，QR和CQR方法的穩健性和有效性． 數值模擬模型參數選取如下：

(i) 分別考慮擾動項序列ηt服從標準正態分布N(0， 1)，t(5)分布和t(3)分布；

(ii) 樣本容量分別取n=300，500，1 000和1 500進行300次重復抽樣；

(iii) 復合分位數回歸模型中K值取5，9和19， QR估計的風險水平取0.3，0.5和0.7；

(iv) 本文采用估計量的偏差(Bias)、 標準差(SD)和均方誤差(MSE)作為估計的評價標準．

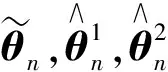
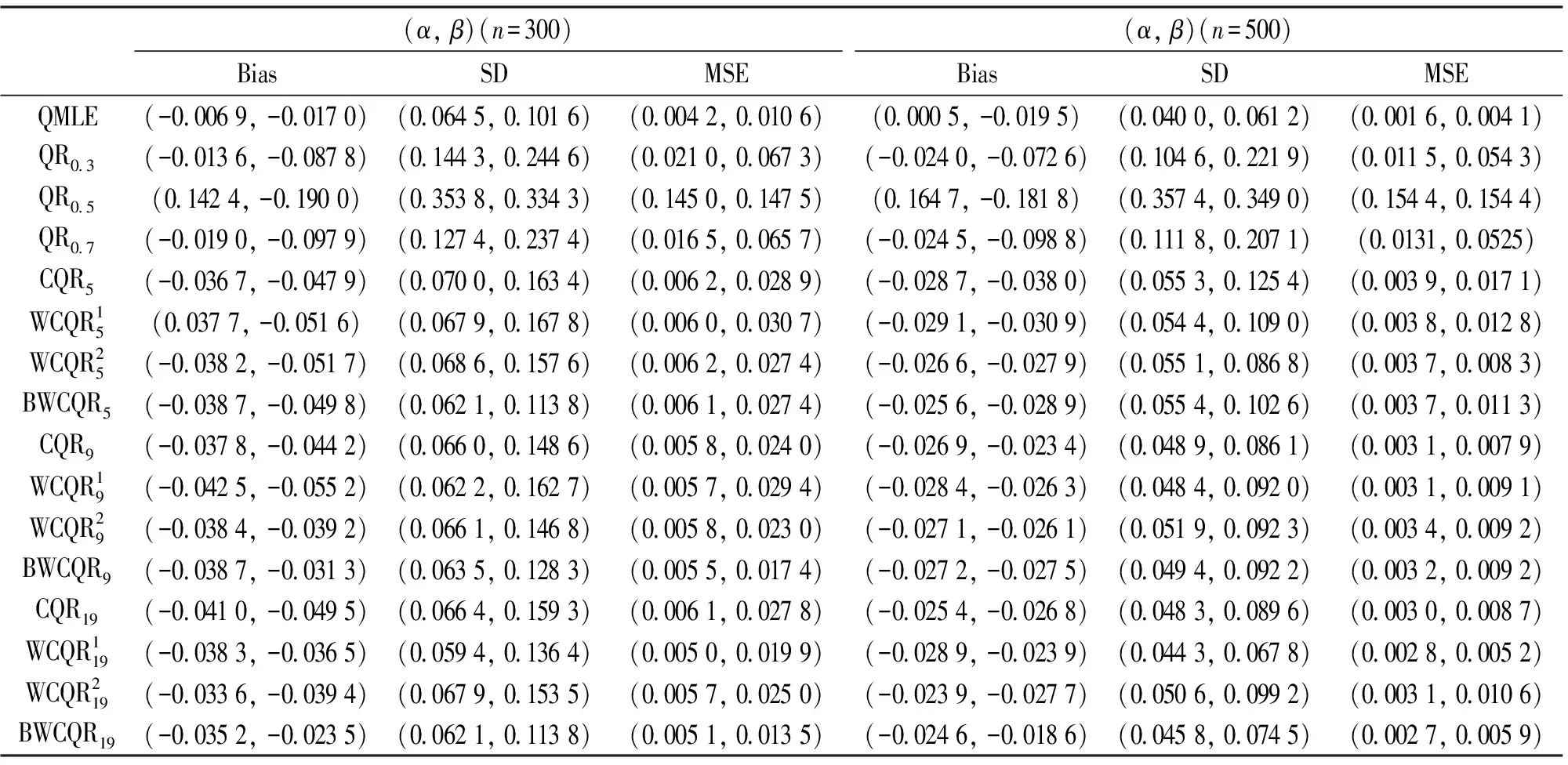
表1 GARCH(1，1)模型的不同估計的比較，ηt～N(0， 1)

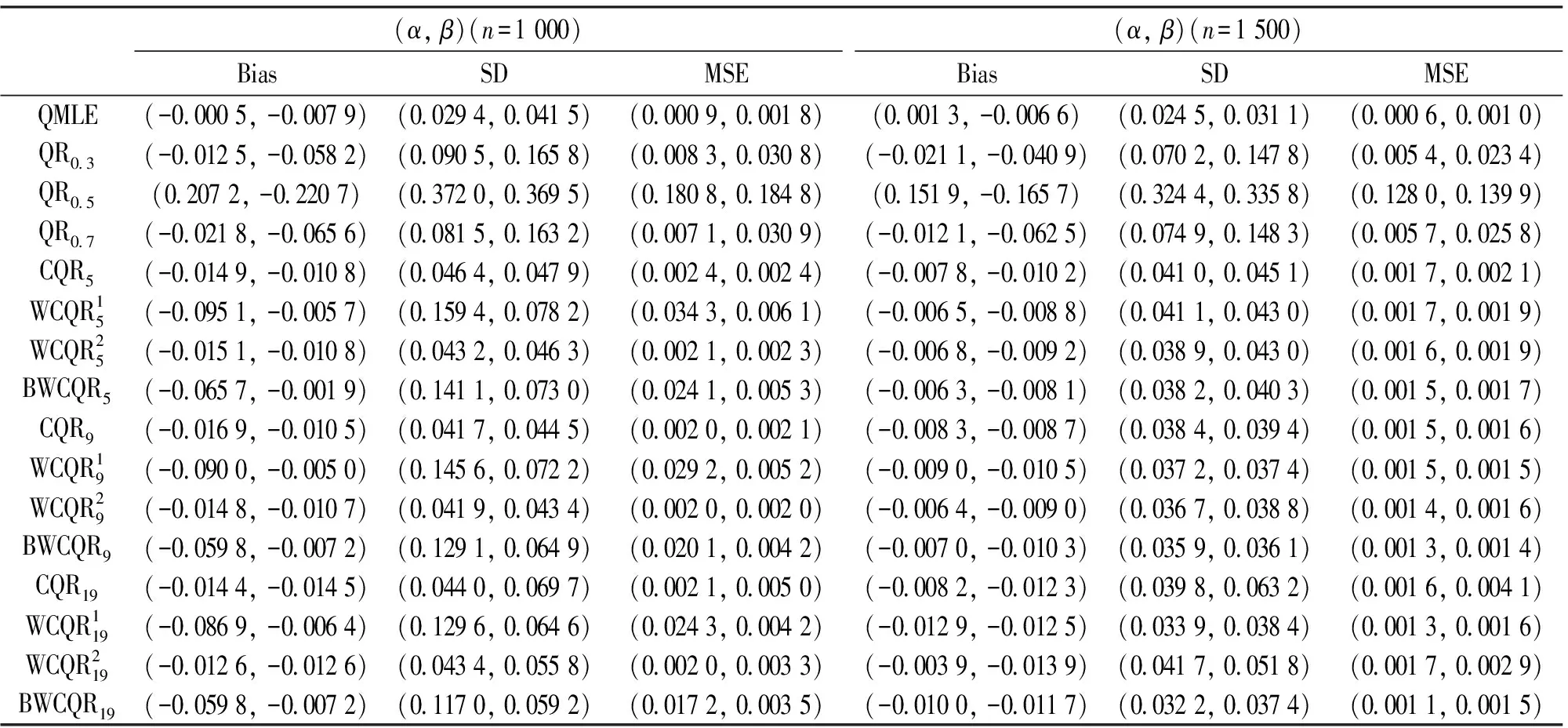
續表

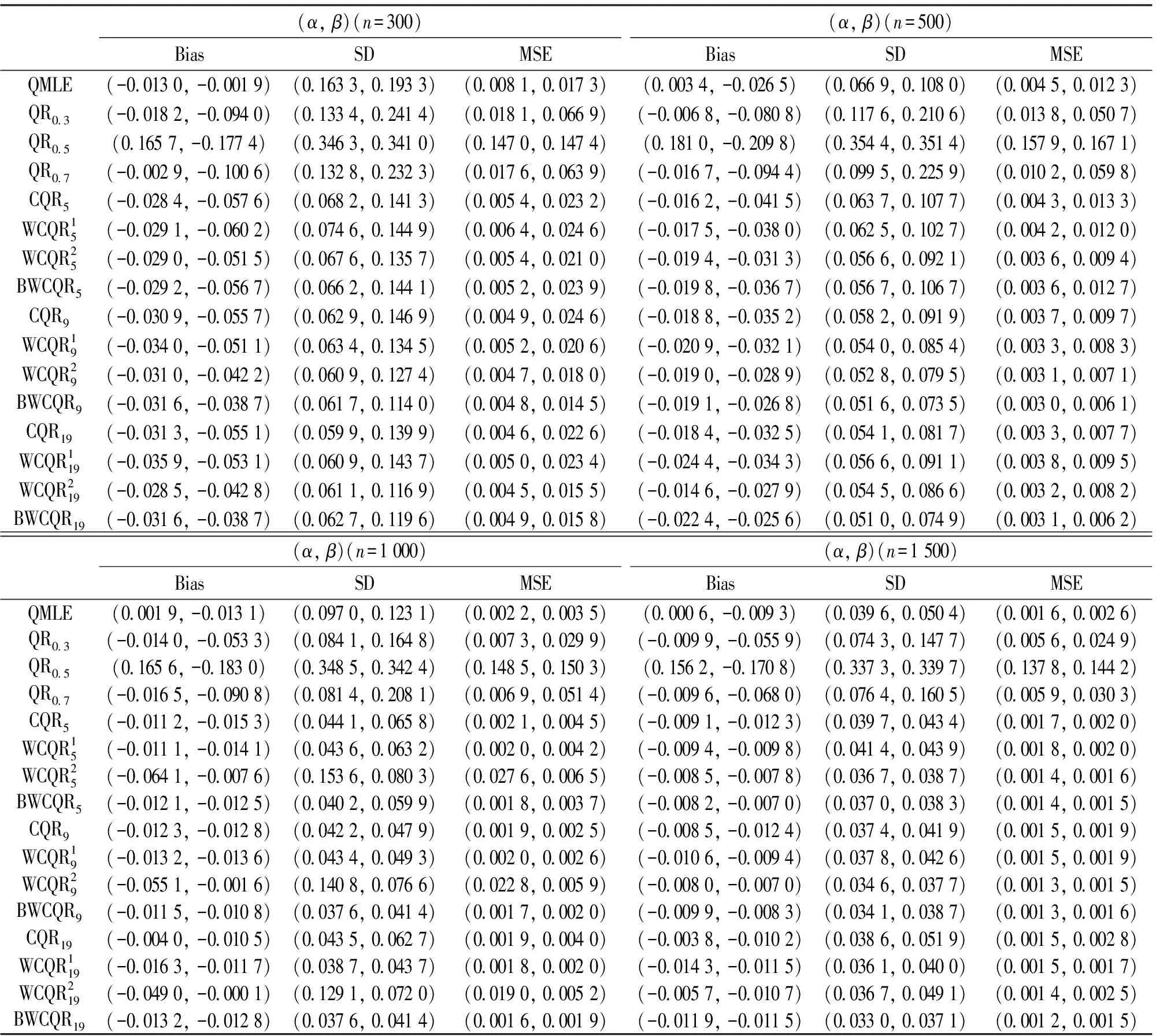
表2 GARCH(1，1)模型的不同估計的比較，ηt～t(5)

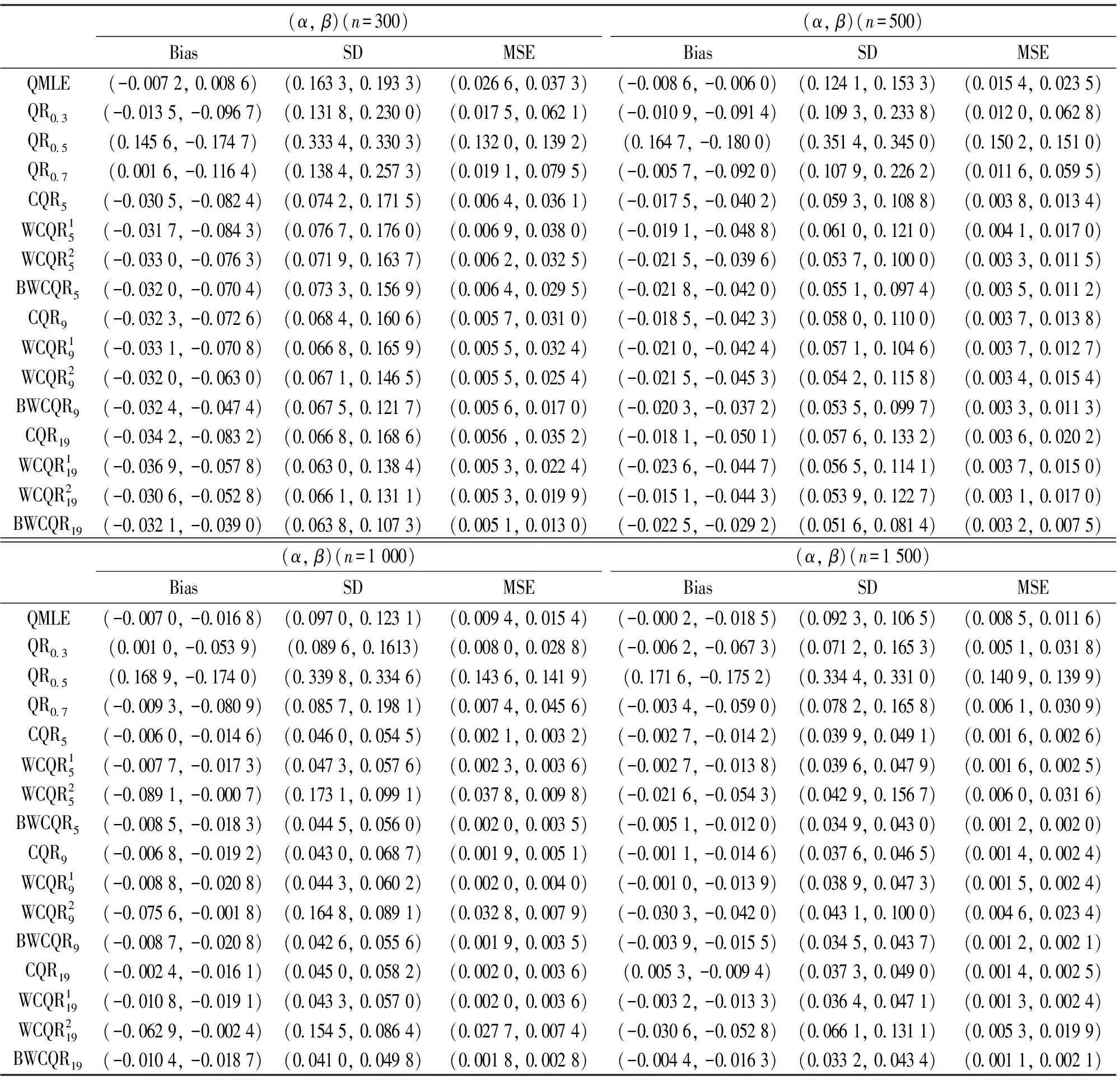
表3 GARCH(1，1)模型的不同估計的比較，ηt～t(3)

分析結果得到：

(i) 無論擾動序列的分布如何， 對任一估計， 隨著樣本量n的增大， MSE愈小；

(ii) 各類復合分位數估計對K值的敏感程度不強；

(iii) 樣本規模n一定時，K越大， MSE越小， 也即K取19時各類復合分位數回歸估計最優；

(iv) 當擾動項服從正態分布時， QMLE最優；

(v) 當擾動項服從重尾分布時， 總體而言， BWCQR估計明顯優于WCQR1， 略優于WCQR2， 且隨著K的增加BWCQR估計的競爭力愈強．

2.2 實證分析

選取上證和滬深300股指作為研究對象， 實證區間為2015年1月5日至2021年5月11日， 共計1 544個樣本數據． 記pt為第t交易日的收盤價，rt為百倍對數收益率：rt=100×(lnpt-lnpt-1)．

表4給出rt序列的描述性統計分析值． 均值大于0， 說明股指整體趨勢上行， 且序列不服從正態分布、 不獨立同分布． 綜上所述， 足以表明rt序列具有典型的高峰厚尾特征． Ljung-Box檢驗Q統計量和ADF檢驗表明序列具有明顯的長記憶性且平穩．

表4 股指收益率序列描述性統計信息

本文選用GARCH(1， 1)對該時間序列進行建模分析， 采用向前一步滾動窗口預測方法， 并將2015年1月5日至2020年1月23日作為初始滾動窗口． 本文對rt分別采用QMLE， MLE-t和BWCQR19進行擬合， 對應標準化殘差序列的ARCH-LM檢驗通過率列于表5． 表5結果符合數值模擬結論， BWCQR估計明顯優于QMLE和MLE-t．

表5 標準化殘差序列的ARCH-LM檢驗通過率

進一步， 上證指數全序列和滬深300股指全序列在BWCQR估計下的標準化殘差序列的自相關(ACF)圖和偏自相關(PACF)圖， 如圖1，2所示， 可見BWCQR估計下股指的標準化殘差序列是白噪聲序列， 這再次驗證了BWCQR估計的優良性．

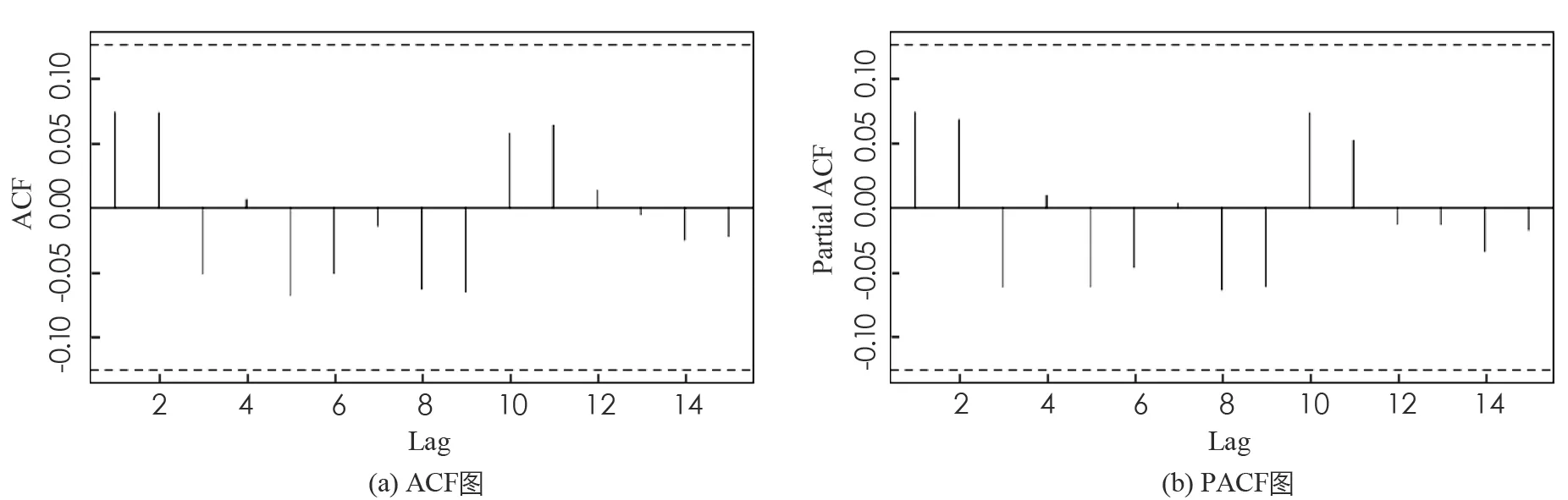
圖1 BWCQR估計下上證股指標準化殘差序列

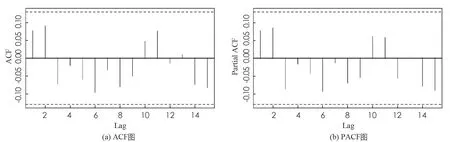
圖2 BWCQR估計下滬深股指標準化殘差序列

3 結語

本文提出了GARCH模型的BWCQR估計并探究其大樣本性質． 數值模擬結果顯示： 當擾動項序列服從正態分布時， QML估計略優于BWCQR估計； 當擾動項序列服從厚尾分布時， BWCQR估計明顯優于傳統估計． 我們將提出的BWCQR擬合分析上證和滬深股指波動系統， 結果表明BWCQR估計能更為合理有效地刻畫股指時序的波動規律．