一個種群與環境資源相互作用模型的有限差分逼近①

王文靜， 靳歡歡， 黃啟華

西南大學 數學與統計學院， 重慶 400715

從環境和自然發展的角度來看， 研究種群和自然資源之間相互依賴的關系是很有意義的． 許多科研工作者建立并研究了一系列描述種群與資源相互作用的數學模型， 例如： 文獻[1-2]研究了微生物在培養皿中對單一營養物質競爭的數學理論； 文獻[3-7]建立并研究了恒化器中兩個物種競爭同一種資源的競爭模型． 值得注意的是， 上述模型都是由常微分方程組給出， 其中包含的種群的所有個體被假定是相同的． 然而， 現實中同一種群的不同個體由于年齡、 大小等方面的差異會導致不同個體之間存在不同的出生率、 增長率、 死亡率[8-12]， 而且不同個體消耗資源的能力以及受資源影響的程度也可能是不同的． 因此在本文中， 我們建立并研究一個大小結構的種群和資源相互作用的數學模型．

(1)

其中c(x)是攝取率，H是半飽和常數． 模型的第三個方程為對應于第一個方程的邊界條件， 描述了種群在資源影響下的出生過程， 其中函數β是資源為R時， 大小為x的個體的繁殖率． 在模型的最后兩個等式中，u0(x)是初始種群密度，R0是資源的初始值．

1 弱解和有限差分

設D=[xmin，xmax]×[0， ∞)， 并且c是足夠大的正常數． 假設模型(1)中的參數滿足下面條件：

(A5)u0∈BV[xmin，xmax]且u0(x)≥0．

(A6)R0∈BV[xmin，xmax]且R0(x)≥0．

仿照文獻[13]， 將模型(1)中的第一個方程乘φ(x，t)， 再通過分部積分并利用初始條件和邊界條件， 定義模型(1)的弱解如下：

定義2一個函數u∈IBV([xmin，xmax]×[0，T])， 如果滿足以下條件就稱為模型(1)的弱解：

其中φ∈C1((xmin，xmax)×(0，T))．

定義差分算子

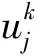
使用隱式有限差分格式， 對系統進行如下的離散化：

(2)

初始條件為

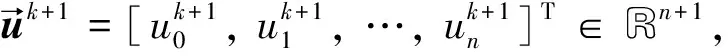
(3)

(4)

引理1假設Δt選擇得足夠小， 使得2cΔt≤1． 那么線性系統(3)，(4)有唯一的非負解．

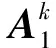
2 有限差分逼近的估計

首先證明差分逼近在l1空間的范數是有界的．

引理2假設引理1成立， 則存在一個正常數B1， 使得‖uk‖1+|Rk|≤B1．

證將(2)式的第一個等式左右兩邊乘Δx， 并將j=1，…，n對應的各式相加， 有

(5)

用類似的方式處理(2)式的第二個等式， 有

Rk+1(1+cΔt)≤Rk+hΔt

(6)

現在令Sk=‖uk‖1+|Rk|并且將(5)式和(6)式相加， 有

再證明差分逼近在l∞空間的范數是有界的．

引理3假設引理1成立， 則存在一個正常數B2， 使得‖uk‖∞≤B2．

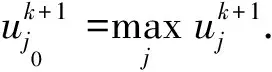
(7)

如果1 ≤j0≤n， 則利用(2)式的第一個等式， 可得

(8)

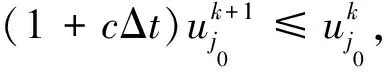
(9)

根據(7)-(9)式， 我們有

因此存在正常數B2， 使得‖uk+1‖∞≤B2．

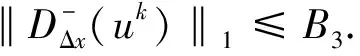
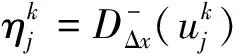
(10)

另一方面， 如果j=1， 那么

因此， 由(2)式的第一個等式有

(11)

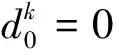
將j=1，2，…，n對應的各式相加， 得到

(12)

容易得到

(13)

由不等式(12)和(13)， 得到

另外， 注意到

(14)

其中α在R(tk)和R(tk-1)之間， 而且

(15)

由(14)，(15)式有

(16)

其中ξ在R(tk)和R(tk-1)之間， 且存在正常數B4和B5， 使該不等式成立， 則該定理得證．

下一個結果表明， 差分逼近滿足關于t的李普希茨條件．

引理5假設引理1成立． 則存在一個正常數A>0， 使得對任何r>q有

(17)

證將(2)式的第一式的所有j相加并乘Δx， 得到

因此，

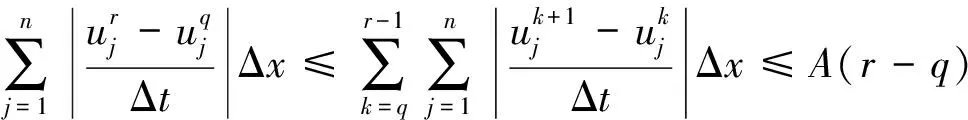
可類似證明引理5的第二個不等式．

3 有限差分的收斂性和弱解的存在唯一性

定義如下的函數族{UΔx， Δt}， {RΔt}

其中x∈[xj-1，xj)，t∈[tk-1，tk)，j=1，…，n，k=1，…，l． 且由引理2-5， 函數集合{UΔx， Δt}， {RΔt}在拓撲空間L1(xmin，xmax)×(0，T)和C(0，T)中是緊的， 并且由文獻[15]中的引理16.7的證明． 以下結果成立．

(18)

以及

并且存在一個常數Γ使得極限函數滿足

‖U‖IBV([xmin， xmax]×[0， T])≤Γ， ‖R‖C[0， T]≤Γ

接下來證明通過上述差分格式構造的極限函數u(x，t)與R(t)實際上是模型(1)的弱解．

定理2定理1定義的極限函數u(x，t)與R(t)是模型(1)的弱解并且滿足

‖u(·，t)‖1+|R(t)|≤B1

以及

‖u‖L∞([xmin， xmax]×[0， T])+‖R‖C[0， T]≤B1+B2

證使用類似于文獻[15]的引理16.7中的證明方法可得結論成立．

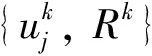
這里

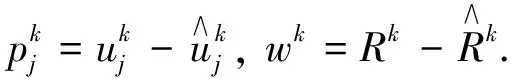
(19)

得到

(20)

(21)

將(20)式和(21)式同時乘Δt， 并將所得的不等式相加， 得到

其中c5=max{c1+c4，c3}， 結論得證．

接下來證明定理1和定理2中定義的解是唯一的．

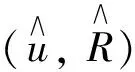
(22)

成立， 則表明模型(1)的弱解是唯一的．

(23)

有唯一解． 再用這個解考慮下面的初邊值問題：

(24)

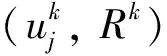
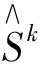
(25)

由定理1可以求不等式(25)右側式子的極限

(26)

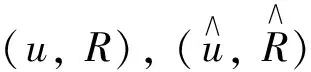
(27)

在定理1中有定義． 由Gronwall不等式， 得到(22)式．