帶有終端約束的線性二次最優控制問題①
常紹敏, 丁翊珊, 邱潔, 王燕青
西南大學 數學與統計學院, 重慶 400715
經過半個多世紀的發展, 線性二次最優控制問題(LQ問題)被廣泛研究[1-2]. 但是, 已有的結果大多是系統的狀態和控制都不帶有任何約束, 同時現有的算法的收斂速度也鮮有涉及. 近期, 文獻[3]考慮了帶終端約束的隨機系統的LQ問題, 研究了該問題的可解性問題. 本文是在文獻[3-4]的基礎上研究一類帶有終端約束的確定系統的LQ問題, 并給出了數值計算方法, 最后通過具體例子驗證了數值方法的有效性.
1 預備知識
本文考慮以下狀態方程:
(1)
性能指標為

其中:T>0,A∈Rn×n,B∈Rn×m,Q∈Rn×n,R∈Rm×m.
經典的LQ問題為: 對于受控系統(1), 在平方可積的控制函數空間中, 尋找最優控制, 極小化二次性能指標J(·). 但在實際問題中, 控制函數通常帶有一定的約束. 本文中考慮使得系統狀態達到特定目標的控制集, 即狀態帶有終端約束的LQ問題. 對于狀態的預期目標xT∈Rn, 定義控制函數類
U∶= {u(·)∈L2(0,T; Rm)|x(T;x0,u(·))=xT}
帶終端約束的LQ問題(簡記為CLQ問題)描述如下:
對于給定的x0,xT∈Rn, 尋找控制u*(·)∈U, 使得
(2)
如果滿足(2)式的u*(·)存在, 則其被稱為CLQ問題的最優控制, 相應的狀態x*(·)∶=x(·;x0,u*(·))被稱為最優狀態, (x*(·),u*(·))被稱為最優對. 上述問題稱為帶有終端約束的線性二次最優控制問題(簡稱為CLQ問題).
為了保證控制集U的非空性和CLQ問題的可解性, 我們在本工作中作如下假設:
(A) 系統(1)在區間[0,T]上精確能控, 即Rank(B,AB, …,An-1B)=n;Q為半正定矩陣,R為正定矩陣.
引理1系統(1)在[0,T]上精確能控的充要條件為系統(1)的Gram矩陣Ψ(0,T)可逆, 其中

Φ(·)滿足
2 主要定理
采用拉格朗日乘子法, 我們首先將CLQ問題轉化為無約束的LQ問題. 引入拉格朗日泛函:
Jλ(u(·))=J(u(·))+2〈λ,x(T)〉
其中x(T): =x(T;x0,u(·))為系統(1)的狀態在t=T處的值. 對于給定的λ, 無約束的LQ問題即(LQ)λ問題為:
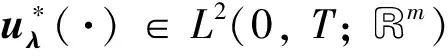
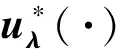
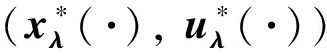
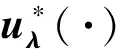
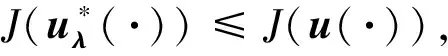
利用引理2, 求解CLQ問題的最優控制, 就可以轉化為求解如下兩個子問題:
(1) (LQ)λ問題的最優控制問題;
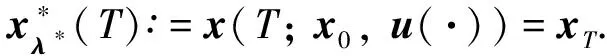
對于(LQ)λ問題的可解性, 有如下定理.
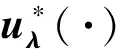
(4)
證(LQ)λ問題唯一可解性可以用文獻[1]第七章定理2.1的方法得到. 現在證明定理的剩余部分.
我們記
由ε的任意性, 可得
(5)
另一方面, 由方程組(4)容易得到
兩邊積分, 從而
(6)
由(5)式和(6)式可得
又由u(·)的任意性, 得到
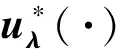
定理1給出了最優控制的開環表示, 而在應用中, 人們更希望給出閉環表示, 即狀態反饋形式. 接下來, 我們就研究CLQ問題的閉環表示. 我們引入Riccati方程:
(7)
和兩個常微分方程(簡稱ODE):
(8)
(9)
關于方程(7),(8),(9)的適定性, 讀者可以參考文獻[1,5].
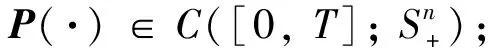
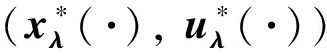
其中φ(·),yλ(·)分別是方程(8),(9)的解.
證設x(·)是如下ODE的解
(10)
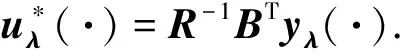
(11)
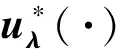
利用方程(7)-(9), 我們可以得到
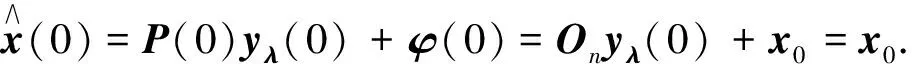
下面引入輔助系統
(12)
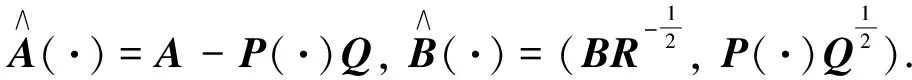
引理4系統(12)在[0,T]上精確能控的充要條件是系統(1)在[0,T]上精確能控.
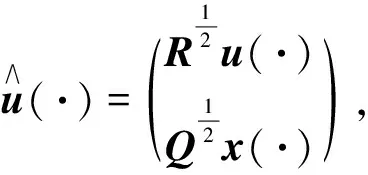
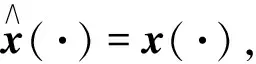
通過引入
引理5P(T)是正定矩陣.
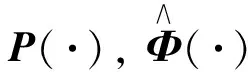
進一步對兩邊在[0,T]上積分, 有
從而
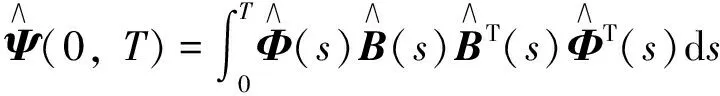
現在我們可以綜合前面的結果, 得到CLQ問題的可解性.
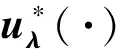

3 最優控制的計算方法
根據定理3, 可以得到CLQ問題的基于狀態反饋的最優對的計算方法. 具體計算步驟如下:
1) 選取最優參數λ*.
①解得Riccati方程(7)和ODE(8)的解P(·),φ(·).
②求解最優參數λ*=P-1(T)(φ(T)-xT).
2) 解得最優參數λ*所對應ODE(9)的解yλ*(·).
現在, 我們通過一個具體的例子, 利用上述計算方法, 得到CLQ問題的最優對.
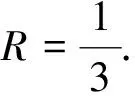
解: 將條件數據代入Riccati方程(7)得其精確解為
由ODE(8)解得
φ(t)=0
進而可以計算最優參數:
再由ODE(9)解得
最后可以計算最優對為
由例1可知, 即便對于1維系統, 要求解CLQ問題仍然十分復雜, 這就促使我們研究上述計算方法的數值算法. 接下來我們上述的計算方法給出數值計算的版本, 首先將時間區間[0,T]均分為N份, 即有
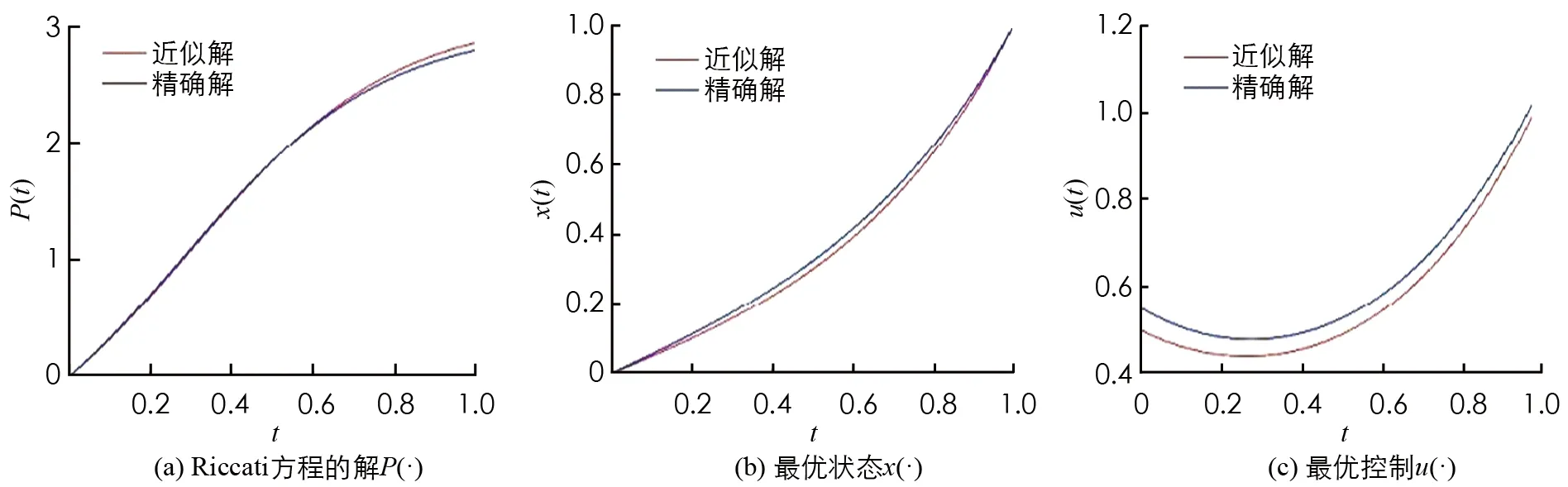
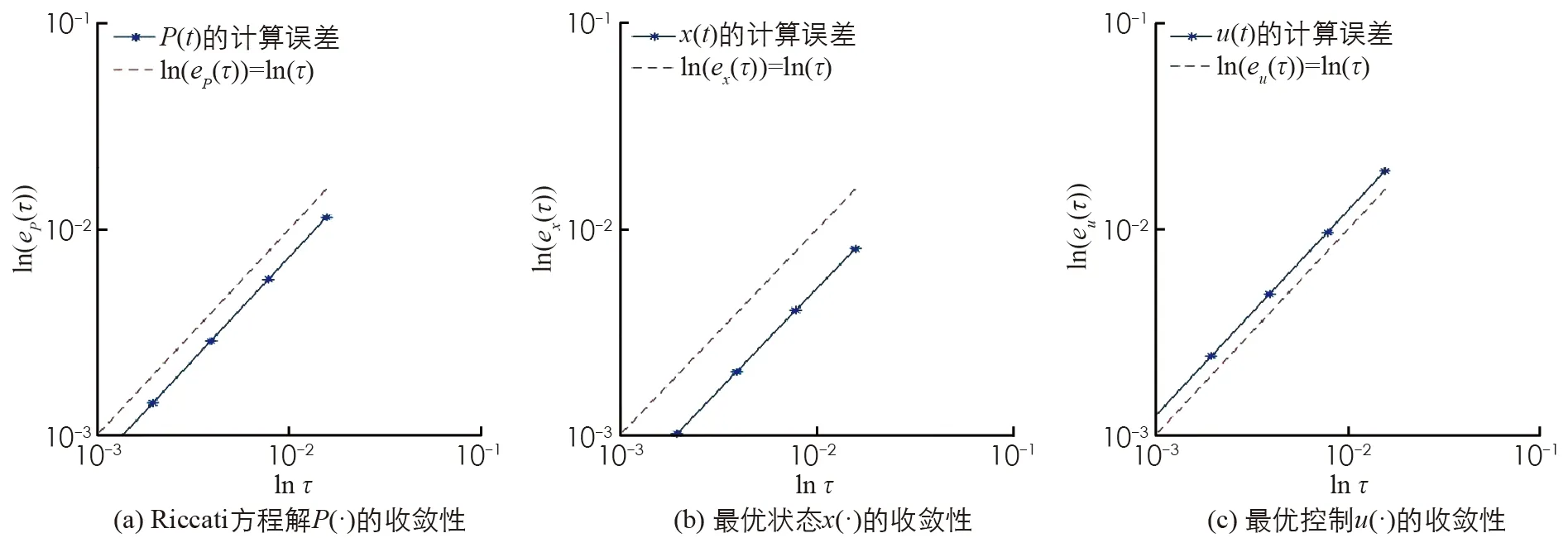
0=t0 CLQ問題數值算法: Λ=diag{μ1,μ2, …,μm0, 0, …, 0},μi>0,i=1,2,…,m0 定義 2) 選取最優參數λ*的近似值λ. ①求解Riccati方程(7)如下: 采用Euler方法求解ODE(8), 得到其數值解φi,i=0,1,…,N. ②求解近似最優參數λ 3) 利用Euler方法求解近似最優參數λ所對應ODE(9), 得到其數值解yi,i=0,1,…,N. 4) 求解近似最優對(xi,ui),i=0,1,…,N: xi=Piyi+φi,ui=R-1BTyi 取N=25, 用數值算法得到例1的數值解, 和精確解的比較見圖1. 圖1 精確解與離散方程解的對比 圖2 Riccati方程與最優對離散化計算方法的收斂性 本文利用參數選擇的方法對帶有終端約束的LQ問題給出了可解性的理論結果, 同時基于最優控制的閉環表示給出了計算最優對的數值算法. 與基于開環表示的確定/隨機系統的LQ問題算法相比, 本文算法的優勢在于: 避免了條件數學期望的計算, 避免使用梯度下降法等算法[6-10], 從而大大減少了計算量.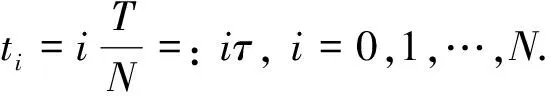
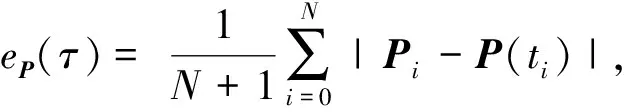
4 結論

