基于均值零化算子的灰色絕對關聯度模型的改進及其應用①

羅丹， 王松華

百色學院 數學與統計學院， 廣西 百色 533000

上世紀80年代鄧聚龍教授提出灰色關聯分析理論[1]， 隨后這一理論得到了極大的發展與應用[2-15]． 后1991年文獻[2]根據鄧氏灰色關聯分析模型[3]研究了一類廣義灰色關聯分析模型， 首次提出了絕對關聯分析模型． 該模型有效解決了許多科研、 生產中的實際問題， 一直以來受到研究者的廣泛關注． 在文獻[2]提出的灰色絕對關聯分析模型中， 灰色關聯算子起到了重要的作用． 但考慮到絕對關聯度分析模型在做實際問題的定量分析時， 存在因自然災害、 戰爭、 疫情等意外因素的影響引起系統行為序列數據受到沖擊干擾而失真的問題， 本文采用均值化算子構造方法提出一種均值化的新關聯算子并對灰色絕對關聯度模型進行改進， 并討論該改進模型的性質和應用．

1 新的灰色關聯算子的構造

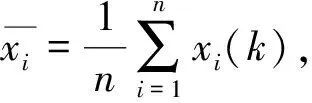
定義2設系統行為序列Xi={xi(1)，xi(2)， …，xi(n)}，D為序列算子且

XiD={xi(1)d，xi(2)d， …，xi(n)d}

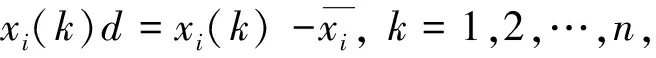
2 改進的灰色絕對關聯度模型及其性質

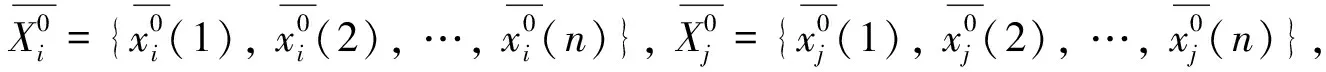
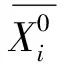
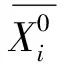
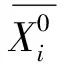
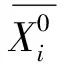
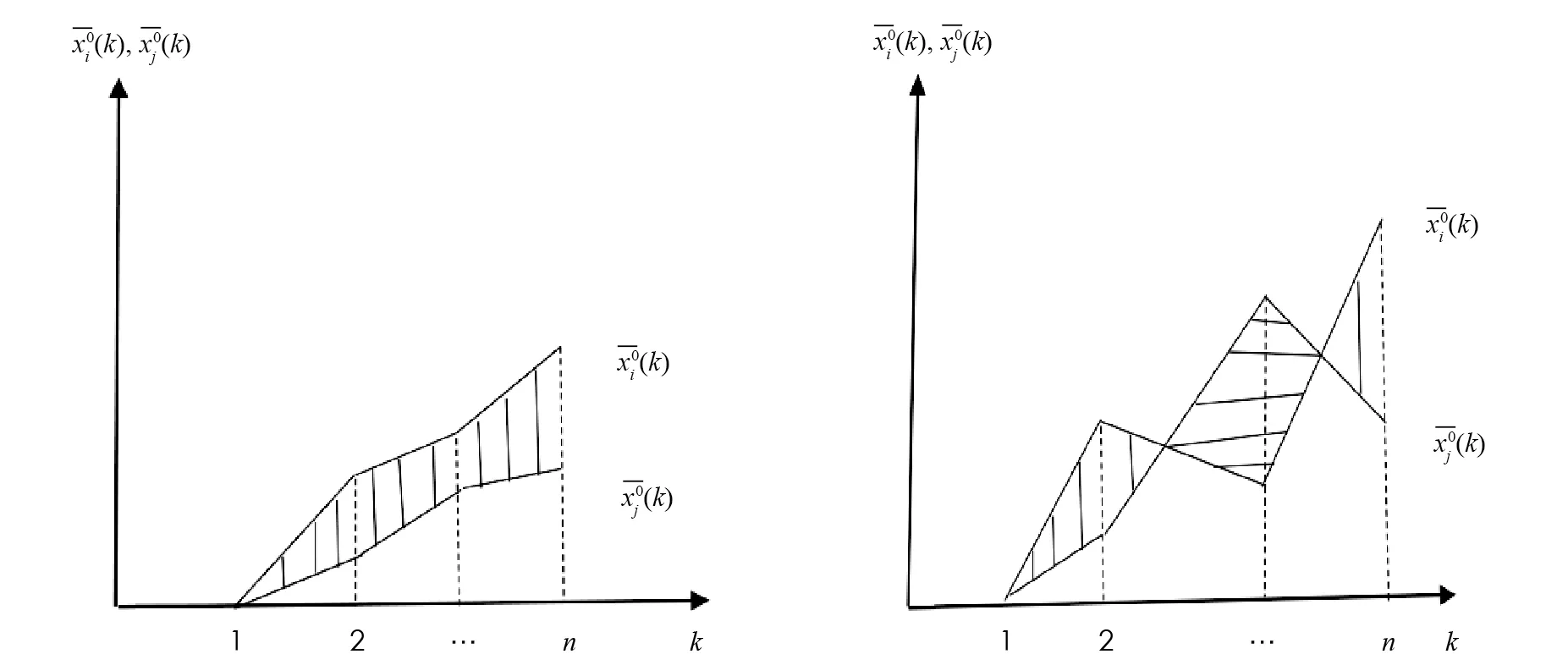
恒在的上方與相交

定理2廣義灰色均值關聯度

滿足灰色關聯公理中規范性、 偶對稱性與接近性．

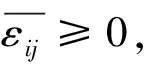
3) 接近性： 顯然成立．

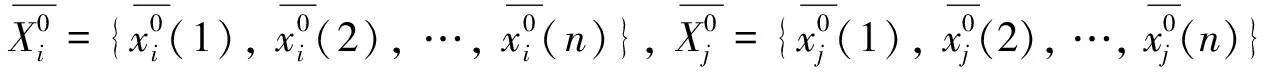
定理3設Xi與Xj的長度、 時距相同且皆為等時距序列， 則

證不妨設Xi與Xj皆為1時距序列， 由引理1和定義1得

3 實例分析

例1由文獻[4]， 設有如下數據序列：

其中：X1為參考序列，X2與X3為相關因素序列． 計算得到的關聯度及其關聯序見表1， 數據序列折線圖見圖2．

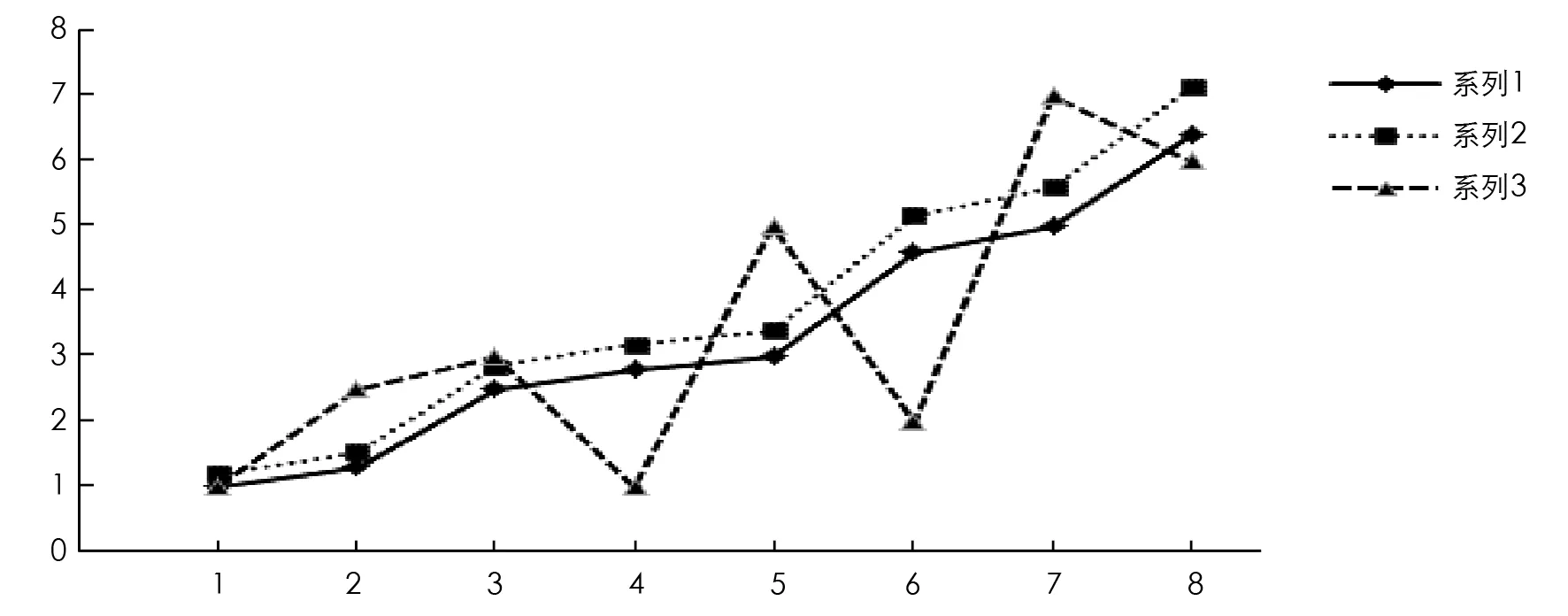
圖2 例1數據序列折線圖

表1 關聯度與關聯序

由圖2可以看出， 序列X1和X2的發展趨勢更接近， 而序列X1和X3的發展趨勢差異較大， 即ε13<ε12． 所以， 本文構造的灰色關聯度如實地反映了數據序列發展態勢的相似程度．

例2引用文獻[5]數據(表2)對我國海洋漁業經濟增長與其影響因素的關系進行研究．

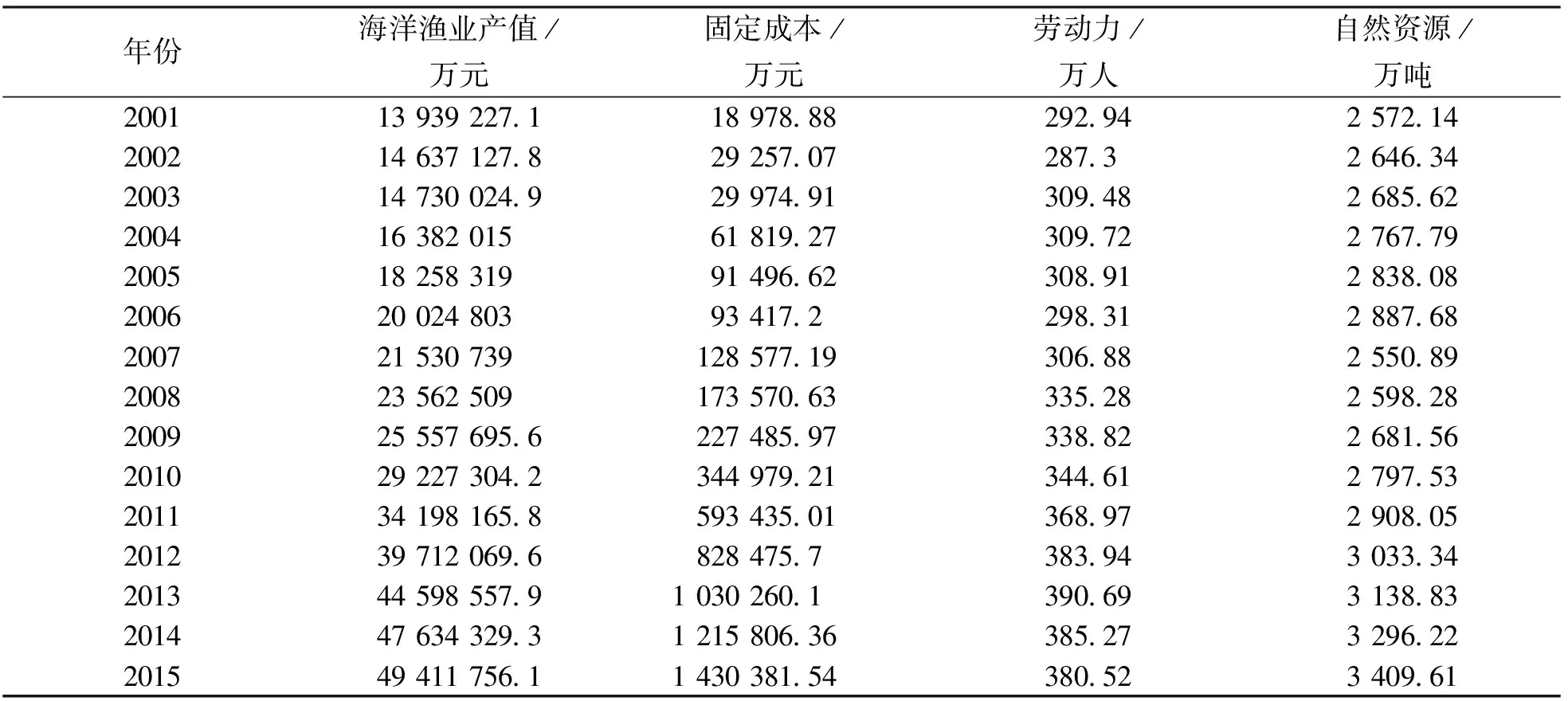
表2 2001-2015 年我國海洋漁業數據

將中國海洋漁業產值作為系統行為的參考序列X0(t)， 把固定成本、 勞動力、 自然資源看作X1(k)，X2(k)，X3(k)，k=2001，2007，…，2015.利用本文算子構造的灰色關聯模型計算步驟及結果如下：

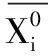
表3 均值零化像計算結果表

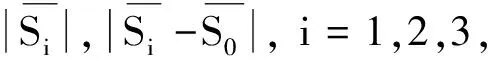
3) 由新構造的灰色均值關聯度計算公式

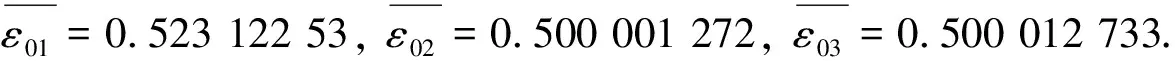
本文構造的新的灰色均值關聯度模型計算結果跟實際情況相符合， 具有一定的實用性和可靠性．

4 結論

針對在利用灰色絕對關聯度分析模型做實際問題的定量分析時， 存在因自然災害、 戰爭、 疫情等意外因素的影響， 引起系統行為序列數據受到沖擊干擾而失真的問題， 文章根據廣義灰色絕對關聯分析模型基本思想， 采用均值化算子構造方法， 提出一種名為均值零化的新關聯算子并對灰色絕對關聯度模型進行改進． 改進的灰色絕對關聯度模型具有規范性、 偶對稱性、 接近性等性質． 初步的數值實例表明， 改進的灰色關聯度模型能真實地反映序列曲線的關聯程度， 所得關聯分析結果較為客觀可靠， 新的灰色均值關聯度模型算法簡單且易于在計算機上實現， 具有一定的實用參考價值， 從而進一步拓寬了廣義灰色關聯度模型的應用領域．