對流環境下具有混合遷移模式的捕食者_食餌模型分析①
張柏楓, 張國洪
西南大學 數學與統計學院, 重慶 400715
捕食者-食餌系統是自然界普遍存在的一種生態系統. 各種不同的捕食者-食餌動力學模型已經被提出來研究兩個種群之間的相互關系[1]. 特別地, 受亞得里亞海各種魚類種群統計研究的啟發, 文獻[2]提出了如下捕食者-食餌模型
(1)
其中:u和v分別表示食餌和捕食者的密度;r1為食餌的增長率;a和c表示捕食行為導致的種間相互作用;r2為正數時, 表示捕食者的增長率, 捕食者除食餌外還有其他的食物來源,r2為負數時, 表示捕食者的死亡率, 捕食者只依賴于食餌存活. 文獻[3]給出了模型(1)的全局動力學性態, 發現當共存平衡解存在時, 則必然全局穩定. 考慮到種群的空間異質分布, 文獻[4]在上述模型的基礎上研究了考慮種群隨機擴散條件下的反應擴散捕食者-食餌模型, 發現其動力學行為和對應的ODE模型(1)類似. 然而除了隨機擴散外, 許多物種還可能向某個方向定向遷移, 如捕食者主動向食餌方向運動以追擊獵物等, 該類行為被稱為趨餌性[5]; 同時, 在某些環境中種群也可能被動地進行定向運動, 例如在河流生態系統中被單向流動的水流推動. 近年來對流(如河流)環境下的單種群模型, 兩種群相互競爭模型的研究已成熱點, 研究表明對流的引入對系統的動力學行為有重要影響[6-8]. 為了研究對流環境對捕食者-食餌系統動力學行為的影響, 本文在模型(1)的基礎上考慮如下反應擴散對流模型
(2)
其中:u和v分別表示食餌和捕食者的密度;l是棲息地的長度; 參數d1,d2為相應的擴散速度,q為對流速度, 均為正常數;u0(x)和v0(x)分別表示食餌和捕食者的初始分布. 我們只考慮r2為捕食者的增長率的情況, 其他參數的意義與模型(1)中的相同. 假設捕食者只做隨機擴散, 而食餌除隨機擴散外還會朝某一個方向遷移. 這種現象在生態學中是可能存在的, 例如捕食者是雜食性陸地動物并且傍河而居, 而食餌是河流生物, 或者在河流生態系統中, 捕食者常居于流速為零的區域(河底)而食餌常居于流速不為零的區域(河面). 由于捕食者只做隨機擴散, 所以邊界條件vx(0)=vx(l)=0表示沒有任何捕食者可以通過棲息地的邊界. 對于食餌的邊界條件,d1ux(0)-qu(0)=0表示對流環境上游不允許食餌通過,d1ux(l)-qu(l)=-bqu(l)表示對流環境下游食餌的損失與對流速度相關, 其中b≥0是衡量對流作用導致食餌在下游產生損失數量的測度, 詳細的推導和生物意義可以參考文獻[9].
1 系統的耗散性
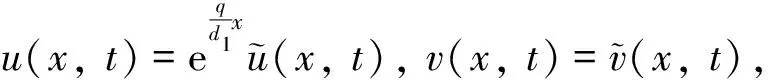
(3)
易知系統(2)和系統(3)的解結構相同. 不失一般性, 我們假設l=1.
首先考慮單物種系統
(4)
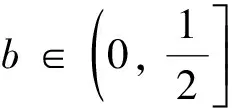
引理1設d,q,r>0且b≥0. 關于系統(4)有如下結論:
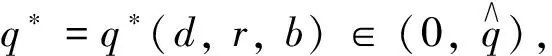
(ii) 若b=0, 則系統(4)存在唯一的正穩態解θ(d,q,r), 并且是全局穩定的.
引理2設d,q,r>0且b≥0. 若系統(4)的正穩態解θ(d,q,r,b)存在, 則θ(d,q,r,b)≤r.
證首先θ(d,q,r,b)滿足如下方程
(5)
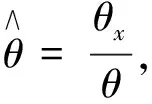
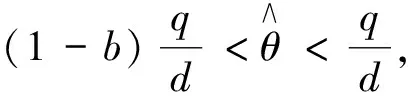

顯然, 總存在x1∈[0, 1], 使得θ(x1)=r, 并且當x∈[x1, 1]時, 總有θ(d,q,r,b)≥r. 將(5)式的第一個式子在[x1, 1]上積分, 得
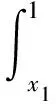

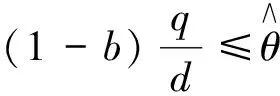
定理1設d1,d2,r1,r2>0且b≥0. 系統(2)存在唯一的正解(u,v), 并且正解最終有界.
證首先, 根據文獻[11], 系統(3)的解局部存在且唯一, 則系統(2)的解也局部存在且唯一. 其次, 由最大值原理, 易知u>0,v>0. 故只需證明解的有界性. 結合解的正性和系統(3)的第一個方程可得
(6)
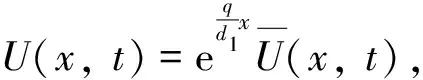
(7)
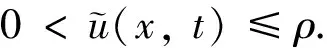
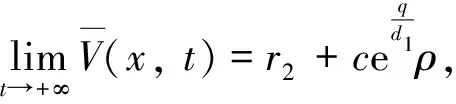
因為系統(2)和等價系統(3)的解結構相同, 所以系統(2)的解(u,v)最終有界. 證畢.
2 平衡點的穩定性
易見系統(2)可能存在3個邊界平衡態解(0, 0), (θ(d1,q,r1,b), 0)和(0,r2). 為了研究這些平衡解的穩定性, 我們首先證明如下結論.
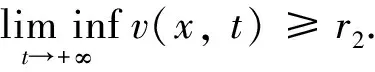
證由系統(2)的第二個方程有
vt≥d2vxx+v(r2-v), 0
定理2表明平衡點(0, 0)和(θ(d1,q,r1,b), 0)一定是不穩定的, 下面來討論(0,r2)的穩定性. 考察特征值問題
(8)
其中:d,q>0,b≥0且r∈R. 根據Krein-Rutman定理[15]知問題(8)存在主特征值λ1(d,q,r,b), 且對應的有嚴格正的特征函數φ1(d,q,r,b). 結合系統(4)中的設定, 根據文獻[6]的引理2.1,2.2和文獻[12]的命題3.1, 有下列結論成立.
引理3設d,q>0,b≥0且r∈R. 特征值問題(8)有如下性質:
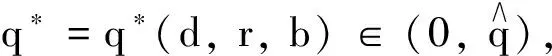
(ii) 若r≤0, 則λ1(d,q,r,b)≤0, 并且b=0時,λ1(d,q,r,0)=r.
定理3設d1,d2,r1,r2,q>0且b≥0. 平衡解(0,r2)的局部穩定性情況如下:
(H1) 當r1>ar2時, 若b>0, 則存在q*(d1,r1-ar2,b), 使得q∈(0,q*(d1,r1-ar2,b)), (0,r2)是不穩定的,q∈(q*(d1,r1-ar2,b), +∞), (0,r2)是局部漸進穩定的;
(H2) 當r1>ar2時, 若b=0, 則(0,r2)是不穩定的;
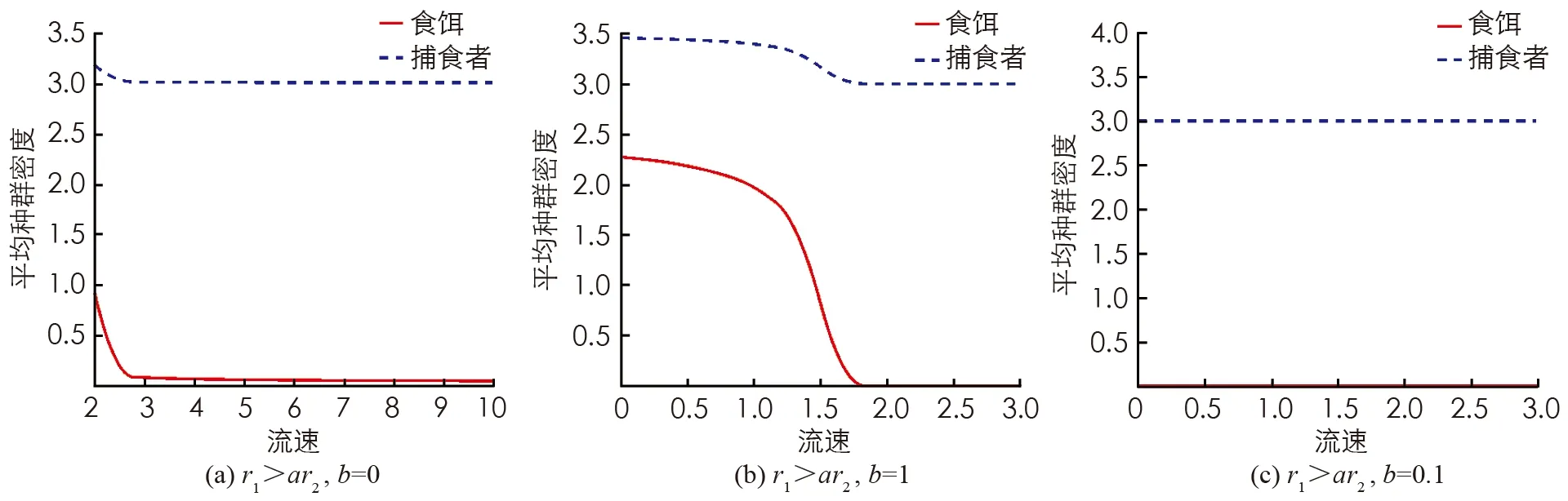
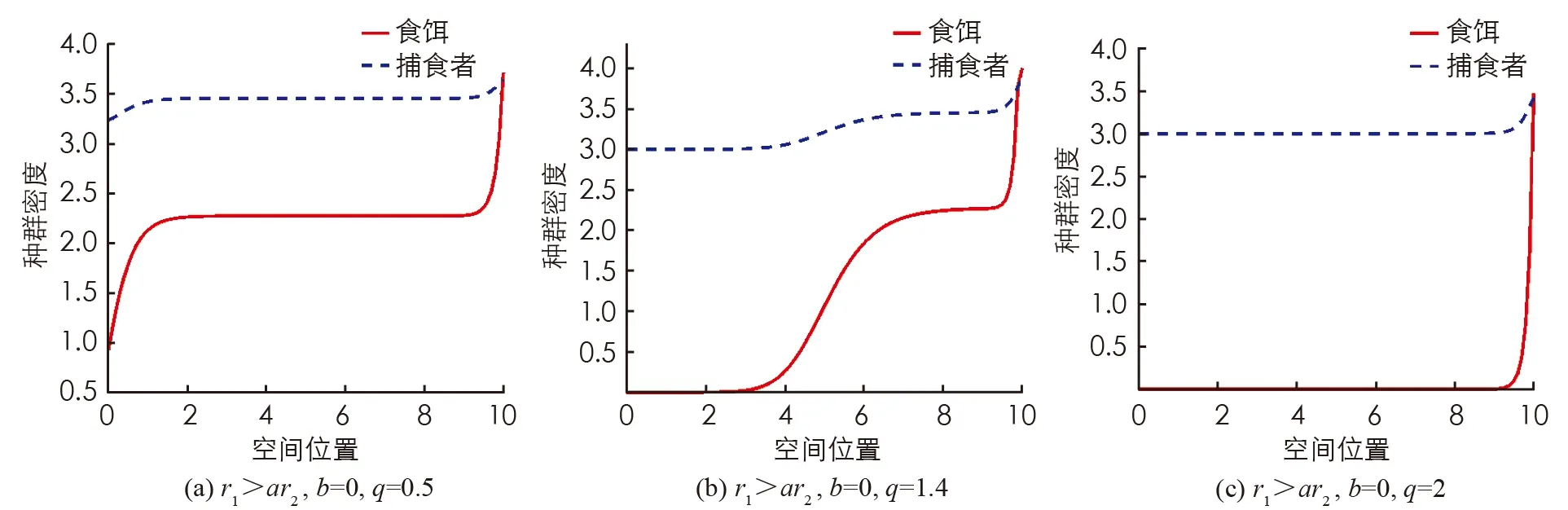
(H3) 當r1 證系統(2)在(0,r2)處線性化后的特征值問題如下 (9) 定義Λ為特征值問題(9)的譜, 顯然Λ=Λ{φ=0}∪Λ{φ≠0}. 當φ=0時, 考察特征值問題 (10) 可取特征函數ψ1(x)=1, 故主特征值λ1=-r2<0. 因此, 對屬于特征值問題(10)的特征值λ, 都有Reλ<λ1<0, 則sup{Reλ,λ∈Λ{φ=0}}<0. 當φ≠0時, 考察特征值問題 根據引理3, 當r1>ar2時, 若b>0, 則存在q*(d1,r1-ar2,b), 使得q∈(0,q*(d1,r1-ar2,b)),λ1(d1,q,r1-ar2,b)>0, 則 sup{Reλ,λ∈Λ{φ=0}∪Λ{φ≠0}}>0 所以(0,r2)是不穩定的,q∈(q*(d1,r1-ar2,b), +∞),λ1(d1,q,r1-ar2,b)<0, 則 sup{Reλ,λ∈Λ{φ=0}∪Λ{φ≠0}}<0 所以(0,r2)是局部漸進穩定的, (H1)成立. 類似地, 當r1>ar2時, 若b=0, 由引理3, 可知λ1(d1,q,r1-ar2,b)=r1-ar2>0, (0,r2)是不穩定的, (H2)成立. 當r1 由定理3可知(0,r2)的局部穩定性, 下面證明若(0,r2)是局部穩定的, 則(0,r2)是全局吸引的, 從而(0,r2)也是全局穩定的. 定理4設d1,d2,r1,r2,q>0且b≥0. 若條件 (C1)r1 (C2)r1>ar2,b>0,q∈(q*(d1,r1-ar2,b), +∞). 之一成立, 則平衡解(0,r2)是全局穩定的. 證由定理2有 (11) 現考慮如下方程 (12) 當(C1)成立時, 取ε足夠小, 使得r1+aε-ar2<0, 再由引理3得λ1(d1,q,r1+aε-ar2,b)<0. 根據文獻[10], 系統(12)的解U=0是全局穩定的當且僅當λ1(d1,q,r1+aε-ar2,b)<0, 則 當(C2)成立時, 有r1+aε-ar2>r1-ar2>0, 由引理1可知存在q*(d1,r1+aε-ar2,b), 使得當q∈[q*(d1,r1+aε-ar2,b), +∞)時, 系統(12)的解U=0是全局穩定. 又因為(C2)成立時, 有q∈(q*(d1,r1-ar2,b), +∞), 并且ε是任意小的正常數, 所以必有q∈[q*(d1,r1+aε-ar2,b), +∞), 故 由比較原理易得 (13) 再結合(11)式和(13)式, 有 可知(0,r2)是全局吸引的, 又因(0,r2)的局部穩定性已知, 所以結論成立. 在這一節中, 我們使用一致持續性理論來研究系統(2)的一致持續性條件, 相關理論的詳細介紹可以參考文獻[13]. 定理5設d1,d2,r1,r2,b>0且r1>ar2. 若q∈(0,q*(d1,r1-ar2,b)), 則系統(2)是一致持續的, 即存在一個正常數η, 使得 (14) (15) (16) (17) (18) WS((0, 0))∩D-1(0, +∞)=?,WS((0,r2))∩D-1(0, +∞)=? 類似地, 可以使用一致持續性理論得到系統(2)在b=0時的一致持續性, 證明省略. 定理6設d1,d2,r1,r2,q>0且r1>ar2. 若b=0, 則系統(2)是一致持續的, 即存在正常數η, 使得 本節首先通過數值模擬驗證我們的理論研究結果. 取定參數 (I)d1=0.15,d2=0.1,r1=4,r2=3,a=0.5,c=0.2,l=10. 此時r1>ar2, 當b=0時, 由圖1(a)可知, 系統對任意的q>0都是一致持續的, 該結果與定理6相符; 當b=1時, 由圖1(b)可知, 存在一個臨界的流速, 使得當流速小于此臨界值時, 系統是一致持續的, 當流速大于此臨界值時, 捕食者種群平均密度是3, 食餌種群將會滅絕, 該結果與定理4和定理5相符. (II)d1=0.15,d2=0.1,r1=1,r2=3,a=0.5,c=0.2,l=10. 此時r1>ar2, 由圖1(c)可知, 對任意的q>0和b=0.1, 捕食者種群平均密度總是3, 食餌種群總會滅絕, 該結果與定理4相符. 其次, 我們通過數值模擬研究了不同流速對種群空間分布的影響. 選擇參數組(I), 當b=0時, 種群是一致持續的. 但由圖2可知, 隨著流速變大, 種群的空間分布會發生變化, 且隨著流速增加食餌種群會聚集在河流的下游, 由于可用資源減少, 使得種群總的數量降低, 因此對流的增加不利于種群的繁衍. 圖1 系統(2)關于流速q的分支圖 圖2 b=0時不同流速下的種群密度分布圖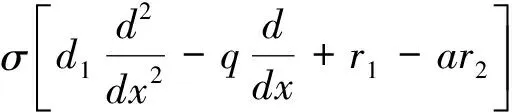
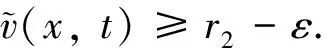
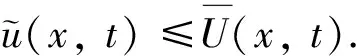
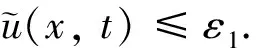
3 系統的一致持續性
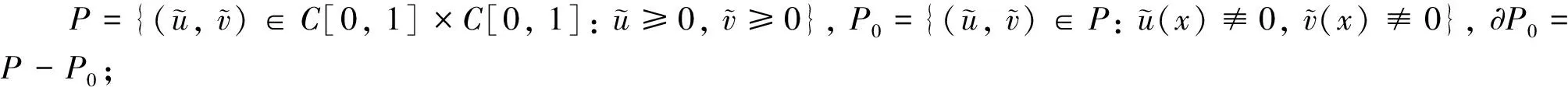
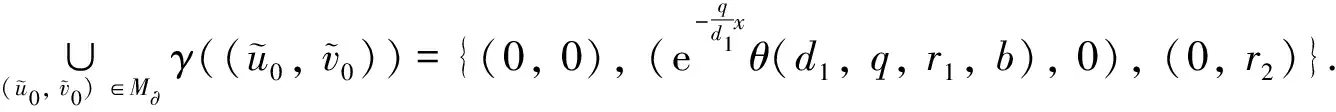
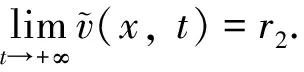
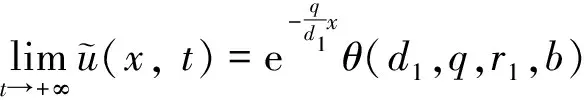
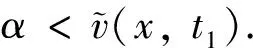
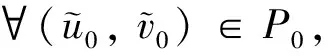
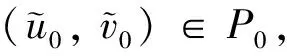
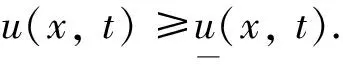

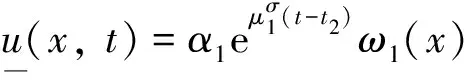
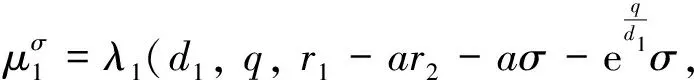

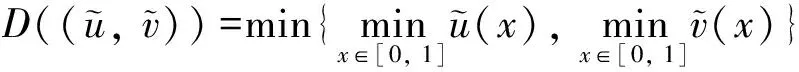
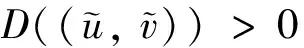

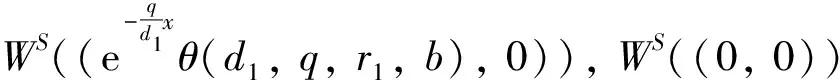
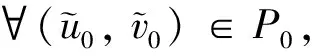
4 數值模擬