高等數(shù)學(xué)理論應(yīng)用于實(shí)際的教學(xué)研究

毛旭強(qiáng)　林海嬋

[ 作者簡(jiǎn)介 ]

毛旭強(qiáng)，男，四川樂(lè)山人，海南大學(xué)理學(xué)院，講師，碩士，研究方向：基礎(chǔ)數(shù)學(xué)。

林海嬋，女，海南昌江人，海南大學(xué)理學(xué)院，講師，碩士，研究方向：應(yīng)用數(shù)學(xué)。

[ 基金項(xiàng)目 ]

海南省自然科學(xué)基金青年基金項(xiàng)目（120QN175），海南大學(xué)理學(xué)院教育教學(xué)改革研究項(xiàng)目（LXG202009）。

[ 摘要 ]

本文通過(guò)高等數(shù)學(xué)理論在實(shí)際中的幾個(gè)應(yīng)用，研究在教學(xué)中將高等數(shù)學(xué)理論與現(xiàn)實(shí)應(yīng)用相結(jié)合，激發(fā)學(xué)生的學(xué)習(xí)興趣，培養(yǎng)學(xué)生主動(dòng)思考和分析問(wèn)題的能力。

[ 關(guān)鍵詞 ]

導(dǎo)數(shù);曲率;漸屈線;漸伸線;自治微分方程;無(wú)窮級(jí)數(shù)

中圖分類號(hào)：O13

文獻(xiàn)標(biāo)識(shí)碼：A

DOI：10.3969/j.issn.1672-0407.2022.03.037

高等數(shù)學(xué)是高校重要的基礎(chǔ)學(xué)科，因其含有的微積分、微分方程、級(jí)數(shù)等內(nèi)容被廣泛應(yīng)用于各個(gè)領(lǐng)域，所以高等數(shù)學(xué)是大學(xué)很多專業(yè)的核心基礎(chǔ)課程。高等數(shù)學(xué)作為一種數(shù)學(xué)課程，課程內(nèi)容比較抽象，老師在講授的過(guò)程中，往往偏向于定理和性質(zhì)的推導(dǎo)與證明，對(duì)其在實(shí)際中的應(yīng)用涉及較少。這導(dǎo)致學(xué)生在學(xué)習(xí)過(guò)程中會(huì)感覺枯燥，而學(xué)習(xí)完課程后，很多學(xué)生只掌握了純數(shù)學(xué)問(wèn)題的計(jì)算與證明，卻不了解這些理論在現(xiàn)實(shí)中的作用，部分人甚至發(fā)出高數(shù)無(wú)用的感嘆。因此如何讓教學(xué)過(guò)程既有用又有趣就顯得尤其重要，通過(guò)現(xiàn)實(shí)實(shí)例來(lái)講解理論是實(shí)現(xiàn)有趣教學(xué)的重要途徑。

目前國(guó)內(nèi)經(jīng)濟(jì)社會(huì)發(fā)展進(jìn)入一個(gè)新時(shí)期，進(jìn)行供給側(cè)改革和產(chǎn)業(yè)升級(jí)需要科技的支撐，大學(xué)作為科技產(chǎn)出的重要單位，理應(yīng)為國(guó)家發(fā)展盡一份力，高等數(shù)學(xué)作為一門基礎(chǔ)學(xué)科，只有面向應(yīng)用，才能做到學(xué)以致用，才能在各行各業(yè)中發(fā)揮作用。本文通過(guò)高等數(shù)學(xué)理論在數(shù)學(xué)建模和工業(yè)上的幾個(gè)應(yīng)用，以期在教學(xué)中將高等數(shù)學(xué)理論與現(xiàn)實(shí)進(jìn)行結(jié)合，激發(fā)學(xué)生的學(xué)習(xí)興趣，培養(yǎng)學(xué)生主動(dòng)思考和分析問(wèn)題的能力。

1 利用導(dǎo)數(shù)判斷實(shí)驗(yàn)數(shù)據(jù)與常見函數(shù)的擬合，實(shí)現(xiàn)對(duì)實(shí)驗(yàn)數(shù)據(jù)的建模

在研究中，對(duì)實(shí)驗(yàn)數(shù)據(jù)進(jìn)行建模可以厘清變量之間的聯(lián)系，并且一旦建模成立，還能利用模型對(duì)未來(lái)數(shù)據(jù)進(jìn)行預(yù)測(cè)，利用導(dǎo)數(shù)判斷實(shí)驗(yàn)數(shù)據(jù)是否擬合函數(shù)是數(shù)學(xué)建模中經(jīng)常使用的方法。假設(shè)為實(shí)驗(yàn)數(shù)據(jù)，令。

1.1 利用導(dǎo)數(shù)判斷變量間的聯(lián)系是否為

當(dāng)時(shí)，，即，

因此，如果根據(jù)實(shí)驗(yàn)數(shù)據(jù)得出常數(shù)，則說(shuō)明與間具有直線關(guān)系。

1.2 利用導(dǎo)數(shù)判斷變量間的聯(lián)系是否為

所以如果實(shí)驗(yàn)數(shù)據(jù)得出常數(shù)，則說(shuō)明。

1.3 利用導(dǎo)數(shù)判斷變量間的聯(lián)系是否為

當(dāng)時(shí)，在等式兩邊取對(duì)數(shù)，有，令，則，此時(shí)，所以如果實(shí)驗(yàn)室數(shù)據(jù)顯示常數(shù)，則說(shuō)明 。

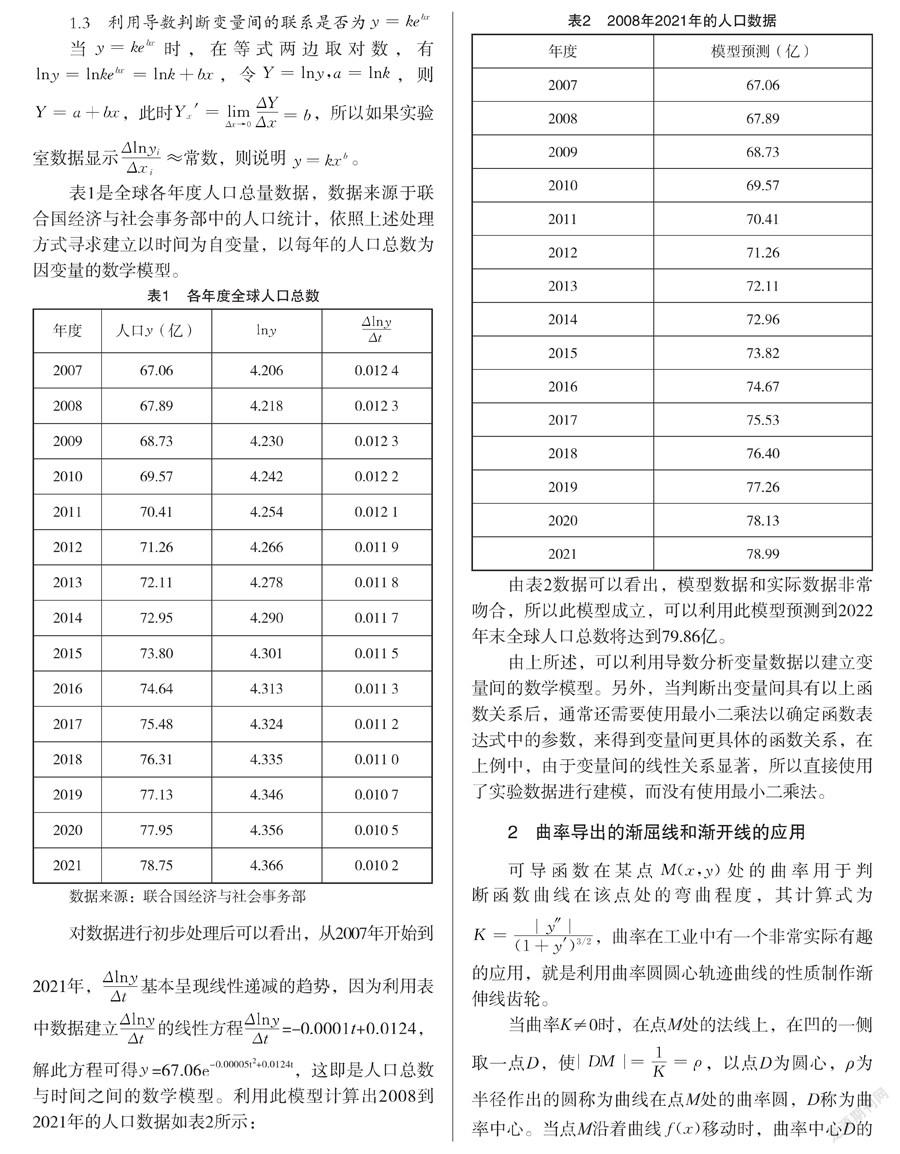
表1是全球各年度人口總量數(shù)據(jù)，數(shù)據(jù)來(lái)源于聯(lián)合國(guó)經(jīng)濟(jì)與社會(huì)事務(wù)部中的人口統(tǒng)計(jì)，依照上述處理方式尋求建立以時(shí)間為自變量，以每年的人口總數(shù)為因變量的數(shù)學(xué)模型。

對(duì)數(shù)據(jù)進(jìn)行初步處理后可以看出，從2007年開始到2021年，基本呈現(xiàn)線性遞減的趨勢(shì)，因?yàn)槔帽碇袛?shù)據(jù)建立的線性方程=-0.0001t+0.0124，解此方程可得=67.06e-0.00005t2+0.0124t，這即是人口總數(shù)與時(shí)間之間的數(shù)學(xué)模型。利用此模型計(jì)算出2008到2021年的人口數(shù)據(jù)如表2所示：

由表2數(shù)據(jù)可以看出，模型數(shù)據(jù)和實(shí)際數(shù)據(jù)非常吻合，所以此模型成立，可以利用此模型預(yù)測(cè)到2022年末全球人口總數(shù)將達(dá)到79.86億。

由上所述，可以利用導(dǎo)數(shù)分析變量數(shù)據(jù)以建立變量間的數(shù)學(xué)模型。另外，當(dāng)判斷出變量間具有以上函數(shù)關(guān)系后，通常還需要使用最小二乘法以確定函數(shù)表達(dá)式中的參數(shù)，來(lái)得到變量間更具體的函數(shù)關(guān)系，在上例中，由于變量間的線性關(guān)系顯著，所以直接使用了實(shí)驗(yàn)數(shù)據(jù)進(jìn)行建模，而沒有使用最小二乘法。

2 曲率導(dǎo)出的漸屈線和漸開線的應(yīng)用

可導(dǎo)函數(shù)在某點(diǎn)處的曲率用于判斷函數(shù)曲線在該點(diǎn)處的彎曲程度，其計(jì)算式為，曲率在工業(yè)中有一個(gè)非常實(shí)際有趣的應(yīng)用，就是利用曲率圓圓心軌跡曲線的性質(zhì)制作漸伸線齒輪。

當(dāng)曲率K≠0時(shí)，在點(diǎn)M處的法線上，在凹的一側(cè)取一點(diǎn)D，使，以點(diǎn)D為圓心，ρ為半徑作出的圓稱為曲線在點(diǎn)M處的曲率圓，D稱為曲率中心。當(dāng)點(diǎn)M沿著曲線移動(dòng)時(shí)，曲率中心D的軌跡曲線稱為曲線的漸屈線，曲線稱為漸伸線。

設(shè)曲率中心D的坐標(biāo)為（α，β），根據(jù)曲率圓的定義可知

依據(jù)參數(shù)方程求導(dǎo)公式可求出，從而，由此可知，漸屈線G的切線與漸伸線 的切線垂直，如圖一所示。

利用漸屈線G的切線與漸伸線垂直這一性質(zhì)，工業(yè)中將之應(yīng)用于設(shè)計(jì)漸伸線齒輪。如果將齒輪轉(zhuǎn)盤邊緣曲線作為漸屈線，以邊緣曲線的漸伸線作為轉(zhuǎn)盤齒輪，利用漸屈線切線與漸伸線切線相垂直這一特性，當(dāng)齒輪轉(zhuǎn)動(dòng)時(shí)，齒輪咬合處力的方向正好與齒輪垂直，從而可以得到最大力矩，如圖二所示。

3 利用自治微分方程的相直線和平衡點(diǎn)建模

微分方程是研究自然和社會(huì)的有力工具，在科學(xué)研究和實(shí)際生產(chǎn)中，很多問(wèn)題可以歸結(jié)為用微分方程表示的數(shù)學(xué)模型，在講授微分方程時(shí)結(jié)合實(shí)例進(jìn)行講解有助于培養(yǎng)學(xué)生的建模思維。

求解微分方程的過(guò)程就是要求出滿足方程的函數(shù) 。為了方便求出，在微分方程中通常表示為自變量的函數(shù)，例如，如果在一個(gè)微分方程中表達(dá)式中只含有而不含有，這種微分方程就稱為自治微分方程，例如。在處理實(shí)際問(wèn)題時(shí)，我們往往最先觀察到的是因變量的變化，此時(shí)可以考慮用自治微分方程的相直線和穩(wěn)定點(diǎn)的思想來(lái)進(jìn)行建模分析。

在自治方程中，使0的值稱為方程的平衡點(diǎn)，例如上面方程中的0與20。平衡點(diǎn)所對(duì)應(yīng)的直線稱為相直線。相直線可以用于分析微分方程的解函數(shù)的變化趨勢(shì)。

例如，在方程（20-）中，易知，當(dāng)解函數(shù)（）位于相直線20上方時(shí)，<0，此時(shí)（）單調(diào)遞減;而當(dāng)解函數(shù)（）位于相直線20下方時(shí)，>0，此時(shí)（）單調(diào)遞增，如圖三所示。假設(shè)表示現(xiàn)實(shí)中水壺里水的溫度，室內(nèi)溫度是20攝氏度，那么圖三表明，當(dāng)水溫高于室溫時(shí)，隨著時(shí)間推移，水溫會(huì)下降直到達(dá)到室內(nèi)溫度;而當(dāng)水溫低于室溫時(shí)，隨著時(shí)間推移，水溫會(huì)上升，直到達(dá)到室內(nèi)溫度。

相直線建模在現(xiàn)實(shí)中廣泛應(yīng)用于分析有限資源下的群體增長(zhǎng)、一條信息在人群中的擴(kuò)散情況、工業(yè)中化學(xué)物的自催化反應(yīng)等等。在分析有限資源下的群體增長(zhǎng)時(shí)，在現(xiàn)實(shí)環(huán)境中，由于受到資源的限制，種群數(shù)無(wú)法無(wú)限增長(zhǎng)，當(dāng)種群數(shù)目小于環(huán)境的最大負(fù)載能力時(shí)，種群數(shù)可以一直增長(zhǎng);但當(dāng)種群數(shù)超過(guò)環(huán)境的最大負(fù)載能力時(shí)，種群數(shù)將下降。在理論上種群數(shù)將圍繞著環(huán)境的最大負(fù)載值進(jìn)行波動(dòng)，這正好是相知線模型的特征。

假設(shè)環(huán)境對(duì)某一種群的最大負(fù)載數(shù)為M，種群當(dāng)前的數(shù)目為，由上可知，當(dāng)<M時(shí)，（t）>0，種群數(shù)增長(zhǎng);當(dāng)>M時(shí)，（t）<0，種群數(shù)下降。其對(duì)應(yīng)的自治微分方程模型為：

，此模型中0及M 時(shí)種群增長(zhǎng)速度為零，直線0與M為該模型方程的相直線。相直線M與上圖中的相直線20類似，當(dāng)時(shí)間 t 增加時(shí)，曲線會(huì)趨于M，所以點(diǎn)M 又稱為方程的穩(wěn)定平衡點(diǎn)。解此微分方程可得，其中當(dāng)>M時(shí)，r <0;當(dāng)<M時(shí)，r>0。在自治微分方程兩邊繼續(xù)求導(dǎo)，可得，從而當(dāng) 時(shí)，此時(shí)曲線是凹曲線;當(dāng)時(shí)，此時(shí)曲線是凸曲線;當(dāng)>M時(shí)，曲線時(shí)凹曲線，如圖四所示。這表明，當(dāng)時(shí)種群增速較快，當(dāng)>時(shí)種群增速放緩，并且逐漸趨于0，穩(wěn)定在M;而當(dāng)>M時(shí)，越大種群減速越快，隨著時(shí)間推移減速放緩，逐漸趨于零，穩(wěn)定在M。

4 無(wú)窮級(jí)數(shù)在現(xiàn)實(shí)中的應(yīng)用

無(wú)窮級(jí)數(shù)是一個(gè)強(qiáng)有力的工具，利用它使我們能將函數(shù)表示成無(wú)窮多項(xiàng)式或者無(wú)窮三角函數(shù)項(xiàng)，并且當(dāng)我們把它截?cái)喑捎邢揄?xiàng)時(shí)，還可以進(jìn)一步分析產(chǎn)生的誤差，這些特性使得無(wú)窮級(jí)數(shù)在醫(yī)藥、經(jīng)濟(jì)、熱流、振動(dòng)、信號(hào)傳輸?shù)雀餍懈鳂I(yè)中都有重要的作用。通過(guò)實(shí)例的學(xué)習(xí)，可以讓學(xué)生為級(jí)數(shù)在科學(xué)和數(shù)學(xué)中應(yīng)用打好良好的基礎(chǔ)。

4.1 無(wú)窮級(jí)數(shù)在醫(yī)學(xué)中的應(yīng)用

很多慢性病人每天都要按醫(yī)囑服用一定劑量的某種藥物，每天都有一定比例的藥物通過(guò)各種渠道排泄掉，醫(yī)生往往需要根據(jù)病人長(zhǎng)期服藥后體內(nèi)藥量維持水平來(lái)確定病人的服藥量。

假設(shè)病人每天的服藥量為m，每天有比例的藥物通過(guò)各種渠道排泄掉，則服藥第一天，病人體內(nèi)藥量為m;服藥第二天，病人體內(nèi)藥量為;服藥第三天，病人體內(nèi)藥量為;…，依此類推，長(zhǎng)期服藥后，病人體內(nèi)的藥量為，這是一個(gè)公比為的無(wú)窮級(jí)數(shù)，利用等比級(jí)數(shù)求和公式可知。由上可知，如果病人每天服藥量為1 mg，排泄率為25 %，那么長(zhǎng)期服藥后，病人體類的藥量水平將是4 mg。所以醫(yī)生可以根據(jù)病人體內(nèi)藥量水平，結(jié)合病人的病情來(lái)確定病人的服藥量。

4.2 無(wú)窮級(jí)數(shù)在經(jīng)濟(jì)中的應(yīng)用

無(wú)窮級(jí)數(shù)在經(jīng)濟(jì)中可用于依年復(fù)利計(jì)算時(shí)金融投資中的投入和收益。

假設(shè)投資年回報(bào)率為，依年復(fù)利計(jì)算，若投資方希望通過(guò)投資S萬(wàn)元，實(shí)現(xiàn)第一年提取a+b萬(wàn)元，第二年提取a+2b萬(wàn)元，…，第n年提取a+nb萬(wàn)元，并能按此規(guī)律一直提取下去，為實(shí)現(xiàn)這個(gè)目標(biāo)需要確定最初的投資額S。因?yàn)閚年后的提取值為a+nb，假設(shè)a+nb是由投資額S中的部分金額Sn 通過(guò)年復(fù)利計(jì)算產(chǎn)生的，則無(wú)窮級(jí)數(shù)，無(wú)窮級(jí)數(shù)，利用級(jí)數(shù) ，將代入，有，于是可得。由上，如果投資回報(bào)率r=0.1，a=10，b=10，則為實(shí)現(xiàn)目標(biāo)，最初的投資額需要1200萬(wàn)元。

5 結(jié)語(yǔ)

以上只是闡述了高等數(shù)學(xué)在現(xiàn)實(shí)中的幾個(gè)應(yīng)用，實(shí)際上，現(xiàn)實(shí)中的對(duì)高等數(shù)學(xué)理論的使用非常廣泛，從經(jīng)濟(jì)學(xué)到金融、從物理到航天、從工程設(shè)計(jì)到信號(hào)傳輸、從醫(yī)藥分析到化學(xué)反應(yīng)等等，各行各業(yè)都有大量應(yīng)用。因此，加強(qiáng)高等數(shù)學(xué)教學(xué)中理論知識(shí)實(shí)際應(yīng)用的講解將激發(fā)學(xué)生的學(xué)習(xí)興趣，增強(qiáng)學(xué)生分析問(wèn)題解決問(wèn)題的能力，為學(xué)生進(jìn)一步的發(fā)展打下良好的基礎(chǔ)。

參考文獻(xiàn)

[1]同濟(jì)大學(xué)數(shù)學(xué)系. 高等數(shù)學(xué)[M]. 北京： 高等教育出版社，2007.

[2]韓漢鵬，馬少軍，徐光輝. 大學(xué)數(shù)學(xué)——微積分[M]. 北京： 高等教育出版社，2010.

[3]王志剛，李文雅. 高等數(shù)學(xué)[M]. 北京： 高等教育出版社，2014.

[4]李建平. 微積分[M]. 北京： 北京大學(xué)出版社，2018.

[5]張?zhí)斓拢醅|. 高等數(shù)學(xué)[M]. 北京： 人民郵電出版社，2020.

[6]姜啟源，謝金星，葉俊. 數(shù)學(xué)模型[M]. 北京： 高等教育出版社，2018.