沿海混凝土結構氯離子對流區深度計算模型

郝 磊，陳 峰，彭文鋒，查 斌

(1.長安大學公路學院，西安 710064；2.在役長大橋梁安全與健康國家重點實驗室，南京 211112)

0 引 言

沿海地區存在的大規模混凝土基礎設施都面臨嚴峻的氯離子侵蝕問題，其會影響混凝土結構的耐久性甚至安全性，因此引起了廣泛的關注與討論。Collepardi等[1]率先提出借助Fick定律解釋混凝土內部氯離子擴散傳輸的現象，經眾多學者[2-3]研究發現，處于飽水狀態的混凝土，其內部氯離子傳輸狀態可以通過Fick第二定律較好的展現。

干濕交替環境中，混凝土內部維持非飽水狀態，此時氯離子不但以擴散作用進入混凝土，還會受到對流效應的影響。混凝土構件在與外界水相接觸的瞬間，表面將主要發生由毛細吸附水形成的對流，在水分流動的過程中將攜帶大量氯離子，從而導致定向遷移。然后在濕度梯度的影響下，氯離子以非飽和滲流的方式，不斷侵入混凝土。

處于干濕交替環境中的混凝土構件，其鋼筋銹蝕問題最為嚴重，因此研究混凝土處于干濕交替環境中其內部氯離子的傳輸規律具有重要價值。於德美等[4]結合水分擴散與稀物質傳輸方程，得到了以混凝土內部水分飽和度為基本變量的氯離子傳輸方程。申林等[5]根據水分遷移的特點，推導出氯離子傳輸的對流擴散耦合方程，利用細觀隨機混凝土模型研究了骨料對混凝土內部氯離子分布情況的影響。李榮濤[6]基于有限元方法建立了多相耦合的氯離子侵蝕模型。

上述研究主要通過求解由偏微分方程組組成的計算模型來描述干濕交替環境中氯離子的傳輸過程，雖然能從機理上反映氯離子的傳輸，但實際橋梁結構服役時間一般高達數十年，采用這樣的模型進行計算用時較長，難以直接指導混凝土結構耐久性設計。考慮到使用方便和計算簡明，國內外研究者仍傾向使用Fick第二定律的解析方程來描述在非飽和態下混凝土內部氯離子傳輸情況。

混凝土的低滲透性特點，使得其內部的水輸送與外部環境變化存在滯后現象。干濕交替的自然條件僅能在混凝土表面有限深度范圍內產生影響，該深度可定義為氯離子傳輸的對流區深度Δx。基于該假定，Andrade等[7]、Matthews等[8]、陸春華等[9]將混凝土氯離子分布區域分為對流區和擴散區兩個部分，通過Δx對Fick第二定律解析解進行修正，整理得到簡化計算模型來預測干濕交替環境混凝土中的氯離子傳輸行為。

在該模型中，雖將混凝土中的氯離子傳輸分為對流區和擴散區，但主要造成影響的是內部的擴散作用，即描述Δx深度范圍以外的氯離子濃度。模型的適用性很大程度上取決于對流區深度及模型中重要技術參數的合理取值。

Duracrete等[10]根據結構維修成本，結合環境特征給出了混凝土結構不同服役環境對應的Δx經驗取值。馮超等[11]研究發現由于干濕循環次數的增多，對流區深度會趨于穩定，根據干濕循環90次的氯離子傳輸計算結果，以干濕循環周期為自變量，得到計算對流區深度的方程。Gao等[12]通過對270個試驗樣本假設檢驗，得出對流區深度滿足耿貝爾分布，均值等于3.99 mm。高延紅等[13]根據對自然潮差環境的現場測試成果，總結出對流區深度的隨機性可用正態分布描述，均值為3.76 mm。龐森等[14]使用數值方法求解，得到飽和度峰值位置不斷向混凝土深處移動，并最終穩定在20 mm深度左右。崔釗瑋等[15]設計試驗來模擬浪濺區混凝土構件的服役狀況，考慮包括混凝土開裂、干濕循環和氯鹽環境等因素，發現氯離子分布曲線在10～15 mm范圍內出現峰值。

綜上所述，對流區深度Δx是修正Fick第二定律簡化計算模型的關鍵參數，即當Δx確定后，氯離子的侵蝕問題就可以簡化為用飽和混凝土擴散方程進行近似求解。然而目前有關Δx取值的規定尚未成熟，大多依據短期試驗測試與經驗判斷直接將其假定為定值，忽略了溫度、混凝土材料構成、濕度等因素的影響，對簡化計算的精度產生較大誤差。因而，深入研究對流區深度將是提高簡化計算模型準確度的關鍵。本文在建立混凝土細觀尺度求解模型的基礎上，綜合考慮水分遷移、氯離子傳輸和溫度場等因素，建立了干濕交替區域混凝土細觀尺度氯離子侵蝕計算模型，對Δx在各顯著影響因素變化下反映出的規律進行分析，給出了考慮服役時間、日平均氣溫和干燥濕潤時間比等影響參數的對流區深度Δx時變計算模型，以期對干濕交替環境中混凝土氯鹽侵蝕簡化計算模型進行精確求解提供參考。

1 非飽和混凝土氯離子傳輸數值模擬計算模型

在濃度梯度的驅動下，氯離子從外界環境向混凝土內部擴散，同時隨著混凝土孔隙結構中水分的自由移動而發生對流，特別是當混凝土表面干燥時，水分蒸發使得氯離子在向內部擴散的同時也向表層聚集，此區域范圍氯離子侵蝕整體呈現非飽和混凝土傳輸特征。以混凝土細觀骨料模型為基礎，引入水分遷移模型、氯離子傳輸模型和環境溫度場模型來討論干濕交替區域氯離子傳輸的規律將是精確分析該傳輸模式的更為有效的方法。

1.1 細觀骨料模型

比較于宏觀與微觀尺度，細觀尺度的有限元模型既可以充分考慮混凝土內部非均質的特性，也揭示了其內部構造和宏觀力學特征、擴散和滲透特征間的相互關系，同時計算量也比微觀尺度小。所以，從細觀尺度上模擬混凝土的非均質性，已被大部分研究者認可[16]。

本文為考慮混凝土非均質性對氯離子傳輸的影響，建立了細觀分析模型。細觀尺度下，混凝土一般被看作是粗骨料、水泥和二者之間的界面過渡區(interfacial transition zone， ITZ)組成的多相復合物。由于ITZ厚度相對小，并且氯離子透過分界層時的擴散量也更少，所以，在該計算模型中暫不考慮對骨料邊界層的影響。同時，由于混凝土中大部分的粗骨料都很密實，氯離子很難擴散進入其中，因此可假定粗骨料中氯離子的擴散系數為零。為研究方便，本文假定混凝土由粗骨料和砂漿組成，取局部樣本研究尺寸為100 mm×100 mm，使用AutoCAD軟件按照混凝土試樣照片繪制二維混凝土細觀骨料有限元模型，如圖1所示。

圖1 混凝土樣本細觀骨料模型Fig.1 Meso-aggregate model of concrete samples

1.2 干濕交替分析模型

水分本身作為氯離子傳輸的主要介質，在流動的同時也會搬運侵蝕性物質。所以，在混凝土結構性能的長期演化過程中，了解水分在混凝土中的儲存和運移規律具有舉足輕重的意義。

非飽水狀態的混凝土與外部環境水相接觸的瞬間，其表面以毛細作用吸收水分，進而在濕度梯度的影響下，以非飽和滲流的形式向混凝土內輸送，這一過程可用擴展的Darcy定理[17]來解釋，水分滲流速度(Js)可表示為：

(1)

式中：Dm為水分擴散系數，m2/s；x為擴散深度，mm；s為混凝土含水飽和度。

處于干濕交替區域的混凝土構件，其內孔隙飽和度將保持非平衡狀態，并由此產生了濕度梯度場，在場的驅動作用下混凝土內部氯離子通過擴散和對流的方式遷移。氯離子在非飽和狀態下的輸運過程可用對流擴散方程說明：

(2)

式中：C為氯離子濃度(占混凝土質量百分數)，%；Deff為氯離子在飽水混凝土中的擴散系數，m2/s。

(3)

公式(2)為二階偏微分方程，通過分析混凝土結構服役的自然環境狀況，可以確定出計算模型的初始條件和邊界條件，之后可以借助有限元法近似求解。水分傳輸和氯離子遷移以耦合的方式存在，因此對于二者的邊界條件需同時定義。從結構長期服役來看，自然環境中的干濕交替條件可視為等周期干燥和濕潤交替過程，即較長時間周期內可認為干燥階段、濕潤階段時間趨于穩定。各階段傳輸方式如式(4)、(5)所示。

混凝土處于干燥階段時，水分能夠在混凝土表面自由交換，而氯離子則不能從混凝土表面進入大氣環境。

(4)

式中：RH為空氣相對濕度；r為飽和度修正系數；u為水分對流速度。

濕潤階段混凝土邊界處于飽水狀態，可認為表層混凝土孔隙液內的氯離子濃度與構件表面積聚的氯離子濃度Cs(t)相等。

(5)

1.3 環境溫度場模型

不同溫度條件下水分子和氯離子的活化能有所不同，而氣溫的波動也會對水分擴散以及氯離子遷移造成影響。目前有關耐久性的研究主要以某一區域的環境平均溫度代替結構實際溫度場，但實際混凝土結構內部溫度分布往往隨時間和空間的變化存在差異，表現為非恒定的值。

根據能量守恒定律，混凝土結構導熱過程可用Fourier方程[18]表示：

(6)

式中：ρ為混凝土密度；c為混凝土比熱容；Φ為混凝土內部熱源。

地球因存在自轉和公轉現象，形成了太陽輻射能量的周期性變化，本文將自然環境溫度變化簡化為正弦函數形式表示，變化周期為24 h[19]：

(7)

式中：Tav為日平均氣溫，K；Tam為氣溫日變化幅值，K。

1.4 非飽和混凝土氯離子傳輸計算分析

基于COMSOL軟件建立非飽和混凝土氯離子傳輸分析數值計算模型，綜合考慮了水分遷移、氯離子傳輸和溫度變化的影響，并以文獻[20]的試驗數據作為計算分析對象驗證模型的有效性。文獻[20]中G3S1試驗組數據中的Cl-含量峰值及對流區深度現象明顯，便于驗證對流計算結果，故選取該組試驗條件進行數值分析，試驗中試件尺寸為100 mm×100 mm×400 mm，混凝土的強度等級為C30，水灰比為0.49，除腐蝕面外其他各面均用環氧樹脂密封，保證氯離子沿一維方向輸運。G3S1試驗組單次循環持續48 h，干濕時間比為3 ∶1，具體的試驗方案見表1。

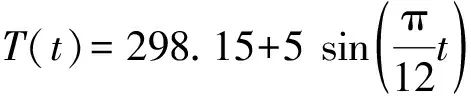
表1 干濕循環試驗方案Table 1 Dry-wet cycle experiment scheme

在模擬計算試驗過程時，按照試驗設計參數進行干濕交替及溫度場循環，每個干濕過程的求解結果作為下一個干濕循環過程的初始條件。整個試驗過程中混凝土內部氯離子分布的時空變化情況即可通過求解給出明確的分析結果，循環100 d時混凝土內部氯離子分布情況如圖3所示。濕潤階段隨著混凝土內部達到飽水狀態，在濃度梯度促使下環境溶液中的氯離子會逐漸向混凝土深處遷移。混凝土表層水分在外界環境干燥時會逐漸蒸發，由此引起的對流作用使得混凝土淺層區域的氯離子出現反向傳輸，隨著內部孔隙液的蒸發不斷向表面轉移。表層混凝土內的氯離子在干濕交替的循環過程中持續累積，同時更深層區域的氯離子在擴散作用下仍保持著向內部傳遞。

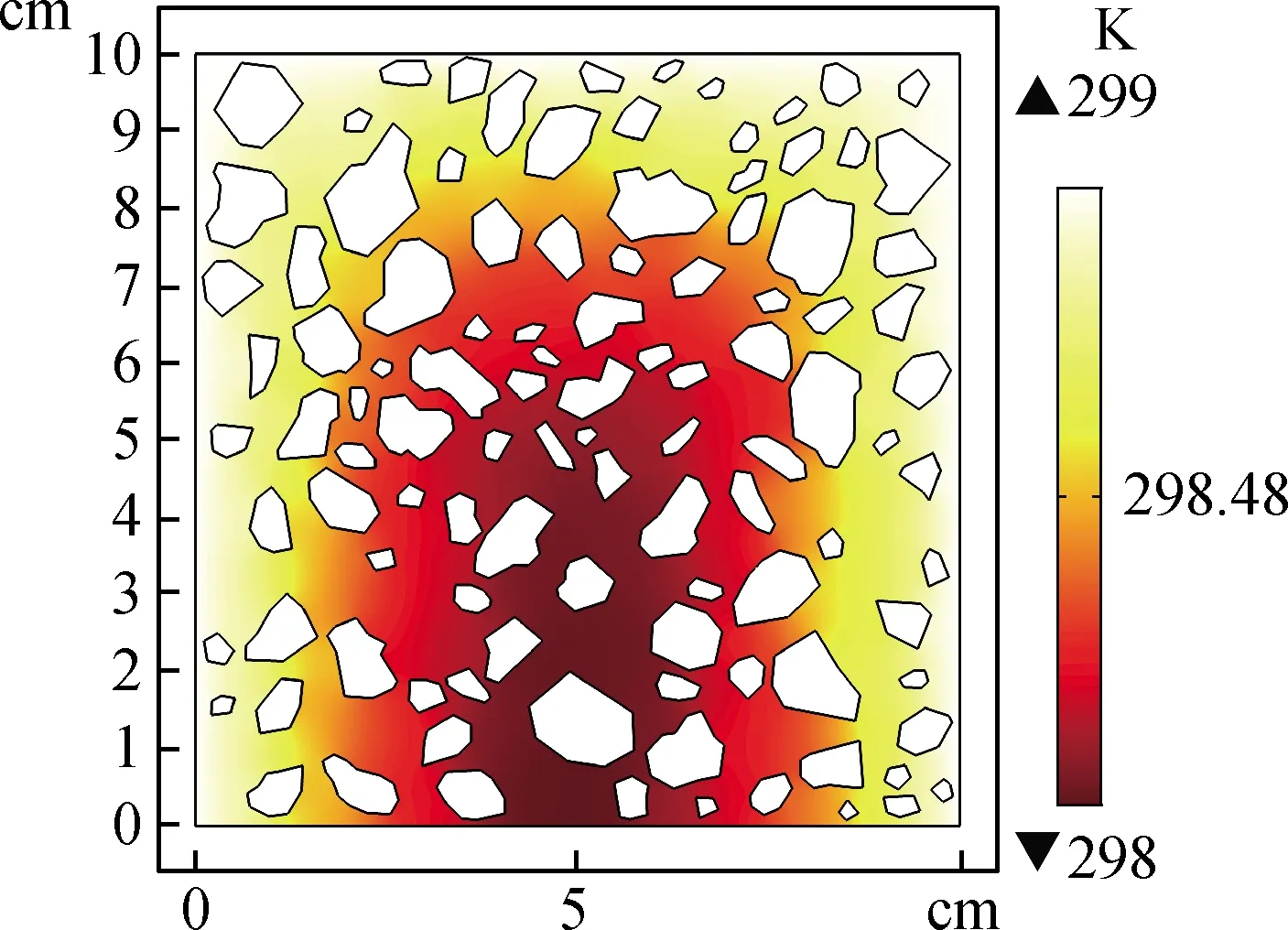
圖2 混凝土內部溫度場示意圖Fig.2 Schematic diagram of temperature field in concrete

圖3 循環100 d時混凝土內部氯離子分布示意圖Fig.3 Schematic diagram of distribution of chloride ion in concrete after 100 d

圖4 試驗結果與模型計算結果比較Fig.4 Comparison between experimental results and model calculation results

借助本文的非飽和混凝土氯離子傳輸計算模型，采用文獻[20]同樣的試驗條件分別對照分析了10 d、20 d、40 d、60 d、80 d、100 d共6組時變氯離子分布計算結果，與試驗結果具體對比情況如圖4所示。圖中數據顯示，無論是氯離子的淺層分布特征、積聚速度，還是整個區域范圍內的氯離子分布情況，除了時間周期較短的10 d、20 d兩組數據的表層氯離子峰值濃度數據有一定偏差外(上述偏差由于文獻[20]的混凝土試件內部初始飽和度無法確定，同時數值模型難以體現混凝土水分擴散系數與氯離子擴散系數在初期的變化復雜所引起)，其他數據都顯示了較強的一致性。圖中數值計算結果和試驗結果均表明，在干濕交替環境下，距離混凝土表面一定深度處都產生了氯離子濃度峰值，且隨著時間推移該峰值所對應的深度已基本穩定。計算結果與試驗數據較好的一致性表明了隨著服役時間的增長，本分析方法及數值模型具有較高的準確性，經第三方試驗驗證可以足夠精確地描述干濕交替環境中氯離子的傳輸行為，因此可借助此計算分析模型對非飽和混凝土氯離子傳輸的特性與規律進一步討論分析。

2 基于非飽和混凝土氯離子傳輸機理的對流區深度Δx

不同于浸泡環境的混凝土構件，氯離子進入其內部主要是通過擴散方式。處于干濕交替環境中的混凝土，其內部表現為非飽和狀態，由對流和擴散的耦合作用推動氯離子的遷移。正是由于對流作用的影響，造成了兩種情況中氯離子傳輸的差異。

2.1 對流區的特點

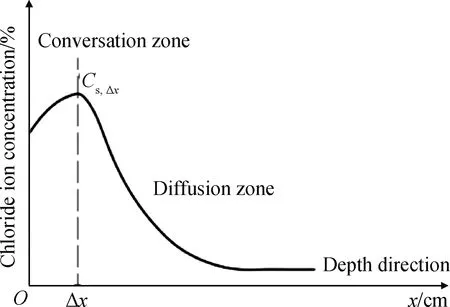
圖5 干濕交替條件下混凝土內部氯離子分布情況Fig.5 Distribution of chloride ions in concrete under dry-wet alternation conditions

干濕交替影響下的對流現象作用于混凝土內部，產生了氯離子濃度的局部峰值，以此點為分水嶺，并根據驅使氯離子傳輸的主要作用形式，把混凝土劃分為對流區和擴散區二部分。由前述的數值分析及試驗結果顯示干濕交替條件下混凝土內部氯離子分布情況的抽象曲線，如圖5所示。

圖5曲線顯示，在0≤x<Δx區間內，氯離子傳輸主要是由對流和擴散耦合作用引起的，曲線逐漸升高至峰值。而在x≥Δx氯離子傳輸主要由擴散作用引起，曲線呈現擴散方程曲線特性。對流區的存在會對混凝土內部氯離子含量的分布情況和數值大小產生相當的影響，因此分析對流區深度是氯離子傳輸計算模型的重要內容。

2.2 對流區深度Δx的分析求解方法

在氯離子傳輸的對流區范圍內，描述擴散作用的Fick第二定律已不再適用。但對流區域深度以外的區域，仍可以足夠精確地認為氯離子以擴散的形式傳輸，符合Fick第二定律。因此，可以通過引入對流區深度Δx和其對應的氯離子濃度Cs,Δx這兩個參數修正完善Fick第二定律解析解，從而通過簡便的計算，預測干濕循環作用下的氯離子分布情況。此模型的重點不是對氯離子的傳輸規律進行完全的描述，而是對Δx以外區域的氯離子濃度進行較為準確的預測。

國際混凝土聯合會(FIB)[8]給出了修正Fick第二定律的簡化計算模型，如式(8)所示，可用于計算預測干濕循環作用下混凝土內部氯離子傳輸。

(8)

式中：Cx,t為混凝土內部氯離子濃度；C0為混凝土內部初始氯離子濃度。

Duracrete[10]結合結構的維修成本總結歸納了Δx的指導經驗值，如表2所示。

表2 Duracrete中關于Δx取值規定Table 2 Duracrete requirements on Δx value

根據前述的非飽和混凝土氯離子傳輸數值計算結果與試驗對比分析顯示出的對流區規律，本文提出了計算Δx的改進方法。

Δx是經驗方法體系的重要參數，但目前有關Δx取值的規定由于缺乏理論支持無法定量，所以一般是通過經驗方法確定其值。事實上由于混凝土內部在干濕循環過程中會出現孔隙液蒸發和滲透等復雜過程，其取值主要與結構服役時間、孔隙結構、干燥濕潤時間比值、混凝土內部溫度場、干燥條件等因素有關。

(1)通過非飽和混凝土氯離子傳輸數值計算模型可得到干濕交替環境下混凝土內部氯離子含量的最大值和對應的影響深度，該深度即為對流區深度Δx的數值。

(2)將影響深度部分扣除，剩余部分即構成了修正的氯離子分布曲線。

(3)以相應的氯離子濃度值Cs,Δx作為邊界條件引入飽水混凝土擴散分析模型中，即可得到基于Fick定律的氯離子分布曲線。

2.3 基于非飽和混凝土氯離子傳輸機理的對流區深度計算方法驗證

為了驗證本文所提出的Δx改進計算方法的有效性，同時采用非飽和混凝土氯離子傳輸數值計算模型和基于Fick定律的飽水混凝土擴散分析模型進行計算，分析對比相應的計算結果。

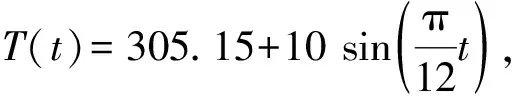
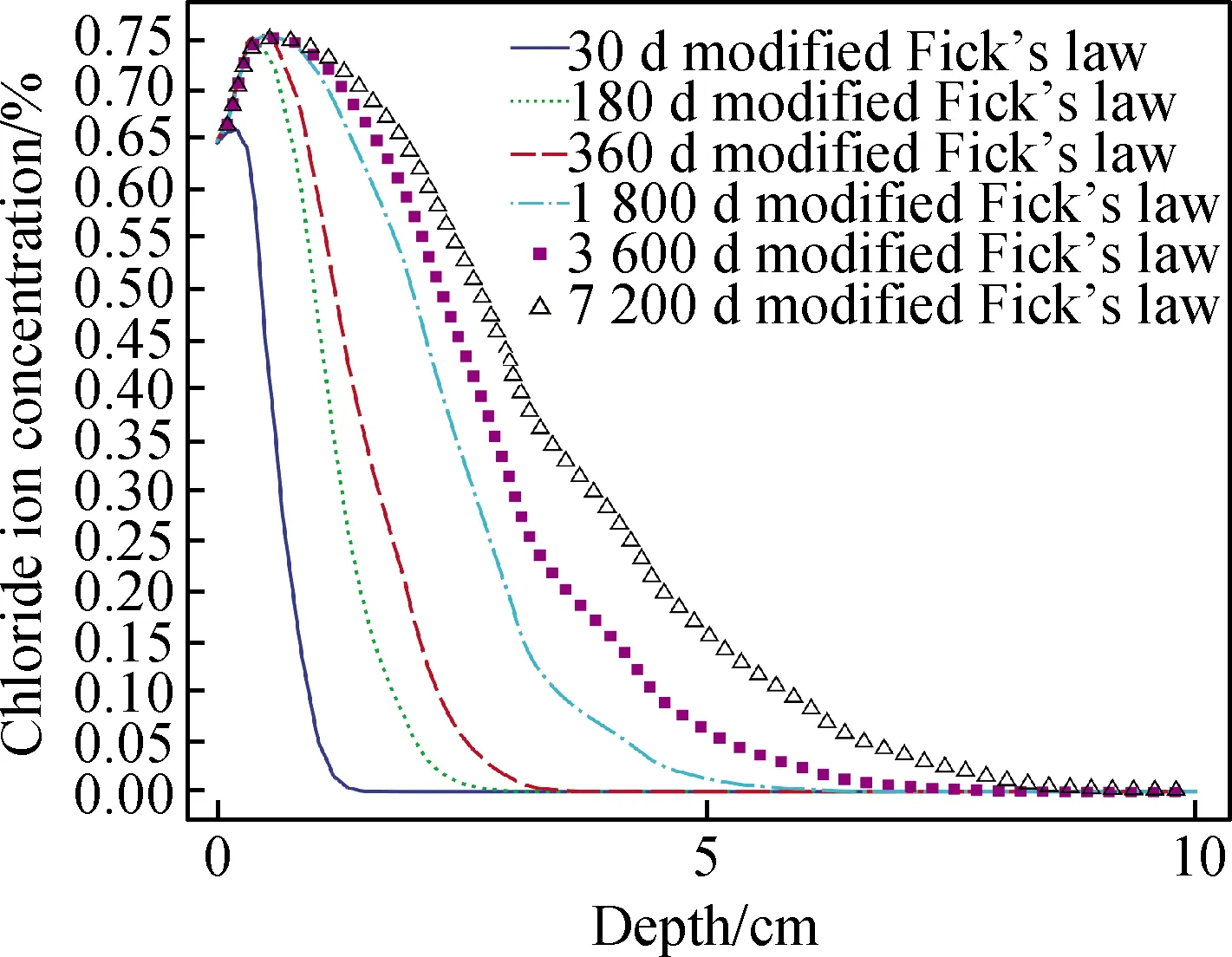
圖6 非飽和混凝土氯離子傳輸模型計算結果Fig.6 Calculation results of chloride ion transport model for unsaturated concrete

圖7 飽水混凝土擴散分析模型計算結果Fig.7 Calculation results of diffusion analysis model for saturated concrete

為了驗證修正氯離子擴散曲線與飽水混凝土擴散分析模型求解的氯離子分布曲線的一致性。將對流區Δx深度處對應的氯離子濃度值Cs,Δx作為邊界條件引入飽水模型中，采用上述6組試驗時長，基于Fick定律進行常規擴散方程求解，將各組計算結果與修正氯離子分布曲線分別進行對比，如圖8所示。可以發現在混凝土服役的各個時期，二者都具有良好的相似性和規律的一致性，更好地驗證了本文提出計算Δx改進方法的可行性。說明只要能夠得到對流區深度Δx，就可以借助擴散方程公式(8)將干濕循環作用下混凝土內部氯離子傳輸問題簡化為常規的氯離子擴散方程的求解，從而將對流擴散耦合問題簡化為常規的擴散問題。因此，簡化問題的核心就在于確定對流區深度。

圖8 基于Fick定律的氯離子分布曲線和修正氯離子分布曲線對比結果Fig.8 Comparison results of chloride ion distribution curves based on Fick’s law and modified model

3 對流區深度的確定及影響參數分析

對流區的形成是氯離子對流擴散耦合作用的結果，其深度必然受到外界多個因素的影響。根據前述分析和沿海結構實際使用特性，本文篩選了服役時間、日平均氣溫和干燥濕潤時間比等參數，分析討論對流擴散區深度Δx值的變化規律,提出了假定對流區深度擬合公式：

Δx=ηT·ηφ·Δx0

(9)

式中：Δx0為對流區深度基準值；ηT為溫度修正參數；ηφ為干濕時間比修正參數。

3.1 服役時間影響

本文在研究服役時間對Δx的影響時，首先考慮單次循環時長分別為2 d、3 d和4 d時，保持其他計算參數不變的情況下取干燥濕潤時間比φ=1.0，計算得到服役20年后混凝土結構內部氯離子分布狀況，如圖9所示。觀察發現2 d、3 d和4 d不同條件下的計算結果差異很小，故可認為單次循環時長這個參數對于氯離子傳輸過程的影響不顯著。因此，在后續研究中可以忽略該參數變化所帶來的影響。

(10)

圖9 不同單次循環時間計算結果Fig.9 Calculation results of different single cycle time

圖10 Δx關于時間的擬合結果Fig.10 Fitting results of Δx for time

3.2 溫度場影響

為了研究溫度場對對流區深度的影響，本文計算了Tav分別為285.15 K、295.15 K、305.15 K和Tam分別為5 K和10 K時這6種溫度條件下服役300 d后混凝土內部氯離子分布的狀況，如圖11所示。分析結果表明氣溫日變化幅值Tam這個參數對于整個氯離子侵蝕過程的影響并不顯著，在后面的計算研究過程中將不考慮該因素的變化。

干燥濕潤時間比φ=1.0不變的情況下，在計算中統一選取溫度變化幅值Tam=10 K，僅考慮日平均氣溫的變化，溫度計算工況見表3。

分別計算上述各溫度工況下6組不同使用時長(分別為30 d、180 d、360 d、1 800 d、3 600 d、7 200 d)對應的不同服役期對流區深度，整理上述6個工況的計算結果，同時以Δx0為基準，擬合得到以日平均氣溫Tav和服役時間t為自變量的溫度修正參數ηT公式，擬合情況如圖12所示，擬合優度R2=0.85，擬合效果滿足工程需求。

(11)

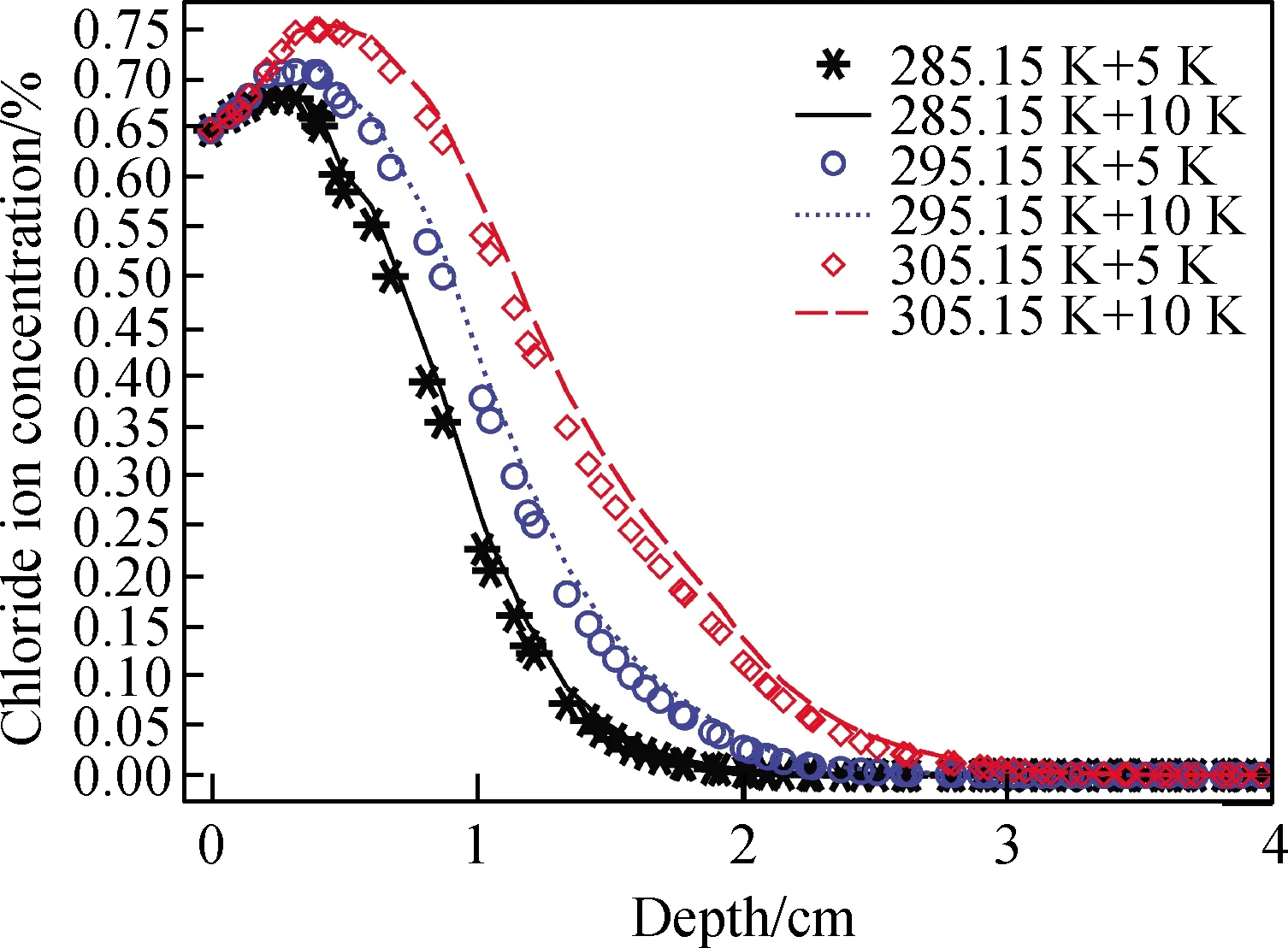
圖11 不同溫度條件計算結果Fig.11 Calculation results under different temperature conditions

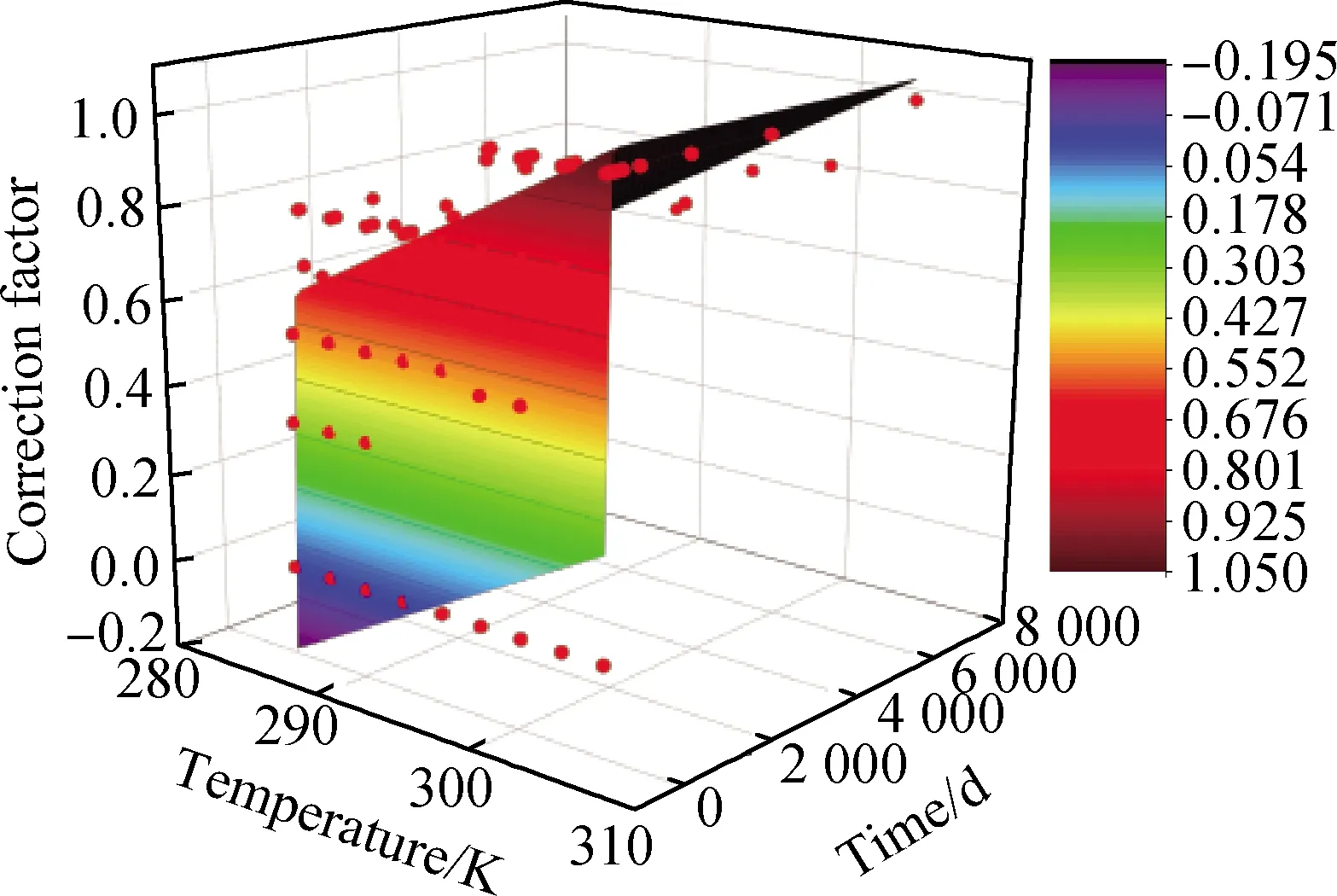
圖12 溫度修正參數擬合情況Fig.12 Fitting of temperature correction parameters

3.3 干燥濕潤時間比影響

(12)

綜上所述，將公式(10)～(12)代入公式(9)中即可確定對流區深度的預測值。該計算模型主要考慮了服役時間、日平均氣溫和干燥濕潤時間比等參數，將單次循環時長和氣溫日變化幅值這兩個影響較小的參數剔除。

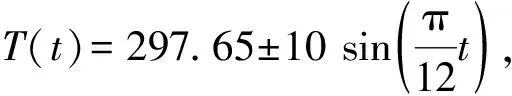
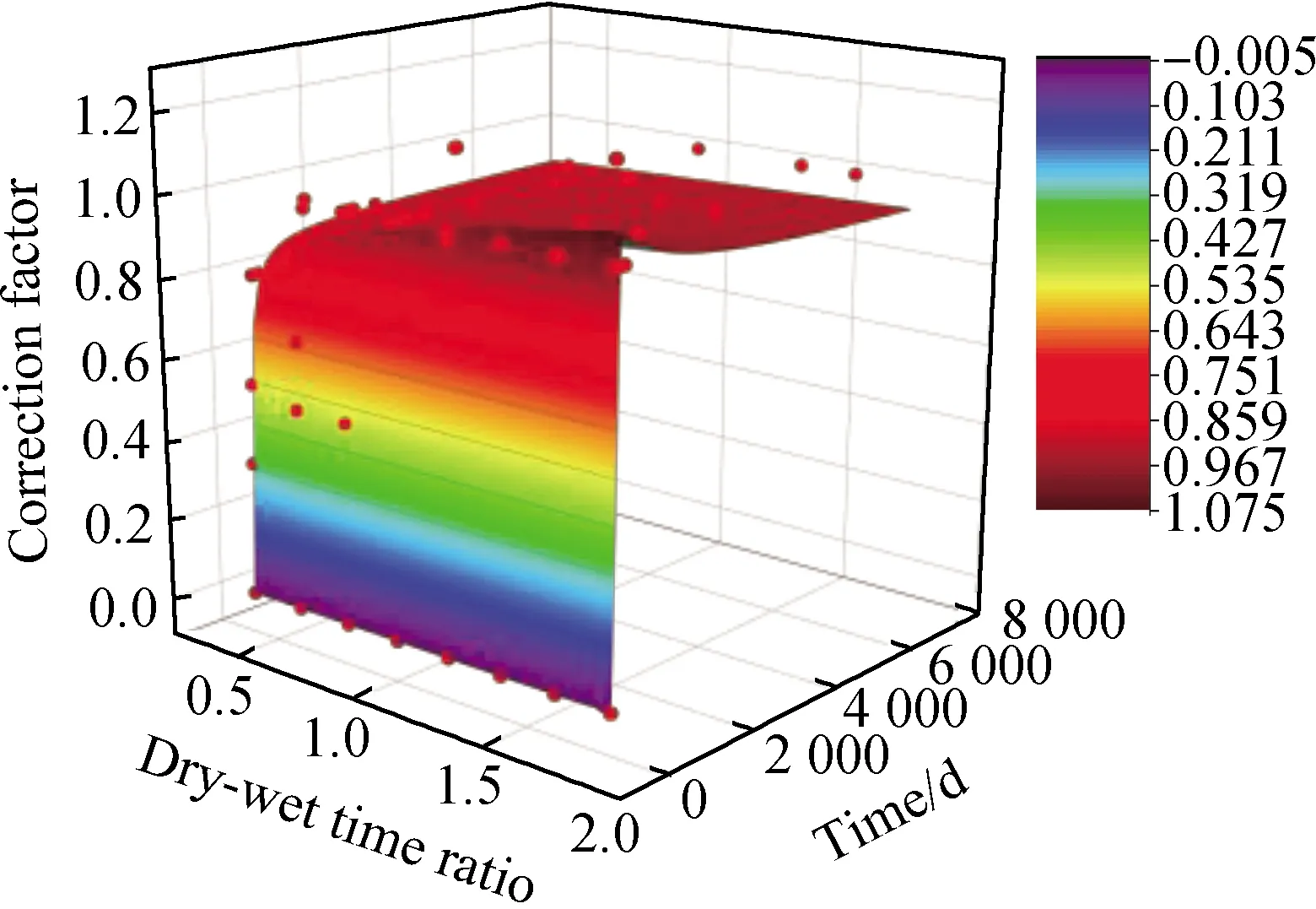
圖13 干濕時間比修正參數擬合情況Fig.13 Fitting of modified parameters of dry-wet time ratio

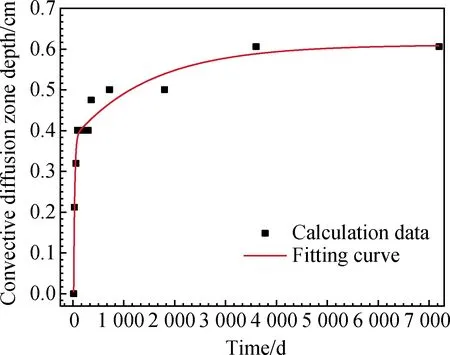
圖14 校核計算結果Fig.14 Checking calculation results

4 結 論

針對干濕交替環境下混凝土內部的氯離子傳輸受到對流與擴散耦合作用，本文給出了非飽和混凝土內部氯離子傳輸計算模型和分析方法，該方法可以方便地將對流與擴散耦合問題解耦為含有對流區深度Δx的常規擴散方程，并進一步給出了對流區深度Δx的擬合公式，為準確預測干濕交替環境中的氯離子傳輸規律、簡化計算模型提供了解決的思路和方法，具體的研究結論如下：

(1)以混凝土細觀尺度分析模型為基礎，引入環境溫度場變化、水分遷移和氯離子傳輸等因素建立了干濕交替區域氯離子傳輸數值計算模型，通過試驗數據對表層氯離子分布特征、累積峰值深度及混凝土全區域氯離子分布規律的分析對比，證實本計算模型的準確性和有效性，說明該類綜合了溫度場、水分遷移與氯離子傳輸的混凝土細觀數值模型可以精確地描述干濕交替環境下混凝土內部氯離子的傳輸機制和行為。

(2)通過對干濕交替環境下混凝土內部氯離子的運移機制與傳輸行為的分析，證明了對流區深度Δx的存在，并有效地將氯離子擴散曲線整體解耦為對流區部分及其后的擴散區部分，為此類問題的簡化提供了求解思路。

(3)針對流區深度Δx，剔除低影響因子后，以計算服役時間、日平均氣溫和干濕時間比為主要影響因子給出了對流區深度Δx擬合公式Δx=ηT·ηφ·Δx0，并驗證了該公式的適用性及準確性。

上述結論可為處于干濕交替環境中的混凝土結構氯離子傳輸問題的計算提供簡化而較為準確的方法，為沿海混凝土結構內部氯離子的傳輸作用機理和分布狀態研究提供參考。但是，本文的研究內容對環境溫度場的變化考慮較為簡化，未引入大體積混凝土內部溫度梯度的影響；同時尚未驗證在自然降雨環境中模型的適用性，后續將通過深入了解環境條件變化情況進一步展開研究。