基于CEEMD和GWO-SVR的銑削振動信號前瞻預測

吳 石, 張軒瑞, 劉獻禮

(哈爾濱理工大學 先進制造智能化技術教育部重點實驗室,哈爾濱 150080)

汽車車身構件日益復雜，相應淬硬鋼模具存在大量的凸凹、溝槽等結構，為克服模具加工制造和裝配中存在的這種結構性困難，多采用鑲塊式拼接模件。在模具整體銑削加工過程中，由于在拼接處存在硬度差，銑削振動變化大，產生的沖擊振動會在短期內導致刀具磨損加劇，模具表面加工質量下降等。如果能準確地預測模具拼接區的銑削振動趨勢，通過快速改變銑削參數進行前瞻控制，有利于在拼接處減小銑削力的瞬時突變，減少沖擊振動對模具加工精度和產品質量的影響[1]。

在拼接模具整體銑削加工過程中，由于加工工況和切削環境復雜，測得的銑削振動信號中存在干擾信息和較強的非平穩特征[2]，這些干擾信息的存在會嚴重影響銑削振動信號預測的精準度，因此需要對振動數據進行預處理以提高振動信號前瞻預測的準確性。

目前時頻分析方法是分析非平穩和非線性信號的最常用的方法，如小波分析法、Hilbert-Huang變換等[3]。小波變換應用過程具有局限性，其基函數和分解層數的選取缺乏自適應性[4]。經驗模態分解(empirial mode decomposition,EMD)方法是一種瞬時信號處理方法，避免了選取小波基函數的弊端，能夠實現非平穩信號的分解并濾除噪聲干擾，EMD方法以Hilbert變換為基礎，將瞬時頻域具有物理意義的信號定義為固有模態函數(intrinsic mode function, IMF)，在非平穩信號處理領域得到應用[5-6]。由于EMD分解方法存在模態混疊現象，因此Wu和Huang提出了集合經驗模態分方法(emsemble empirial mode decomposition, EEMD)，有效地抑制了信號分解過程中局部極值在短時間內的頻繁跳動[7]。

銑削振動信號預測常采用線性時間序列的預測方法[8-11]，但在實際切削環境中，機床、刀具和工件使銑削呈現典型的非線性特征，因此銑削振動信號的非線性時間序列預測方法得到了迅速發展[12]。對于非線性時間序列預測，人工神經網絡(artificial neuron network, ANN)的特殊性在于其本身處理數據時具有自學習能力，而且對于非線性數據的預測能力強，然而ANN算法在操作中會出現一些問題[13]，如收斂速度慢、難以確定網絡結構和局部最優等。支持向量機[14]是一種基于統計學習理論的學習算法，它的優勢主要是在小樣本、少信息、非線性及高維空間模式識別中，克服了人工神經網絡極易陷于局部極小和過度擬合的問題[15]，而且對于小樣本數據分析來說，支持向量機擁有良好的學習能力和推廣能力,被廣泛應用于銑削顫振識別[16-17]、粗糙度預測[18]和銑削力預測[19]中，已經成為研究者用于解決非線性時間序列預測的一種重要工具。

本文提出了一種基于互補式集成經驗模態分解方法和支持向量機回歸結合灰狼群算法的振動信號預測模型(CEEMD-GWO-SVR模型),一方面通過加入正負白噪聲的方式減少模態混疊對于振動信號EMD分解的影響，提高模態分量的平穩性；另一方面基于修正的GWO算法尋找支持向量回歸機參數的最優解，總體上提高拼接處銑削振動信號預測的精準度。

1 模具拼接縫銑削振動信號的CEEMD分解

1.1 模具拼接區銑削試驗

若要進行拼接區銑削信號的CEEMD分解和前瞻預測試驗，需采集真實的銑削振動信號進行后續的試驗。

銑削試驗布置如圖1所示，試驗用的機床為 VDL-1000E型三軸立式加工中心，刀具為戴杰二刃整體硬質合金球頭立銑刀(DV-OCSB2100-L140)；工件材料為淬硬狀態下模具鋼(Cr12MoV)，工件尺寸為200 mm×200 mm×60 mm，分成3個鑲塊，硬度分別通過不同的熱處理工藝調至45HRC、50HRC、45HRC，通過2根長度為200 mm的不銹鋼高強度鉸制孔用螺栓連接為一個整體，拼接縫隙為0.2 mm。曲面淬硬鋼模具銑削采用小切深，小行距和小進給的切削參數，加工參數如表1所示。

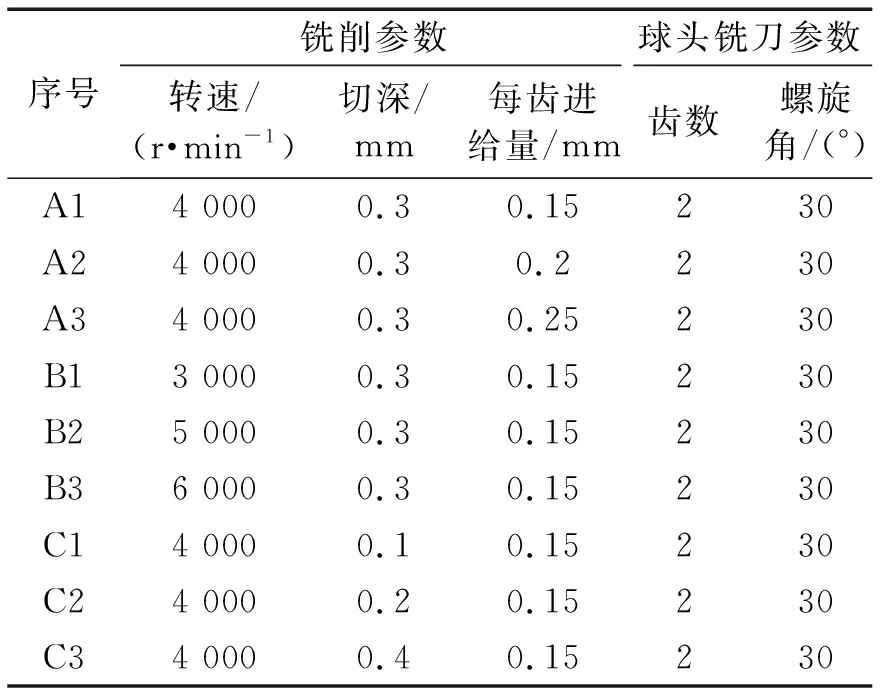
表1 試驗用刀具參數及切削用量Tab.1 Test tool parameters and cutting parameters

銑削試驗時，從硬度為45 HRC的鑲塊向硬度為50 HRC的鑲塊進行銑削加工，銑削采用順銑切削，共計完成9組試驗。每組試驗時均通過加速度傳感器、數據采集系統測試工件的X、Y、Z三個分量上的振動加速度信號，采集到的銑削振動信號為動態銑削力和過縫沖擊力共同激勵后產生；由于Z向系統剛度較大，銑削振動信號幅值較小；X、Y兩個方向的銑削振動信號幅值較大，進給方向(機床Y方向)最大，因此本文分析銑削振動信號波形時只提取X、Y兩個方向的試驗數據對其進行分析，過試驗模具拼接縫后的銑削振動信號如圖2所示。如圖2所示的銑削振動信號為主軸轉速n=4 000 r/min、每齒進給量fz=0.15 mm/z、徑向切深分別為ae=0.1 mm、ae=0.2 mm、ae=0.3 mm和ae=0.4 mm時的四組銑削振動加速度試驗數據，數據時序為銑削試驗過程中的39.43～39.73 s。

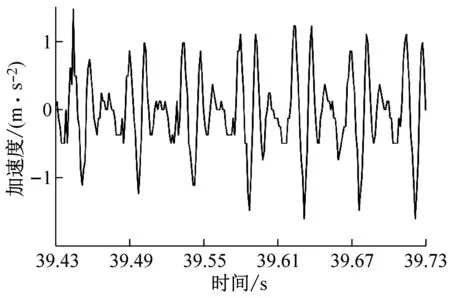
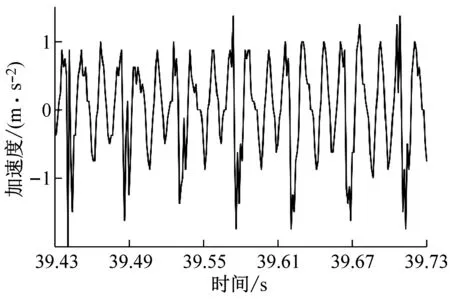
(a) ae=0.1 mm時工件X、Y兩個方向加速度信號試驗數據

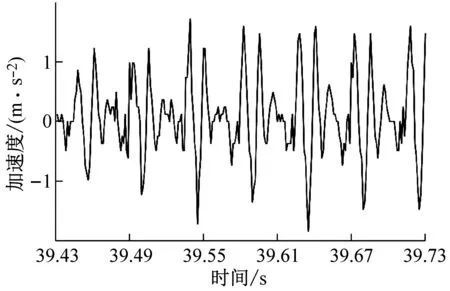
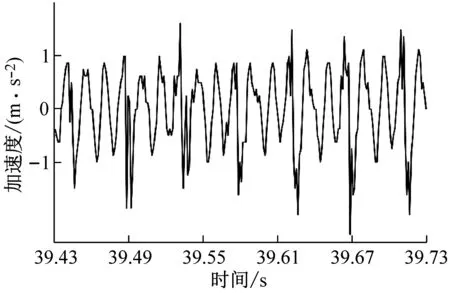
(b) ae=0.2 mm時工件X、Y兩個方向加速度信號試驗數據

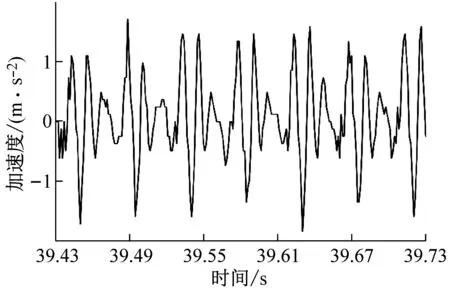
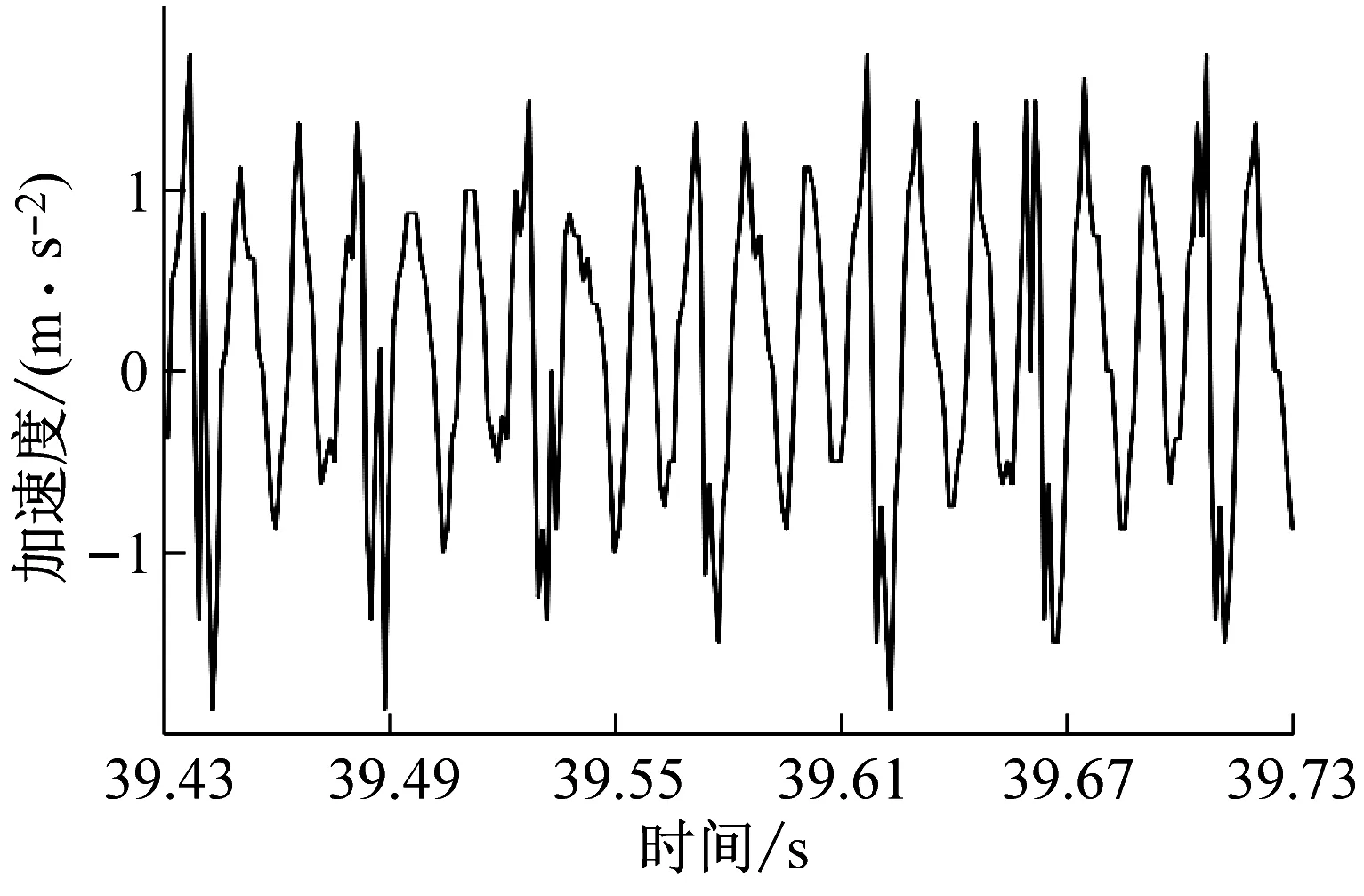
(c) ae=0.3 mm時工件X、Y兩個方向加速度信號試驗數據

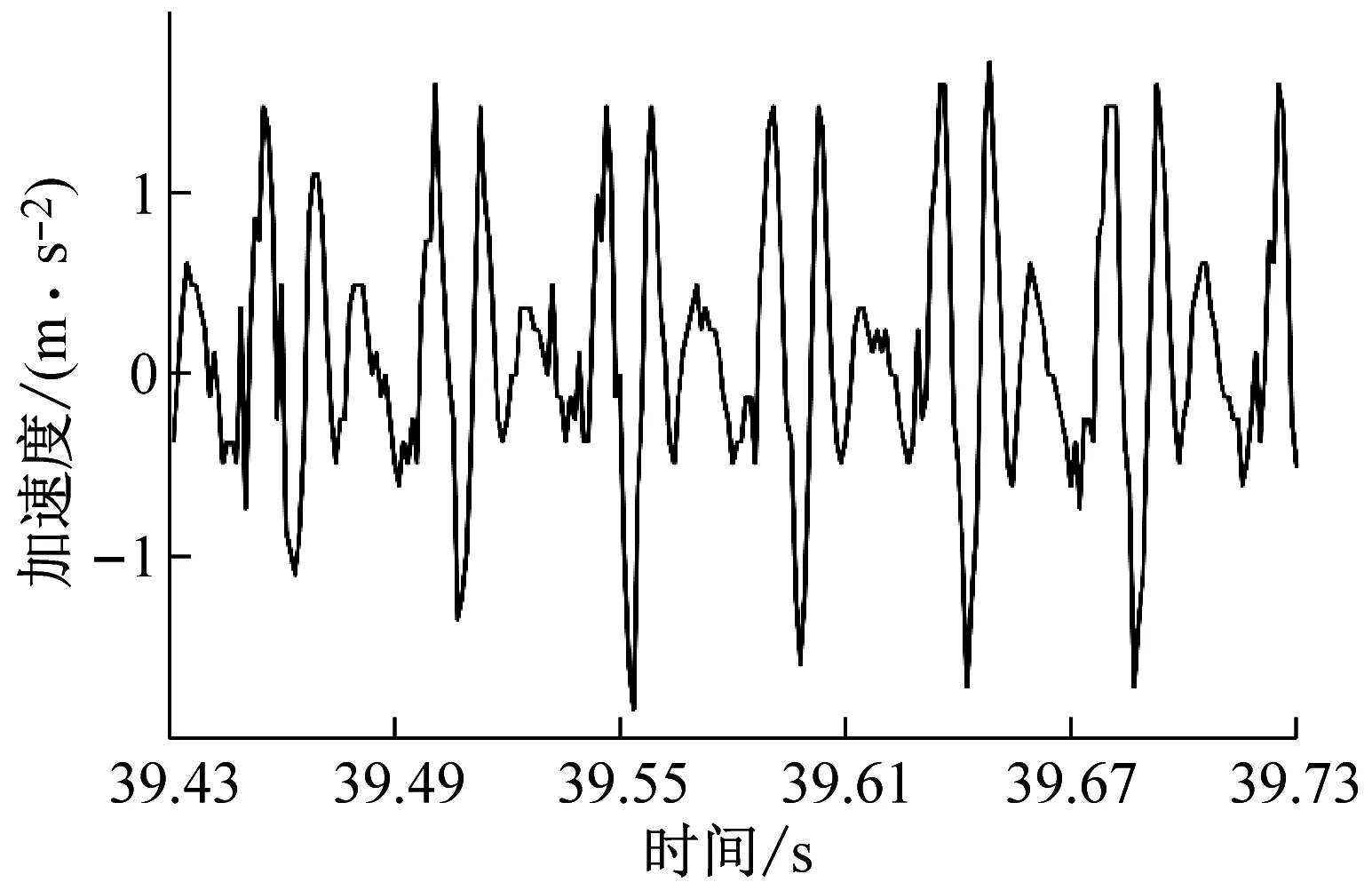
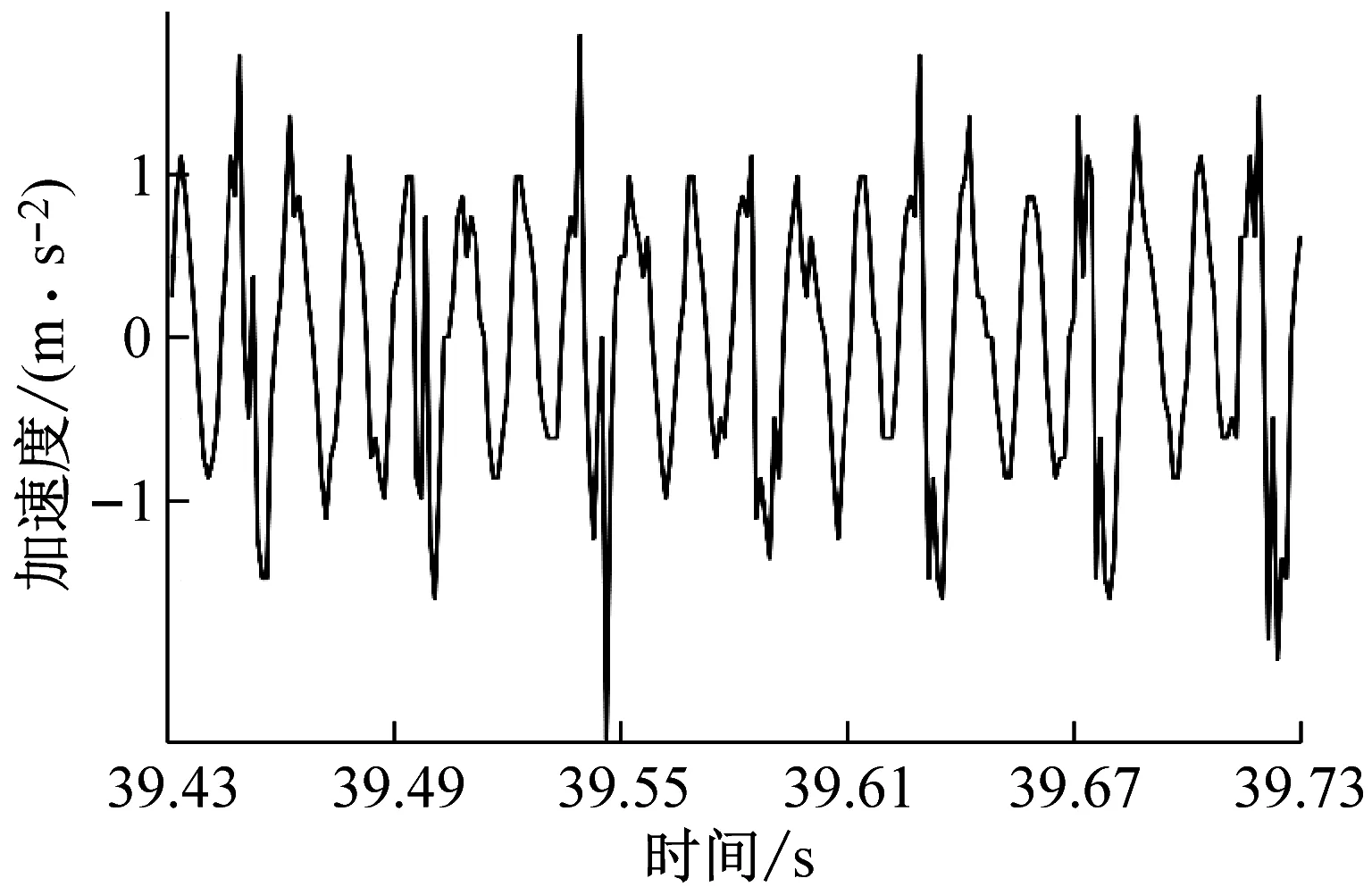
(d) ae=0.4 mm時工件X、Y兩個方向加速度信號試驗數據圖2 不同變切深下的振動加速度信號圖Fig.2 Vibration acceleration signal diagram under different variable depths of cut

1.2 基于CEEMD的銑削振動信號分解

過拼接縫后的銑削振動信號中存在有干擾信息，同時在銑削加工過程中的振動信號具有較強的非平穩特征，這些干擾信息對準確預測拼接縫振動信號會產生較大影響，所以需要對數據進行預處理。

EMD算法是一種自適應式時頻域信號分解方法，相對于傳統信號分解模型，EMD展現出了適應強的特性，EMD將一組信號分解成了若干個固有模態分量和一個殘余項，公式如下

(1)

式中:x(t)是原始信號；m是IMF個數；ci(t)是第i個IMF分量；rm(t)是殘余項。

但是EMD算法存在模態混疊問題，針對模態混疊問題，出現了EEMD算法來解決模態混疊問題，EEMD算法是在EMD分解的每一步驟中分別加入等幅的白噪聲，但加入的白噪聲會產生信息干擾，Yeh等[20]提出了CEEMD算法,CEEMD算法在信號中加入了N對相反噪聲，然后分解加入噪聲的新信號，最后得到不同的IMF分量，從而進行分解，如圖3所示。CEEMD算法具體步驟如下

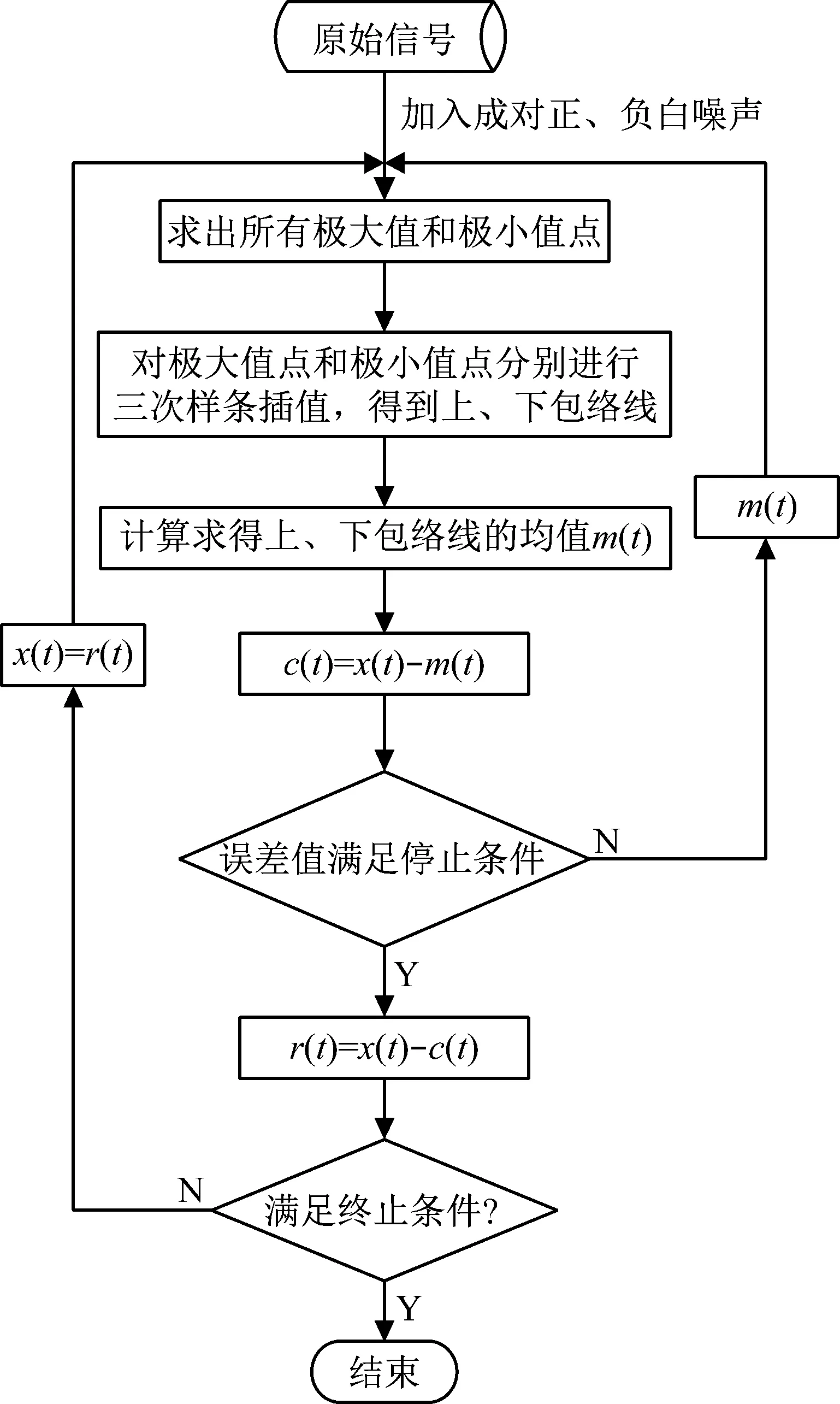
圖3 CEEMD原理流程圖Fig.3 Flow chart of CEEMD working principle

(1) 將一組符號相反的噪聲加入到目標信號中，每組噪聲的幅值相同，然后產生一對新信號

(2)

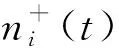
(2) 分解新信號，得到兩組含有白噪聲的信號分量IMF1和IMF2，且這兩組分量正負互補。

(3) 將兩組信號的IMF分量進行整合得到最終的IMF分量。

對加速度信號進行CEEMD分解之前，為了避免試驗數據出現飽和現象，對試驗數據進行歸一化處理，使其樣本數值處于[0,1]之間。

為了獲得前瞻預測試驗中所需輸入源信號，對銑削振動加速度信號進行CEEMD分解，得到5個頻域穩定的固有模態分量IMF1-IMF5和一個剩余分量Res的波形圖，不同工況下的CEEMD分解如圖4所示。

從圖4中可以看出，分解后IMF分量圖與處理前的銑削振動加速度信號相比，IMF分量圖的波動變化較為平穩，頻譜特征由分量從高頻到低頻依次表征出來。該方法將原有不平穩的銑削振動加速度信號分解成了多個平穩子序列，保存了處理前的信號特征，又可以將平穩的信號序列輸入到支持向量機中，能夠最大程度上學習和訓練數據集。

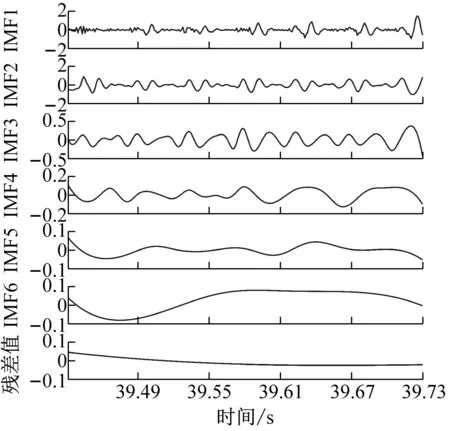
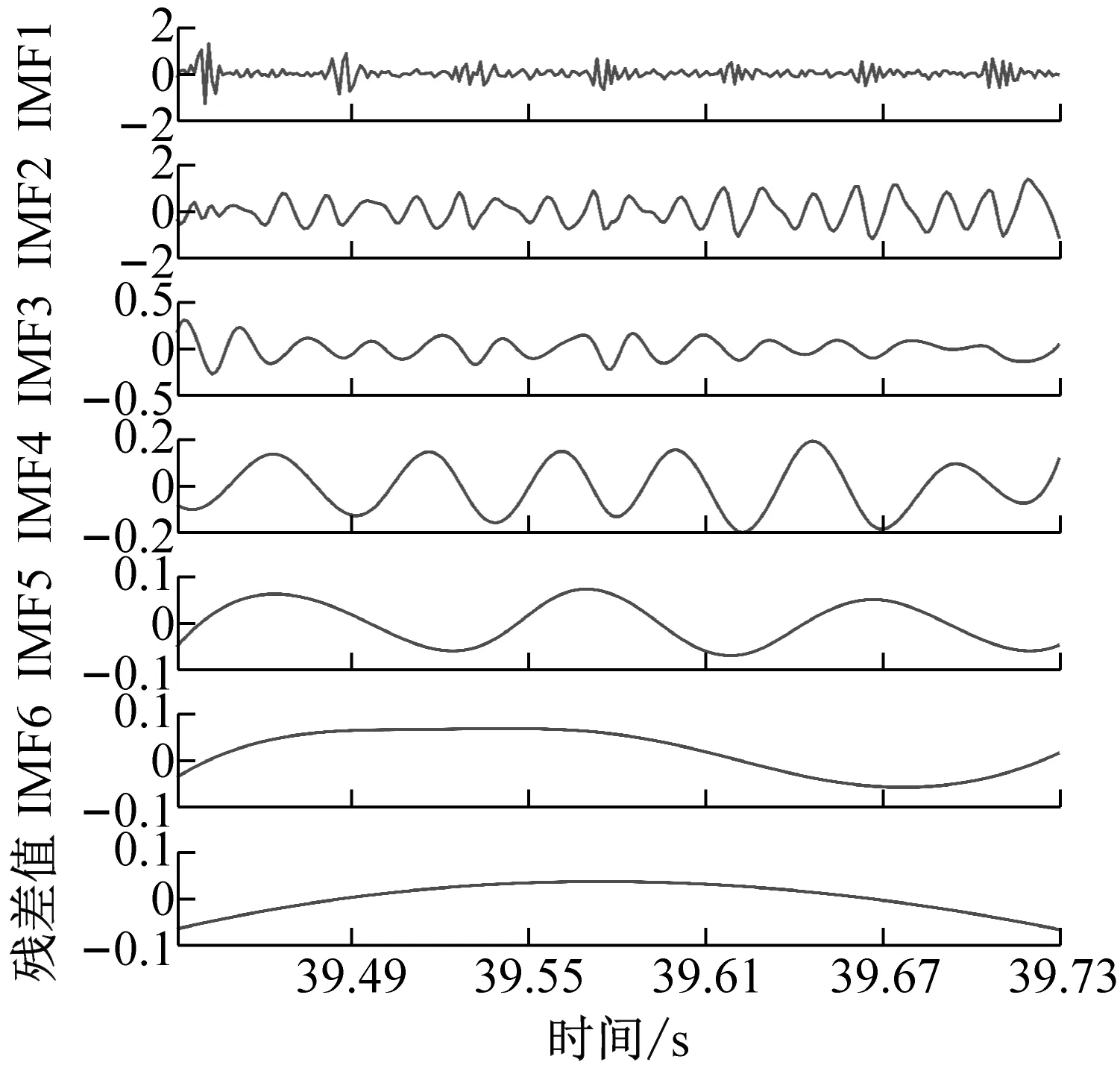
(a) ae=0.1 mm時工件X、Y兩個方向加速度信號CEEMD分解圖

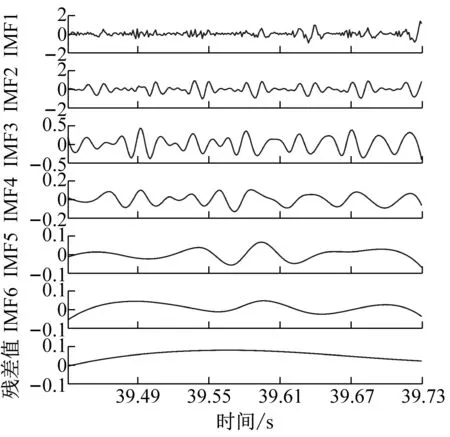
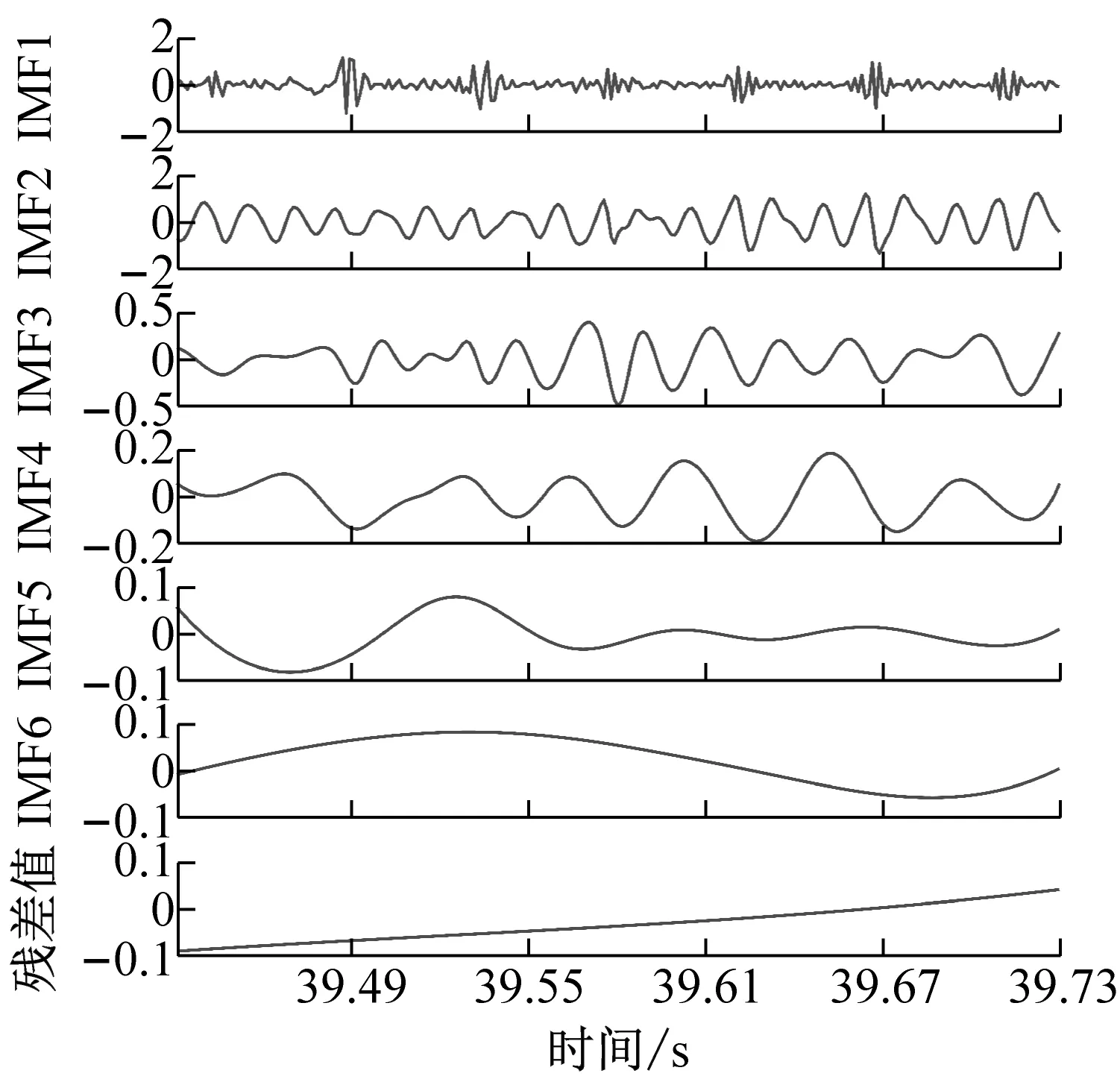
(b) ae=0.2 mm時工件X、Y兩個方向加速度信號CEEMD分解圖

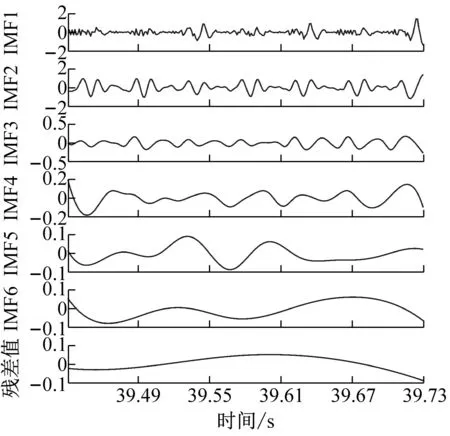
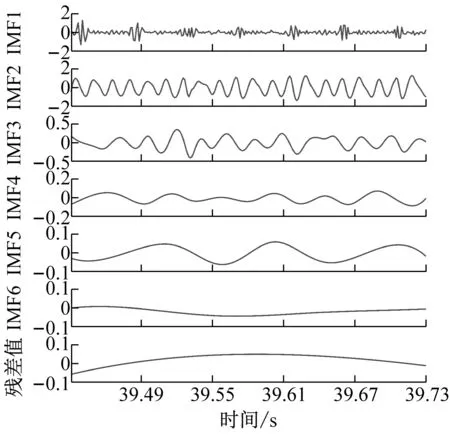
(c) ae=0.3 mm時工件X、Y兩個方向加速度信號CEEMD分解圖

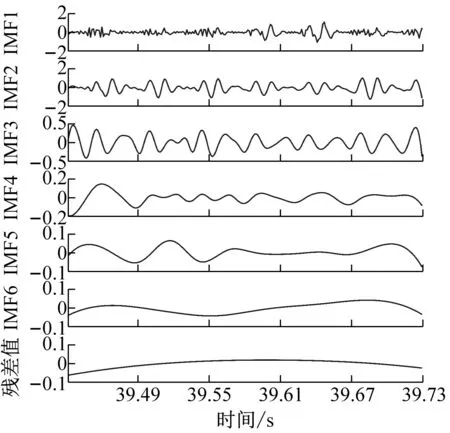
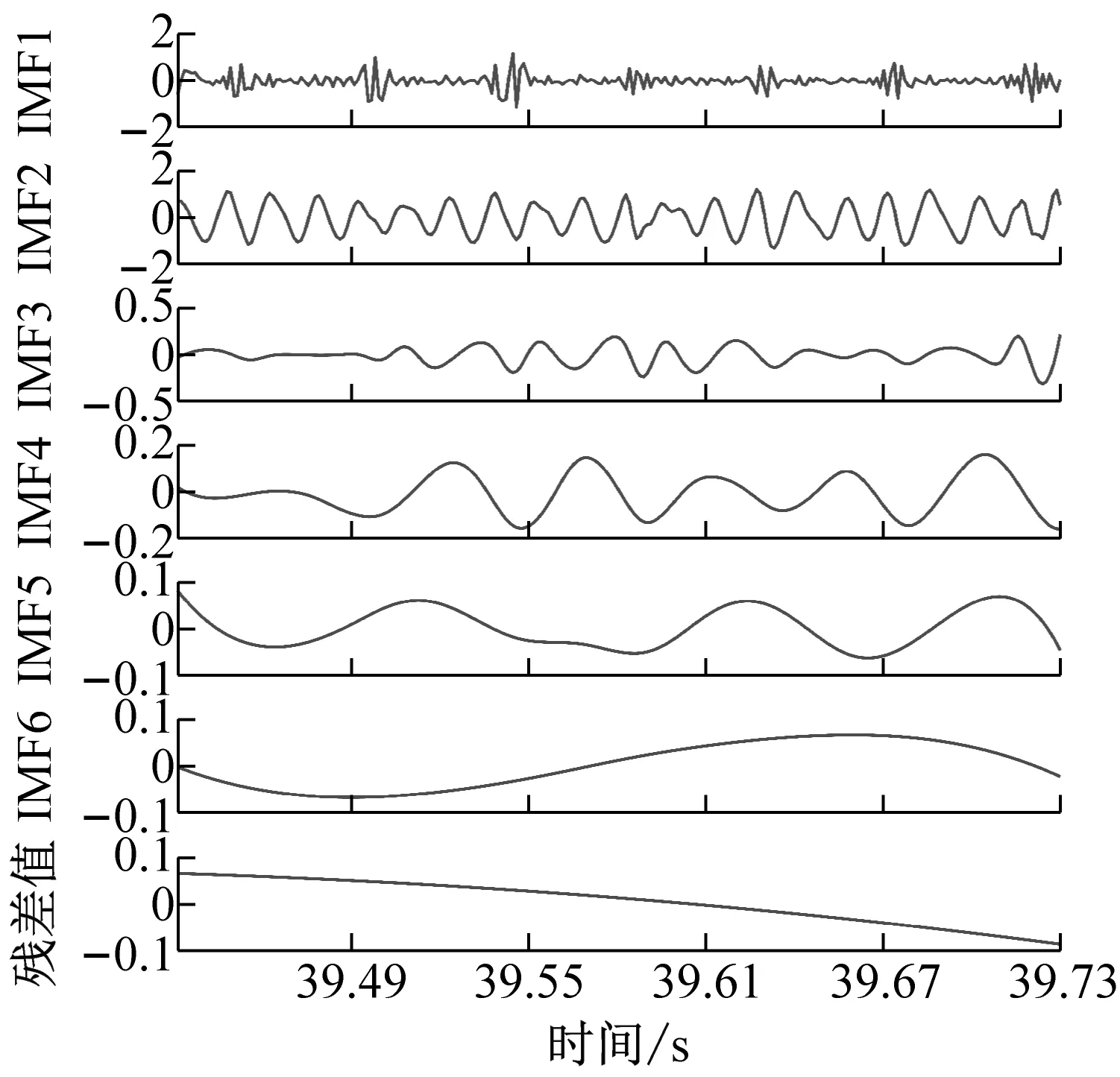
(d) ae=0.4 mm時工件X、Y兩個方向加速度信號CEEMD分解圖圖4 不同變切深下的振動數據CEEMD分解圖Fig.4 CEEMD decomposition diagram of vibration data under different variable depths of cut

2 支持向量機回歸方法

基于支持向量機的數據回歸算法與分類算法相似，都是以結構風險最小化原則進行求解。本文基于改進的支持向量回歸方法預測銑削振動數據的發展趨勢。支持向量回歸(support vertor regression，SVR)，它對非線性時間序列的預測較穩定，首先通過非線性函數變換φ(xi)，把數據xi映射到高維特征空間，繼而在高維特征空間里面，找到一個能夠準確地表明輸出數據及輸入數據存在關系的函數f(xi)，即SVR函數

f(x)=wTφ(x)+b,φ:Rn→F,w∈F

(3)

為了使實際風險達到最小的效果，根據結構風險最小化原理，優化的結構風險目標函數為

(4)

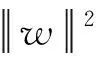
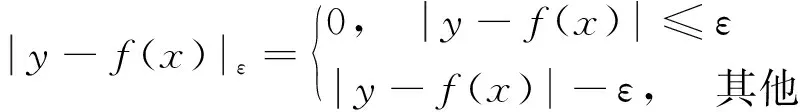
(5)

SVR即為式(4)的優化問題的求解公式

-yi+wTΦ(x)+b≤ε+ξi

(6)

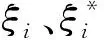
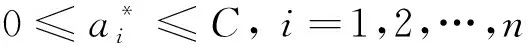
(7)

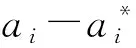
(8)

利用KKT(Karush-Kuhn-Tucker)條件計算出偏差b

(9)

最后得到回歸函數f(x)的表達式

(10)

式中，K(xi,x)=Φ(xi)Φ(x)為一個滿足Mercer條件的核函數。此函數可以越過具體形式從而達到非線性變換的非線性化操作，這是SVR的一個顯著特點。目前SVR核函數中使用最多的是帶有寬度為σ的徑向基核函數(RBF核函數)，使用徑向基核函數的SVR預測模型的預測效果要優于使用其它核函數預測模型[21]，徑向基核函數為

exp(-1xi-x12/2σ2)]+b

(11)

3 改進的GWO-SVR預測模型

3.1 灰狼優化算法

灰狼優化算法(gray wolf optimization, GWO)是由澳大利亞學者Mirjalili等[22]提出來的一種群智能優化算法，該算法受到了灰狼捕食獵物活動的啟發，它具有收斂性能強、參數少、易實現等特點。

灰狼隸屬于群居生活的犬科動物，且處于食物鏈的頂層。灰狼遵守著一個社會支配等級關系，群組織為金字塔結構，最頂層為α狼，具有領導地位；第2層β狼屬于從屬狼，可以作為α狼的候選者；第3層是δ狼，地位次β狼；最底層ω狼是所有狼群的基礎。

灰狼群狩獵過程分為以下幾個階段：

(1) 追蹤獵物

灰狼在狩獵過程中圍繞獵物，將其行為做出以下定義

(12)

(13)

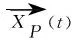
(14)

(15)

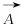
(2)包圍獵物

灰狼有識別獵物的強能力，且α狼可以領導灰狼包圍獵物，但在獵物(最優解)位置未知的情況下。為了模擬灰狼捕獵行為，假定α狼、β狼和δ狼了解獵物的潛在位置，保存三個最佳解決方案，并且要求其他灰狼(ω狼)作為搜索代理，根據最佳解決方案進行灰狼位置的迭代更新，公式為

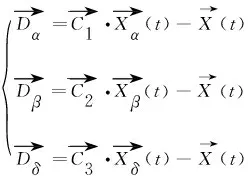
(16)

(17)

(18)

式(17)代表ω狼朝三個潛在解α狼、β狼和δ狼的步長和方向；公式(18)代表ω狼的最終位置。

(3) 攻擊獵物

(4) 尋找獵物

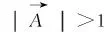
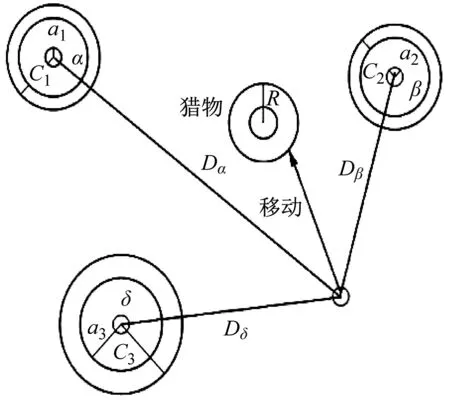
圖5 狼群圍捕獵物位置更新圖Fig.5 An updated map of the location of wolves hunting prey

3.2 GWO-SVR模型

本文建立了基于灰狼算法優化支持向量機(GWO-SVR)的銑削振動信號預測模型，灰狼算法優化SVR過程如圖6所示。該模型主要是使用GWO算法優化SVR的懲罰系數C和核函數參數g(徑向基核函數參數帶寬σ)，通過選擇全局最優參數來提高SVR的預測精準度和預測速度。同時選取了傳統常見的GA算法和PSO算法進行對比，分析三種尋優算法的優劣。

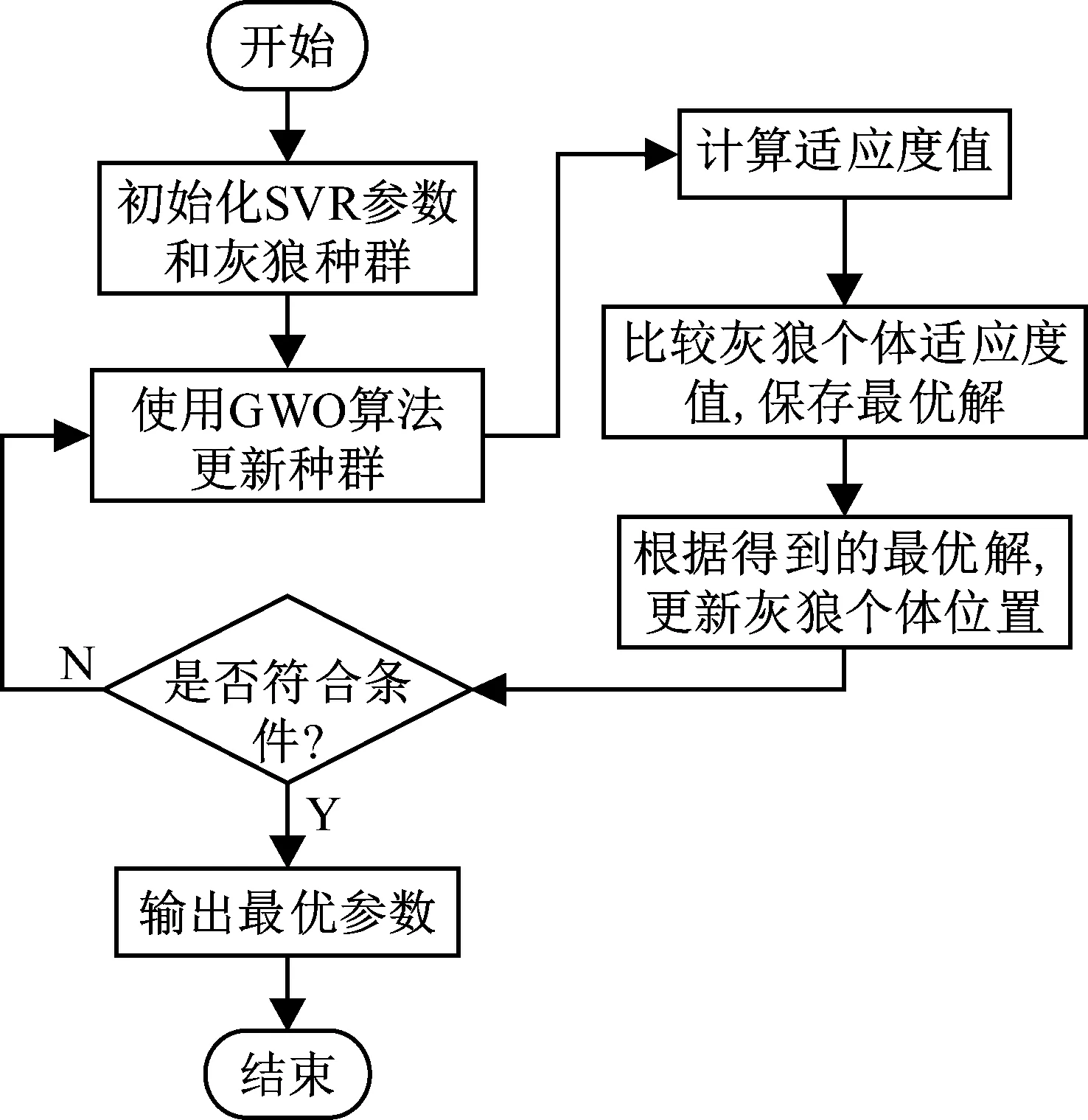
圖6 灰狼優化算法流程圖Fig.6 Flow chart of gray wolf optimization algorithm

4 試驗測試及結果分析

本文首先對模具樣件拼接縫中測得的銑削振動信號數據進行CEEMD分解，得到各個分量序列和殘余項，然后基于GWO-SVR預測模型對每個分量進行訓練和預測，訓練和預測時基于GWO算法對SVR的參數C和g進行全局尋優，將各個分量的預測結果相加得到短期銑削振動總預測結果，預測模型如圖7所示。

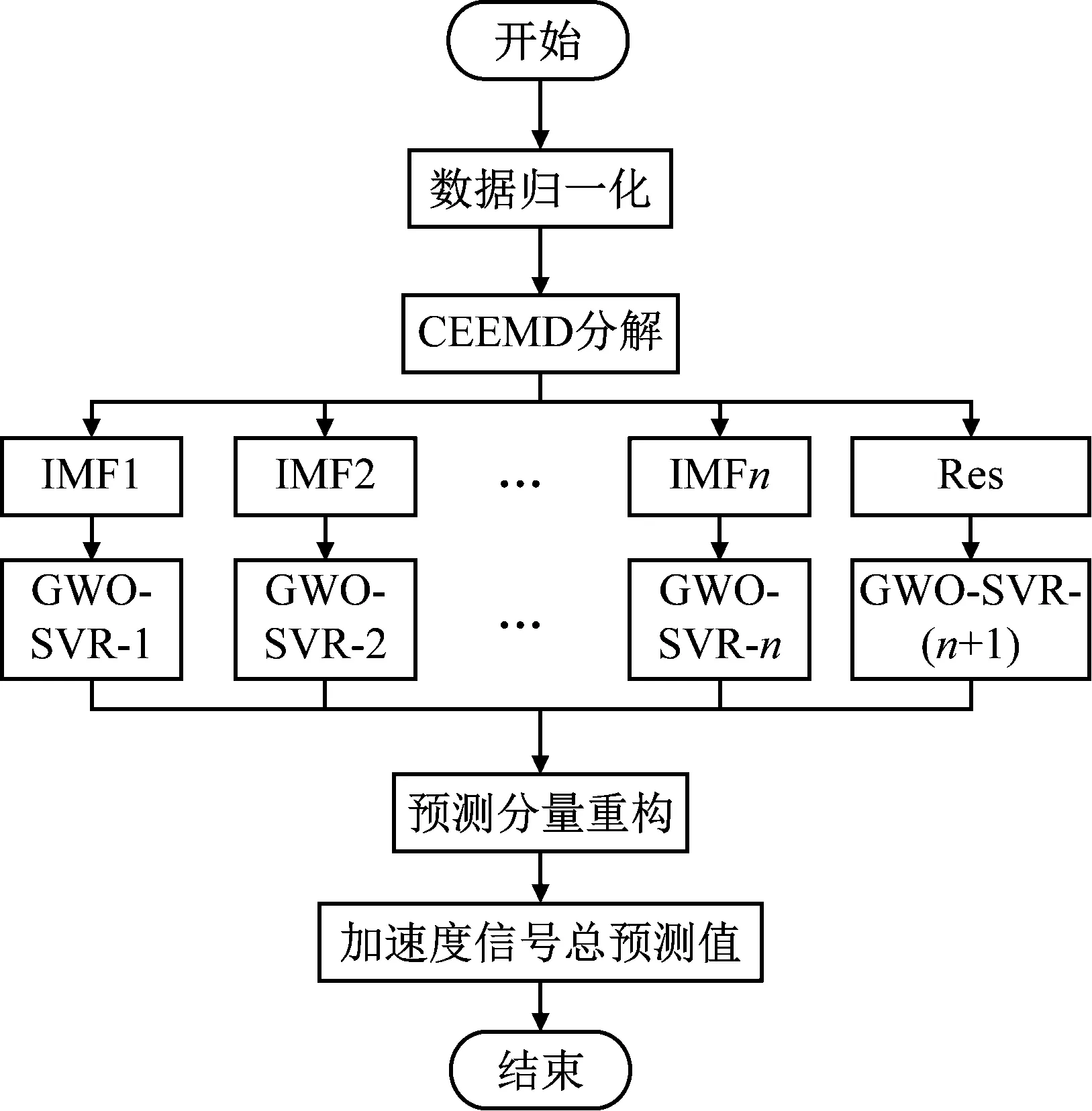
圖7 CEEMD-GWO-SVR預測方法Fig.7 CEEMD-GWO-SVR prediction method

基于GWO對SVR中的參數C、g進行參數尋優過程中，首先進行初始化：種群規模N=20，最大迭代次數為200，C和g的范圍從0.01～100。銑削振動加速度值被作為預測值輸出，算法被用于訓練模型時，GWO、PSO和GA三種尋優算法的適應度如圖8所示。

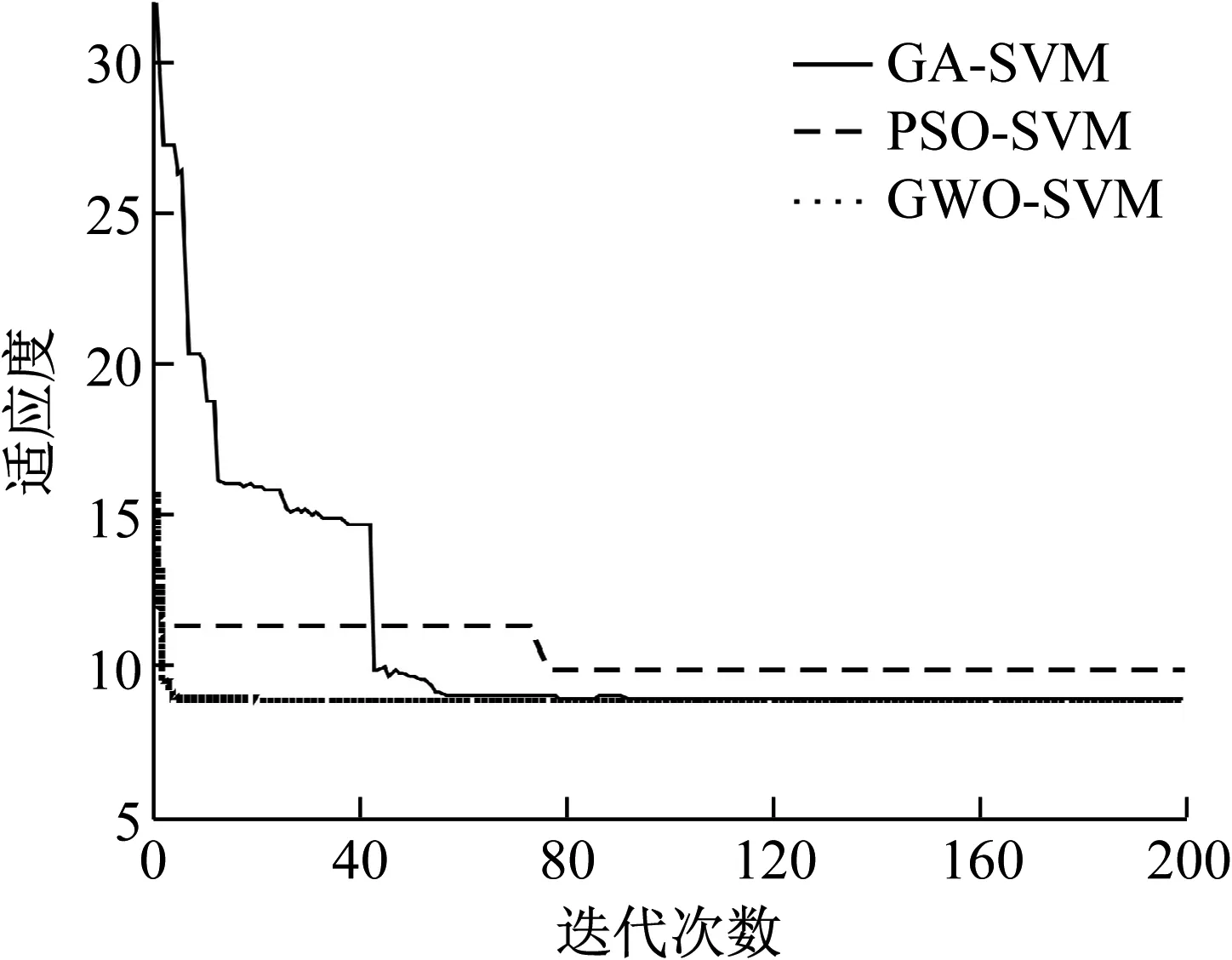
圖8 不同算法的適應度函數曲線Fig.8 Fitness function curves of different algorithms

三種算法對于適應度函數的計算不同，所以將會產生各自算法的全局最優參數，進而基于不同算法的支持向量機回歸預測的精度也有所不同，不同尋優算法的最優參數尋優結果如表2所示。

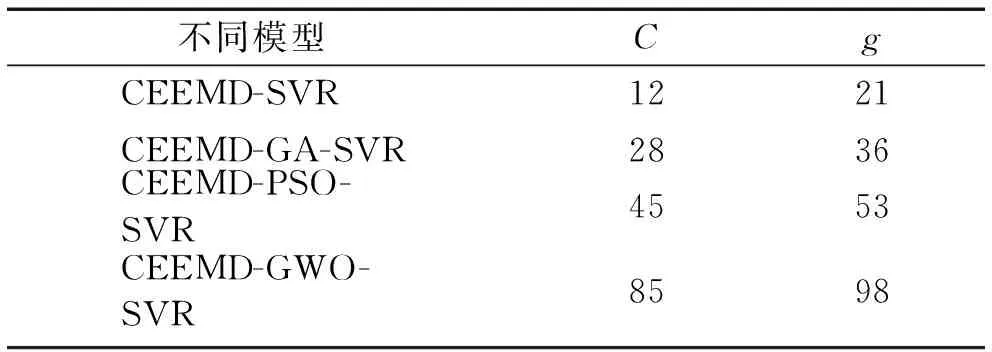
表2 不同方法參數尋優表Tab.2 Parameters optimization table of different methods

圖8中可以看出，PSO算法在迭代次數達到第78次左右適應度函數完全收斂得到最優性能，其收斂性較差；而GA算法和GWO算法尋優速度和收斂性均大于PSO算法，其中GA算法在迭代次數為第50次時適應度函數趨于收斂，GWO算法則是在迭代次數為第5次時適應度函數完全收斂，可以看出GWO算法在尋優速度和收斂性方面性能優越，最終得到的全局最優懲罰因子C=76，全局最優核函數參數g=88。

建立SVR滾動預測模型，使SVR預測模型充分學習數據集內的數據規律，本文采用銑削振動信號中的第1～100時序數據點預測第101點，用第2～101時序數據點預測第102點，輸入記為X，輸出記為Y，一個X和Y記為一組樣本，共計753組；前452組樣本構建為訓練集(占總樣本數的60%)，后301組樣本構建為測試集(占總樣本數的40%)。訓練集是預測模型用來訓練數據規律的數據集，當預測模型訓練完成過后得到數據集的變化規律，然后預測模型根據預測集的步長預測步長相對的數據，得到一段模型預測后的數據，最后把預測數據和訓練集的真實數據進行圖形對比。

對經過CEEMD算法分解得到的加速度信號(IMFs信號)通過GWO-SVR預測模型進行預測，并將預測曲線進行反歸一化處理；然后將各個經過反歸一化處理后的預測曲線進行預測信號結果重構，得到振動加速度總信號(IMFs信號)的預測曲線，預測曲線如圖9所示。

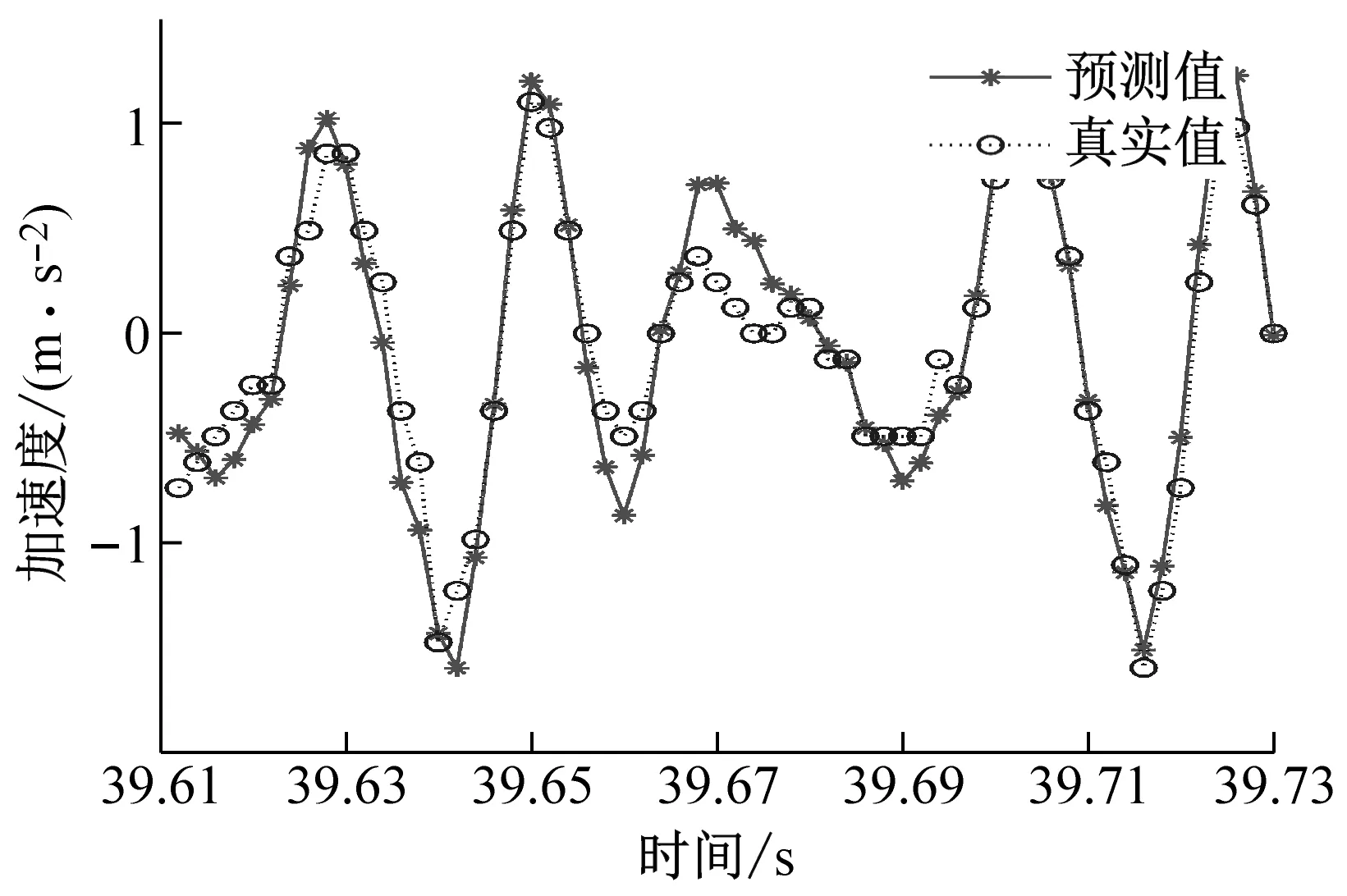
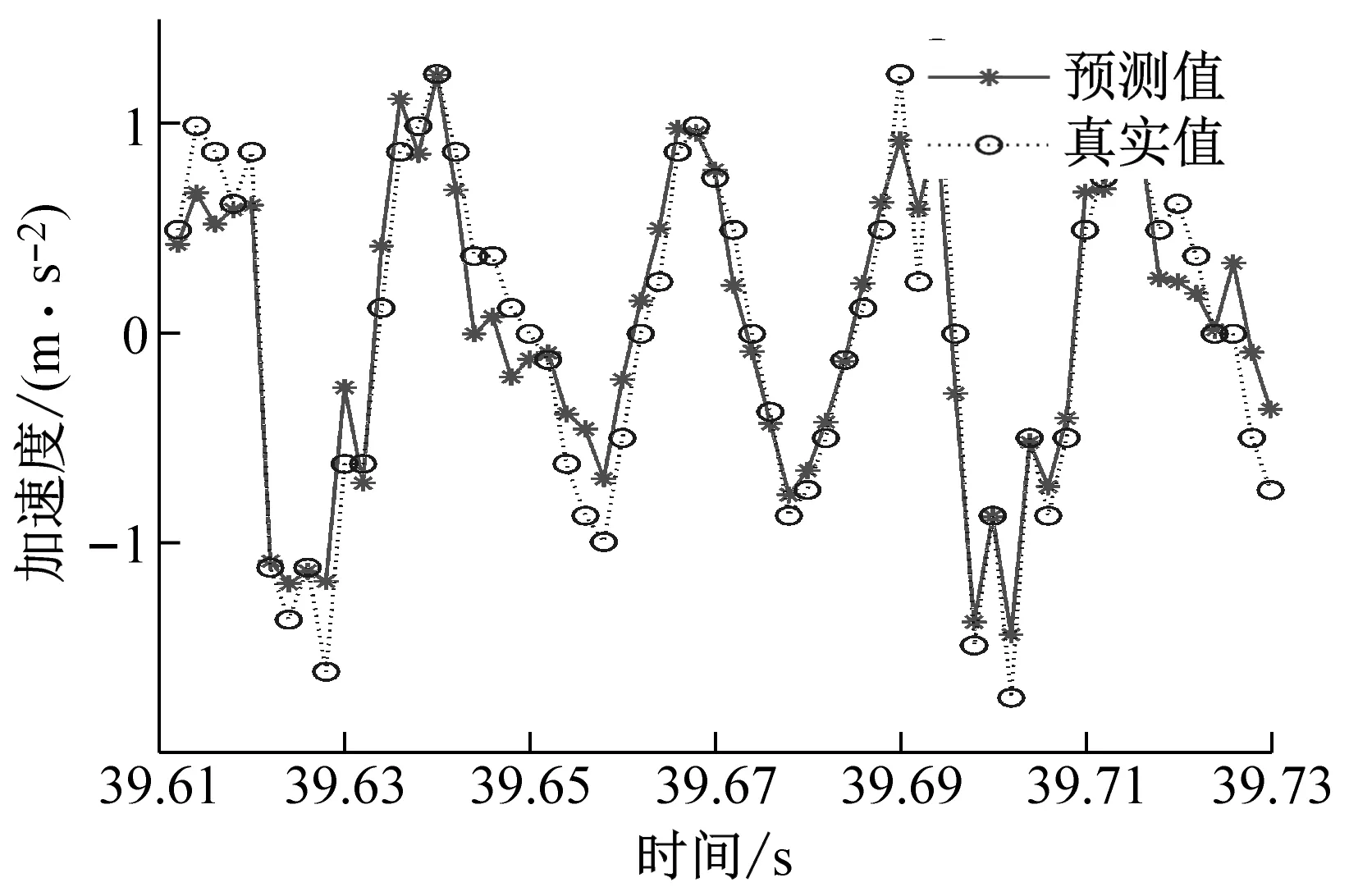
(a) ae=0.1 mm時工件X、Y兩個方向加速度信號預測圖

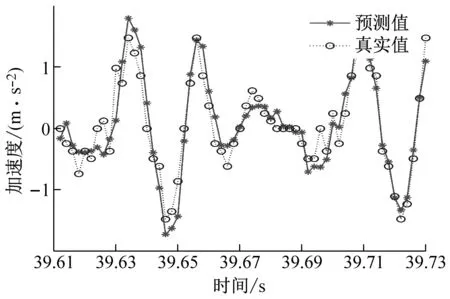
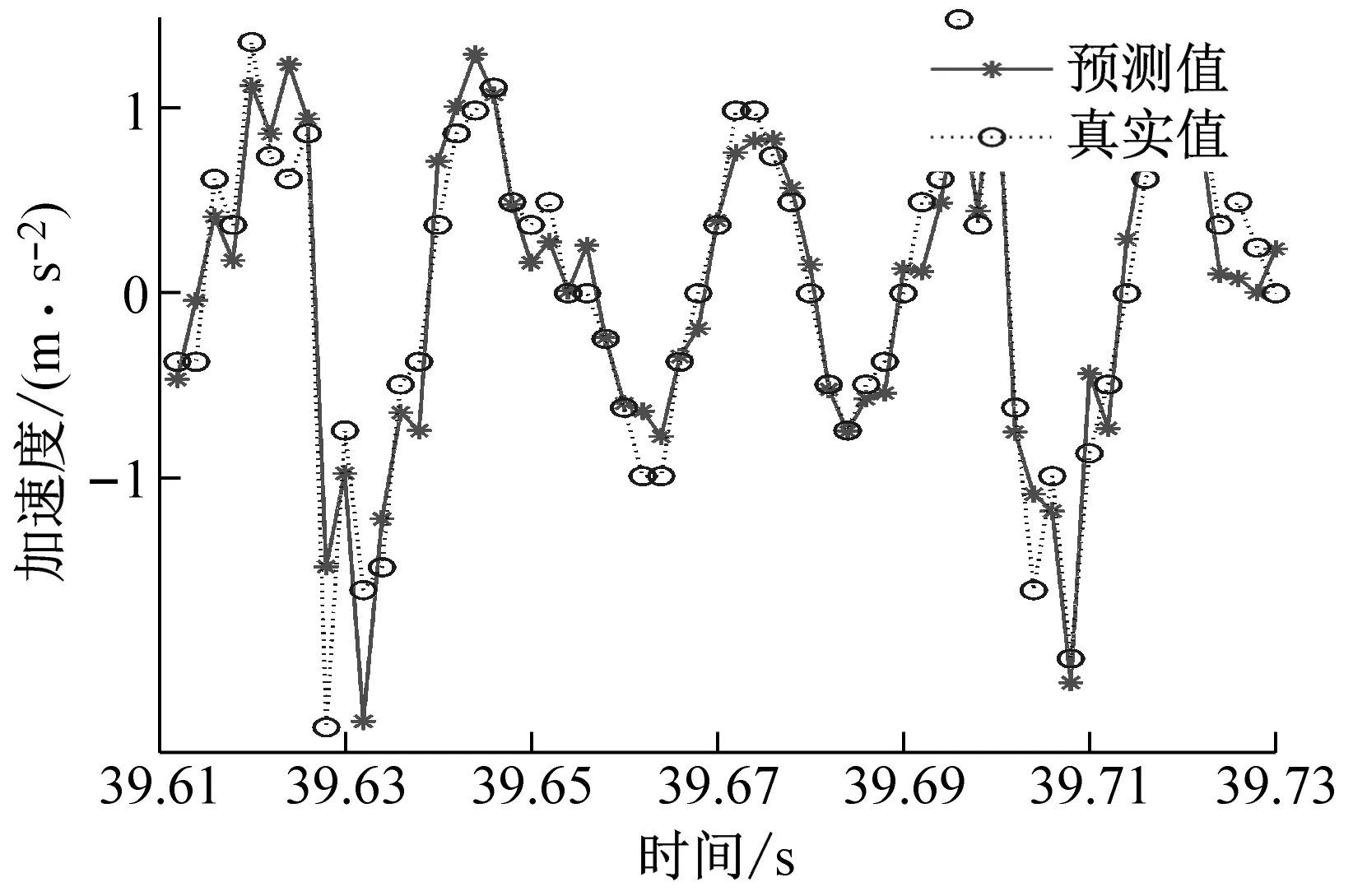
(b) ae=0.2 mm時工件X、Y兩個方向加速度信號預測圖

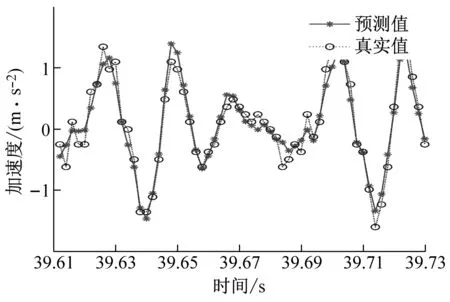
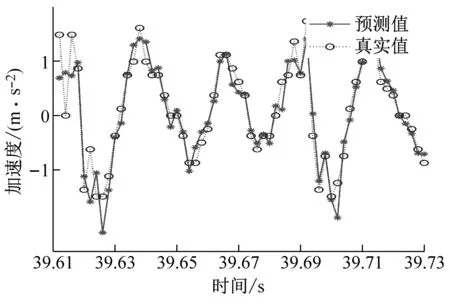
(c) ae=0.3 mm時工件X、Y兩個方向加速度信號預測圖

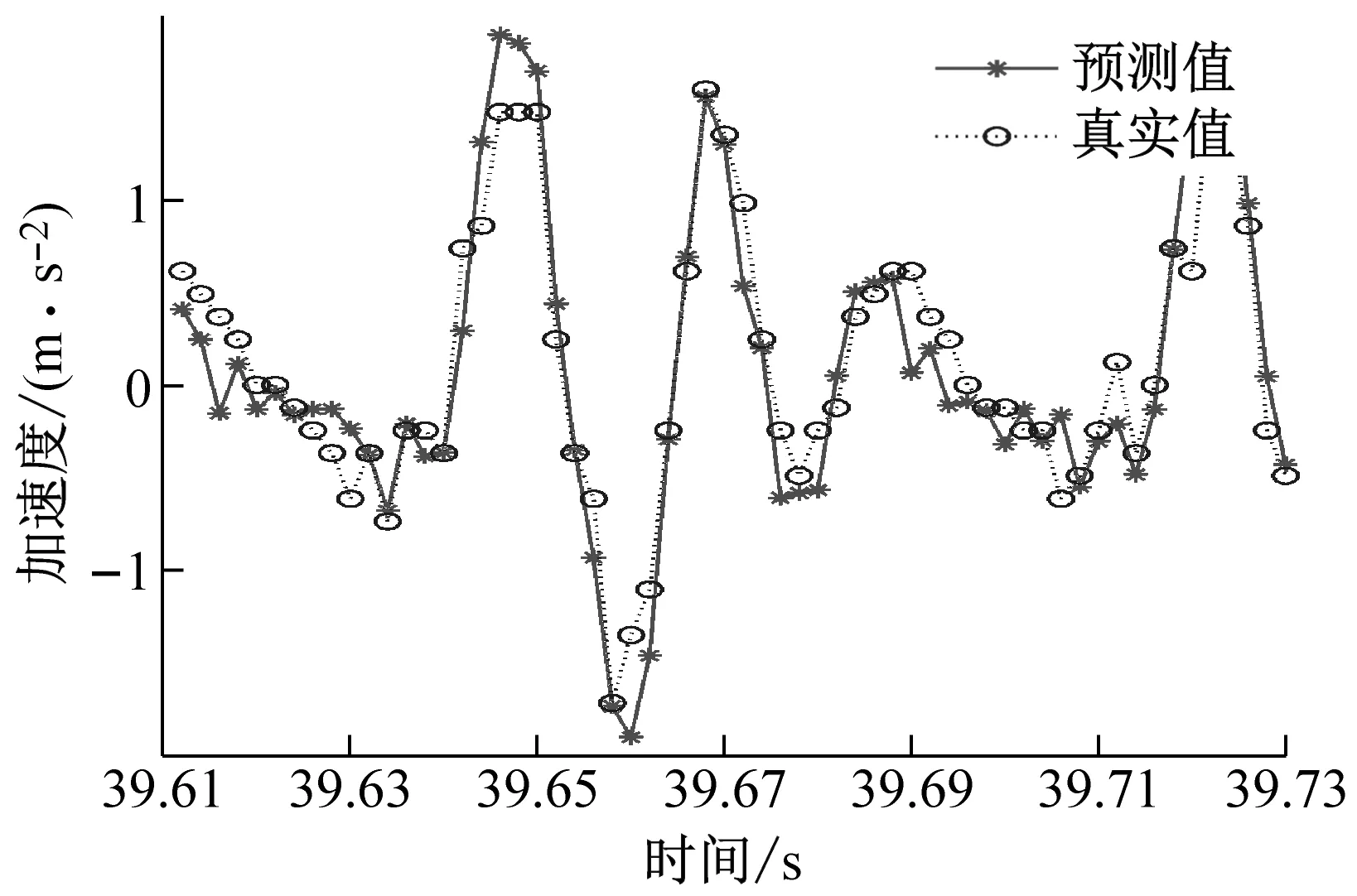
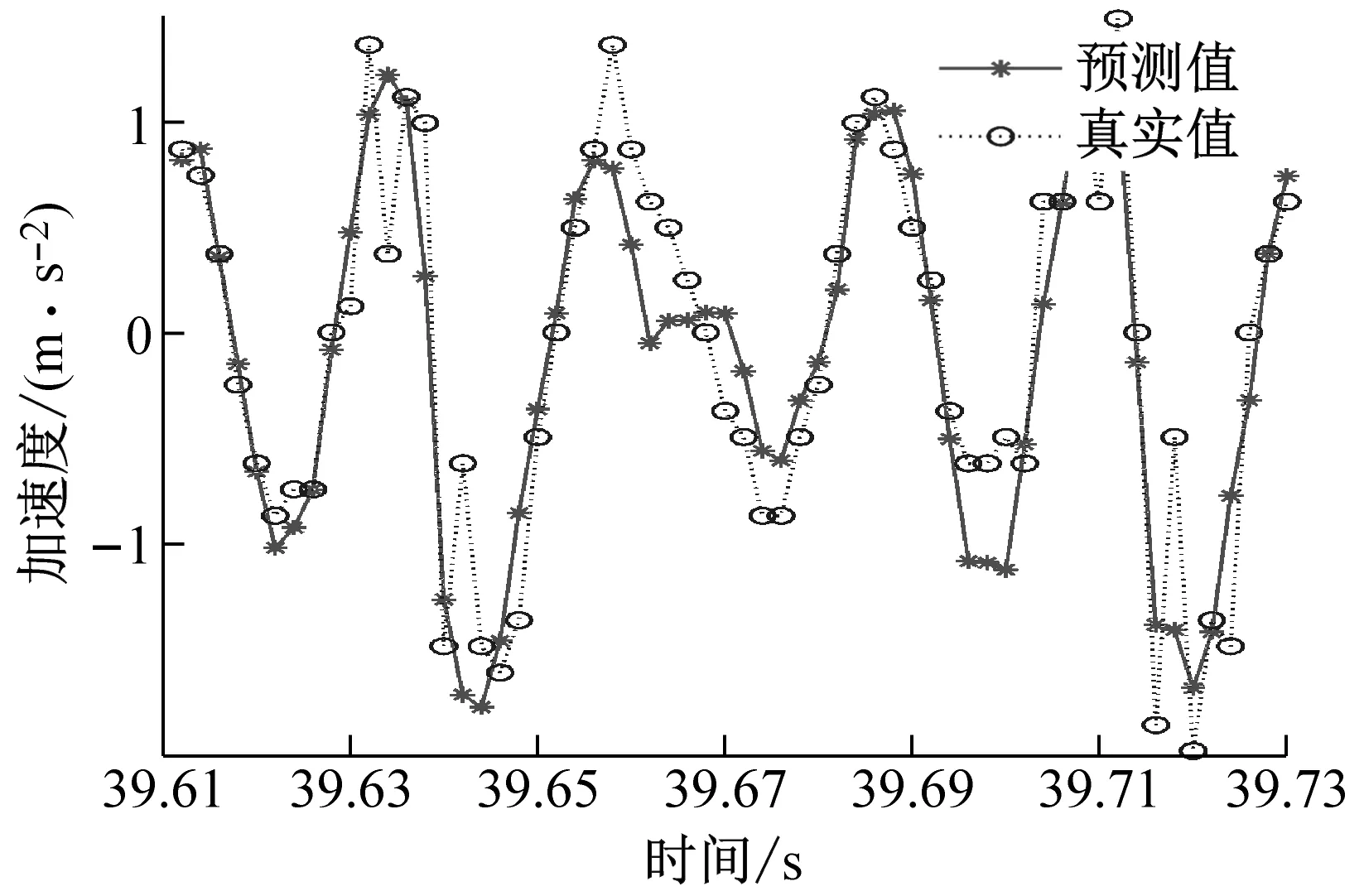
(d) ae=0.4 mm時工件X、Y兩個方向加速度信號預測圖圖9 不同變切深下的振動數據預測結果圖Fig.9 Vibration data prediction results at different variable depths of cut

從圖9中可以看出，不同切深下的加速度信號預測結果圖，可以明顯地看出GWO-SVR模型對工件X方向的預測曲線擬合度高于工件Y方向的預測曲線擬合度，所以工件X方向的預測精度是高于工件Y方向的。

銑削振動幅值的不同歸根到底是銑削力的差異，Y方向的銑削力要大于X方向的銑削力。在銑削過程中Y方向為主方向也就是進給方向，X方向為徑向方向，刀具在進給方向對于材料的切除率要大于刀具徑向方向對材料的切除率，在進給方向所受到的銑削力也就越大。

預測準確度的計算采取的方法是先計算預測值與實際值的差值，然后與實際值進行比較，具體預測準確度見表3。

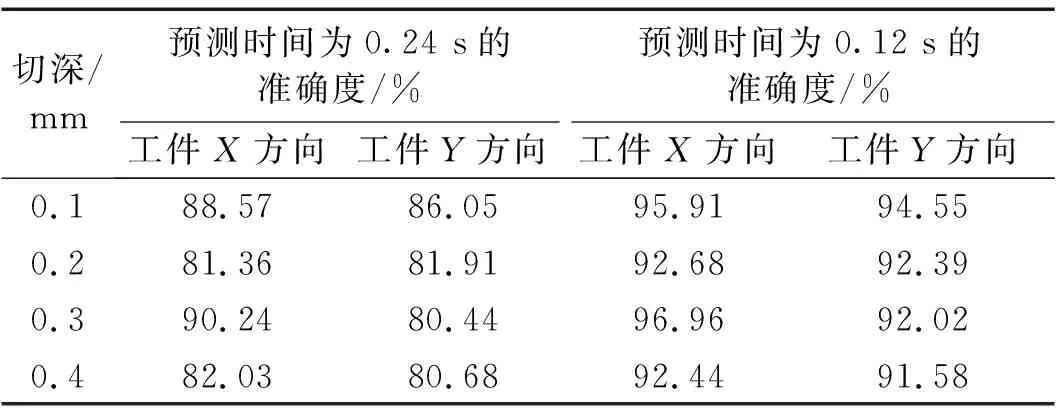
表3 工件X、Y方向銑削振動加速度信號預測準確度Tab.3 Prediction accuracy of vibration acceleration signal of workpiece in X and Y directions

如表3所示，在信號分解和前瞻預測方法確定的前提下，MSE的大小主要取決于原始振動信號數據的幅值大小，振動信號變化越強烈、非線性特征越強，得到的MSE結果也就是越差。因為多個子序列疊加的原因，不同的原始信號數據會產生較大的MSE差距，有時甚至為指數級別變化。當切深ae=0.30 mm時，加速度信號預測誤差最小，當預測時間為0.24 s時工件X方向準確度最高達到90.24%，當預測時間為0.12 s時工件X方向準確度最高達到96.96%，整體準確度(工件X方向和Y方向兩者共同的準確度)為94.49%。

分析中分別基于CEEMD-SVR模型、CEEMD-GA-SVR模型、CEEMD-PSO-SVR模型和CEEMD-GWO-SVR模型對數據進行預測，得到了四條預測曲線，如圖10所示。

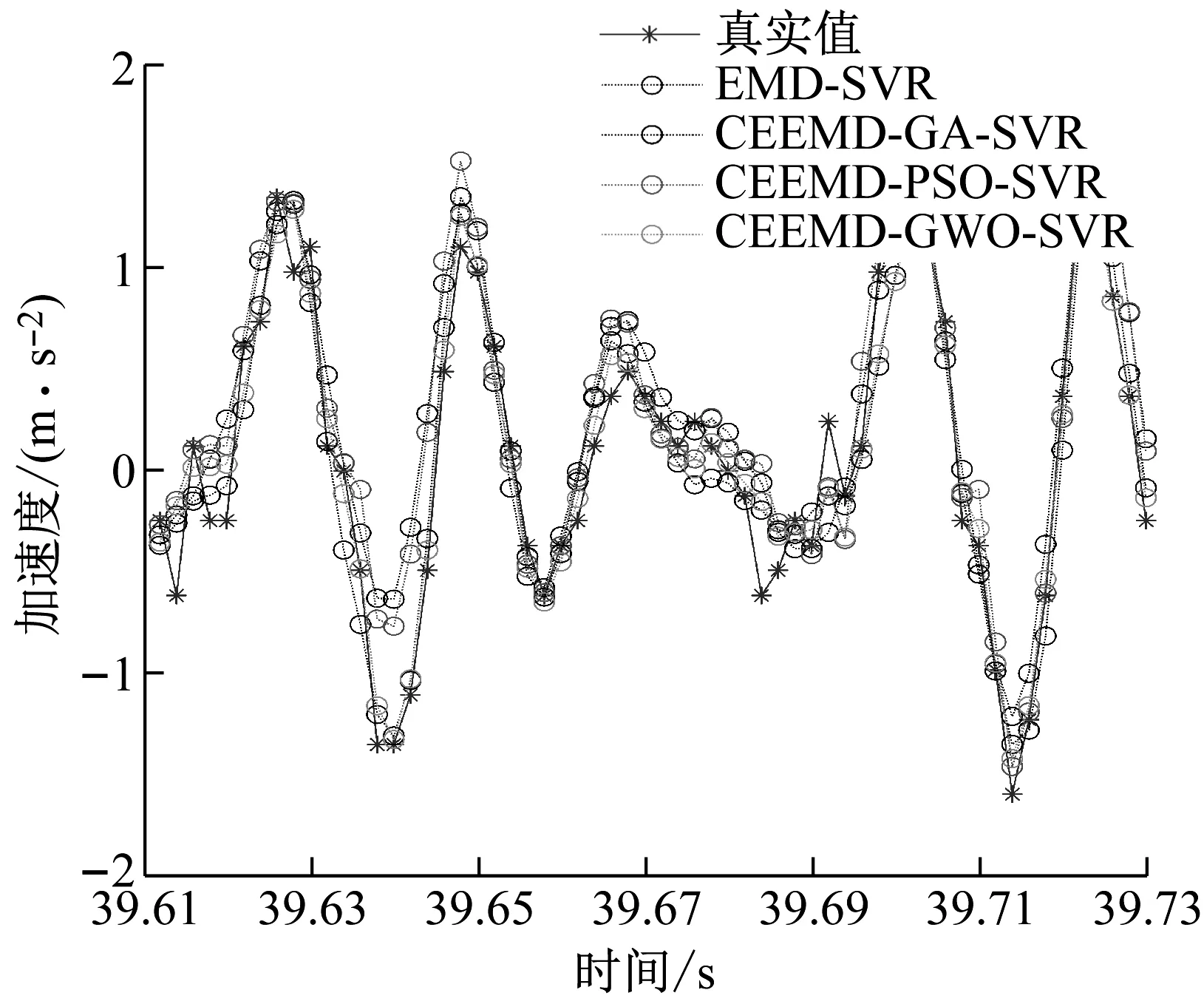
圖10 不同模型預測曲線圖Fig.10 Forecast curves of different models

從圖10可以看出基于CEEMD-GWO-SVR模型的預測數據精準度要高于EMD-SVR模型、CEEMD-GA-SVR模型和CEEMD-PSO-SVR模型的預測精準度，這是由于經過了CEEMD算法優化，信號分解效果要強于EMD分解算法；且CEEMD算法尋優效果也要優于GA和PSO算法。具體預測數據見表4。

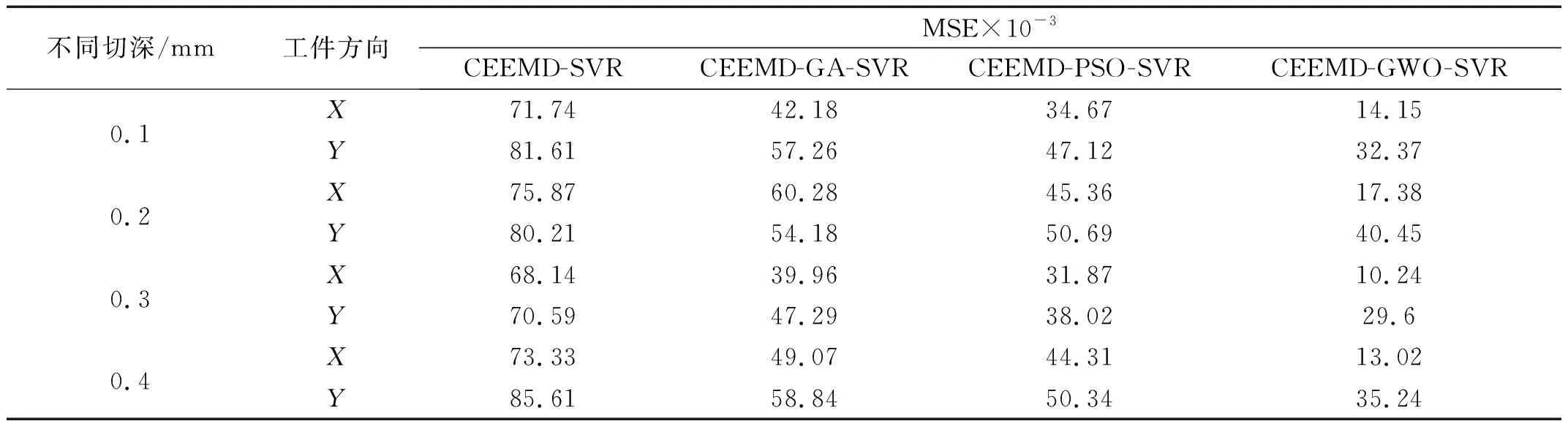
表4 預測時間為0.12 s的不同優化算法的性能對比Tab.4 Comparative of the performance of different optimization algorithms with a prediction time of 0.12 s

當切深ae=0.30 mm時，工件X方向加速度的預測相對誤差如圖11所示，此模型在預測剛開始時和預測中段有較大的誤差，前期誤差可能是剛開始時預測模型對預測集數據處于前期訓練階段，未完全掌握數據集規律，造成了預測精度低；而中期誤差是由于所選預測集數據中期局部極值較多，此類型真實值不好預測而造成的預測誤差增大；其余時間段預測精度都比較的高。

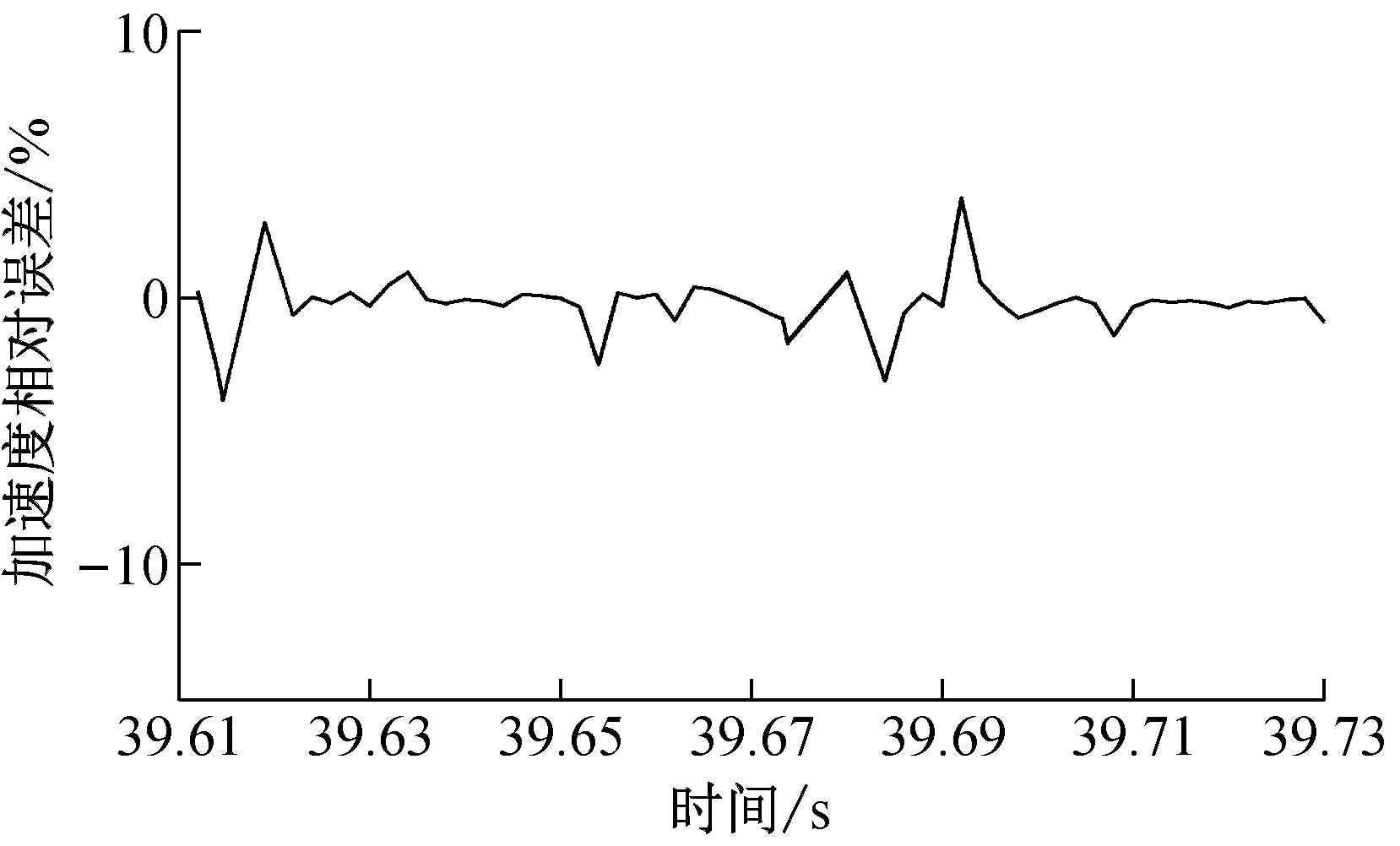
圖11 ae=0.3 mm時工件X方向加速度相對誤差圖Fig.11 Relative error graph of acceleration in X direction of workpiece when ae=0.3 mm

本文選取兩個訓練集和測試集比例，一個是訓練集為總體數據量的60%，測試集為總體數據量的40%，另一個是訓練集為總體數據量的20%，測試集為總體數據量的80%。當訓練集時序數據減少，預測時序數據增加1倍時，觀察所預測數據的精準度變化情況如圖12和圖13所示。

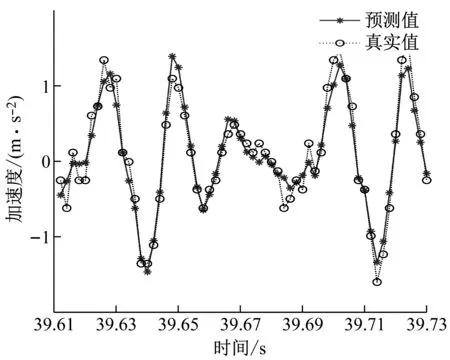
圖12 預測時間0.12 s時的預測曲線圖Fig.12 Forecast curve diagram at forecast time 0.12 s

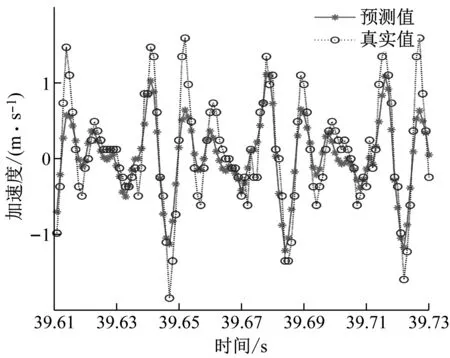
圖13 預測時間為0.24 s時的預測曲線圖Fig.13 Forecast curve diagram at forecast time 0.24 s

當訓練集的數據比例由60%下調到了20%，預測誤差明顯上升，預測精準度下降，這是由于訓練集比例的降低會造成SVR所訓練的樣本個數的下降，訓練樣本數不足導致了SVR模型無法充分地學習數據樣本的規律，從而導致預測精度的下降，為了進一步定量地評估預測結果，分別計算預測時間分別為為0.12 s和0.24 s的MSE(均方誤差)，計算結果如表4、表5所示。其中MSE函數一般用來檢測模型的真實值和預測值之間的偏差，MSE值越大，表明預測結果越差。MSE公式為

(19)

表5 預測時間為0.24 s的不同優化算法的性能對比Tab.5 Comparative of the performance of different optimization algorithms with a prediction time of 0.24 s

從表4和表5的試驗結果可以看出，預測時間為0.12 s的預測步長模型的MSE要優于預測時間為0.24 s的預測步長模型的MSE,比如切深ae=0.30 mm時，基于CEEMD-GWO-SVR模型的工件X方向0.12 s預測步長的MSE為10.24要小于0.24 s預測步長MSE的15.31，所以0.12 s預測步長模型的預測性能要優于0.24 s預測步長模型的預測性能。

其中切深ae=0.30 mm時同一預測模型的MSE要低于其他切深預測模型的MSE，而且工件X方向MSE低于工件Y方向的MSE，如表4，當切深為ae=0.30 mm時工件X方向的MSE為10.24，當切深為ae=0.10 mm時工件X方向的MSE為14.15，當切深為ae=0.20 mm時工件X方向的MSE為17.38，切深為ae=0.40 mm時工件X方向的MSE為13.02；當切深ae=0.30 mm時工件X方向的MSE為10.24，切深為ae=0.30 mm時工件Y方向MSE為29.60。

在對工件X方向加速度信號進行步長為0.12 s的預測且切深ae=0.30 mm時，CEEMD-SVR模型、CEEMD-GA-SVR模型、CEEMD-PSO-SVR模型和CEEMD-GWO-SVR模型各自的MSE分別為68.14、39.96、31.87和10.24，CEEMD-GWO-SVR模型預測得到的MSE誤差要低于CEEMD-SVR模型、CEEMD-GA-SVR模型、CEEMD-PSO-SVR模型，所以相比于CEEMD-SVR模型、CEEMD-GA-SVR模型、CEEMD-PSO-SVR模型，CEEMD-GWO-SVR模型具有更小的預測誤差，證明了此方法更適用于預測銑削加速度信號。

5 結 論

(1) 提出了針對拼接模具銑削振動信號的CEEMD分解的方法，采取分解6層IMFs和殘余項的方法，得到了穩定的子序列供后續的前瞻預測；

(2) 采用灰狼優化算法對支持向量機回歸(SVR)中的參數C和g進行尋優，得到銑削振動信號規定時間段內的全局最優參數，然后將CEEMD和GWO-SVR結合起來預測銑削拼接模具振動加速度信號。試驗數據顯示，在對工件X方向加速度信號進行步長為0.12 s的預測且切深ae=0.30 mm時，CEEMD-SVR模型、CEEMD-GA-SVR模型、CEEMD-PSO-SVR模型和CEEMD-GWO-SVR模型各自的MSE為68.14、39.96、31.87和10.24，CEEMD-GWO-SVR模型的MSE低于其他三種模型的MSE，該方法相比其他方法具有較高的預測精度和更好的泛化能力，在預測步長為0.12 s時總體預測準確率為94.49%。

(3) 在淬硬鋼拼接區銑削過程中，當切深為0.10 mm、0.20 mm、0.30 mm和0.40 mm時各自的MSE為14.15、17.38、10.24、13.02；在切深ae=0.30 mm時，拼接區銑削振動信號預測誤差最小；在振動加速度信號為0.3 s的時間段內，0.12 s預測步長MSE為17.38，0.24 s預測步長MSE為23.89。在0.3 s的數據集中，0.12 s預測步長模型(預測集為全部數據集的40%)的預測誤差小于0.24 s預測步長模型(預測集為全部數據集的80%)。