基于有限測量信息的兩步響應重構方法

史鵬程， 彭珍瑞， 董康立

(1. 蘭州交通大學 機電工程學院， 蘭州 730070； 2. 浙江大學 生物醫學工程與儀器科學學院， 杭州 310027)

隨著我國經濟的飛速發展，近年來國內大跨度橋梁以及高層建筑的數量日益增加，結構各處的響應數據是對其進行實時健康監測的重要基礎。然而這些結構的服役時間往往長達幾十年甚至上百年，遠遠超過測量其動態響應的傳感器的壽命。因此基于有限的測量信息，對結構其余各處響應進行重構的結構響應重構技術具有重要的意義[1-4]。

現有的響應重構技術大致可分為兩類：第一類基于模態分析或傳遞率的思想，建立已知測量響應和需要重構響應之間的傳遞關系，從而獲得所需的各點的動態響應。Kammer[5]提出基于模態分析的響應重構方法，利用可測量的響應數據和結構模態振型矩陣來重構不可測位置處的動態響應。Zhang等[6-7]采用這種方法，針對梁模型研究了雙重傳感器下的結構應變、位移響應重構。Ribeiro等[8]最早提出傳遞率的概念，并將之應用于單自由度系統及多自由度系統的位移響應重構。Law等[9]將位移傳遞率擴展到了加速度傳遞率，并將這種方法應用到子結構的響應重構中，在響應計算中結合一階保持輸入逼近，提高了動態響應的準確性。Li等[10]又將基于傳遞率的響應重構方法從頻域擴展到了小波域中，采用離散小波變換對結構和子結構系統分別進行響應重構計算，精度要高于離散傅里葉變換響應重構的精度。此類方法需基于精準的有限元模型，且沒有考慮傳感器測量噪聲對重構精度的影響。

第二類基于卡爾曼濾波(Kalman filter, KF)算法的結構響應重構方法。張笑華等[11]基于KF算法對二維桁架的應變和位移響應進行了重構，同時對位移和應變兩種傳感器的數量和位置進行了優化。Xu等[12]使用KF對大跨度懸索橋進行應變、位移、加速度的響應重構，并結合逐步消去法對多類型傳感器進行優化布置。任鵬等[13]分別使用增廣卡爾曼濾波法和傳遞率法在未知外部激勵的情況下對一鋼桁架進行了應變響應重構，并對比了兩種方法的優劣。董康立等[14]基于激勵計算卡爾曼濾波算法驗證了對外部激勵和各處響應進行重構的有效性，并以響應重構精度為目標，使用螢火蟲算法和逐步消去法分別進行傳感器優化布置。此類方法是一種不確定性方法，可以有效地降低模型誤差和測量噪聲對于響應重構帶來的影響。但使用KF算法必須事先假設測量噪聲為高斯白噪聲，而實際工程中的噪聲卻多為有色噪聲，若把有色噪聲當作白噪聲處理，必然影響響應重構精度。粒子濾波算法可以很好地處理有色噪聲的影響，但使用傳統粒子濾波算法進行響應重構，會出現粒子貧化現象，從而影響響應重構精度。近年來不少學者將群體智能優化算法引入粒子濾波中[15-16]，替代原有的重采樣過程，皆取得了較好的效果。

目前，對各類響應重構方法的研究通常也伴隨著以提高響應重構精度為目的的傳感器優化布置方案的研究[17-20]，但是在結構的服役過程中傳感器的損壞往往是隨機的，不可能符合優化布置中的方案。

因此，針對以上問題，首先基于已知測點的應變響應和位移響應，通過建立已知測量響應和所需重構響應的關系，重構出所需重構點的應變和位移響應。針對有色噪聲問題，引入粒子濾波算法，同時結合螢火蟲算法替代傳統重采樣過程，改善粒子貧化問題。然后結合改進的粒子濾波算法，減小模型誤差和測量噪聲對于重構結果的影響，得到最終的響應重構結果，實現利用正常測量的響應對因傳感器損壞而丟失或其余未布置傳感器處的響應的重構。最后以一個二維桁架結構為例，驗證所提方法的有效性。

1 結構響應重構

在線性結構中，結構的應變響應和位移響應可以表示為

(1)

式中：ε為結構應變響應；d為結構位移響應；Ψs為所選擇的前s階應變振型；Φs為所選擇的前s階位移振型；Γs為Ψs和Φs組成的矩陣；q為模態坐標向量。

測量位置的動態位移響應和應變響應同樣也可表示為

(2)

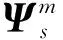
應變振型矩陣和位移振型矩陣的關系可表示為

Ψ=TΦ

(3)

式中：T為應變位移轉換矩陣，與有限元模型的形函數有關。

結合式(1)和式(2)，可重構出所需位置的動態響應

(4)

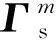
(5)

(6)

式中：σε和σd分別為應變和位移的測量噪聲標準差。重構式(4)可重新寫為

(7)

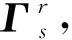
2 基于狀態空間的濾波處理

結構的二階運動方程可以用模態坐標表示為

(8)

式中：q為模態坐標；ξ為阻尼矩陣；ω0為模態頻率矩陣；u為外部激勵向量；L為激勵映射矩陣；Φ為模態位移振型矩陣。

將式(8)轉化為狀態空間方程并離散化

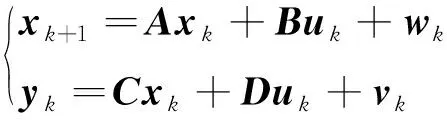
(9)

式中：xk，yk和uk分別為離散后的狀態向量，觀測向量和外部激勵向量；A和B分別為離散化后的狀態矩陣和輸入矩陣；C和D分別為輸出矩陣和直接傳輸矩陣；wk和vk分別為由于模型的不確定性造成的系統噪聲和測量誤差造成的測量噪聲。式(9)中的各項具體表示為

(10)

(11)

(12)

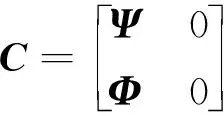
(13)

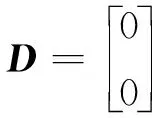
(14)

通過建立以上狀態空間模型，可以將式(7)得到的響應作為狀態空間中的觀測值，并通過濾波處理得到結構真實響應：

(15)

式中：Ce和De分別為結構對應位置輸出矩陣和直接傳輸矩陣，是矩陣C和D的子矩陣。

3 粒子濾波算法

粒子濾波是一種基于狀態空間模型，結合貝葉斯估計和抽樣理論的濾波算法。其基本思想是利用一組樣本對條件后驗密度函數進行近似，用樣本均值取代原有的積分運算，獲得對系統的最小方差估計。系統狀態空間模型可表示為

xk=f(xk-1,wk-1)

(16)

yk=h(xk,vk)

(17)

式中：xk為狀態向量；wk-1為系統噪聲；yk為觀測向量；vk為測量噪聲。

設狀態初始概率密度p(x0|y0)=p(x0)，則預測方程為

(18)

狀態更新方程為

(19)

其中

(20)

采樣的重要性函數q(x0:k|y1:k)可以改寫為

(21)

則權值公式為

(22)

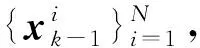
(23)

式中：δ(·)為狄拉克函數。

概率密度更新公式為

(24)

將權值歸一化后計算狀態向量

(25)

(26)

以上為粒子濾波算法基本流程，在粒子集的不斷迭代更新過程中，會使大多數粒子的權值接近0，少數粒子占有較大的權重，即粒子退化現象。使整個過程中的大量計算耗費在無意義的極小權值粒子上，針對這一問題，Gordon等[21]提出重采樣來解決粒子退化問題，即復制大權值粒子，刪除小權值粒子。但是傳統重采樣方法由于刪除了小權值粒子，同時復制大權值粒子，反復重采樣導致后代粒子多為采樣前某幾個大權值粒子的后代，從而減小了粒子的多樣性，產生粒子貧化問題，導致算法整體性能的下降。

4 螢火蟲算法

螢火蟲算法是模仿螢火蟲運動行為的一種智能算法。螢火蟲個體之間的移動主要依賴于熒光亮度和吸引度兩個參數，熒光亮度反映螢火蟲所處位置的優劣并決定移動方向，吸引度與螢光亮度成正比，決定螢火蟲的移動距離。螢火蟲個體之間通過向周圍螢光亮度更高的螢火蟲移動實現尋優。

螢光亮度可以表示為

I=I0e-γr

(27)

式中：I0為初始螢光亮度；γ為熒光吸收系數；r為螢火蟲個體之間的距離。

螢火蟲之間的吸引度可以表示為

β=β0e-γr2

(28)

式中：β0為初始吸引度。

螢火蟲個體之間的運動更新可以表示為

(29)

式中：xi和xj分別為兩個螢火蟲i和j的位置；α為步長因子。

5 結合螢火蟲算法的粒子濾波

5.1 改進螢火蟲算法

針對傳統重采樣方法帶來的粒子貧化問題，將螢火蟲算法引入粒子濾波中，替代傳統的重采樣方法，改善粒子貧化問題。由于螢火蟲算法在尋優過程中單個螢火蟲個體需要與其他所有的螢火蟲個體之間計算相互之間的吸引度、螢光亮度等參數，并與其產生相對移動。若將其直接引入粒子濾波，將增加計算復雜度，影響濾波的實時性。同時，由于式(29)中添加隨機擾動項避免算法陷入局部最優，但由式(10)可知狀態向量中的參數并不在一個數量級，直接加入同一數量級的擾動項必然不可行。

針對以上問題，結合粒子濾波以及響應重構的需要，對于傳統螢火蟲算法作如下改進后再將其引入粒子濾波算法。

修正運動更新公式

(30)

式中：xbest為k時刻的全局最優值。改進后的運動更新方案使得螢火蟲個體i在k時刻只需與全局最優值之間進行參數計算并進行相對移動，這大大降低了運算復雜度，提高了濾波實時性。

修正螢光亮度公式

(31)

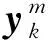
5.2 算法步驟

(32)

步驟2將螢火蟲算法中的螢火蟲個體看作粒子濾波中的粒子，引入改進后的螢火蟲算法指導粒子移動：根據式(28)計算粒子i與全局最優值xbest之間的吸引度,并依據式(30)指導粒子向全局最優值移動。

步驟3當所有粒子完成位置更新后，根據式(31)計算每個粒子的熒光度值，并更新最優粒子。

步驟4當熒光亮度小于閾值時，證明預測值與觀測值差值已較小，粒子分布已接近真實分布，停止迭代，若未達到閾值則轉入“步驟2”。或當迭代次數達到設置的最大迭代次數時，亦停止迭代過程。

步驟5依據式(24)～式(26)計算粒子權重并歸一化后計算最終狀態輸出。

為避免在使用螢火蟲算法指導粒子進行移動時迭代次數過多而使得粒子過于收斂，導致粒子多樣性降低，但同時又要保證粒子對高似然區域有著較好的覆蓋能力，能反應出系統真實的狀態。為此，在“步驟4”中設置算法的最大迭代次數和熒光度閾值控制其迭代次數。

6 數值算例

采用二維桁架模擬整個響應重構過程，以驗證所提方法的有效性。如圖1所示。該桁架結構共有14個節點，25個單元和25個自由度。彈性模量、密度和泊松比分別為210 GPa、7 850 kg/m3和0.3。選取前六階模態振型為目標模態進行響應重構，模態頻率分別為17.72 Hz、58.89 Hz、85.48 Hz、113.67 Hz、169.98 Hz、220.22 Hz。在第4節點的Y方向施加隨機白噪聲激勵，激勵的時程曲線如圖2所示。提取10、11、12單元的應變響應和4、5、7節點的Y方向的位移響應，并加入3%的有色噪聲作為正常工作的傳感器的測量響應，并將結構其余單元、節點未加噪聲的響應yr作為其余所需重構位置以及傳感器失效位置的響應。有色噪聲的功率譜如圖3所示。由圖3可知，有色噪聲的功率譜分布是不均勻的。

圖1 二維桁架結構Fig.1 Two-dimensional truss structure

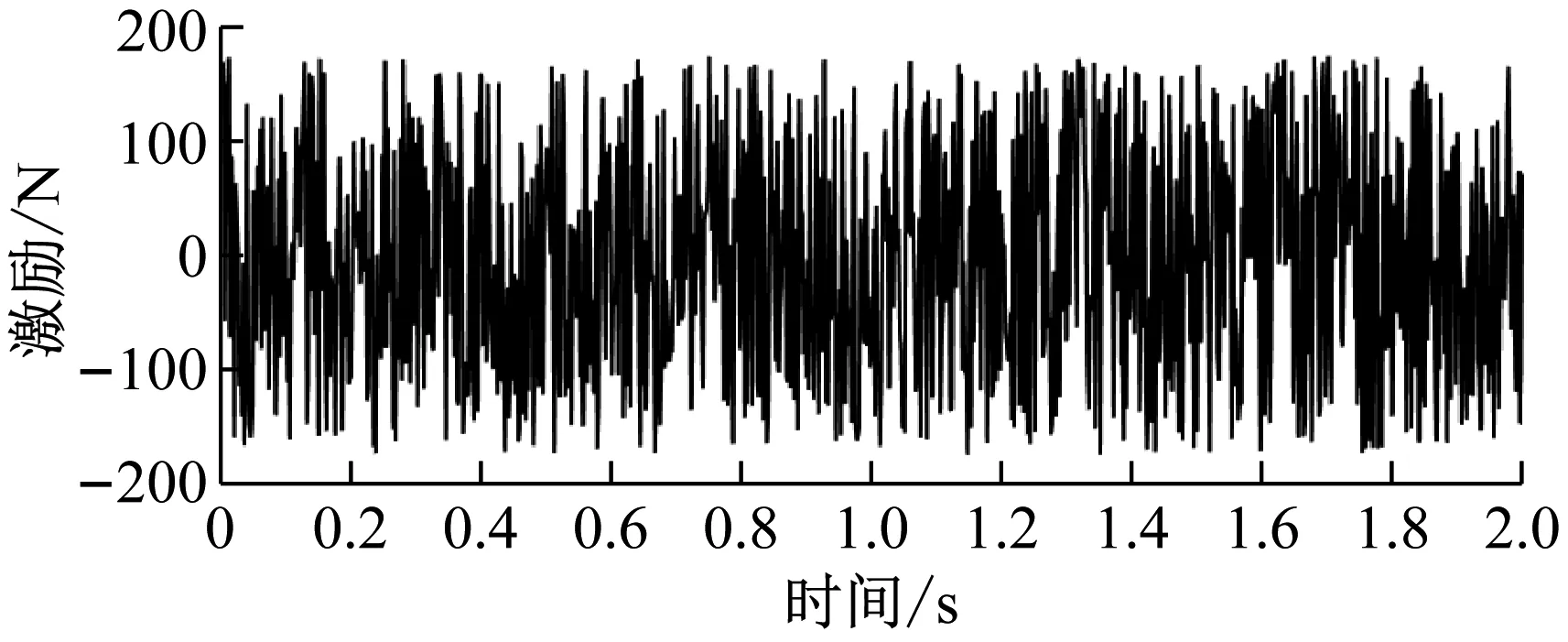
圖2 隨機白噪聲激勵Fig.2 Excitation of random white noise

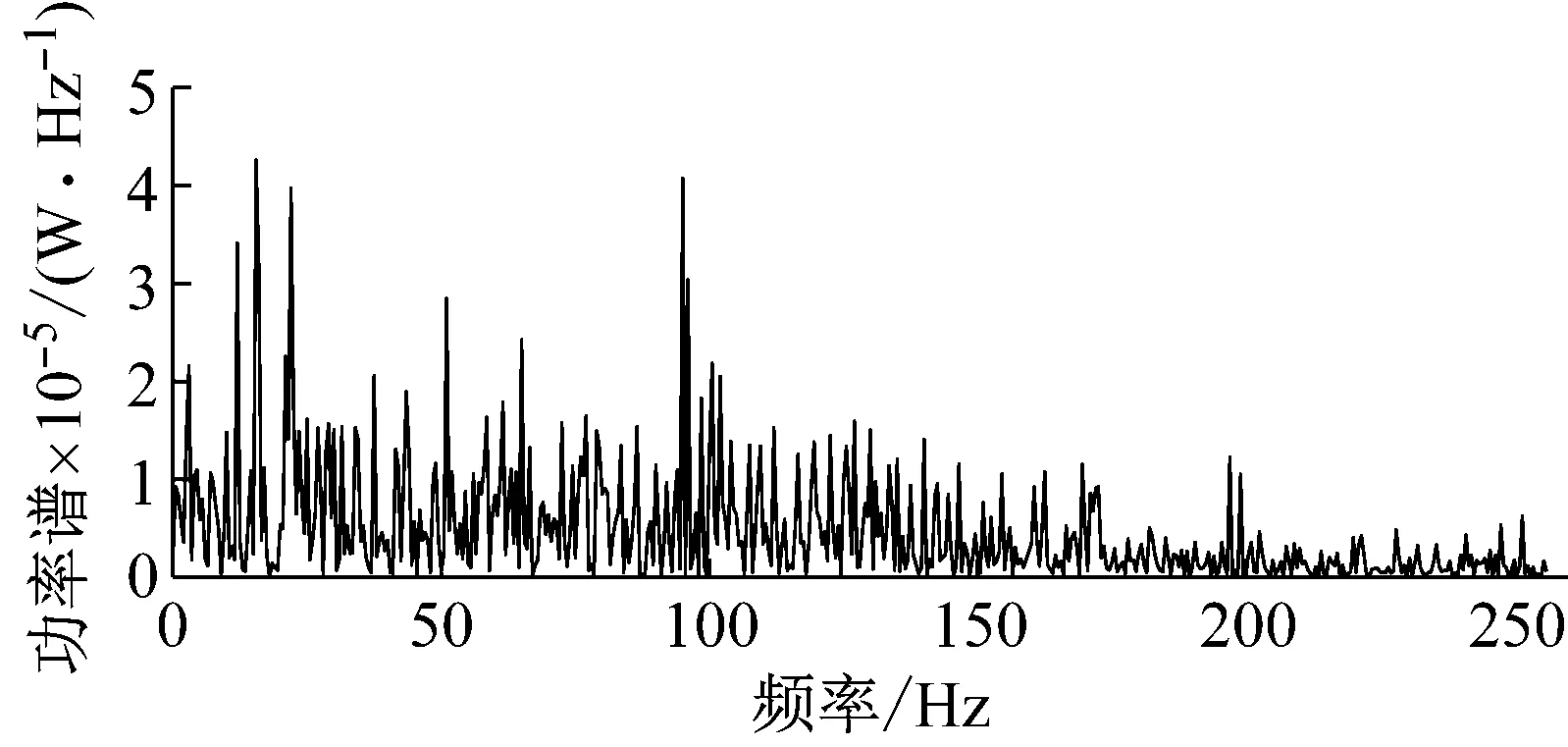
圖3 有色噪聲功率譜Fig.3 Power spectrum of colored noise

將提出的兩步響應重構方法與文獻[11]中的響應重構方法進行對比，由于文獻[11]中的KF算法不適合處理有色噪聲問題，因此將改進粒子濾波算法替換原有的KF算法直接進行響應重構。在改進的粒子濾波算法中，設置最大迭代次數為15次，熒光度向量求模后設置閾值為10。

在結合螢火蟲算法的粒子濾波中，由于粒子維數較大，不容易直觀地看出是否發生粒子貧化或粒子退化現象，因此通過粒子權重，間接反映粒子質量。某一時刻的粒子權重，如圖4所示。從圖4可知，粒子權重分布均勻，不存在粒子退化或粒子貧化問題。

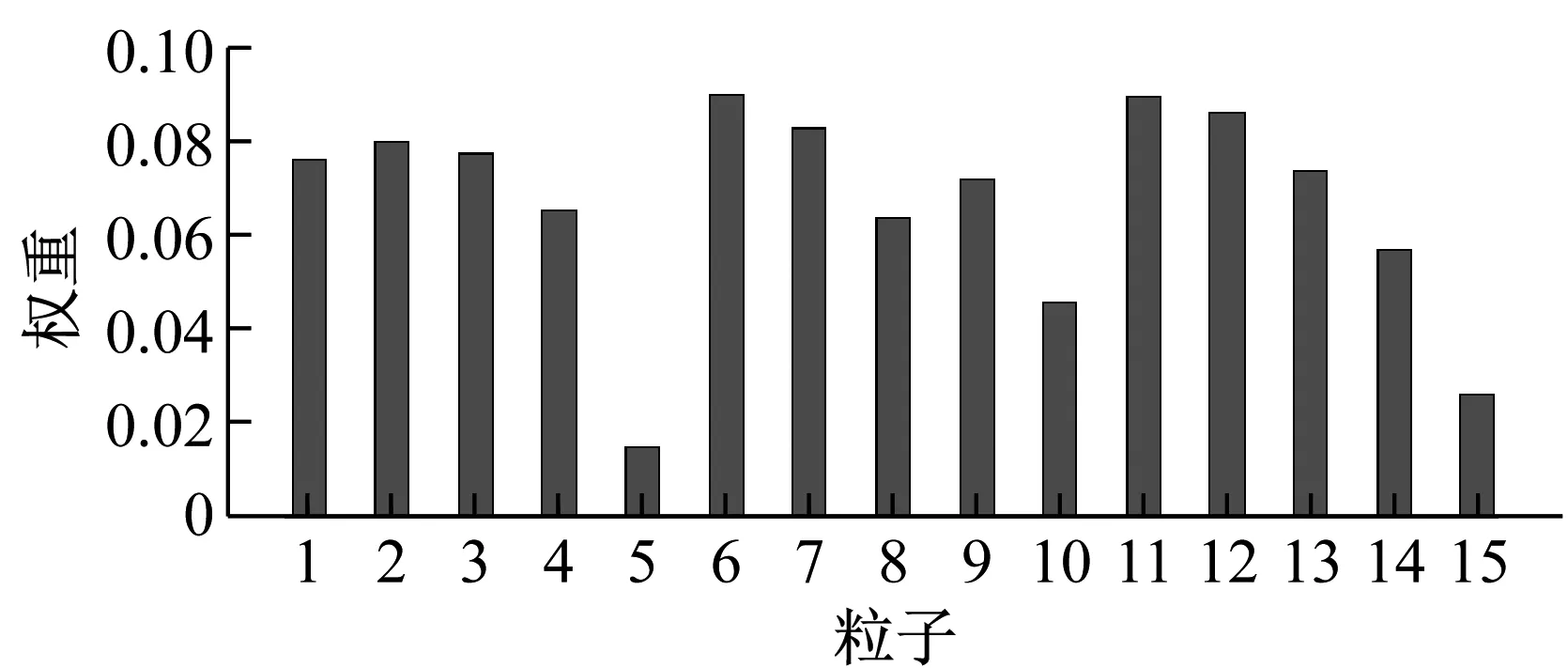
圖4 粒子權重Fig.4 Weight of particles

方法1本文提出的分兩步進行響應重構方法，首先對各類所需重構響應進行直接計算，第二步再使用粒子濾波進行濾波處理。

方法2基于粒子濾波算法通過測量響應直接進行響應重構。

設定9單元、19單元的應變傳感器以及9節點、11節點Y方向的位移傳感器失效，通過現有的10單元、11單元、12單元的應變傳感器和4節點、5節點、7節點的Y方向的位移傳感器測得的響應，對傳感器失效處的響應以及其他所有各點的響應進行重構。

兩種方法分別對傳感器失效處的應變和位移響應重構的結果，如圖5和圖6所示。從圖可知，兩種方法重構的響應曲線均能較好地擬合測量響應曲線，均能對于缺失響應進行重構。

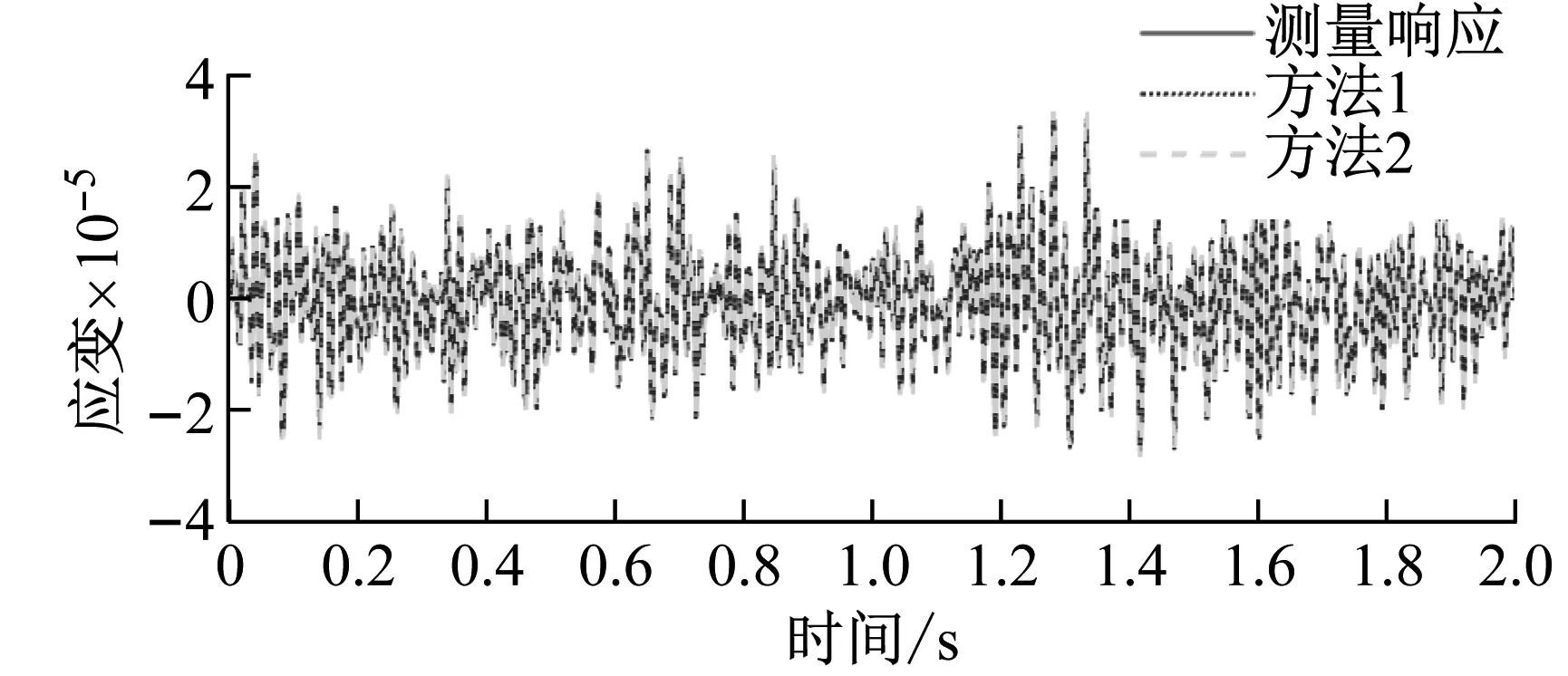
(a) 9單元應變

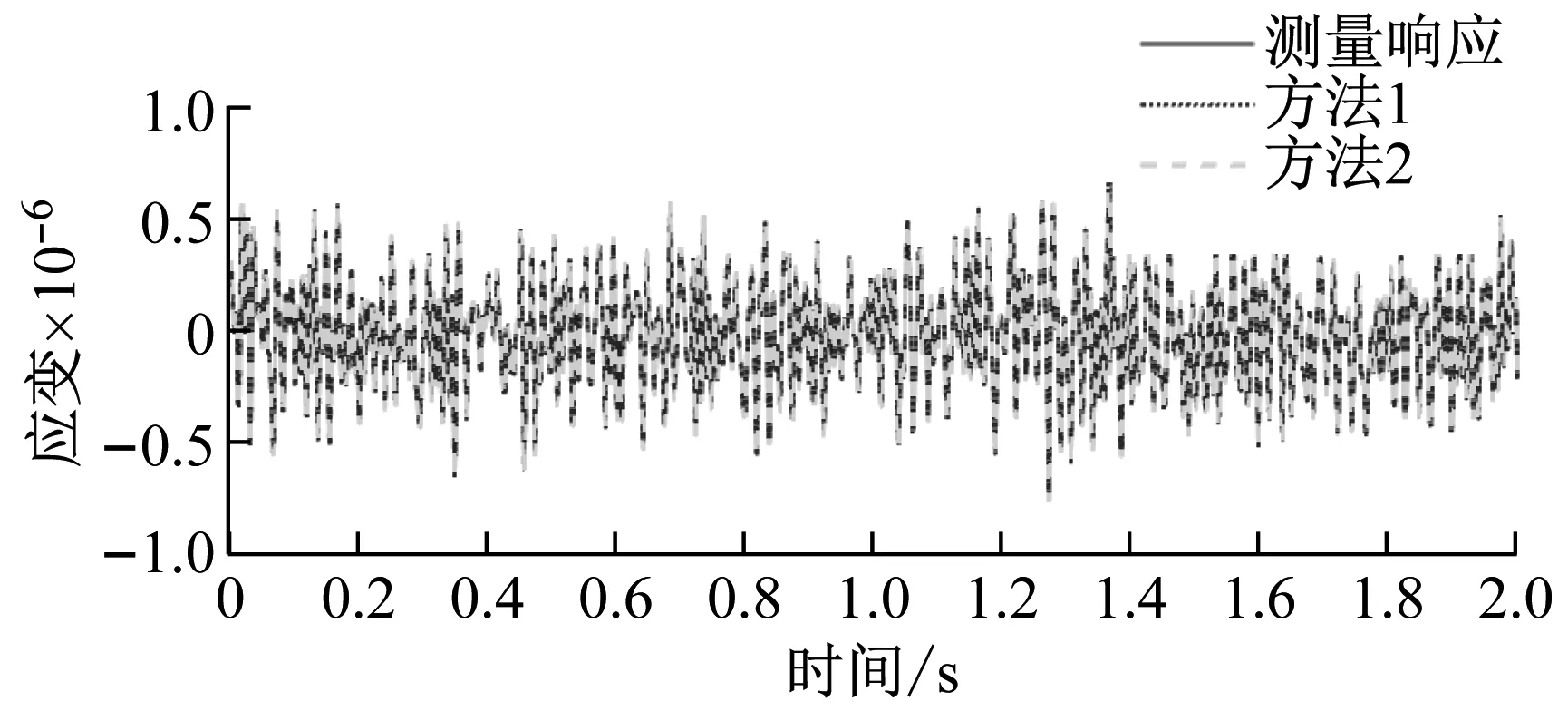
(b) 19單元應變圖5 重構應變響應與測量響應對比Fig.5 Comparison of reconstructed and measured strain responses

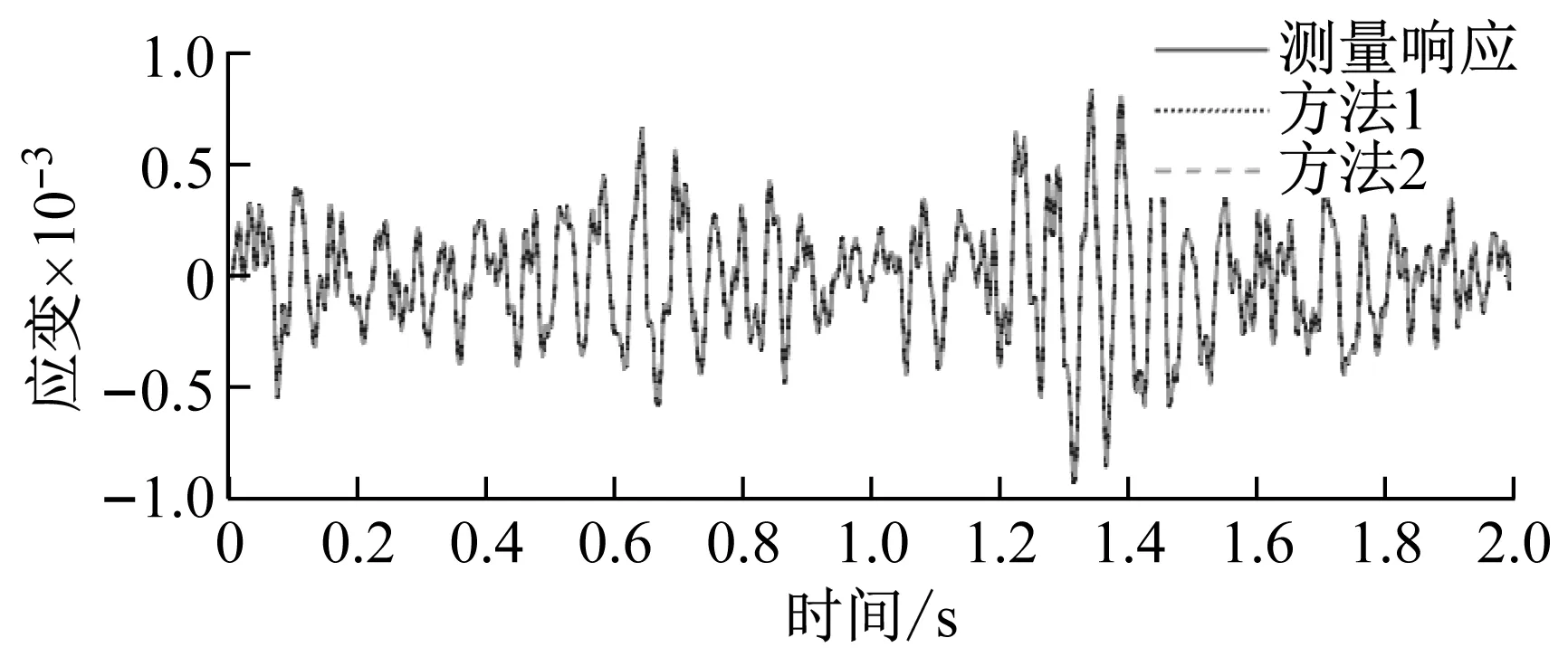
(a) 9節點Y向位移

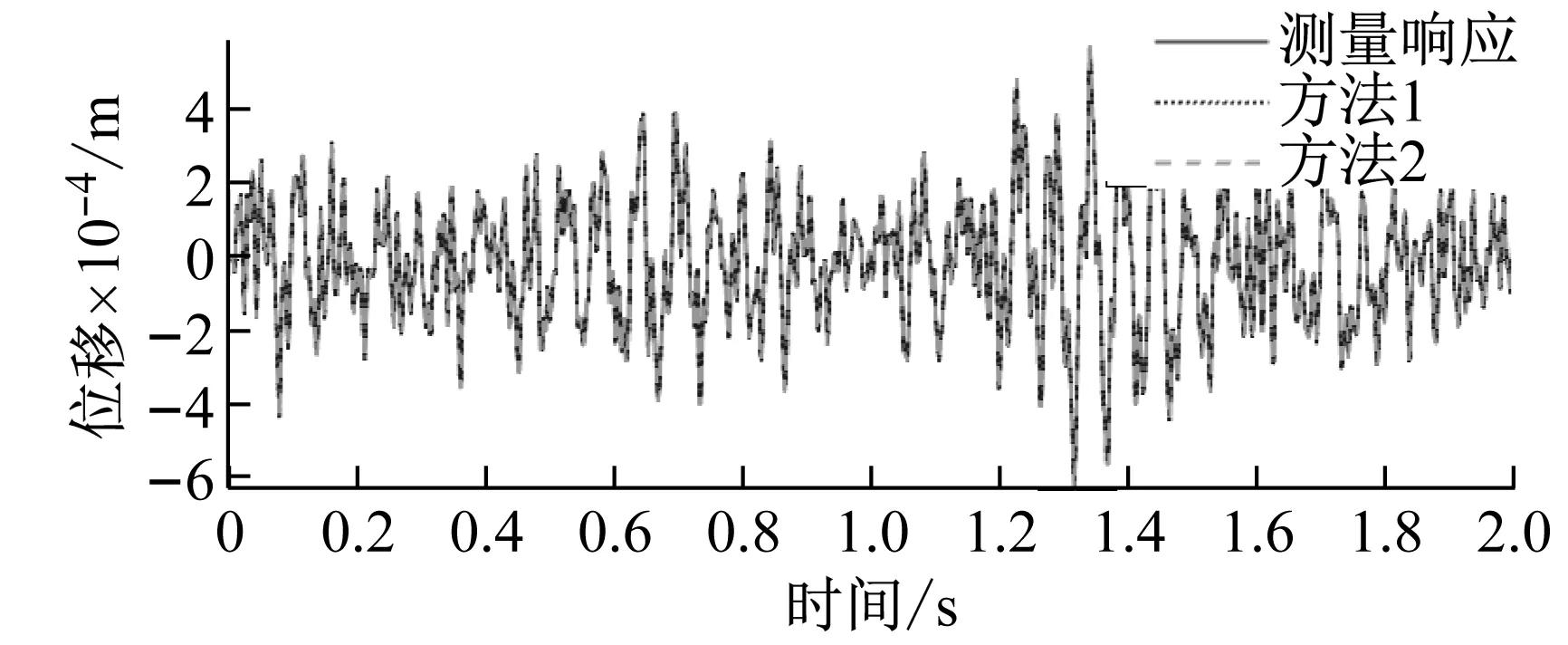
(b) 11節點Y向位移圖6 重構位移響應與測量響應對比Fig.6 Comparison of reconstructed and measured displacement responses

為比較兩種方法在重構精度上的差異，引入相對百分比誤差(relative percentage errors, RPE)來衡量精度，具體公式如下：

(33)

兩種重構方法對于傳感器缺失處的響應重構結果的RPE如表1所示，對比結果可以看出方法1的重構精度要更高。

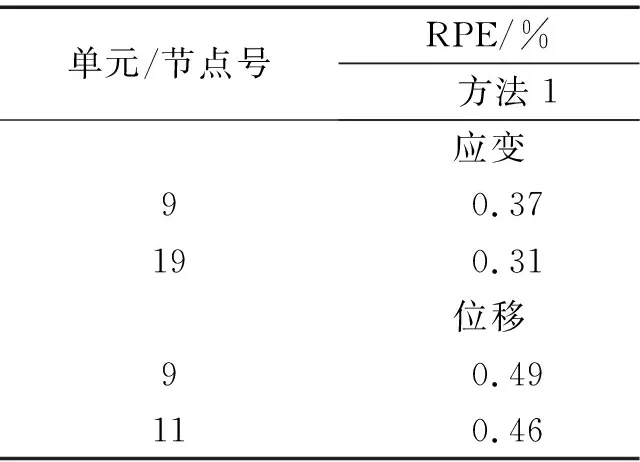
表1 相對百分比誤差Tab.1 Relative percentage errors

用RPE比較兩種方法對于其余所有位置響應的重構結果精度，結果如圖7所示。從圖7可知，方法1的應變響應重構的RPE基本都在0.4%以內，平均RPE為0.36%；位移響應重構的RPE基本都在0.5%以內，平均RPE為0.44%；方法2的應變響應重構的RPE基本在0.7%以內，平均RPE為0.48%；位移響應重構的RPE基本在0.8%以內，平均RPE為0.61%。方法1與方法2相比，由于方法1第一步已經計算出了含噪聲的各類響應，再進行粒子濾波處理時增加了狀態空間方程的觀測量，因此相比方法2，其重構精度更高。

圖7 相對百分比誤差Fig.7 Relative percentage errors

綜上分析可以看出，兩步響應重構方法可以實現對于傳感器失效處的響應和其余未安裝傳感器處的響應進行有效地重構，相比于直接使用測量響應通過濾波算法進行重構的方法重構精度更高。

為了探究在傳感器位置發生改變時，兩步響應重構方法精度是否會下降，即對測點的隨機變化是否具有一定的魯棒性，將響應測量位置改為9單元、13單元的應變響應和6節點、8節點、10節點、12節點的Y方向的位移響應，失效傳感器為10單元的應變傳感器和11節點Y方向的位移傳感器。再次進行響應重構并對比重構精度，更改測點后此方法仍能較好地對因傳感器損壞而丟失的響應進行重構，如圖8所示。對于其余所有位置的響應的重構精度并未發生較大變化，驗證了所提方法的魯棒性，如圖9所示。

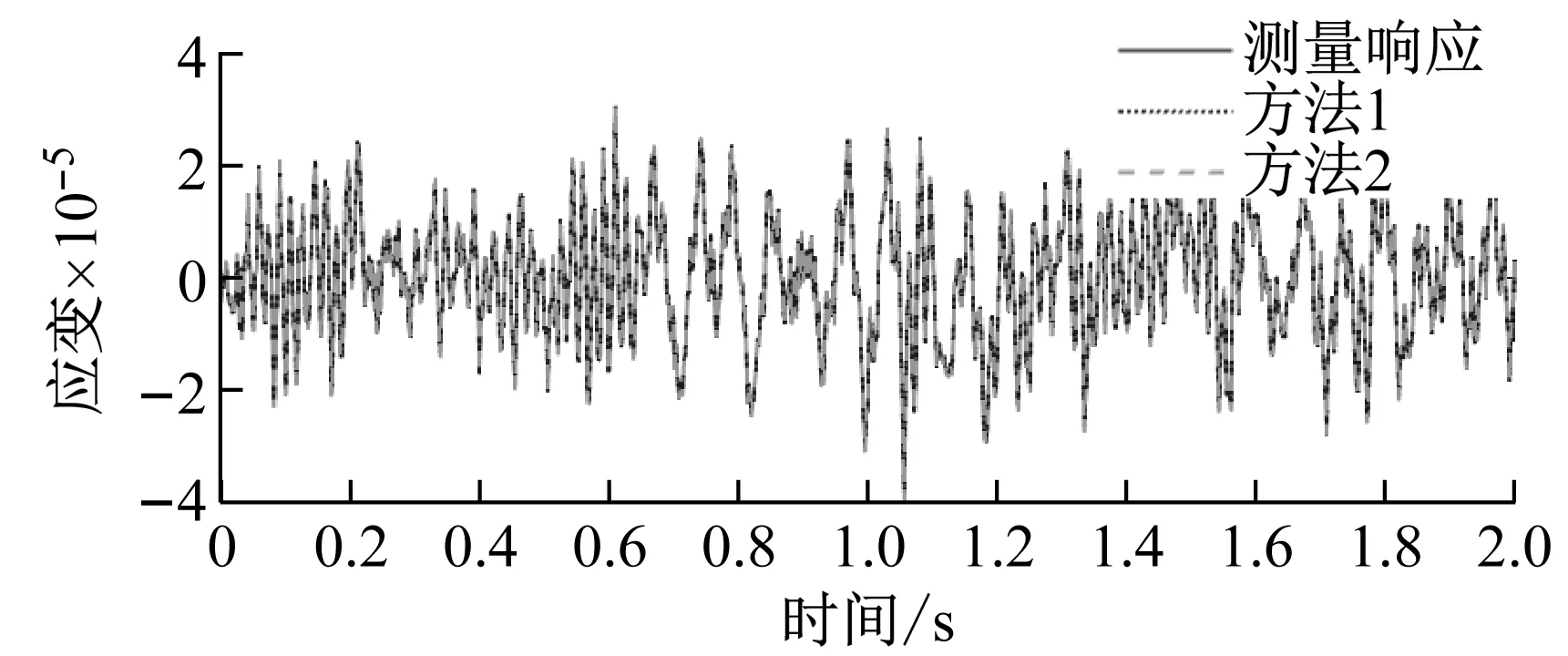
(a) 10單元應變

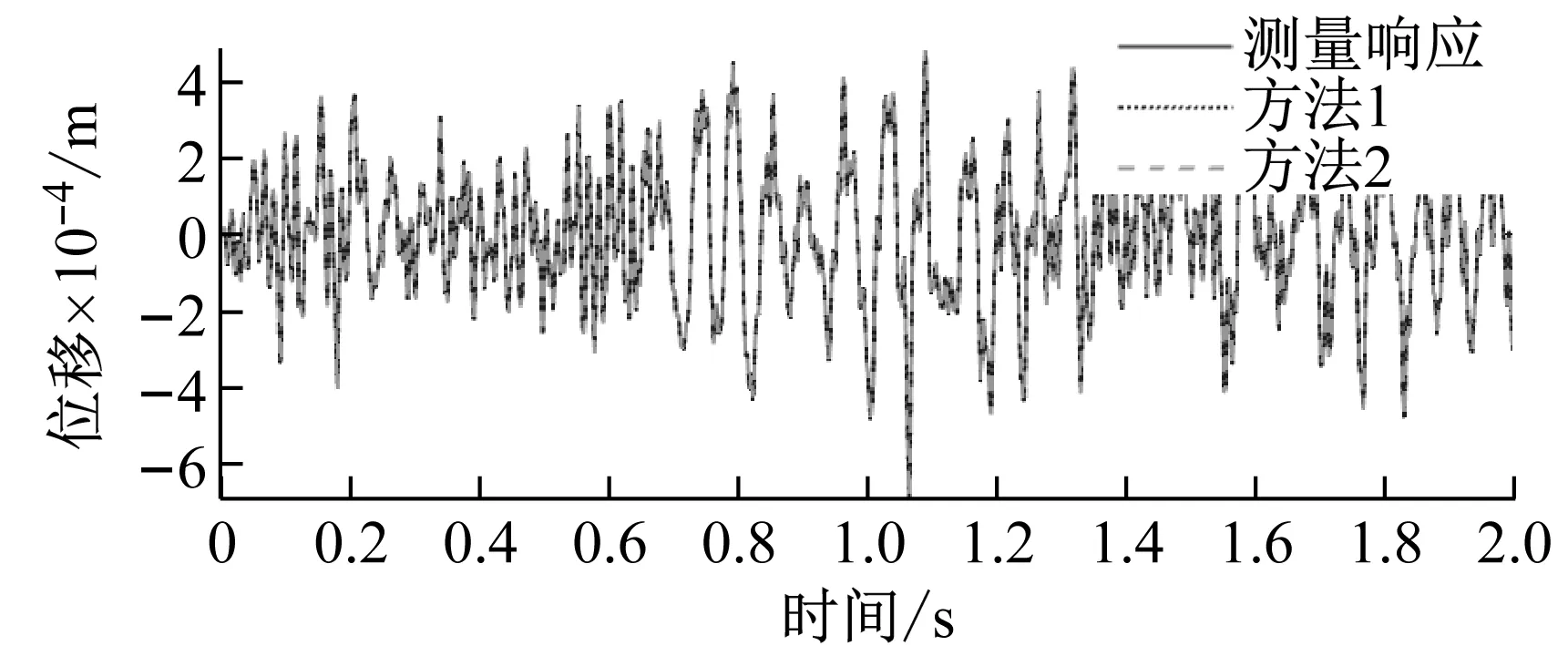
(b) 11節點Y向位移圖8 重構位移響應與測量響應對比Fig.8 Comparison of reconstructed and measured displacement responses

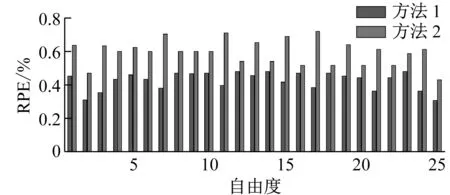
(b) 位移圖9 相對百分比誤差Fig.9 Relative percentage errors

7 結 論

研究了在傳感器損壞的情況下，利用剩余傳感器監測的包含有色噪聲的結構動態響應進行響應重構的方法。得到的結論如下：

(1) 基于有限點測量的兩步響應重構方法可在部分傳感器隨機損壞的情況下對于其余未測量的響應以及傳感器損壞處的響應進行有效重構，與直接利用測量響應進行重構的方法相比精度更高。

(2) 將螢火蟲算法引入粒子濾波算法中替代傳統重采樣過程進行結構響應重構，可有效解決粒子貧化問題，同時粒子濾波算法也能較好地處理測量數據中的有色噪聲。

(3) 傳感器位置的改變對于兩步響應重構方法的精度未造成較大影響，此方法具有較好的魯棒性。

采用了數值算例來驗證所提出的重構方法，作者正在此基礎上進一步拓展研究，將本文所提出的方法應用于現場實測的實際工程結構中，以驗證本文方法應用于工程實際中的可靠性。