神經網絡模糊PID控制半主動懸架系統

王 琳， 王文博， 錢愛文

(1.蚌埠學院 機械與車輛工程學院， 安徽 蚌埠 233030； 2.洛陽理工學院 電氣工程與自動化學院， 河南 洛陽 471023)

懸架是一個復雜的非線性系統，用來連接車輪與車架，將路面作用于車輪上的各種力及力矩傳給車架，緩和因路面不平產生的沖擊，改善汽車平順性[1]。被動懸架阻尼器無法調節，難以滿足不同工況下舒適性的要求。因此，根據不同路況調節懸架阻尼來優化汽車振動特性成了懸架領域研究的熱點之一[2-5]。模糊控制可以有效解決車輛半主動系統的多參數非線性問題，對過程參數的變化不敏感，魯棒性好，通用性強，但存在穩態誤差[6-7]；經典PID控制策略簡潔有效，可以有效消除穩態誤差[8-9]，但只適用于能夠建立精確數學模型的線性定常參數系統。將模糊控制和PID控制相結合，設計出能夠調整PID控制參數的模糊PID控制器。模糊PID控制汽車半主動懸架系統具有良好抑制擾動的能力，對多種激勵信號響應過沖量小，調節時間短，綜合性能指標好[10-12]。以車輛懸架動撓度作為控制輸入[13]，建立模糊PID控制模型，將其應用于半主動懸架數學模型，車輛的平順性得到明顯改善。PID控制器3個增益參數的確定依賴于模糊系統中模糊規則的制定，控制效果的優劣取決于研究者的經驗。文獻[14]針對車輛半主動懸架，提出一種變論域模糊PID控制方法，以解決模糊PID存在的因模糊規則制定盲目性而產生的在線調節時間過長的問題。文獻[15]采用遺傳算法優化模糊PID控制器的懸架，車身振動加速度、懸架動撓度和輪胎動載荷的均方根都有所下降，效果優于模糊PID控制。

優化車輛車身振動加速度、懸架動撓度和輪胎動載荷等參數能有效改善整車的操縱穩定性及平順性。現有的控制算法也很多，但每種算法均有局限性，難以獲得最優參數。BP神經網絡算法具有較強的函數逼近性，適合復雜非線性系統的建模與控制，但收斂慢、易陷入局部最小。本文將自適應學習算法應用于BP神經網絡，既保留了BP神經網絡算法的非線性映射及泛化能力，又克服了其不足之處。

以某轎車為研究對象，在深入分析懸架性能指標的基礎上建立二自由度1/4半主動懸架數學模型，利用模糊邏輯規則將狀態變量進行模糊化和歸一化處理，再輸入神經網絡中，BP神經網絡技術對加權系數進行調整，得到優化的PID控制參數。神經網絡模糊PID控制半主動懸架，可以實時調整PID控制器參數，改善車輛的使用性能。

1 半主動懸架動力學模型的建立

1/4半主動懸架模型如圖1所示，有2個自由度，分別為簧上質量的垂直運動和非簧載質量的垂直運動[16]。

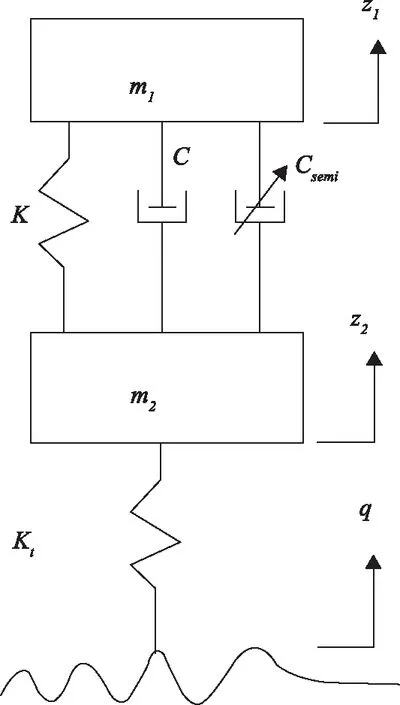
圖1 1/4半主動懸架模型

根據圖1，由牛頓定律推導出懸架運動微分方程：

(1)

(2)

式中：m1為簧上質量；m2為簧下質量；K為彈簧剛度；C為減振器阻尼系數；Kt為輪胎剛度；q為路面不平度系數；Csemi(t)為懸架的可變阻尼；z1、z2分別是車身和車輪的垂直位移。

2 半主動懸架控制器設計

神經網絡模糊PID控制器以懸架系統的偏差與偏差變化率為輸入參數，利用模糊邏輯規則將狀態變量進行模糊和歸一化處理，然后利用神經網絡自我適應和學習的特點對加權系數進行調整以優化PID控制器的3個參數KP、KI和KD。

2.1 PID控制器設計

PID控制器控制算法：

(3)

式中：u(t)為控制器輸出信號；e(t)為偏差；KP為比例增益；KI為積分增益；KD為微分增益；TI=KP/KI為積分時間常數；TD=KD/KP為微分時間常數。

結合齊格勒-尼柯爾斯規則確定出PID控制器的初始參數KP0、KI0、KD0。

2.2 模糊控制器設計

2.2.1 輸入和輸出變量值模糊化

為實現控制參數調整，需要將車身垂直速度、車身垂直加速度量化到論域{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}中，論域和模糊子集相對應，用負大[NB]、負中[NM]、負小[NS]、零[ZO]、正小[PS]、正中[PM]、正大[PB]等來表達模糊子集。模糊控制器的輸出變量為ΔKP、ΔKI、ΔKD。輸入變量和輸出變量的隸屬函數選擇高斯隸屬函數[10]：

(4)

式中：σ=0.85；c={-6，-4，-2，0，2，4，6}。根據高斯隸屬函數可求得各模糊子集的隸屬度。

2.2.2 建立模糊規則表

(1)KP值取決于系統的響應速度，增大KP可提高響應速度，減小穩態偏差，但KP值過大會產生比較大的超調，過小則響應速度減慢。故調節時KP值先增再減，最后再增加。根據上述規則，制定KP模糊規則表，如表1所示。

表1 KP模糊規則表

(2)調節初期為防止積分飽和引起較大超調，KI值要小些，甚至可以為零，調節中期考慮到系統穩定性，KI值要適中，在調節后期應增加KI值以減小調節靜差。根據上述規則，制定KI模糊規則表，如表2所示。

表2 KI模糊規則表

(3)KD值的大小對系統動態特性調節影響顯著，調節初期，增大KD值以減小超調量，鑒于調節特性對KD值變動比較敏感，調節中期適當減小KD值并保持，調節后期應減小KD值以減少調節時間。根據上述規則，制定KD模糊規則表，如表3所示。

表3 KD模糊規則表

2.3 神經網絡模糊PID控制器設計

BP神經網絡是一種按誤差逆傳播算法訓練的多層前饋網絡，包括輸入層、隱含層和輸出層[17]。輸入層有2個神經元，分別對應車身垂直速度、車身垂直加速度，輸出層有3個神經元分別對應PID控制器的3個可調參數KP、KI和KD，如圖2所示。

圖2 BP神經網絡結構圖

網絡輸入層：

(5)

網絡隱含層的輸入和輸出：

(6)

(7)

隱含層神經元的活化函數為Sigmoid函數：

(8)

網絡輸出層的輸入和輸出：

(9)

(10)

(11)

(12)

(13)

神經網絡具有出色的并行計算、信息容錯和自適應學習功能，但易陷入局部極小值，收斂慢且易引起震蕩。為克服其不足，研究采用變步長BP神經網絡算法，通過連續2次監測訓練的誤差值，根據訓練誤差的反饋做出不同的響應，動態調整學習率。誤差下降，則增大學習率；誤差在較小范圍內，則步長不變；誤差超過設定值，則減小學習率。

網絡輸出層神經元選Sigmoid函數作為活化函數：

(14)

性能指標函數：

(15)

按最速下降法修正網絡權系數，增加一個使收斂快速的全局極小慣性量，則有

(16)

式中:η為學習率；α為平滑因子。

(17)

用函數sgn[?y(k)/?u(k-1)]近似代替?y(k)/?u(k-1)。

網絡隱含層加權系數的學習算法為

(18)

(19)

式中:

g′(·)=g(x)(1-g(x))

f′(·)=(1-f2(x))/2

網絡輸出層加權系數的學習算法為

(20)

(21)

設計好網絡結構，確定出訓練算法后，可對神經網絡進行訓練。當輸出值達到預期即可停止，否則繼續進行訓練調整權值。

2.4 控制器算法設計

基于BP神經網絡模糊PID控制算法的設計流程如圖3所示。

圖3 神經網絡模糊PID控制器算法流程圖

3 仿真分析

在Matlab/Simulink模塊中建立神經網絡模糊PID控制器，并將其應用于1/4半主動懸架上，如圖4所示。將仿真結果與被動懸架和模糊PID控制半主動懸架系統進行對比。車輛仿真參數：簧上質量m1為365 kg,簧下質量m2為38 kg,彈簧剛度K為20 000 N/m,減振器阻尼系數C為1 300 ns/m,輪胎剛度Kt為180 000 N/m,懸架限位行程6.5 cm。

采用濾波白噪聲隨機路面輸入，仿真時間為100 s，仿真步長為0.01 s，車輛以60 km/h的速度在A、B、C和D級路面上行駛，選取車身垂直振動加速度、車輪動載荷、懸架動撓度作為控制策略的評價指標，仿真結果如表4所示。受篇幅限制，僅給出車輛在B級路面上的時域曲線，如圖5～圖7所示。

圖4 神經網絡模糊PID控制半主動懸架系統模型

表4 懸架性能參數仿真結果

圖5 車身垂直振動加速度仿真曲線

圖6 懸架動撓度仿真曲線

圖7 車輪動載荷仿真曲線

由表4可知，在不同等級路面上，采用神經網絡模糊PID控制策略和采用模糊PID控制策略的半主動懸架，車身垂直振動加速度均優于被動懸架。神經網絡模糊PID控制策略對車身垂直振動加速度的抑制效果最為明顯，加速度均方根降低33.33%以上。圖5顯示加速度時域信號變化平緩，最大值沒有出現惡化，神經網絡模糊PID控制的半主動懸架系統車身垂向加速度峰值均低于被動懸架和模糊PID控制半主動懸架，且系統舒適性優良。

神經網絡模糊PID控制半主動懸架的懸架動撓度均方根低于模糊PID控制半主動懸架和被動懸架，降低了5.89%以上。懸架動撓度時域信號變化平緩，隨著路面等級下降，出現了動撓度最大值大于被動懸架動撓度最大值的現象，但低于模糊PID控制策略下的半主動懸架，總體上未出現惡化現象，也未超過懸架的限位行程，充分利用了懸架設計空間，如圖6所示。

不同路面等級，半主動懸架的車輪動載荷均方根降低幅度存在差異，在A級和B級路面上，神經網絡模糊PID控制半主動懸架系統的車輪動載荷優于模糊PID控制半主動懸架和被動懸架，車輪附著能力良好，車輪動載荷時域信號變化平緩，如圖7所示。但在C級和D級路面上，神經網絡模糊PID控制策略下的半主動懸架相對半主動懸架表現略差。

綜上所述，采用神經網絡模糊PID控制的半主動懸架可以有效降低車輛的車身垂向加速度、懸架動撓度和輪胎動載荷，3個指標的時域信號變化也比較平緩，在一定程度上改善了車輛的平順性和操縱穩定性。

4 結 語

(1)神經網絡模糊PID控制策略能夠有效抑制半主動懸架系統的車身垂直振動加速度、懸架動撓度和車輪動載荷。

(2)本文提出的基于神經網絡控制策略為懸架參數優化提供一定參考，但在控制機理方面還有待進一步深入研究。