差分隱私保護下的高維數據集發布
朱 徐 亞
(安徽理工大學 計算機科學與工程學院, 安徽 淮南 232001)
近年來,個人隱私泄露問題開始引發人們的擔憂,數據隱私保護成為計算機學科的熱門領域。其中,高維合成數據集的隱私保護數據發布問題是一個巨大的挑戰。一般的高維數據集發布算法會出現計算復雜度過高的問題,若直接使用擾動策略對數據集加噪,會因為注入過多的噪聲導致數據的可用性降低。目前最流行的解決方案是采用差分隱私機制[1]。Mohammed等[2]提出了一種針對決策樹分析的差分隱私合成數據發布算法DiffGen。Chen等[3]提出了一種基于新型稀疏向量技術合成數據集的方法,結合差分隱私分析所有屬性之間的成對關系生成無向的依賴關系圖,并由此得到聯合樹模型。然而該新型向量技術中的隱私分析過程是錯誤的[4],無法實現預期的隱私保障。Li等[5]提出了一個利用高斯Copula函數的差分隱私數據合成器DPSynthesizer。Zhang等[6]提出了一種基于貝葉斯網絡的高維合成數據集生成算法PrivBayes,目前流行的GAN模型的結構化數據生成算法仍處于起步階段,存在諸多缺陷[7-8]。
為了解決PrivBayes在貝葉斯網絡建模階段使用互信息作為屬性相關性衡量標準所帶來的數據信噪比低的問題,本文提出基于差分隱私采樣機制的DPSM-Bayes算法,通過采樣機制調整數據量的大小,能夠使數據集獲得最優可用性,提出一種改進的Laplace機制替換原本的差分隱私Laplace機制,可以有效地降低在較低的概率分布上添加正的Laplace噪聲所引起的系統偏差,在隱私保護程度不變的情況下,進一步提高數據集的可用性。
1 基本概念
假設數據持有方A將數據發布給數據使用方B,數據使用方B希望從數據中學到盡可能多的知識,與此同時,A不希望B學到任何的個體信息。假設數據持有方A持有的數據集為高維列表數據集,數據集D由d個屬性或隨機變量組成,即X={X1,X2,…,Xd},數據集包含n條元組且符合獨立同分布。算法實現的目標是采用非交互式查詢框架,直接發布一個滿足差分隱私保護的脫敏的合成數據集。
1.1 差分隱私
2006年,Dwork等[9]提出差分隱私的概念,要求所發布數據集的任何信息必須要經過一個隨機化算法的處理,保障數據集中的任何一條記錄的個體信息不被泄露。差分隱私擁有嚴格的統計學定義,能夠對隱私保護水平進行量化評估。
定義1ε-差分隱私[9]:假設有隨機化算法G,O為G的任意可能輸出,若對于任意兩個至多相差一條元組的相鄰數據集D1和D2,滿足:
Pr[G(D1)=O]≤eε·Pr[G(D2)=O]
(1)
則稱算法G滿足ε-差分隱私保護。其中:參數ε為隱私保護預算;Pr[·]表示事件發生的概率。
定義2 全局敏感度[9]:設有函數f:D→Rd,輸入為一數據集,輸出為一個d維實數向量,對于任意的相鄰數據集D1和D2,
(2)
稱為函數f的全局敏感度。
定義3 Laplace機制[9]:設有函數f:D→Rd,函數的敏感度為Δf,若Y~Lap(Δf/ε)為加入的隨機噪聲,則算法G(D)=f(D)+Y滿足ε-差分隱私保護。

定義5 序列組合性[11]:設有一個隨機化算法序列G1,G2,…,Gm,算法Gi符合εi-差分隱私保護,則算法序列Gi(D)滿足(∑iεi)-差分隱私保護。
定義6 并行組合性[12]:設有一組隨機化算法G1,G2,…,Gm,算法Gi符合εi-差分隱私保護,對于任意不相交的數據集D1,D2,…,Dm,則由這些算法組成的組合算法G(G1(D1),G2(D2),…Gm(Dm))滿足(maxεi)-差分隱私保護。
1.2 貝葉斯網絡
貝葉斯網絡[13]又被稱為信念網絡,是一種概率圖型模型,是一個有向無環圖如圖1所示。對于數據集D,D中的每個屬性被表示為一個節點,數據集中屬性間的相互關系被表示為有向邊的形式。
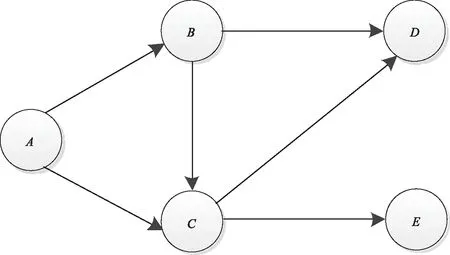
圖1 貝葉斯網絡
貝葉斯網絡為概率分布提供了一種簡潔的表示方式,可以使用貝葉斯網絡來描述概率分布中隨機變量之間的相互依賴關系,從而描述一個概率分布。假設有一個離散隨機變量集合X={X1,X2,…,Xd},貝葉斯網絡可以將它們的聯合概率分布表示為
(3)
也稱貝葉斯網絡的鏈式法則[14],貝葉斯網絡結構學習領域就是專門研究這個問題的[15]。
2 差分隱私保護下的高維數據集發布算法
針對PrivBayes算法的缺點,本文提出一種新穎的差分隱私保護下的高維數據集發布算法DPSM-Bayes,實現流程圖如圖2所示。

圖2 差分隱私保護下的高維數據集發布算法流程圖
2.1 基于采樣機制構建滿足差分隱私保護的貝葉斯網絡
為了降低計算復雜度,GreedyBayes算法將貝葉斯網絡的度k限制在一個較小的值,大大減少了時間開銷,使用互信息作為屬性間相關程度的評分函數,利用差分隱私指數機制,選擇出滿足差分隱私保護的最優父節點集,進而構造出滿足差分隱私保護的貝葉斯網絡。
相比較于互信息I的值域,互信息的敏感度是一個不小的值,當評分函數的敏感度較大時,很有可能添加的噪聲量覆蓋了原本的數據量,導致構建的貝葉斯網絡結構與數據集概率分布的擬合程度較差。因此,本文利用差分隱私采樣機制[16]滿足差分隱私保護的貝葉斯網絡構建算法SMBayes。
定義7 采樣機制[16]:設有滿足ε-差分隱私的隨機化算法G,則對于這樣的一個算法Gα:首先以概率α對輸入數據集中每條元組獨立采樣,接著對采樣得到的數據集應用算法G。則算法Gα為輸入數據集提供了ln(1+α(eε-1))-差分隱私保護。
本文提出基于差分隱私采樣機制的子算法SMBayes算法,輸入為原始數據集D、貝葉斯網絡的度k、隱私預算ε1,輸出為貝葉斯網絡N。該算法的具體描述步驟:
(1)計算采樣率α;
(2)以概率α對D中的元組采樣,得到輸入數據集D′;
(3)εα=ln(eε1-1+α)-lnα;
(4)初始化N=?,V=?;
(5)隨機選取X中的一個屬性作為貝葉斯網絡的首節點X1,將(X1,?)添加到N,將X1添加到V;
(6)fori=2 tod;
(7)初始化Ω=?;
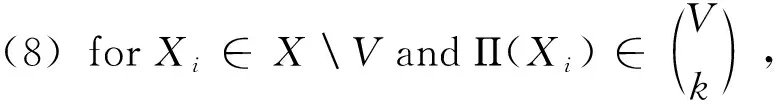
(9)對輸入數據集D′,使用差分隱私指數機制,以互信息為評分函數,隱私預算為εα/(d-1),從Ω中選出一個AP對(Xi,Π(Xi));
(10)將選出的AP對(Xi,Π(Xi))添加到N,將Xi添加到V;
(11)end for;
(12)returnN。
通過分析不同數據集大小情況下,敏感度ΔI與采樣機制的隱私預算εα之間的關系,得到采樣輸入數據集D′最佳尺寸的計算公式:
(4)
其中:1 本文提出改進的Laplace機制IMLap-Noisy算法。該算法的輸入為原始數據集D、貝葉斯網絡N、隱私預算ε2,輸出為d個滿足差分隱私保護的邊緣條件概率分布。IMLap-Noisy算法具體描述步驟: (1)初始化P*=?; (2)fori=1 tod; (3)由AP對(Xi,Π(Xi))和D實體化聯合概率分布Pr(Xi,Π(Xi)); (5)根據Pr*(Xi,Π(Xi))計算閾值t; (6)forpinPr*(Xi,Π(Xi)); (7)ifp (8)end for; (9)歸一化Pr*(Xi,Π(Xi)); (10)由Pr*(Xi,Π(Xi))得到Pr*(Xi|Π(Xi))并將其添加到P*; (11)end for; (12)returnP*; 閾值t計算是IMLaplace機制的核心,t的計算公式為 (5) 其中:t=i/1 000,i∈*且0 從邊緣分布采樣生成合成數據集的過程相對于前兩個過程較為簡單,利用貝葉斯網絡的特點,采用邏輯采樣方法[17]。每次通過一個低維條件概率分布采樣出對應的一個屬性值,作為其他屬性的父節點取值進而確定下一個屬性的值。由于貝葉斯網絡是一個有向無環圖,當我們對最后一個屬性進行采樣時,在此之前的所有屬性都已經采樣結束,即得到了一條完整的記錄。邏輯采樣可以生成任意數量的記錄,考慮到某些應用需要合成數據集與原始數據集的記錄數量相似,同時有利于在實驗評估階段對兩個數據集進行對比分析,仍然選用n作為合成數據集的大小。 實驗選用的數據集的具體描述如表1所示,選用平均變分距離和Wasserstein距離作為概率分布間的距離度量,選用SVM分類準確度作為合成數據集可用性的度量標準。 表1 實驗選用的數據集 為了評估IMLaplace機制的性能,將IMLaplace機制與原始Laplace機制進行對比,采用平均變分距離和Wasserstein距離作為加噪前后的概率分布的距離度量,評估兩種機制加入的噪聲對概率分布的影響;將由概率分布采樣出的數據集構造的支持向量機(SVM)分類器模型的分類準確度作為數據可用性的度量,一定程度上可以反映兩種加噪機制對數據集質量的影響程度。實驗中選用的數據集為Cancer、Sachs和Alarm,實驗結果均為20次實驗的平均值。實驗結果如表2和表3所示。在平均變分距離和Wasserstein距離2種度量下,IMLaplace機制都取得了比原始的Laplace機制更好的效果。 表2 平均變分距離 單位:% 表3 Wasserstein距離 單位:% 在評估2種加噪機制對數據集質量和可用性的影響,每個數據集分別選出兩個屬性作為兩組實驗的類別屬性,其他屬性作為特征屬性,構造SVM分類器模型,將原始數據集的20%作為測試集,驗證2種機制下的分類準確度。隱私預算ε設置為0.01~1.6,結果如圖3~圖5所示。NoLaplace表示不對概率分布進行Laplace加噪處理,在圖中作為基準分類準確度。 (a) Cancer Y=Smoker (b) Cancer Y=Cancer (a) Sachs Y=Mek (b) Sachs Y=Raf (a) Alarm Y=LVEDVolume (b) Alarm Y=TPR 隨著隱私預算ε的增加,不同數據集上屬性的分類準確度均逐漸增大因為隱私預算增加時,對數據的隱私保護程度降低,對數據添加的噪聲擾動較少,數據集的質量和可用性提高。當隱私預算ε的值較小時,能夠看到IMLaplace機制得到的數據集的分類準確度明顯高于Laplace機制,并且隨著隱私預算ε的增加,兩者之間的差距呈現逐漸縮小的變化趨勢,直到接近基準分類準確度,因為在隱私預算ε的值較小的情況下,Laplace機制添加的噪聲值較大的概率最高,對較低的概率值添加正噪聲的概率也最高,IMLaplace機制能夠很好地解決該問題。 為了驗證和評估DPSM-Bayes算法的性能優越性,選用PrivBayes算法作為對照組,分別讓兩種算法輸出的合成數據集執行分類任務,選用SVM分類器作為分類模型,通過分類準確度驗證兩種算法生成的數據集的質量和可用性,如圖6和圖7所示。 隨著隱私預算ε的增加,在NLTCS和ACS兩個數據集上的分類準確度均逐漸增加,表明隱私保護程度和數據的可用性是矛盾的,隱私保護程度越高,數據集的可用性就越低。因此,在實際應用中要在隱私保護程度和數據可用性之間尋求一個平衡點。另外,相對于NLTCS數據集,ACS數據集上2種算法的分類準確度與基準分類準確度的距離明顯更大。在圖6和圖7中,DPSM-Bayes算法生成數據集的分類準確度均高于PrivBayes算法的分類準確度,表明DPSM-Bayes算法生成的數據集的質量和可用性明顯優于PrivBayes算法。 (a) NLTCS Y=Outside (b) NLTCS Y=Bathroom (a) ACS Y=Mortgage (b) ACS Y=School 為了解決隱私保護高維數據集發布中存在的計算復雜度高和數據可用性低的問題,針對PrivBayes算法的缺陷,提出了DPSM-Bayes算法,優化了互信息敏感度過高帶來的信噪比低的問題,利用差分隱私采樣機制選取更合適的數據集尺寸,從而緩解該問題。本文還提出了更適合于高維數據分布加噪的IMLaplace機制,能夠有效地緩解由于在較低的概率值上加入正噪聲所帶來的誤差。在相同的隱私保護程度下,DPSM-Bayes算法在數據生成質量和可用性上明顯優于PrivBayes算法,實現了隱私保護高維數據集發布在隱私性和可用性之間的平衡。2.2 基于改進的Laplace機制對邊緣分布加噪
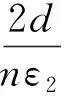
3 實驗評估

3.1 IMLaplace機制的性能





3.2 DPSM-Bayes算法的性能


4 結 語

