基于組合預(yù)測(cè)方法的鄭州市貨運(yùn)周轉(zhuǎn)量預(yù)測(cè)研究
徐燁昕, 陸 芬
(武漢科技大學(xué) 管理學(xué)院, 湖北 武漢430070)
隨著電子商務(wù)和共享經(jīng)濟(jì)的進(jìn)一步發(fā)展,物流的重要性逐漸提高,專(zhuān)業(yè)化和社會(huì)化促進(jìn)了各行業(yè)物流需求的增長(zhǎng)。鄭州商貿(mào)流通的迅速發(fā)展,國(guó)內(nèi)外大型商貿(mào)流通企業(yè)先后入駐鄭州,大市場(chǎng)、大流通格局的逐漸形成,隨著帶動(dòng)了物流業(yè)的快速發(fā)展。截止到2020年,鄭州市的貨運(yùn)周轉(zhuǎn)量、貨物量以及業(yè)務(wù)總量都呈現(xiàn)持續(xù)增長(zhǎng)的態(tài)勢(shì),物流需求規(guī)模悄然發(fā)生變化,物流服務(wù)供需更加不穩(wěn)定,無(wú)法有效評(píng)估物流需求。因此,建立有效數(shù)學(xué)模型確定物流需求顯得尤為重要。
李偉瑩等[1]建立了灰色預(yù)測(cè)模型,探討了我國(guó)水產(chǎn)品物流需求,并從技術(shù)、渠道、人才、政策等方面提出了相關(guān)建議。吳家麒等[2-3]通過(guò)建立改進(jìn)的灰色馬爾可夫鏈模型,對(duì)目標(biāo)城市的物流需求(貨運(yùn)量)進(jìn)行了定量預(yù)測(cè),得到了更準(zhǔn)確的結(jié)果。張雪[4]基于GM(1,1)模型對(duì)河北省冷鏈物流需求進(jìn)行了定量預(yù)測(cè)。黃建華等[5-6]基于ARIMA模型的組合預(yù)測(cè)方式,能有效提高預(yù)測(cè)精度。姜云璐等[7]將灰色預(yù)測(cè)模型運(yùn)用到山區(qū)土地利用時(shí)空變化方面。韓正超等[8]認(rèn)為,物流需求是經(jīng)濟(jì)發(fā)展產(chǎn)生的衍生需求,是經(jīng)濟(jì)發(fā)展的產(chǎn)物。在組合預(yù)測(cè)方法[9-11]中,灰色預(yù)測(cè)模型同樣是研究熱點(diǎn)。指數(shù)平滑法[12]在預(yù)測(cè)方法中利用率也很高。鄭偉倫[13]利用指數(shù)法預(yù)測(cè)江西省GDP,可以更好地檢測(cè)數(shù)據(jù)的波動(dòng)性。
系統(tǒng)預(yù)測(cè)的方法有很多,包括線性回歸預(yù)測(cè)法、指數(shù)平滑預(yù)測(cè)法、彈性系數(shù)預(yù)測(cè)法、灰色預(yù)測(cè)法等。灰色預(yù)測(cè)法和指數(shù)平滑預(yù)測(cè)法都可以利用Excel表格軟件進(jìn)行計(jì)算,但灰色預(yù)測(cè)法不需要很多的數(shù)據(jù)就可以對(duì)目標(biāo)進(jìn)行結(jié)果預(yù)測(cè)。本文采集鄭州市經(jīng)濟(jì)社會(huì)發(fā)展的主要統(tǒng)計(jì)指標(biāo)(貨運(yùn)周轉(zhuǎn)量),使用改進(jìn)灰色預(yù)測(cè)法和二次指數(shù)平滑法對(duì)鄭州市未來(lái)5年的綜合貨運(yùn)量做出合理預(yù)測(cè)。
1 鄭州市貨運(yùn)周轉(zhuǎn)量預(yù)測(cè)分析
1.1 基礎(chǔ)數(shù)據(jù)
貨運(yùn)需求量采用地方統(tǒng)計(jì)局的實(shí)際數(shù)據(jù),如表1所示。
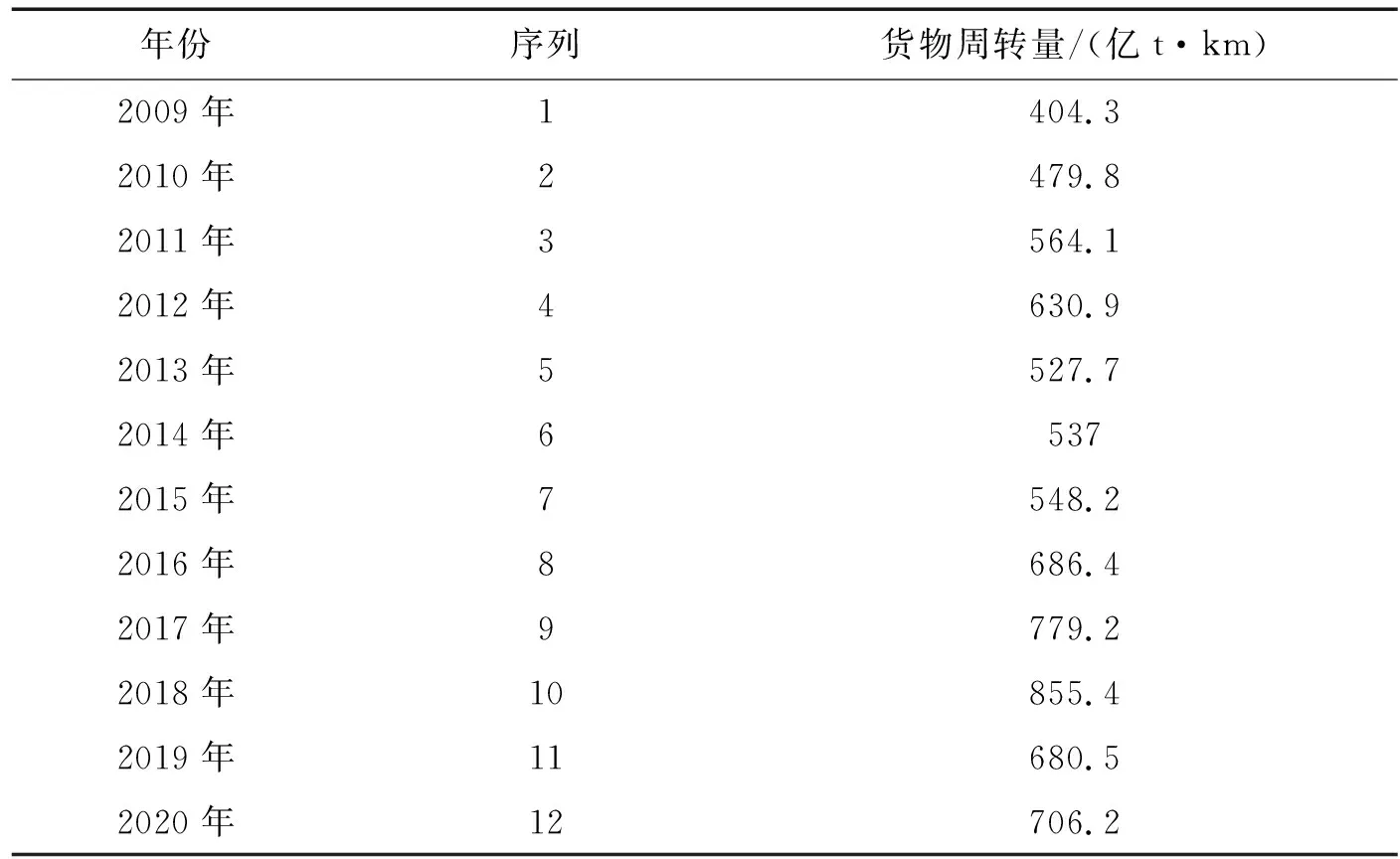
表1 鄭州市貨運(yùn)周轉(zhuǎn)量與主要經(jīng)濟(jì)指標(biāo)數(shù)據(jù)
1.2 灰色預(yù)測(cè)法數(shù)據(jù)檢驗(yàn)
為保證建模方法的可行性,需要對(duì)原始數(shù)據(jù)做必要的檢驗(yàn)處理。設(shè)已知的原始數(shù)據(jù)為
x(0)=[404.3,479.8,564.1,630.9,527.7,537,548.2,686.4,779.2,855.4,680.5,706.2]。
計(jì)算數(shù)據(jù)的可容覆蓋為Θ=(0.857 403 919,1.153 564 995)。對(duì)原始數(shù)據(jù)進(jìn)行序列級(jí)比計(jì)算,得到序列級(jí)比數(shù)據(jù),如表2所示。
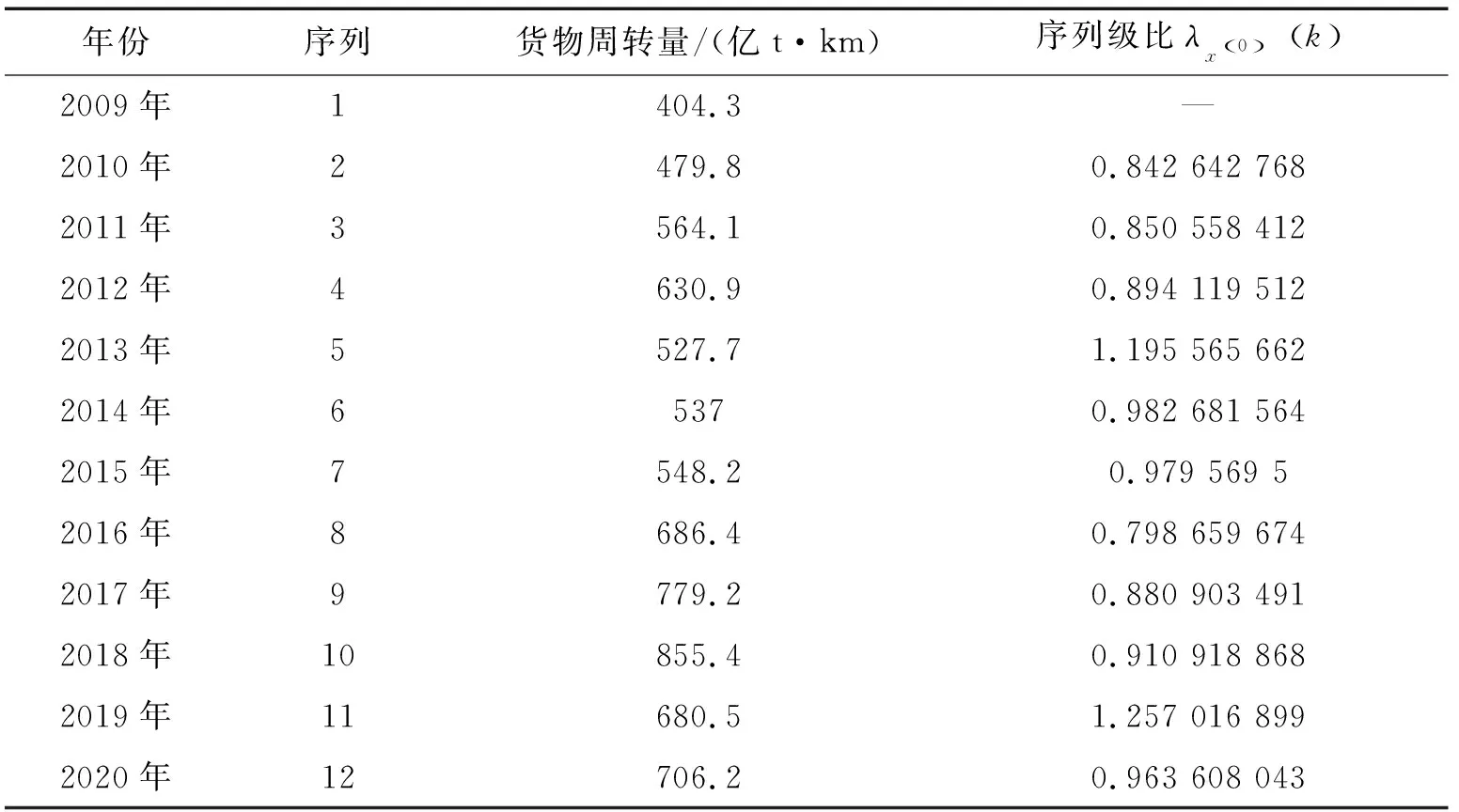
表2 灰色預(yù)測(cè)法對(duì)原始數(shù)據(jù)進(jìn)行序列級(jí)比
從表2可以看出,原始數(shù)據(jù)中序列中的級(jí)比基本都超出了可容覆蓋Θ=(0.857 403 919,1.153 564 995)的范圍,沒(méi)有被覆蓋。需要對(duì)原始數(shù)據(jù)序列x(0)進(jìn)行相應(yīng)的平移變換,保證序列級(jí)比在可容覆蓋之內(nèi)。通過(guò)累加平移變換,最終得到數(shù)據(jù)序列
z(0)=[904.3,979.8,1064.1,1130.9,1027.7,1037,1048.2,1186.4,1279.2,1355.4,1180.5,1206.2],
此時(shí)全部序列級(jí)比都達(dá)到了可容性覆蓋。
平移變換后得數(shù)據(jù)序列z(0),符合灰色預(yù)測(cè)的建模條件,取變換過(guò)后的數(shù)據(jù)序列作為初始研究序列建立灰色預(yù)測(cè)GM(1,1)模型。
1.3 指數(shù)平滑法指標(biāo)選擇
平滑系數(shù)α的選擇是預(yù)測(cè)趨勢(shì)值是否能符合實(shí)際值的關(guān)鍵。α值越大,近期需求所占權(quán)重越大;α值越小,歷史數(shù)據(jù)所占權(quán)重越大。一般遵循如下標(biāo)準(zhǔn):
(1)如果希望消除季節(jié)波動(dòng)對(duì)時(shí)間序列的影響,反映時(shí)間序列的長(zhǎng)期趨勢(shì)規(guī)律,可以選擇較小的α值,一般取0.1~0.3之間。減少修正幅度,使新數(shù)列中包含較多的原始數(shù)據(jù)信息,有利于增強(qiáng)預(yù)測(cè)結(jié)果的可信度。
(2)當(dāng)原始數(shù)列波動(dòng)較大時(shí),α應(yīng)選擇適中一些的數(shù)值(0.3~0.5)。
(3)希望能盡快反應(yīng)觀測(cè)值的變化,且原數(shù)列波動(dòng)很大、趨勢(shì)也較明顯時(shí),可以選取較高的α值,一般在0.6~0.8之間。有利于增加模型的準(zhǔn)確度,使預(yù)測(cè)結(jié)果迅速跟上歷史數(shù)據(jù)的變動(dòng)水平。
2 鄭州市貨運(yùn)需求預(yù)測(cè)研究
2.1 灰色預(yù)測(cè)法
使用累加平移變換后得數(shù)據(jù)序列z(0),利用Excel表格建立模型并對(duì)數(shù)據(jù)進(jìn)行分析。通過(guò)計(jì)算與檢驗(yàn),得到最終的預(yù)測(cè)數(shù)據(jù)與誤差值,如表3所示。
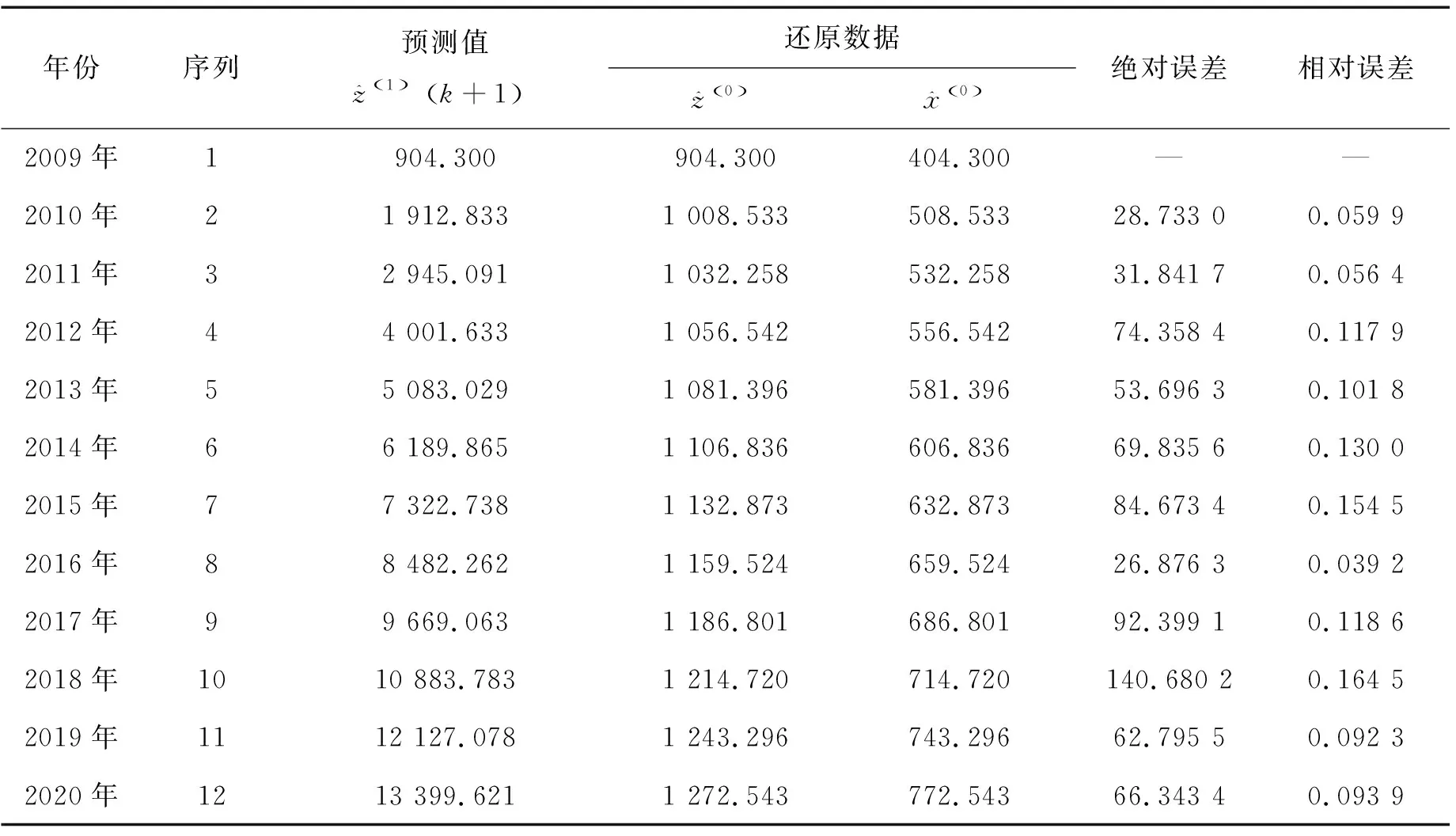
表3 灰色預(yù)測(cè)法的最終預(yù)測(cè)結(jié)果
2.2 指數(shù)平滑預(yù)測(cè)法
2.2.1 指數(shù)平滑預(yù)測(cè)法原理
二次指數(shù)平滑法的計(jì)算公式為:
(1)
Yt+T=at+bt·T
(2)
(3)
(4)
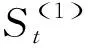
2.2.2 數(shù)據(jù)預(yù)測(cè)
根據(jù)平滑系數(shù)的選擇原則,為了消除原始數(shù)據(jù)較大的波動(dòng)值,也由于原始數(shù)據(jù)的時(shí)期較長(zhǎng)。最終選擇0.3作為初始平滑系數(shù),進(jìn)行二次平滑預(yù)測(cè),最終得出的預(yù)測(cè)值與誤差值,如表4所示。
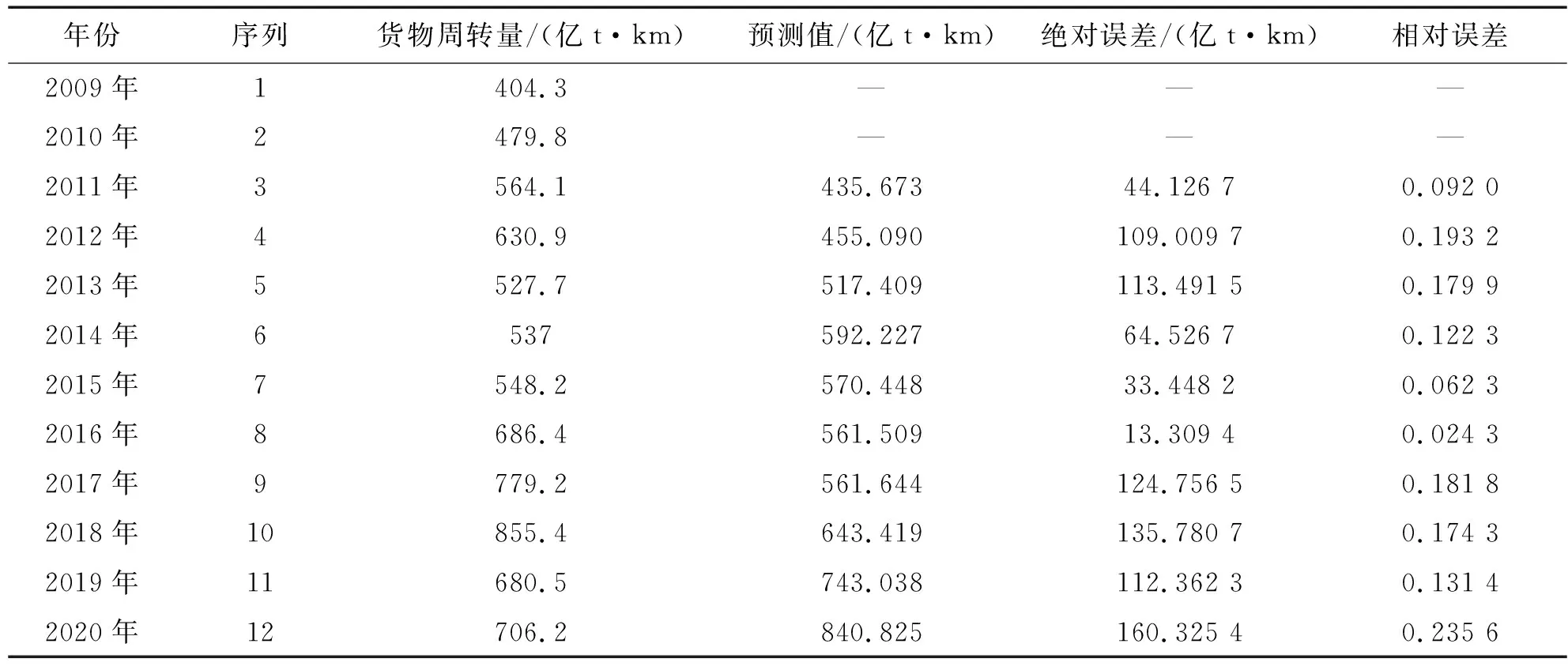
表4 平滑系數(shù)α=0.3時(shí)貨物量預(yù)測(cè)結(jié)果
為保證預(yù)測(cè)的準(zhǔn)確性,利用Excel表格中的模擬運(yùn)算表,對(duì)0.01~0.99之間的所有平滑系數(shù)α可能取值進(jìn)行模擬運(yùn)算,求出MES最小值為9 962.816 123,進(jìn)行篩選,得出了最優(yōu)平滑系數(shù)α值是0.26。
使用模擬運(yùn)算表求出的最優(yōu)平滑系數(shù)α值重新進(jìn)行預(yù)測(cè),結(jié)果如表5所示。
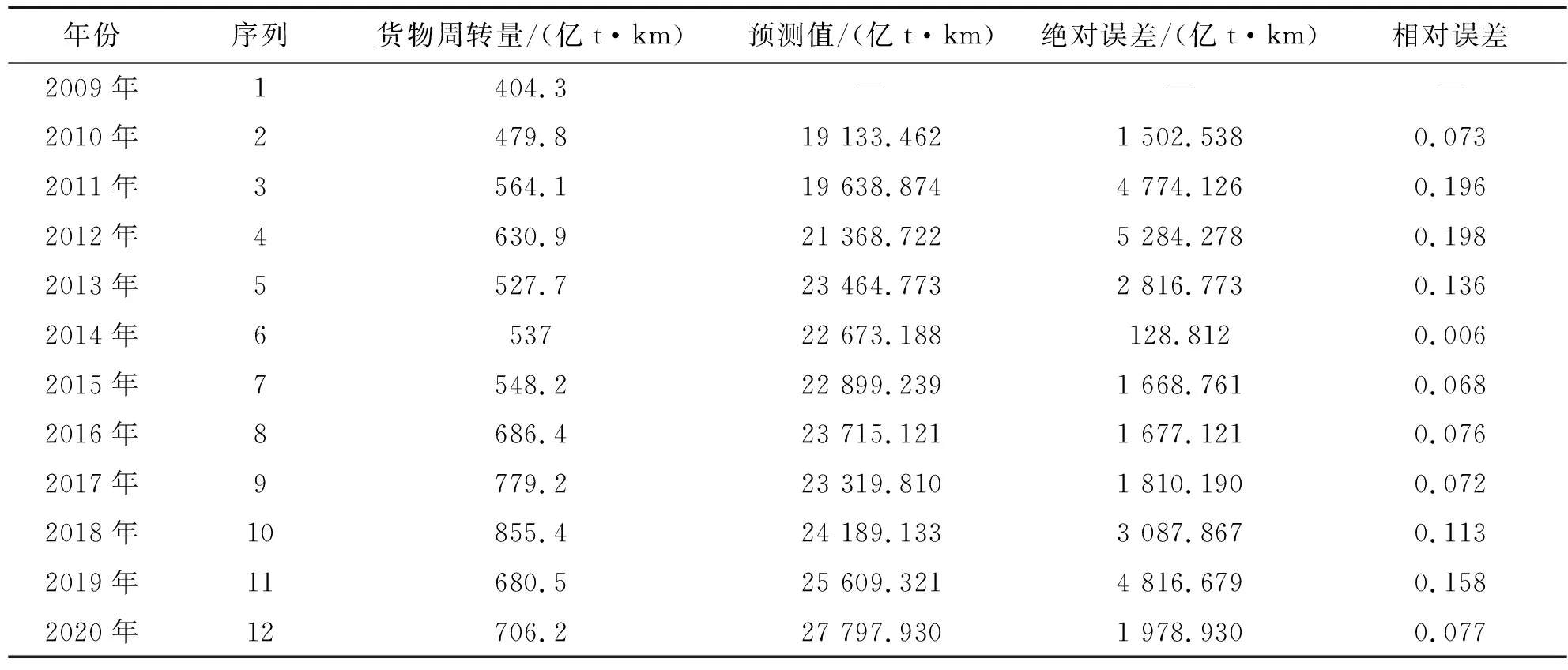
表5 平滑系數(shù)α=0.26時(shí)貨物量預(yù)測(cè)結(jié)果
為驗(yàn)證兩次不同的平滑系數(shù)取值,將兩次的相對(duì)誤差進(jìn)行對(duì)比,如圖1所示。觀察折線圖的高低起伏,當(dāng)平滑系數(shù)值為0.26時(shí)的相對(duì)誤差要明顯小于平滑系數(shù)值為0.3時(shí),最終取平滑系數(shù)值為0.26時(shí)的預(yù)測(cè)數(shù)據(jù)作為最終研究數(shù)據(jù)。

圖1 兩次平滑系數(shù)的誤差對(duì)比圖
2.3 綜合對(duì)比
用兩種方式分別對(duì)鄭州市的貨物吞吐量進(jìn)行了預(yù)測(cè),將兩組數(shù)據(jù)進(jìn)行對(duì)比分析,如表6所示。

表6 兩種預(yù)測(cè)方法的預(yù)測(cè)值與相對(duì)誤差
為了更清晰的體現(xiàn)兩種方法的預(yù)測(cè)數(shù)據(jù),對(duì)原始數(shù)據(jù)與預(yù)測(cè)數(shù)據(jù)進(jìn)行對(duì)比,如圖2所示。

圖2 兩種預(yù)測(cè)結(jié)果與原數(shù)據(jù)對(duì)比
由圖3可以清晰地看到指數(shù)平滑法數(shù)據(jù)、灰色預(yù)測(cè)法數(shù)據(jù)和原數(shù)據(jù)之間都具有一定的誤差。但是,通過(guò)指數(shù)平滑法預(yù)測(cè)出來(lái)的數(shù)據(jù),相比于原始數(shù)據(jù)沒(méi)有太多的滯后性,且較為敏感。最終選用指數(shù)平滑法對(duì)鄭州市未來(lái)5年的貨物周轉(zhuǎn)量進(jìn)行預(yù)測(cè)。
2.4 最終預(yù)測(cè)值
使用指數(shù)平滑法,選取最后一次(即2020年)計(jì)算得到的a、b值作為常量,帶入公式(2),即:Yt+T=746.784+19.718 124 9·T,得到了未來(lái)5年(2021~2025年)的最終預(yù)測(cè)值,如表7所示。
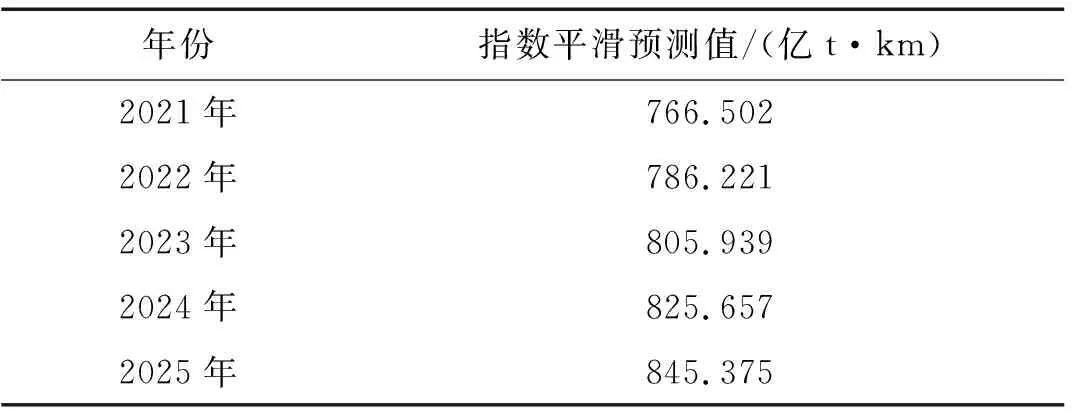
表7 鄭州市未來(lái)5年的貨物周轉(zhuǎn)量預(yù)測(cè)值
鄭州市2021年~2025年的五年的貨物周轉(zhuǎn)量的預(yù)測(cè)值分別為766.502億t·km、786.221億t·km、805.939億t·km、825.657億t·km、845.375億t·km。
3 結(jié) 語(yǔ)
鄭州物流業(yè)的發(fā)展方向應(yīng)結(jié)合國(guó)家政策和河南省的具體經(jīng)濟(jì)發(fā)展水平,一方面滿足物流供需平衡,另一方面要實(shí)現(xiàn)物流的發(fā)展和服務(wù)質(zhì)量的提高。

