基于格子Boltzmann 方法的二維氣泡群熟化過程模擬*

陳效鵬 馮君鵬 胡海豹? 杜鵬 王體康

1) (西北工業大學航海學院,西安 710072)

2) (浙江大學航空航天學院,杭州 310027)

1 引言

Ostwald 熟化現象是自然和工業界廣泛存在的現象之一,主要指在熱力學局部平衡狀態下顆粒、液滴或者氣泡群體系為了進一步降低系統的表面能,而自發地對氣泡尺度分布進行調整;發生大顆粒不斷增長,小顆粒減小直至消失的現象[1,2].生活中長期在冷凍環境下儲存的冰激凌的口感會變硬、長期靜置的自來水中會出現小氣泡,這些過程均包含了熟化機理.工業生產中也采用熟化機理解釋和控制金屬凝固過程中固態晶粒的長大[3,4]、Ouzo 雞尾酒的乳化過程[5],以及地下油藏中CO2的聚集[6]等.

對Ostwald 熟化現象的理論研究始于Lifshitz和Slyozov 提出的擴散機制主控的控制方程,并進一步給出了漸近解.幾乎同時,Wagner[1]提出了相變主控的數學描述,簡稱為LSW 理論體系.此后,針對該理論體系中要求顆粒分散度大、溶質在連續相中分布均勻等假設的局限性,眾多學者提出更新的模型,使理論成果能被進一步應用于實際問題.Ardell[7]提出特殊半徑法,對顆粒發展的相互影響展開了討論;Voorhees 和Glicksman[8]采用點源和點匯模型刻畫顆粒對環境濃度的影響,理論探討了顆粒體積有限條件下的熟化過程.這些研究是對LSW 理論的重要促進.與理論同步發展的是實驗研究.Bender 和Ratke[3]對熔融Cu-Co 合金中富Co 固體顆粒的熟化行為進行了測試,其中Co 顆粒體積分數在25%—70%之間;Alkemper 等[4]則實驗觀測了熔融Pb-Sn 合金中的富Sn 固體顆粒的長大過程,并將結果與多種理論模型進行了對比.實驗研究一方面證實了理論模型,并為理論體系的完善提供了方向;另一方面也有力地支撐了生產技術的發展.近幾十年,數值模擬被逐漸應用于Ostwald 熟化研究.Fan 等[9]采用相場方法對熟化過程進行了模擬,所獲得的顆粒形貌與實驗觀測相仿,并且顆粒群形貌特征參數演化的標度律關系與理論結果一致.Li 等[10]和Wang 等[11]數值研究了初始半徑分布對圓形顆粒的熟化過程的影響,獲得了顆粒增長的標度律關系,同時也探討了數值結果與理論預測的偏差問題.Moats 等[12]采用晶粒相場模型,開展了液-固體系的熟化過程研究,他們除了驗證了經典標度律關系,同時基于數值結果分析了體系熵的演化.Watanab 等[13,14]采用分子動力學方法對蒸氣泡群的熟化過程開展了研究,發現隨著溫度的提升熟化主控因素由相變速率轉變為擴散速度.目前,數值模擬研究正成為構建理論體系的重要一環.

格子Boltzmann 方法 (lattice Boltzmann method,LBM)是基于格子氣自動機方法發展起來的一種流體動力數值方法,其本質是對Boltzmann方程的一種離散求解方法[15,16].通過進一步與湍流模型、熱傳導方程、電磁學方程等耦合,LBM 已經被成功應用于多種復雜流動現象的模擬上.LBM多相流模型及計算是該領域比較活躍的一支,其中以Shan-Chen 模型[17]最為引人注目,且歷久彌新.通過引入分子間作用力模型,LBM-Shan-Chen 模型成功實現了多相流體的相分離模擬,且在密度比、表面張力等關鍵參數上,模擬結果與理論預測一致,關鍵是該模型反映了兩相分離的物理本質.通過與經典狀態方程相耦合,Yuan 和Schaefer[18]進一步推進了LBM 與現有熱力學體系的融合,同時也擴大了其能捕捉的多相系統密度比,提高了數值穩定性.Huang 等[19]對LBM 多相流計算過程中,體積力的施加方法、熱力學參數影響的細節開展了對比研究,為后期的數值參數的選取提供了依據.前期研究中,人們致力于LBM 模擬能力的提升及采用LBM 對典型多相流現象開展機理研究[15].

相比而言,采用LBM 進行相變機理以及流動現象的研究偏少.Chen 跟合作者[20,21]采用LBM對空化氣泡、氣泡群的演化過程進行了模擬研究.他們發現,LBM 對空泡動力學的模擬與Rayleigh-Plesset 方程預測一致.Shan 及合作者[22,23]研究了壁面潤濕性、熱效應對空泡潰滅的影響.對于相變因素更為重要的過程,Li 等[24]利用LBM 模擬了沸騰過程,準確捕捉到了流動模態的轉換過程;Shen等[25]則研究了壁面浸潤性對凝結過程的影響;Chang 等[26]利用LBM 開展了壁面結構對沸騰影響以及強化傳熱效果的研究,探討了其中流-熱耦合的力學機理.前述研究和分析中盡管涉及相變過程,但多采用了相變速率無限快這一假設.對于一些特殊情況,如Ostwald 熟化、氣泡高速振蕩等,該假設無疑會引起一定誤差.

本文采用LBM-Shan-Chen 多相流模型,對蒸氣泡群相變速率主控的Ostwald 熟化過程開展了模擬研究.探討了不同物理參數對典型氣泡群體系演化過程及相變速率的影響.結合LSW 熟化理論,驗證了數值方法的準確度;數值結果同時也表明,蒸氣泡系統的演化過程中水動力學因素有明顯的影響,這使得熟化過程具有一些有別于經典熟化過程的特點.

2 數值模型與熟化理論

2.1 LBM 多相流模型

LBM 是近年來迅速發展起來的一種流體動力學數值模擬方法.因其具有明確的微觀粒子動理學基礎,可以對較為復雜的多相流動現象進行模擬[27].本文采用Bhatnagar-Gross-Krook (BGK)單松弛Shan-Chen 多相流模型開展模擬[17].LBM控制方程為

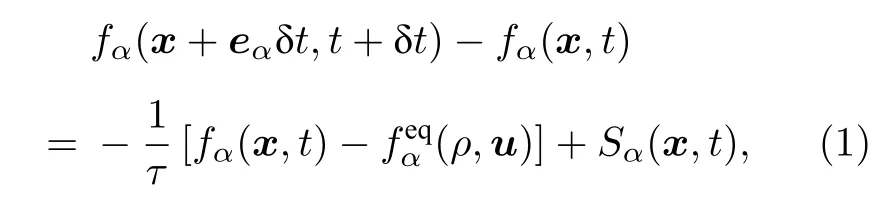
式中,fα表示時刻t、坐標x處、具有微觀速度eα的粒子分數,即密度分布函數.流體的局部密度表示為局部動量表示為ρu=本文采用LBM-D2Q9模型[16],認為二維空間中粒子具有9 種可能的離散速度,α=0,1,···,8.(1)式左端表示顆粒的遷移運動:在一個時間步 δt(=1) 中,顆粒從x跳躍到x+eαδt.D2Q9 模型中格點上的離散速度表示為

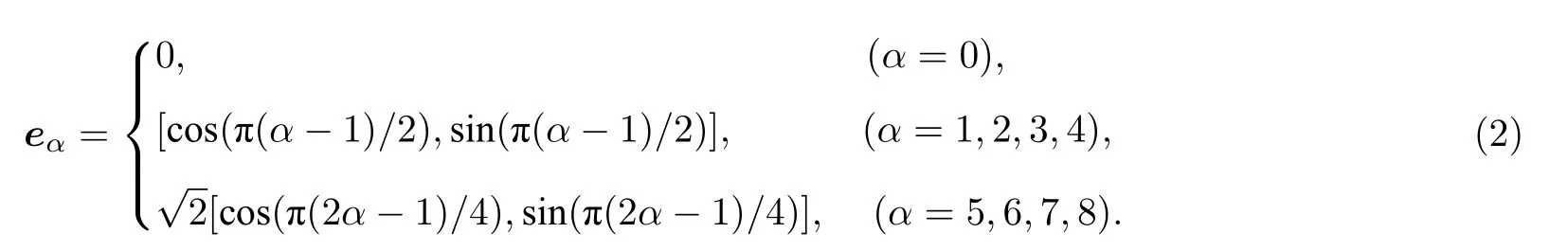
(1)式中等號左邊第一項表示碰撞作用.在準平衡態條件下,顆粒的碰撞導致其在速度相空間的分布趨于Maxwell 分布,該項中τ表示碰撞的弛豫時間.其中為Maxwell 分布函數在相空間中的離散形式,

式中cs是聲速 (D2Q9 模型中的cs=);ωα是加權系數:ω0=4/9,ω1-4=1/9,ω5-8=1/36 .

LBM 控制方程中,Sα表征了外力作用對粒子分布函數的影響,可以是長程的體積力作用,也可以是短程的分子間作用.本文采用Kupershtokh作用力模型[19]獲得作用力在微觀粒子速度方向上的“投影”,

其中F表示(外力矢量.)相應的流體局部宏觀速度表示為Huang 等[19]對比了Guo 作用力模型和Kupershtokh 作用力模型,發現相對于Guo 等提出的作用力模擬,Kupershtokh 作用力模型具有密度捕捉準確、數值穩定性好的特點.Shan 和Chen 通過與密度相關的勢函數ψ來構造分子間的不平衡作用力:

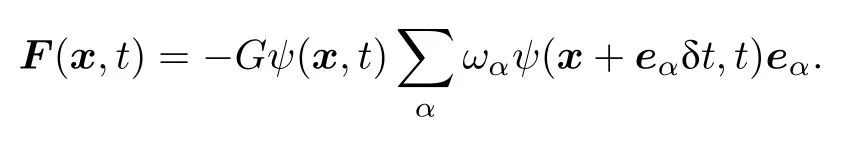
給定介質的狀態方程,當地勢函數可以表達為

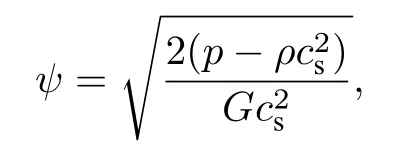
其中G為常數.本文采用Carnahan-Starling 狀態方程確定p(ρ) 關系:

其中,a=0.4963(RTc)2/pc,b=0.18727RTc/pc.本文重點取a=1,b=4,R=1 開展計算,由此得到臨界密度和臨界溫度:ρc=0.1136,Tc=0.0943 .將Sα代入LBM 控制方程,可以實現非理想氣體流動的模擬,并且可以捕捉到介質的相變過程[20,22,24].

2.2 Ostwald 熟化理論

1958 年Lifshitz 和Slyozov[28]對擴散控制的熟化進行了機理研究,他們首先數學描述了析出顆粒群在溶液中的生長過程:引入描述粒子半徑分布的函數F(R,t) (R為粒子的半徑,t為時間),并建立了演化方程.Wagner 進一步對反應主控與擴散主控的熟化過程進行了研究,從而建立了描述顆粒群熟化過程的LSW 理論體系[1,2].該理論體系由動理學方程、連續性方程和質量守恒方程組成.動理學方程刻畫了單個顆粒的增長規律,其包含“溶質”在連續相中的遷移與析出過程的數學描述為

其中,ks表征了相變速率,Rc為顆粒臨界半徑,C為溶液中溶質濃度.(4)式顯示Ostwald 熟化過程中,當析出顆粒尺度小于臨界尺度時,會逐漸消融,反之則長大.Rc與析出相在環境流體中的溶解濃度、析出相表面張力能量有關.臨界尺度可以通過下面的公式計算獲得:

連續性方程描述了粒子半徑分布函數的演化規律:

即具有半徑R的顆粒數(FdR)隨時間的變化率,取決于氣泡的增長:該表達式假設顆粒在熟化過程中沒有發生合并或分裂現象.質量守恒方程規定了析出相的總體積不變,即

(4)式—(7)式中,假設析出相顆粒是半徑為R的圓形 (二維).

本文針對反應控制熟化過程開展研究,即“溶質”在連續相中擴散得足夠快,(4)式中相變過程成為制約顆粒生長的主要因素,擴散方程可以忽略.Lifshitz 和Pitaevskii[28]在數學上推導了t →∞時擴散主控熟化過程中,顆粒尺寸等參數增長的標度律.參考Watanabe 等[14]采用的標度律推導過程,可以得到二維條件下的蒸氣泡群幾何特征參數演化規律 (附錄A):

同時,分布函數演化滿足相似關系:

其中

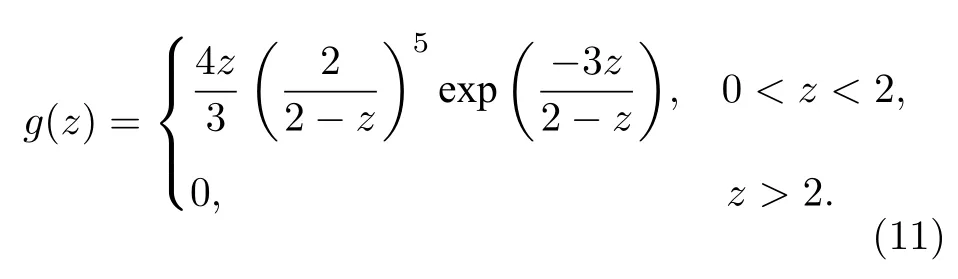
熟化控制方程的完整解則需要通過數值求解方式獲得.

2.3 數值參數設置

一般而言,Ostwald 熟化過程是一種近平衡態的熱力學過程,不考慮水動力學因素.數值計算中初始場需要盡量滿足這些條件.在雙氣泡熟化過程中,首先根據設計條件對單氣泡情況進行計算,測量獲得計算穩定后的氣泡的半徑R1,R2及相應的氣液密度ρ1L,ρ1V和ρ2L,ρ2V.在進行雙氣泡熟化過程初始化時,取初始氣泡半徑為R1,R2,氣、液兩相密度分別為 (ρ1V+ρ2V)/2,(ρ1L+ρ2L)/2 .對雙氣泡初始條件的準確設定,可以減小初始化誤差,從而使有效數據的時間區間延長.對于多氣泡測試,本文參考(11)式對氣泡半徑分布進行設定.此時由于氣泡數目較多,直接根據介質狀態方程結果設定初始氣、液密度.為了避免在氣泡熟化過程中發生融合、破壞理論分析設定的前提條件,氣泡間距須保證足夠大.

本文針對二維空間的多氣泡熟化過程開展LBM 模擬研究,計算域取為矩形,針對不同的氣泡數和氣泡大小,取適當的計算域大小:雙氣泡計算域大小取 1000×500,多氣泡取 3600×3600,氣泡群初始數量約為800.計算域四周邊界取周期邊界.在后處理過程中,本文采用圖像處理技術 (如二值化、邊界提取等),對計算結果圖片進行顆粒幾何特征提取,可以獲得氣泡數、各個氣泡的直徑和位置等信息.

3 模擬結果與討論

本節針對雙氣泡、多氣泡熟化過程開展模擬和分析.前者在反映熟化特征的同時,便于我們對相關細節開展測試,進而對 (模擬的)熟化過程物質輸運細節進行分析;后者對標一般熟化過程,期望探討蒸氣泡群熟化過程的基本規律.

3.1 雙氣泡熟化過程

本部分取τ=1.0 (該參數決定了流體的黏性,本文暫不討論其影響),R1=57,R2=60,氣泡間距d=500,T=0.8Tc為例,給出雙氣泡熟化過程的計算結果.該溫度下,氣、液兩相初始密度分別為ρV=0.01853,ρL=0.3064,氣-液表面張力系數σ=0.0075.前期測算表明,上述結果準確地再現了介質的熱力學狀態[20].

圖1(a)給出了雙氣泡熟化中大小氣泡的發展,顯示了小氣泡消失、大氣泡增長的過程.進一步統計氣泡半徑可以發現,兩個氣泡的大小在發展過程中是振蕩的,這導致了氣相區域總面積 (S)的振蕩 (圖1(b),(c)).原因可能是在進行雙氣泡計算時,密度、速度場初始化仍然不夠精確,引起了不平衡(水動力)壓力波在計算域內來回傳播,從而激勵起氣泡的非物理振蕩.當濾除掉氣相總面積的波動成分后,可以看出氣相總面積是穩定的,且熟化過程最終形成的大氣泡面積十分接近預設氣相面積,這滿足LSW 理論的質量守恒約束條件.該守恒律與水動力學作用占優的空化氣泡發展過程有明顯差別[20].將氣相總面積波動濾除以后,可以獲得更為光順的氣泡半徑演化過程 (見圖1(b)中的紅線).

圖1 雙氣泡熟化過程氣泡演化 (a) 雙氣泡熟化過程相分部演化;(b) 大、小氣泡半徑 (R2,R1)演化,T=0.80Tc,d=500 ;(c) 雙氣泡熟化過程中氣相區總面積 (S)變化.圖(b)和圖(c)中的紅色曲線為濾波結果.對應相變速率系數ks=0.6845Fig.1.Ostwald ripening for two bubbles:(a) Evolution of the two bubbles;(b) relation of R1,R2～t at T=0.80Tc,d=500 ;(c) evolution of the total vapor phase area (S).The red curves are filted results in pannels (a) and (b).Corresponding ks=0.6845 .

另一方面,提取熟化過程中不同時刻,過兩個氣泡中心的軸線上的密度分布演化結果(圖2(a)).可以看出,在熟化過程中氣泡內的密度基本保持不變,而在液相區壓力有明顯波動.因此可以通過Laplace 關系獲得液相壓力分布:大氣泡周圍的液相壓力較高 (pL=pB-σ/R2,pB表示氣泡內的壓力),小氣泡附近的壓力 (pS=pB-σ/R1)較低.圖2(b)給出了小氣泡、大氣泡中心,以及計算域軸線上液相區兩個點 (圖2(a)中以箭頭標記)上的壓力演化時序.圖2(b)中,t ＜2000 時,液相壓力降低,反映了精確密度場的建立過程,同時由于初始階段R1≈R2,因而液相中兩個測點的壓力差距幾乎分辨不出來;隨著氣泡半徑差距拉大,液相壓力梯度逐漸明顯起來.這樣的壓力差異在量級上與Laplace 公式的預測也是符合的:(pL-pS)t=1400≈3×10-4.正是液相中的壓力梯度,驅動了介質往小氣泡一側移動,從而使原來的小氣泡區域逐漸被液相物質所填充.這樣的物質遷移機制替代了經典的Ostwald 熟化理論模型中由離散相濃度梯度驅動的物質遷移機制.從本文結果看,Watanabe 等[14]采用傳統的顆粒擴散假設對蒸氣泡群熟化過程進行描述是有待商榷的.

圖2 雙氣泡熟化過程中密度、壓力分布變化 (a) 雙氣泡中心連線上的密度分布及演化,箭頭標記了壓力測點位置;(b) 圖(a)中測點壓力隨時間的演化過程,空心圈表示數值模擬結果,曲線表示壓力數據的平滑結果.圖標“SB”,“LB”分別表示小氣泡和大氣泡Fig.2.The pressure distribution in bubble and liquid phase during ripening:(a) Pressure distribution at different time,with the arrows marking the detected point in pannel (b);(b) temporal pressure on the four marked points.The open symbols denote the simulated results and the curves the smoothed results.Labels“SB”and“LB”denote large and small bubble,respectively.

進而基于平滑過的氣泡演化數據對熟化過程進行定量分析.在雙氣泡條件下,(4)式和(5)式變得比較簡單:

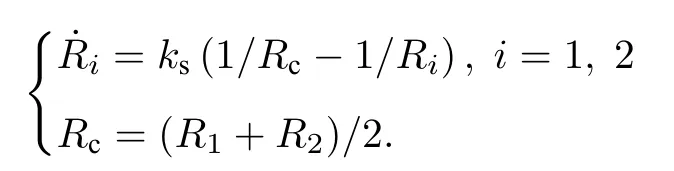
可以直接通過數值方法求解.圖3 給出了大、小氣泡增長速率與相變驅動作用的關系,曲線斜率即為ks.結果表明當前模擬中氣泡增長過程服從LSW理論預測的規律.進一步改變R1,R2和d,發現上述動力學關系仍然得到滿足,且在狀態方程、溫度(T)一定的情況下ks值不變.由此可知,ks可以由介質的狀態方程確定.另外,數據顯示,在熟化過程末期,數據點存在一定程度波動,這可能會影響ks的擬合結果 (對比圖3 插圖).這有可能是由于小氣泡在熟化末期,界面運動速度過快,從而引起了水動力學效應 (與空泡潰滅相似).考慮到圖3 中熟化末期數據點斜率基本與擬合直線斜率相近,以及對于不同算例氣泡半徑演化波動區較難判定,下文仍然采用該統計方法.

圖3 雙氣泡增長速率與相變驅動作用的關系,實心點表示小氣泡,空心點表示大氣泡演化過程.“C1,C2,C3”數據分別對應計算條件(R1/R2/d)=(57/60/500),(57/63/500),(57/60/1000).線性擬合數據點(虛線)得到 ks=0.6845 .圖中箭頭表示熟化過程發展方向Fig.3.The relation of dR/dt～(1/Rc-1/R) .The closed symbols represent small bubbleevolution,and the open ones the large bubble.“C1,C2”and“C3”correspond to the cases (R1/R2/d)=(57/60/500),(57/63/500),(57/60/1000),respectively.A linear fitting shows the slope of ks=0.6845,and the arrows show the directions of the ripening processes for large and small bubbles,respectively.

值得一提的是,Chai 等[29]結合相場方法與LBM 對雙氣泡演化過程進行了模擬,并基于相場方程推導獲得了氣泡演化的解析解.這對本問題具有重要的參考價值,然而也可以看出數學解在實際工程中的應用仍然具有障礙.

3.2 雙氣泡熟化過程的熱力學參數影響

本節圍繞ks與介質狀態方程的關系展開討論.文獻 [19]在探討狀態方程參數對LBM 多相流模擬穩定性影響規律時發現,a會改變氣液界面的厚度;b參數可以影響熱平衡狀態下的氣液密度,但不改變氣液密度比;而R對氣液狀態沒有影響.經典熱力學理論通常只考慮平衡狀態,本節研究從數值角度給出相變速率 (非平衡過程參數)與狀態方程參數之間的依賴關系,同時也可以為面向實際問題的參數設定提供一定的參考.

圖4 給出了不同溫度下的ks值,其中每個ks點綜合了3 種不同初始構型下的雙氣泡演化過程(參見 3.1 節)獲得.結果顯示,盡管對固定 (a,b) 對,ks總體隨溫度T呈降低趨勢 (見(a,b)=(1.0,4.0)數據,實心點),但下降的非線性特征明顯.并且綜合所有數據,ks對溫度T的依賴性并不統一,其同時也決定于其他狀態方程參數.

圖4 ks 對熱力學參數的依賴關系 (a)不同溫度和表面張力下的氣泡增長速率,其中實心點表示 (a=1,b=4) 條件結果,空心點表示表示其他 (a,b) 對結果 (a=1.0,1.05,b=3.75—4.0);(b) W-ks 關系,其中 W 表示介質相變所做的機械功Fig.4.Variation of ks depending on the thermal parameters in ripening process of dual bubble:(a) The T-ks and σ-ksrelations.The close symbols correspond to(a=1,b=4),and the opens for various(a,b)=(1.0-1.05,3.75-4.0).(b) The W-ks relation,where W denotes mechanical work done in phase transition.

經典熟化模型基于兩相界面張力 (σ)解釋了Ostwald 熟化的機理[1,14],其可以進一步引申為化學勢驅動的物質輸運機制.對于單組份兩相等溫過程而言,化學勢可以表達為壓力的函數μ(p)[30].Watanabe 等[14]給出了氣泡界面上液體氣化過程的化學勢變化,相變速率具有包含σ的前置因子.然而他們在隨后的標度律分析中,忽略了前置因子的作用,因而熱力學參數對于相變速率的影響并未深入討論.本研究數值模擬結果(圖4(a))表明,單純的相變速率對表面張力的依賴關系同樣也不能統一地刻畫相變速率的變化.需要補充說明:前期測算表明,對于固定 (a,b) 對,T-σ關系具有很好的線性度,這與實驗觀測和相關理論預測是相符的[31].

從前述溫度越高相變速率越低的現象以及化學勢具有能量的本質出發,可以設想:隨著溫度趨近于臨界溫度、兩相之間密度差的減小,驅動相變所需的機械功 (pdV)也會相應減小.我們基于狀態方程理論解提取了單位質量介質相變的功值,

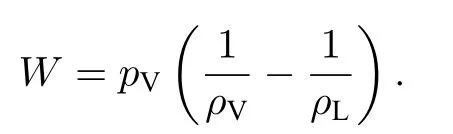
圖5(b)給出了不同熱力學參數條件下ks-W關系,具有較好歸一化特性,并且也與線性變化趨勢較為接近 (其中的偏離可能是由于氣、液密度同時受表面張力影響所致).由此推斷,等溫條件下共存兩相的比內能差可以被看成是驅動相變的根本原因,相變速率與其有正相關關系.

3.3 多氣泡熟化過程

基于前面兩節的討論,進而對多氣泡熟化過程開展分析.如前文所述,本節對密度場做簡單初始化,重點參考(11)式對氣泡初始半徑分布進行設定:在半徑 0—32 范圍內取32 個分度,每個分度中按照半徑分布函數 (11)式分配氣泡數量 (總數800),這些氣泡隨機在計算域內分布.為了與理論預測結果相對比,計算域需要設得足夠大,以保證氣泡群在熟化過程中不發生碰撞/合并.典型的多氣泡熟化過程如圖5(a)所示.在氣泡群熟化過程中,氣泡數量逐漸減少(小氣泡消失)并伴隨著留存氣泡尺度的增加,相應氣泡的臨界 (平均)半徑亦會增大.

圖5 氣泡群熟化過程計算結果 (a) T=0.80Tc 氣泡群熟化過程;(b) 氣相面積演化 (T=0.80Tc)和不同溫度條件下氣泡群臨界半徑增長趨勢,ψ 全場氣相面積占比;(c) 不同溫度條件下計算域內氣泡數量演化過程.圖中斜線顯示了 N～t-1 標度律Fig.5.The simulated ripening process for vapor bubble cluster:(a) Bubble distribution in the ripening process as T=0.8Tc ;(b) vapor area ratio (ψ) evolution (T=0.8Tc) and relations for different temperatures;(c) bubble number evolutions for different temperatures.The dashed line indicates the N～t-1 scaling.

圖5(b)給出了相應氣泡群Rc和計算域內氣相所占面積的比例 (ψ)隨時間的變化,可見Shan-Chen-LBM 多相流模型在相變速率主控的熟化模擬中可以很好地保持氣相面積的守恒性 ((7)式),同時由于多泡的平均效應,此條件下壓力波造成的氣泡總面積波動也被抑制了.氣泡總面積的守恒保證了氣泡群臨界半徑演化 (數值結果)的t1/2標度律關系 ((8)式),以及氣泡數量的t-1標度律((9))式、圖5(c)).圖5(b)中,各組～t的數據點對應的斜率與雙氣泡條件下的氣泡增長斜率相匹配,這說明多泡條件下的氣泡增長與雙泡時的機理是一致的.針對當前計算參數,本文同時也調節了計算域面積、氣泡間距、氣泡排布等幾何條件,所獲標度律結果與展示結果一致 (誤差小于5%).F

如前文所述,在LSW 理論分析基于 的時間相似性 ((11)式),圖6(a)給出了采用有限差分方法對聯立方程組 (4)式—(6)式進行數值求解所獲得的結果.其中,空間微分項?(R˙F)/?R采用迎風格式進行離散,時間推進采用顯示格式[32].方程中ks值采用了圖5(b)中測量獲得的數據點斜率值:

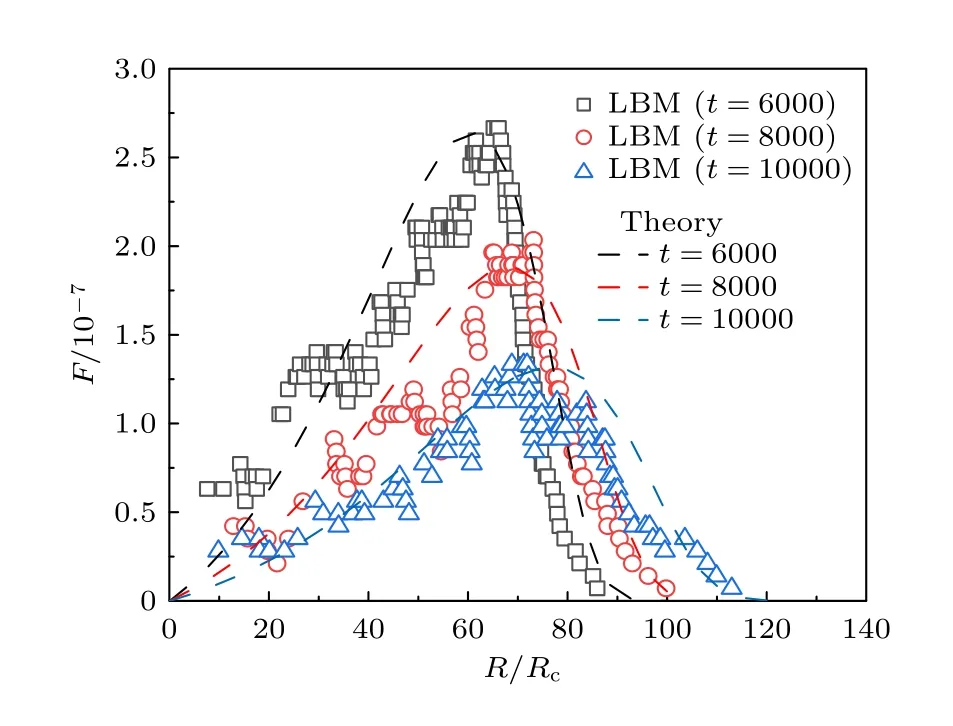
圖6 氣泡半徑分布函數演化結果Fig.6.The evolution of F -R relation in ripening process.

進一步仔細對比理論預測曲線與計算結果可以發現:計算結果在小尺度區域存在F上翹的趨勢,并且在氣泡極小區域存在數據點缺失的現象.這主要是由于小氣泡收縮的最后階段表面張力作用極大 (∝σ/R),導致了水動力學意義上的“空泡潰滅”現象,使小氣泡過快消失.綜合整個R數據段的F分布結果可以知道,小氣泡的水動力學潰滅作用對于大半徑區氣泡影響較小,這可能是空泡潰滅過程帶來的壓力波動在液相中傳播.可以想象當壓力波波長大于某個氣泡的尺度時,會明顯影響相變過程;對于氣泡而言這樣的影響會比較小.事實上,在計算結果中確實發現,在熟化過程中,一些小氣泡在收縮過程中存在抖動現象.氣泡潰滅的水動力學效應特征是蒸氣泡群熟化與顆粒或者乳狀液熟化過程的不同之處.

4 結論

本文采用格子Boltzmann 方法對二維條件下的蒸氣泡群Ostwald 熟化現象開展數值研究.Shan-Chen 多相流模型以及Carnahan-Starling 狀態方程用以捕捉真實介質的相變和相分離過程.本文針對二維條件重新推導了基于Lifshitz-Slyozov-Wagner 理論體系的氣泡系統特征參數的標度律關系,并針對相變速率主控的雙氣泡和多氣泡系統熟化過程開展了模擬和分析.研究結果如下.

理論分析和數值模擬同時證實,二維氣泡群的反應速率主控的熟化過程中,氣泡半徑增長率受氣泡間化學勢差異驅動,服從=ks(1/Rc-1/R) 規律,由此進一步導致氣泡群統計參數服從Rc～t1/2,N～t-1標度律.該結果證實了格子Boltzmann方法對復雜多相流-相變過程捕捉的適用性,相對于傳統流體力學數值方法,具有先天的優越性.

對于雙氣泡系統氣、液兩相密度場演化的仔細觀測表明,在熟化過程中液相密度分布具有時變波動特征,并且大氣泡附近的壓力高于小氣泡周圍的壓力.這樣的壓力分布一方面折射了Laplace 壓力定律的內涵,同時也顯示液相內的物質輸運由該壓力不均勻性驅動,而非傳統熟化理論中所提的濃度梯度驅動的輸運機理.

區別于經典熟化理論中忽略了界面移動的慣性效應,本文結果顯示小氣泡收縮的最后階段,水動力學意義的空化氣泡“潰滅”作用會加速小氣泡的消失,從而造成氣泡群半徑分布函數的小半徑分支偏離理論預測值,并且在細小氣泡區造成函數曲線的截斷現象.

本研究基于格子Boltzmann 方法重點研究了相變速率主控的蒸氣泡群的熟化過程.相對于基于熱力學平衡態假設發展出的理論、數值方法而言,本方法具有更明確分子動力學基礎,可以作為微觀粒子運動與宏觀物理現象的橋梁.本研究為進一步發展格子Boltzmann 數值方法、揭示相變機理,乃至解決實際的工程問題奠定了堅實基礎.在本研究基礎上,可以進一步開展受限空間的顆粒群熟化現象、溫度影響、流動影響,以及擴散主控熟化現象等方面的研究.

感謝西北工業大學材料學院劉峰教授、中國科學技術大學近代力學系黃海波教授、南方科技大學航空航天工程系單肖文教授給予本工作的關注和討論.

附錄 A

針對連續性方程

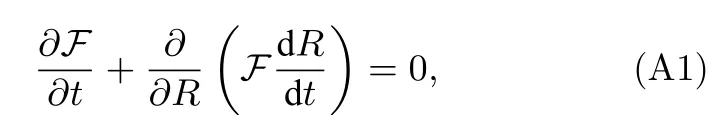
基于顆粒熟化過程中F的相似性,引入標度率關系:

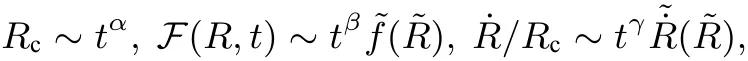
可以得到β=-3α.同時也可以獲得體系中顆粒總數滿足

另外,將前述標度律關系代回到連續性方程 (A1),配平t的指數,可以得到γ=-1,因此只剩α未知.在反應主控熟化過程中,乳狀液體系中小液滴的長大/縮小的速率已經由前人討論過.針對蒸氣泡問題,Watanabe等[14]根據Gibbs-Thomson 公式,對單位面積相變質量通量進行了估算:

其中,ρR表示氣泡內蒸氣的密度,ρ∞表示平直液面條件下的氣體平衡密度,表示半徑為R的氣泡界面上的平衡氣體密度,λ為毛細尺度,它由表面張力、溫度、氣體分子摩爾體積決定.由此可得

即α=1/2 .更進一步Rc～t1/2,N～t-1(注意,二維情況下的標度律與三維有差別).