基于ADAMS與MATLAB的平面六桿機構運動分析

摘? 要：運用解析法對平面六桿機構進行運動規律分析，通過數學模型建立六桿機構的運動方程，進行位移、速度和加速度的分析。利用MATLAB建立運動分析程序并繪制出運動曲線圖。利用ADAMS建立六桿機構虛擬樣機進行運動仿真并獲得運動參數曲線圖，通過分析兩者輸出的運動參數圖像，發現兩者的仿真結果具有一致性。并且，使用ADAMS仿真對機構進行運動分析可以提高分析的效率，能精確實現對平面六桿機構的運動學精確分析，這對機械系統的運動方案設計結構的優化具有重要的意義。

關鍵詞：平面六桿機構;運動分析;MATLAB仿真;ADAMS仿真

中國分類號：TP391.9? ? ? ?文獻標識碼：A文章編號：2096-4706（2022）01-0100-06

Abstract： Analyze the motion rule of plane six-bar mechanism by analytic method， and establish the equation of motion of the six-bar mechanism through the mathematical model， then analyze the displacement， velocity and acceleration. MATLAB is used to establish action analysis procedure and draw the motion curve graphs. ADAMS is used to establish a six- bar mechanism virtual prototype for motion simulation and obtain the motion parameter curve graphs. By analyzing the two deferent motion parameter images， it is found that two deferent results are consistent. Moreover， using ADAMS simulation to analyze the motion of mechanism can improve the efficiency of analysis and realize the accurate kinematic analysis of the plane six-bar mechanism， which is of great significance to the optimization of the scheme design structure of the mechanical system.

Keywords： plane six-bar mechanism; motion analysis; MATLAB simulation; ADAMS simulation

0? 引? 言

機構運動分析是在給定機構尺度及原動件運動規律時分析機構從動件、各運動副運動規律[1] ，從而分析機構運動性能。無論是對于了解已經存在的機械的運動性能，還是對于創造設計新的機械，機構的運動分析都是十分必要的。可以通過對機構進行速度上的分析，再根據設計要求，來判斷從動件的運動規律是否合適。而通過軌跡和位移的分析，可以直觀地觀察到構件的運動空間軌跡，這能夠確定從動件的運動行程，判斷某一構件的是否能按設計要求實現預定軌跡和到達預定位置等。也可以觀察到機構運動時，是否有構件軌跡上的相互干涉。例如牛頭刨床[2，3]在設計時，要求既能提高加工質量，節省動力，同時要把延長刀具壽命和提高效率考慮在內，因此就要求該機器具有急回特性，空載回程速度應該高于工作的進程速度，而且進程速度應該相對穩定，接近與等速。因此，為了判斷設計的機器是否滿足要求，就有必要對其進行運動分析。

MATLAB是通用數學和工程仿真軟件，被譽為巨人肩上的工具，其廣泛應用在數理統計、機械設計、自動控制和流體力學等工程領域中，是一款功能強大的工程計算軟件，包含眾多工具箱，通過強大的圖形功能輸出數值計算的結果，進行圖形顯示，高效地求解出復雜的工程問題 [4-7] 。ADAMS是虛擬樣機分析軟件，是研究機械動力學運動仿真的有效工具，其仿真結果可用于預測機械系統的性能、運動范圍等，這對機械系統的設計和優化都具有重要的意義[8-11]。

本文將利用ADAMS與MATLAB對牛頭刨床的六桿機構進行運動分析。首先利用ADAMS中的模塊建立構件，在構件之間添加運動副，在運動副上添加驅動，建立出牛頭刨床六桿機構的模型，并對其進行運動仿真。通過建立六桿機構的位置數學模型，用解析法建立六桿機構的運動方程，進行位移、軌跡、速度和加速度的分析。然后利用MATLAB建立六桿機構的運動分析程序，運行得到運算分析結果，繪制出從動件、運動副的位移、速度和加速度以及角速度、角加速度等的運動曲線圖為平面六桿機構的運動學設計提供參考。

1? 建立六桿機構模型

本文以牛頭刨床平面六桿機構為例，首先對其模型進行簡化，可以畫出其運動簡圖，如圖1所示，其中曲柄2是原動件，逆時針轉動，ω2=172 r/min，且LBE=L2=100 mm;CD是桿件3，是與滑塊C相連的導桿，LCD=L3=250 mm;AD是桿件4，是由曲柄2直接帶動的擺桿，LAD=L4=400 mm;另外已知的有主動件2到機架的距離LAB=L1=200 mm，滑塊C到機架的距離LAF=L5=440 mm。另外，設滑塊C到Y軸的位移為M2，滑塊E到A點的距離為M1。

1.1? 自由度的計算C942CCEE-3113-4099-BAFE-59898B4F5982

自由度的計算公式為F=3n-（2Pl+Ph），其中n=5為自由構件數，Pl=7為低副數，高副數Ph=0。由此我們可以計算出該機構的自由度為F=3n-（2Pl+Ph）=1。可知，當主動件2的運動參數確定的情況下，該機構有確定的運動輸出。可以通過計算得出桿件3、4的角速度，角加速度，以及滑塊C的位移、速度和加速度等。

1.2? 位移分析

對平面機構進行運動分析的方法主要有解析法和圖解法。圖解法具有簡單和形象直觀的優點。但也因此具有精度不高的缺點，特別是當要對機構的一系列位置進行軌跡分析時，就需要反復作圖，其工作量是相當大的，也相當的復雜。相對來說，解析法就具有精度高的優點，解析法是通過列方程把機構中已知的運動參數，尺寸參數和位置的運動變量之間的關系表達出來，然后對運動方程進行求解。其缺點是不像圖解法那樣形象直觀，計算公式比較復雜，計算量也比較大，但是由于計算機的普及，計算量的問題得到了解決，因此，現在應用較為廣泛的是解析法。本文將利用解析法對該六桿機構進行運動分析，其中包括位移、速度和加速度的分析，也包括角速度和角加速度的分析。除二級桿組可以將位置表達為顯函數形式，對于復雜機構該位置方程通常是非線性方程組，所以需利用數值方法求解位置方程。因此，連桿機構的運動分析重點在位置求解。至于速度、加速度方程式則全為線性方程，因而求解較為簡單。

對于該六桿機構，由圖1我們可以寫出如下兩個矢量方程：

將兩個方程對坐標軸X軸和Y軸投影，我們便可以得到投影方程，如下所示：

聯立公式（1）（2）（3）（4），由各個桿件的長度和主動件2的角度θ2都是已知，因此可以求解出滑塊C到Y軸的位移量M2，滑塊E到A點的距離M1，以及桿件3和桿件4的角度θ3和θ1如下：

1.3? 速度分析

速度方程可以由位移方程對時間求導得到，將式（1）（2）（3）（4）對時間求導，并整理得到速度方程如下：

在位移求解的過程中我們已經算得M2、M1、θ3和θ1大小，將速度方程進行整理我們可以得出構件3、4的角速度和滑塊C的速度如下：

1.4? ?加速分析

由速度方程再對時間求導，便可以得到相應的加速度方程，將式（5）（6）（7）（8）對時間求導得到如下的加速度方程：

整理之后，由先前所求解得的各個參數，可以解得滑塊C的加速度和構件3、4的角加速度如下：

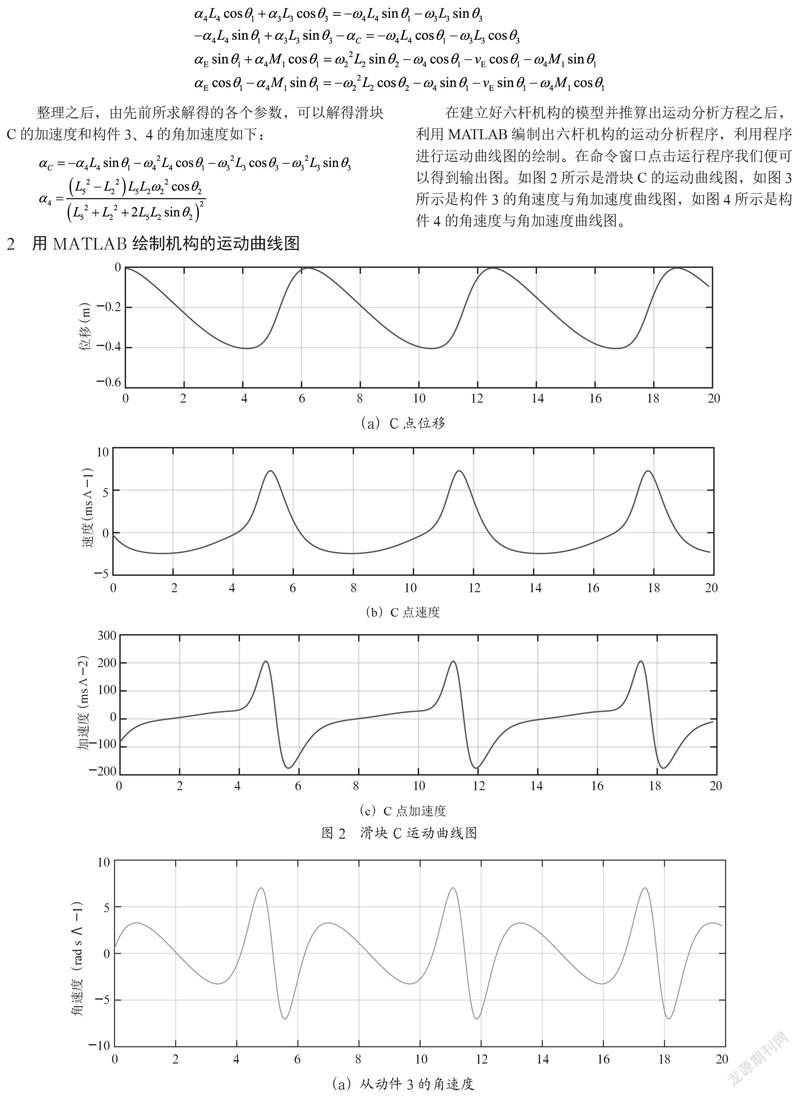
2? 用MATLAB繪制機構的運動曲線圖

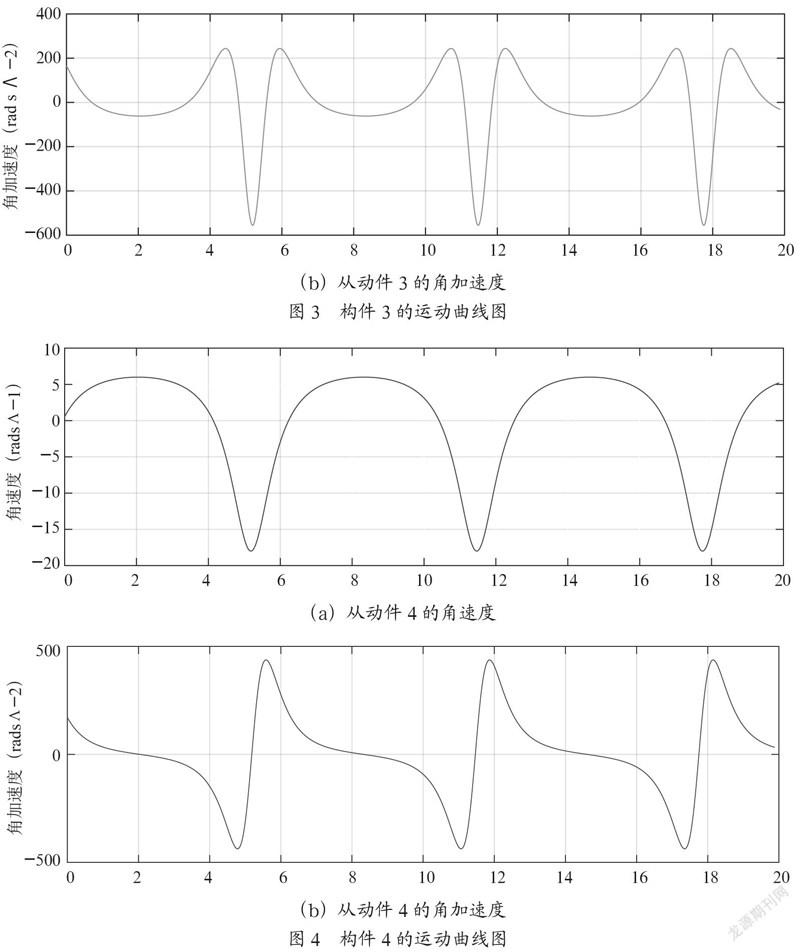
在建立好六桿機構的模型并推算出運動分析方程之后，利用MATLAB編制出六桿機構的運動分析程序，利用程序進行運動曲線圖的繪制。在命令窗口點擊運行程序我們便可以得到輸出圖。如圖2所示是滑塊C的運動曲線圖，如圖3所示是構件3的角速度與角加速度曲線圖，如圖4所示是構件4的角速度與角加速度曲線圖。

3? 運用ADAMS對機構進行建模與仿真

3.1? 建立機構的ADAMS模型

在Adams軟件中，點擊Link模塊，在框圖中輸入構件的參數，可以完成構件2的建立，同理可以建立導桿3、擺桿4，以及滑塊C和滑塊E等構件。

完成構件的建立之后，進行添加構件之間的連接。在Adams軟件中點擊連接模塊，分別在曲柄2與地面、曲柄2與滑塊E、搖桿4與地面、搖桿4與搖桿3、搖桿3與滑塊C之間添加轉動副;在搖桿4與滑塊E、地面與滑塊C之間添加移動副。

完成了機構所需的運動副的添加之后，再添加驅動。在曲柄2上的轉動副上添加上旋轉驅動，設置驅動的函數為速度為57 d*time，點擊完成。此時六桿機構的建模便完成了，完整的模型如圖5所示。

3.2? 運動仿真分析

在保存模型之后，點擊仿真模塊，進行仿真設置，將仿真時間設置為20秒，步數設置為640，如圖6所示。仿真開始之后，將可以在界面中直接觀察到模型的運動動畫，待仿真結束后，將仿真結束進行繪圖，便可以得到整個模型中各個構件的運動分析曲線圖，我們將構件3、4的角速度、角加速度和滑塊C的位移、速度和加速度的圖像輸出，如圖7、圖8所示。

通過對位移圖的分析，我們可將在時間0 s～4 s的區間內機構的運動稱為進程，在4 s～6 s之間機構的運動稱為回程。而且由圖4可知，當t=0 s 時達到最小值，當t=4 s 時達到最大值，當t 在0 s～4 s的區間內，位移與時間基本呈線性關系，說明速度變化平穩，這一點在速度曲線圖中也可以看出來。而當t=6 s時，滑塊C 又回到了初始位置點，并且在t=4 s～6s 區間內，速度曲線變化很快，在1 s內快速從0 增長到極值點，又在1 s內快速變為0，而且速度的峰值接近進程區間時的3 倍。在加速度曲線圖中也可以看出在進程區間內加速度的變化趨于平穩，而在回程區間內加速度在2 s 的時間內極速變化了三次。這正是該機構的急回特性，很明顯可以得出回程時間是進程的1/2，進而計算得行程速度變化系數K=v進/v回=2。因為該機構進程時是在對外做功的，而回程是空載的，因此機構需要得到更長的進程時間，而回程則需要盡快地完成，通過運動分析我們發現該機構符合這樣的設計要求。另外，通過與MATLAB 圖像輸出進行對比我們發現，兩者的結果具有一致性。這說明兩者的運動分析都是正確的。

構件4是直接與主動件連接的桿件，如圖9所示是構件4的角速度曲線圖，如圖10所示是構件4的角加速度曲線圖。從圖中可以看出，在進程的時間區間0 s～4 s內，角速度和角加速度的變化都較為平穩，且極值都相對較小;而在回程的時間區間4 s～6 s內，角速度和角加速度都有突變的發生，變化很大，而且極值相對較大。這樣的變化正是因為該機構的急回特性，在構件4的運動中也得到了體現。C942CCEE-3113-4099-BAFE-59898B4F5982

構件3是直滑塊C連接的桿件，如圖11所示是構件3的角速度曲線圖，如圖12所示是構件3的角加速度曲線圖。在分析這兩個圖時我們會發現無論是角速度曲線角加速度曲線，都比構件4更加復雜。但仔細分析后不難發現該機構的急回特性仍然在構件3的運動中體現了出來。在進程的時間區間0 s～4 s內，角速度和角加速度的變化雖然復雜，有較小的拐角，但都較為平穩，且極值都相對較小;而在回程的時間區間4 s～6 s內，角速度和角加速度都有突變的發生，變化很大，而且極值相對較大。

4? 結? 論

通過將ADAMS軟件仿真結果與MATLAB圖像輸出進行對比我們發現，兩者的結果具有一致性。這就說明，兩者的運動分析結果都是正確的。兩者都實現了六桿機構的運動分析，并且相互驗證了正確性和有效性，既證明了利用ADAMS仿真進行運動分析的正確性，也證明了數學模型的建立和利用MATLAB編程求解運動規律的正確性。與此同時，我們會發現，運用ADAMS實現機構的運動仿真比用MATLAB編程繪圖更加方便，而且ADAMS仿真過程中可以輸出機構運動動畫，可以更加直觀地觀察到機構運動過程。相對用復雜的解析法推算運動方程，然后運用MATLAB來編程繪制出運動曲線圖，運用仿真的方法省去了較為煩瑣的模型建立，矢量方程的計算等步驟，仿真結果不易出錯直觀性強，相對計算量較小，更具有一定的工程實際意義。對于復雜的機械系統來說，有時候矢量方程的建立特別煩瑣，編程也就特別的復雜。此時，運用ADAMS進行運動分析，就會更加高效，能為工程師節省時間，具有更強的工程實際意義，同時這對機械系統的設計和優化都具有特別重要的理論意義。

參考文獻：

[1] 于靖軍.機械原理 [M].北京：機械工業出版社，2013.

[2] 徐金明.MATLAB實用教程 [M].北京：清華大學出版社，2005.

[3] 陳懷琛.MATLAB及其在理工課程中的應用指南 [M].西安：西安電子科技大學出版社，2007.

[4] 管西巧，趙慶志，高躍武，等.基于Solidworks和ADAMS的牛頭刨床導桿機構仿真分析 [J].煤礦機械，2014，35（10）：273-275.

[5] 王延龍，文學洙.牛頭刨床六桿機構的運動分析和優化方法 [J].機械工程師，2016（2）：98-99.

[6] 季佳俊.基于MATLAB的牛頭刨床機構運動分析 [J].時代農機，2020，47（1）：112-114.

[7] 張森，張正亮.MATLAB仿真技術與實例應用教程 [M].北京：機械工業出版社，2004.

[8] 楊春輝.基于MATLAB的平面六桿機構運動分析 [J].重慶科技學院學報（自然科學版），2008（1）：55-57.

[9] 趙玉成，頓文濤，李勉，等.基于Pro/E的牛頭刨床六桿機構的動態仿真分析 [J].河南農業大學學報，2014，48（1）：66-70.

[10] 劉文龍，蘇丹，劉明濤.基于Matlab與C語言聯合對牛頭刨床機構的優化研究 [J].河南工程學院學報（自然科學版），2015，27（3）：45-51.

[11] 管鋒，周傳喜，喻久港.基于VB的牛頭刨床六桿機構參數化設計及運動分析 [J].長江大學學報（自然科學版），2012，9（12）：149-151+6.

作者簡介：詹春暉（1995—），男，漢族，江西婺源人，碩士研究生在讀，研究方向：計算機輔助工程。C942CCEE-3113-4099-BAFE-59898B4F5982