基于拉普拉斯正則化的藥物副作用頻率預測

王 林，李冰純，徐顯崳

(天津科技大學人工智能學院，天津 300457)

藥物風險-效益評價是對患者用藥后得到的治療效益與風險之間的評價.在這項評價中，藥物副作用頻率的估計至關重要[1].目前，計算頻率的標準方法是隨機對照實驗，通過對不同分組實施不同的干預措施，得到不同的結果[2].這種方法容易受到時間、樣本量和熟練度的限制，使藥物的一些副作用在臨床試驗中沒有發現，而是在上市多年后被發現[3].因此在醫療衛生領域中，藥物的副作用仍然是引起其他疾病和死亡的主要原因[4].現有的一些預測藥物副作用的計算方法[5-7]大多數只能預測副作用存在與否，不能預測副作用的頻率，在一定程度上限制了這些方法在藥物風險-效益評價中的應用.

Galeano等[8]提出了利用非負矩陣分解模型(nonnegative matrix factorization，NMF)預測藥物的副作用頻率，但是該方法對藥物副作用關聯和頻率預測的準確率仍有待提高.在此基礎上，本文提出了一種基于拉普拉斯正則化的藥物副作用頻率預測模 型DSLR(drug-side effect frequency prediction with Laplace regularization)，在非負矩陣分解模型中引入拉普拉斯正則化項，以及控制未知副作用標簽及其預測值間隔的超參數.實驗結果和數據分析表明，DSLR模型不僅能更準確地識別藥物的副作用關聯，而且能更精確地進行藥物副作用頻率的預測.

1 數據獲取

利用Galeano等[8]和Zhao等[9]使用的基準數據集驗證藥物副作用頻率預測方法的有效性.該數據集包括750種藥物和994種副作用，以及來自SIDER數據庫[10]的37071個已知頻率項.藥物副作用依據干預隊列，臨床試驗頻率被映射成5個頻率(f )區間，即f＜0.01%、0.01%≤f＜0.1%、0.1%≤f＜1%、1%≤f≤10%和f＞10%分別定義為罕見、少見、不經常、頻繁和非常頻繁，并分別用頻率值1、2、3、4、5表示.在37071個已知頻率項中，罕見、少見、不經常、頻繁和非常頻繁的占比分別為3.21%、11.29%、26.92%、47.46%和11.12%.用評級矩陣M表示藥物和副作用之間的頻率，其中矩陣的行和列分別表示藥物和副作用，矩陣中的非0值表示特定藥物-副作用對的已知頻率，0表示未知副作用.評級矩陣M極其稀疏，非零元素僅占4.97%.

2 計算方法

2.2 藥物相似性和副作用相似性的構建

2.2 基于拉普拉斯正則化的優化模型

2.3 求解算法

采用乘性更新算法求解模型(4).具體來說，隨機初始化W和H，并分別用其Frobenius范數歸一化，進而W和H的更新公式為

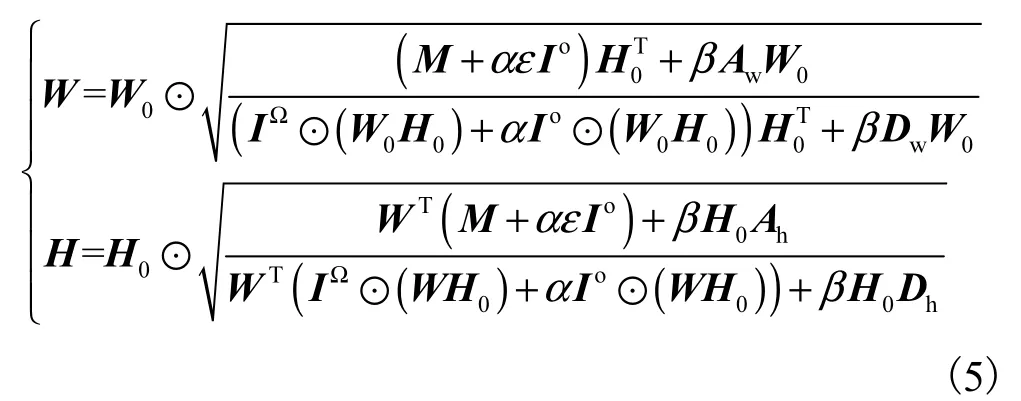
其中：W0和H0為更新前的矩陣，W和H為更新后的矩陣.基于更新公式(5)，模型(4)的目標函數是單調下降的，從而可以保證算法的收斂性.設置最大迭代次數為1000，并且當前后兩次迭代目標函數的下降值小于設定閾值時，停止迭代.

算法執行前，首先運用M/5將評級矩陣M歸一化，然后采用上述乘性更新算法得到W和H，進而令P＝WH，最后通過P×5得到最終的預測矩陣.

2.4 收斂性分析

根據約束最優化理論[11]，當目標函數收斂時，最優解滿足的Karush-Kuhn-Tucker(KKT)互補條件為

當W＝W*且H＝H*使模型(4)取得局部極小值時，必須滿足式(6)中的KKT互補條件，其中W*和H*表示局部最優解.將式(7)代入式(6)，得

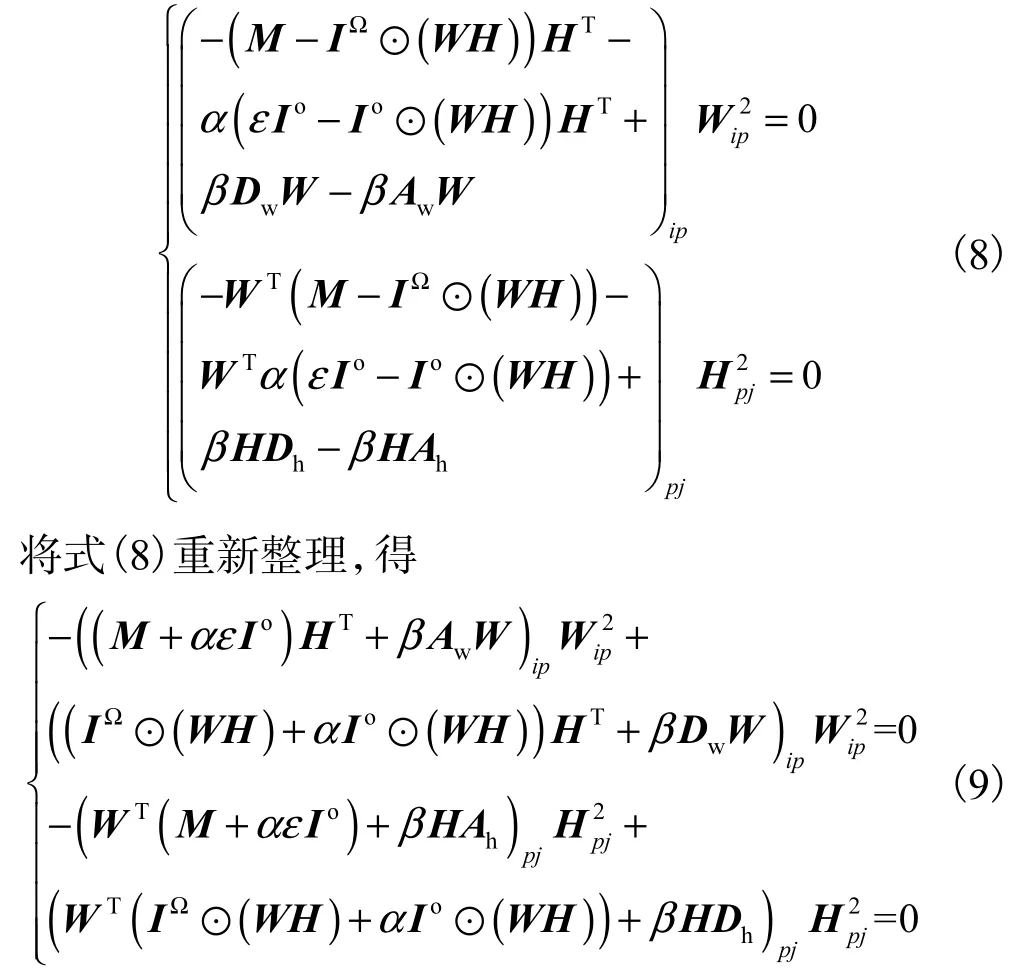
結合式(9)不難看出，W和H的更新公式(5)滿足KKT互補條件，從而基于式(5)則模型(4)收斂到局部最小值.

2.5 預測性能的度量

預測模型的準確性從兩個方面衡量，即識別藥物副作用關聯的性能和頻率預測的性能.對于二分類問題，可以將實例(藥物-副作用對)分為正例(有關聯)或負例(未知關聯).進行預測時，會出現以下4種情況：True Positive(TP)，實例是正例并被預測為正例；False Positive(FP)，實例是負例并被預測為正例；False Negative(FN)，實例是正例并被預測為負例；True Negative(TN)，實例是負例并被預測為負例.

準確率(Accuracy)、精確率(Precision)、召回率(Recall)的計算式為

此外兩個常用的指標，即Precision-Recall(PR)曲線下面積(area under the precision-recall curve，AUPR)以及接受者操作特征曲線(receiver operating characteristic curve，ROC)下面積(area under curve，AUC)也用來評價關聯性能.

對于每個指標，首先計算測試集上每種藥物的指標值.對于每種給定的藥物，其在測試集中具有已知頻率的副作用和其在評級矩陣M中的未知副作用分別被視為正例和負例，然后將所有藥物的平均指標值作為結果.

關于頻率預測，使用Spearman相關系數(Spearman’s correlation coefficient，SCC)和均方根誤差(root mean square error，RMSE)作為評價指標，SCC和RMSE的計算式為

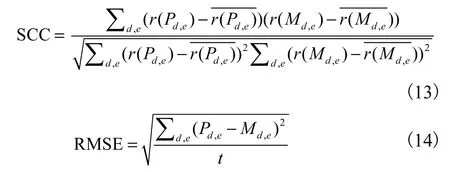
其中：d和e分別表示藥物和副作用的遍歷，Pd,e和Md,e分別表示藥物-副作用對的預測頻率和已知頻率，r () 表示等級轉換，t表示已知頻率的藥物-副作用對的總數.

3 計算結果與討論

3.1 化學結構相似的藥物有相似的副作用頻率

使用開源化學信息Python軟件包RDKit，基于拓撲指紋和Tanimoto相似度計算任意兩個藥物之間的化學結構相似性.對于280875個藥物對，其化學結構相似性的中位數為0.24，將相似性≤0.24的藥物對定義為化學結構低相似度對，將相似性＞0.24的藥物對定義為化學結構高相似度對.

對于280875個藥物對，計算其副作用頻率相似度，即對于任意兩個藥物，基于其副作用頻率譜(評級矩陣M中的兩行)，利用余弦相似度進行計算.藥物對關于副作用頻率余弦相似度的箱線圖如圖1所示.圖1給出了化學結構低相似度對和高相似度對的副作用頻率相似度分布的箱線圖，相對于化學結構低相似度對，化學結構高相似度對具有更大的副作用頻率相似度(單邊Wilcoxon秩和檢驗P＝5.85× 10-59).

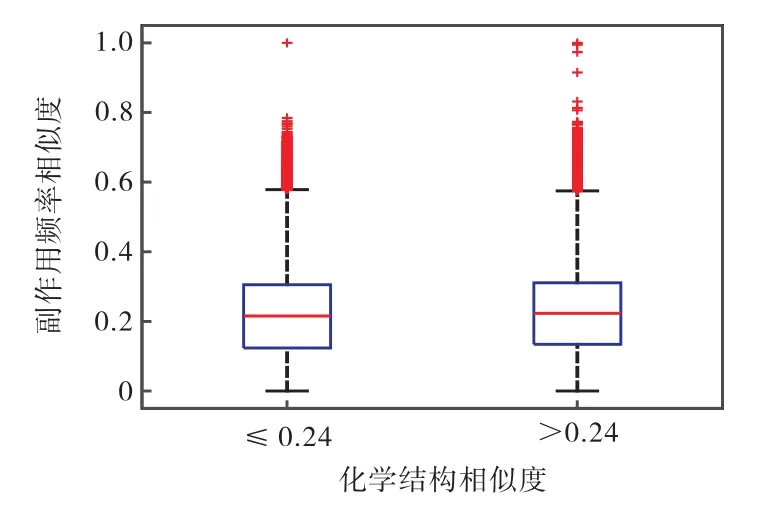
圖1 藥物對關于副作用頻率余弦相似度的箱線圖 Fig.1 Box plots of drug pairs with respect to the cosine similarity between their side effect frequency profiles

3.2 10折交叉驗證

在數據集中，所有已知藥物-副作用對的頻率(共計37071個)被隨機均勻地分成10折.數據集的其中一折設置為測試集，其余9折則作為訓練集，并將每一折測試集的平均指標值作為最終結果.選擇現有的副作用頻率預測模型NMF[8]和MGPred(prediction using a graph attention network.to integrate multiview data)[9]作為對比，驗證本文模型DSLR的有效性.同時，考慮建模副作用頻率預測問題為推薦系統，采用基于圖神經網絡的模型(inductive graphbased matrix completion，IGMC)[12]求解.基于10折交叉驗證的比較結果見表1.由表1可知：DSLR模型的AUC、AUPR明顯優于其他3個模型，這表明DSLR模型可以對藥物副作用關聯進行更好地預測；對于評價頻率預測性能的指標，DSLR模型的SCC和RMSE明顯優于NMF模型，但遜于MGPred模型和IGMC模型.MGPred和IGMC這兩個模型的AUC較低，表明其不能準確地預測藥物-副作用關聯，因此雖然其SCC和RMSE更優，但在實際使用中容易引入假陽性，即未知副作用大多數被預測為有藥物-副作用關聯.

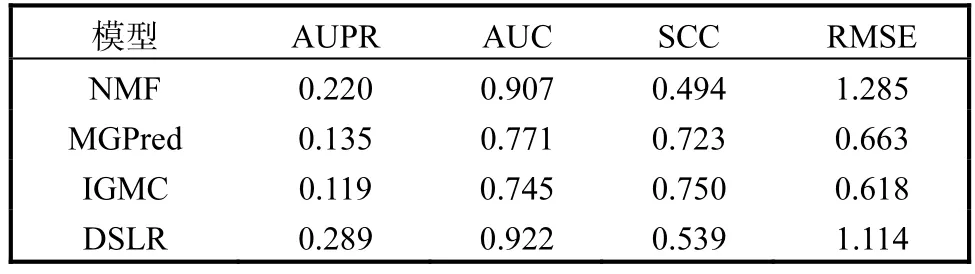
表1 基于10折交叉驗證的比較結果 Tab.1 Comparison results based on 10-fold cross validation

使用DSLR模型對單個藥物氟伏沙明進行研究.對于10折交叉驗證中的1折，測試集中氟伏沙明的已知副作用共35個(正例)，未知副作用共694個(負例).選取與正例等量的負例，計算得出Accuracy＝0.614，Precision＝0.565，Recall＝1.0.該藥物對于729個副作用預測結果的ROC曲線 (AUC＝0.948)和PR曲線(AUPR＝0.559)見圖2.

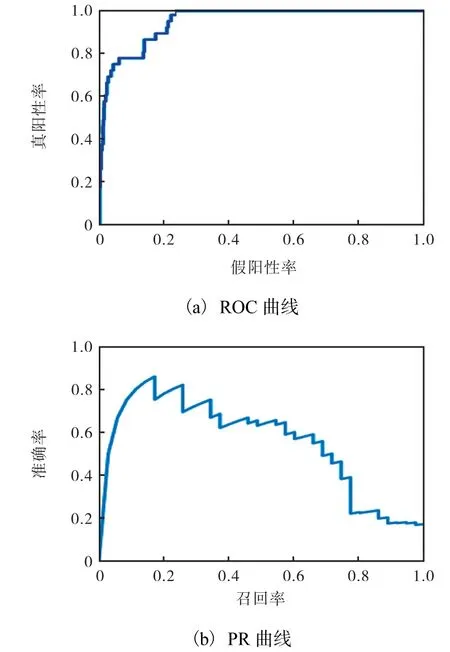
圖2 藥物氟伏沙明副作用預測的ROC曲線和PR曲線 Fig.2 ROC curveand PR curve for the prediction of the side effects of the drug fluvoxamine

為了進行頻率類別預測，使用10折交叉驗證期間從測試集得到的預測值，收集了所有已知副作用的頻率類別及其對應的預測值.對于未知副作用，基于10折交叉驗證中的1折，得到未知副作用的預測值.對于未知副作用及已知副作用的每個頻率類別，采用核密度估計方法得到其預測值的概率密度函數(probability density function，PDF).每一頻率類別預測值的概率密度函數如圖3所示，其中頻率0～5分別對應副作用頻率類別為未知副作用、罕見、少見、不經常、頻繁和非常頻繁.

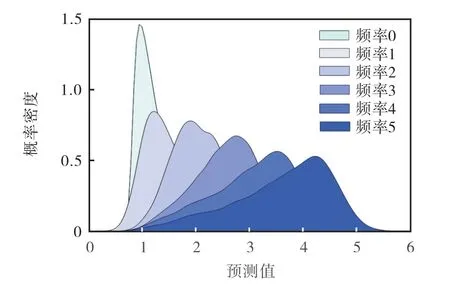
圖3 每一頻率類別預測值的概率密度函數 Fig.3 PDF of predicted values for each frequency category

根據概率密度函數和最大似然法確定分類決策的邊界，得到相鄰頻率的邊界閾值分別為1.15、1.65、2.35、3.05和3.85(圖3).對于每一個真實頻率類別中的所有副作用，可以得到其預測頻率類別.每一頻率類別的準確率見表2.表2給出了預測為各個類別的副作用所占的百分比，對于頻繁(頻率＝4)副作用(占總數的47.46%)中的41.89%被正確預測， 79.67%被預測為不經常(頻率＝3)、頻繁或非常頻繁(頻率＝5).

進一步定義精確類和鄰居類兩個概念.精確類是被預測為自身真實頻率的類別，如真實頻率為1的副作用被預測為頻率類別1.鄰居類是指被預測為自身和其鄰居真實頻率的類別，如真實頻率為1的副作用被預測為頻率類別1和2，真實頻率為2的副作用被預測為頻率類別1、2和3.

本研究對單個藥物鹽酸羅匹尼羅進行了分析，該藥物共有396個副作用，頻率為1、2、3、4和5的副作用個數分別為0、17、167、209和3.該藥物頻率為2、3、4和5的精確類準確率分別為11.76%、28.74%、30.62%和33.33%，鄰居類準確率分別為41.17%、68.26%、84.21%和66.66%.

3.3 消融實驗

在引入拉普拉斯正則化項以及控制未知副作用標簽和其預測值間隔的超參數ε后，驗證DSLR模型在預測藥物副作用頻率方面的優越性(表3).對于給定的基準數據集，引入拉普拉斯正則化項對模型預測藥物-副作用關聯的性能有明顯提升；引入超參數ε，在AUC相對穩健的情況下，RMSE顯著降低，表明其能更精確地進行頻率預測.因此，當拉普拉斯正則化項的權重參數β＝0.01、間隔ε＝0.195時，AUC＝0.922，RMSE＝1.114，DSLR模型的預測性能最好.

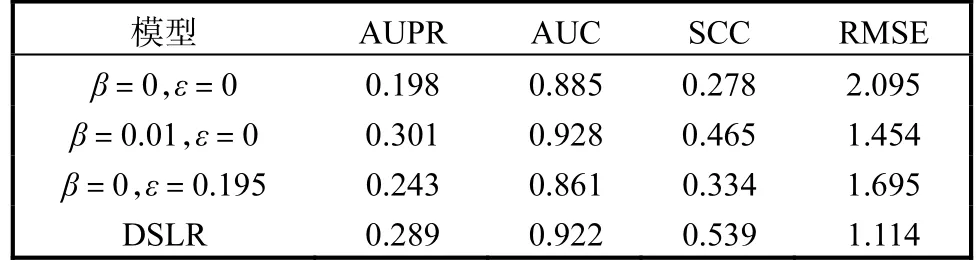
表3 消融實驗的比較結果 Tab.3 Comparison results of ablation experiments

3.4 上市后副作用預測

對于基準數據集的750種藥物和994種副作用，本研究發現評級矩陣M的未知副作用中，有9288種藥物-副作用關聯在SIDER數據庫中被標記為“上市后”(以下簡稱上市后副作用).這些上市后副作用由于在臨床試驗中并沒有發現，被認為頻率為1，即罕見的副作用[13].使用M中所有已知頻率類別(頻率＞0)作為訓練集訓練模型，然后對上市后副作用進行預測.圖4給出了未知副作用(頻率＝0)和上市后副作用預測值的PDF，以及基于10折交叉驗證M中罕見(頻率＝1)副作用預測值的PDF.結果表明：對于9288種上市后副作用，有31.52%被正確地預測為罕見，62.34%被預測為罕見或少見(頻率＝2)，82.82%被識別為有藥物-副作用關聯，說明DSLR模型對上市后副作用有較好的預測能力.

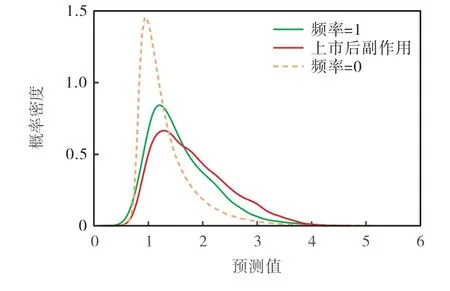
圖4 頻率＝1、頻率＝0及上市后副作用的概率密度函數Fig.4 PDF of predicted values for frequency＝1，frequency＝0 and post-marketing side effects

本研究隨機選取了藥物舒尼替尼，在SIDER數據庫中該藥物有51個副作用在上市后被發現.對于這些副作用，預測結果表明86.27%被識別為有藥物-副作用關聯，其中54.9%被識別為罕見(頻率＝1)，21.57%被識別為少見(頻率＝2)，9.8%被識別為不經常(頻率＝3).

4 結 語

本文提出了一種預測藥物副作用頻率的機器學習模型DSLR.基于基準數據集，DSLR模型將藥物之間的化學結構相似度和藥物頻率譜的余弦相似度的平均值作為藥物的相似度，副作用頻率譜的余弦相似度作為副作用的相似度，采用基于拉普拉斯正則化的非負矩陣分解模型，并引入超參數控制未知副作用標簽及其預測值的間隔.結果表明，DSLR模型不僅能準確預測藥物副作用發生的頻率，并且能夠對上市后藥物副作用進行預測，這有助于指導藥物風險-效益評價.

參考文獻：［1］ GODAT S，FOURNIER N，SAFRONEEVA E，et al.Frequency and type of drug-related side effects necessitating treatment discontinuation in the Swiss Inflammatory Bowel Disease Cohort[J].European journal of gastroenterology & hepatology，2018，30(6)：612-620.

［2］ CONCATO J，SHAH N，HORWITZ R I.Randomized，controlled trials，observational studies，and the hierarchy of research designs[J].The New England journal of medicine，2000，342(25)：1887-1892.

［3］ BANDA J M，EVANS L，VANGURI R S，et al.A curated and standardized adverse drug event resource to accelerate drug safety research[J].Scientific data，2016，3(1)：160026.

［4］ PIRMOHAMED M，JAMES S，MEAKIN S，et al.Ad- erse drug reactions as cause of admission to hospital：prospective analysis of 18 820 patients[J].British medical journal，2004，329(7456)：15-19.

［5］ CAMI A，ARNOLD A，MANZI S，et al.Predicting adverse drug events using pharmacological network models[J].Science translational medicine，2011，3(114)：114-127.

［6］ WANG Z，CLARK N R，MA’AYAN A.Drug-induced adverse events prediction with the LINCS L1000 data[J].Bioinformatics，2016，32(15)：2338-2345.

［7］ CAKIR A，TUNCER M，TAYMAZ-NIKEREL H，et al.Side effect prediction based on drug-induced gene expression profiles and random forest with iterative feature selection[J].The pharmacogenomics journal，2021，21：673-681.

［8］ GALEANO D，LI S，GERSTEIN M，et al.Predicting the frequencies of drug side effects[J].Nature communications，2020，11(1)：4575.

［9］ ZHAO H，ZHANG K，LI Y，et al.A novel graph attention model for predicting frequencies of drug-side effects from multi-view data[J].Briefings in bioinformatics，2021，22(6)：239.

［10］ KUHN M，LETUNIC I，JENSEN L J，et al.The SIDER database of drugs and side effects[J].Nucleic acids research，2016，44(1)：1075-1079.

［11］ LI T，DING C.The relationships among various nonnegative matrix factorization methods for clustering [C]//IEEE.Sixth International Conference on Data Mining(ICDM’06).New York：IEEE，2006：4053063.

［12］ ZHANG M，CHEN Y.Inductive matrix completion based on graph neural networks[EB/OL].[2022-01-25].https://arxiv.org/abs/1904.12058.

［13］ TATONETTI N P，YE P P，DANESHJOU R，et al.Datadriven prediction of drug effects and interactions[J].Science translational medicine，2012，4(125)：125-131.