分布式能源資源的通用數字孿生體構建與模擬方法

原啟濤，李志勇，燕續峰，肖居承，何光宇

（1.上海交通大學 電力傳輸與功率變換教育部重點實驗室，上海 200240；2.海南省電力學校，海南 海口570203）

0 引言

分布式能源資源（DER）包含可控負荷、分布式光伏、風機、儲能等，有效利用DER不僅能夠平抑波動和降低系統峰谷差，而且具有可觀的社會效益和經濟效益[1]。隨著DER數據源的異構性、海量性、隨機性趨于復雜，通過物理建模方法估量其運行穩態和暫態的難度和成本越來越高[2]。

數字孿生（Digital Twin，DT）為DER的模擬測試和運行優化提供了新的思路[3]～[5]。文獻[6]～[9]設計了電力系統DT的系統框架、組建模塊、通信架構和規約及應用案例。文獻[10]指出提出了負荷DER功率變化轉移模型，描述了電器狀態、功率與事件的關系。文獻[11]提出了以數據采集-事件檢測-特征提取-負荷分類-負荷識別為流程的負荷模型構建方法。文獻[12]則關注于負荷DER的高頻特征，如暫態電流、電壓-電流軌跡等，借此刻畫負荷DER的運行特性。文獻[13]，[14]提出了基于超狀態概念的負荷運行狀態模型及改進方法，極大地簡化了模型并提高了求解效率。文獻[15]提取了負荷DER的開啟、關閉時間和持續時長等關鍵因素作為額外特征用于負荷模型構建。文獻[16]針對一階隱馬爾科夫 （Hidden Markov Model，HMM）模型弱時間特性的特點，提出了一種負荷DER的時間特性模型，更直觀地表述了用戶用電習慣。對于分布式光伏、風機、儲能等DER，現有文獻主要針對其供電特性進行建模與研究。文獻[17]針對光伏等新能源出力的不確定性，提出了一種基于變分自編碼器和條件生成對抗網絡聯合結構的不確定性建模方法。文獻[18]采用改進的遺傳算法建立了實際雙饋風電機組的全運行工況下快速啟動的精確電磁暫態仿真模型。文獻[19]運用戴維南定理和模擬受控電流源對儲能電站進行等值仿真建模。上述文獻大多針對某一類DER進行建模，缺乏一種通用的DER模型對其穩態運行特性及暫態轉移過程進行統一精準描述，也缺乏相應的DER數字孿生體模型的運行模擬方法。

本文提出了DER的通用數字孿生體構建及模擬方法，并通過功率模型對穩態進行統一分解與描述，建立了多類暫態概率矩陣，對DER暫態過程及產生條件進行統一描述，給出了通用的DER數字孿生體模型及其運行模擬方法。算例對常見的DER進行了運行模擬測試，驗證了所提方法的有效性。

1 DER數字孿生體的通用穩態模型

1.1 DER穩態的功率成分

根據WOLD分解定理[20]，DER運行功率分解為規律成分和噪聲成分。DER的功率曲線P（t）為

1.2 DER通用穩態模型

本文將DER穩態功率定義為規律成分和噪聲成分的疊加結果，應當對這兩種成分區別建模。

1.2.1 DER穩態功率的規律成分建模

①線性規律模型

DER線性規律模型為

1.2.2 DER穩態功率的噪聲成分建模

將DER功率解耦為規律成分和噪聲成分后，其中的噪聲成分會受到各類外生、內生因素的影響，當隨機因素獨立時，依據中心極限定理，可近似認為噪聲成分服從高斯分布[21]，即：

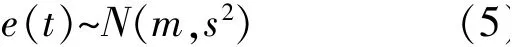
式中：m為噪聲成分的平均值；s為噪聲成分的標準差。

2 DER數字孿生體的通用暫態模型

2.1 DER暫態模式

DER的運行是穩態與暫態交替出現的，通常暫態過程持續時間很短，DER絕大部分時間處于穩態運行[20]。因此，暫態主要指DER穩態間的轉移，同時包含了其間的過渡態過程。根據影響暫態的主體可以將DER的暫態模式分為外界主導和自身主導兩類。

2.2 DER通用暫態模型

針對傳統HMM的弊端，本文提出DER通用暫態模型，包括暫態概率矩陣T、時長型暫態概率矩陣T1、時刻型暫態概率矩陣Tt及頻次型暫態概率矩陣Tf等部分，以全方位地描述各類DER在各種情況下的暫態轉移概率，以便于支撐數字孿生的平行測試功能。

2.2.1 暫態概率矩陣暫態概率矩陣T=[tij，1≤i，j≤N]刻畫了DER在暫態過程中轉向各種穩態的轉移概率。不同于傳統HMM中的轉移矩陣，在本暫態模型中，暫態概率矩陣T的對角元均為0，即不考慮DER的自身向自身穩態的轉移（即不轉移）的情況，因為已經發生了暫態是T的前提。

從DER的T矩陣中，可以看出暫態的所有情況及對應的發生概率，但是仍缺乏信息描述DER會在何種條件下發生暫態。由于DER的暫態具有很強的時間相關性，因而還須從時間概率的角度上描述DER的暫態情況。

2.2.2 時長型暫態概率矩陣

考慮到DER運行規律性和運行模式的固定性，穩態持續時間的變化將保持在一定范圍內。本文提出時長型暫態概率矩陣T1，以描述DER暫態轉移的持續時間概率分布。用高斯分布對該暫態過程進行建模，時長型暫態概率矩陣T1的數學表達式為

2.2.3 時刻型暫態概率矩陣

轉入型穩態通常由外界主導，通常一種時刻型穩態的轉移可以在一天的不同時段內發生多次，通常具有多峰性。由于高斯分布刻畫這種行為將產生極大的失真，因此，本文采用高斯混合模型（Gaussian Mixture Model，GMM）對時刻型DER的穩態轉移時刻分布進行建模。高斯混合模型形式為

式中：G（θij）為時刻型穩態i向穩態j型轉移時刻高斯混合模型；θij為模型參數；Si為由所有轉入型穩態構成的集合，類似的So為轉出型穩態集合。

Tt的元素G（θij）分布以1 d為周期，描述了DER從穩態i切換至穩態j在1 d時段上的概率分布。

2.2.4 頻次型暫態概率矩陣

利用Tt可以描述用戶對某些DER時的使用習慣，但其中的GMM以1 d為周期，其只能反映用戶在1 d之內使用DER的時間偏好，而不能反映1 d內用戶使用DER的次數和頻度。本文提出頻次型暫態概率矩陣Tf，用于刻畫用戶1 d內使用DER而產生的暫態的頻率次數，其數學表達式為

式中：N（mij，sij2）為DER在1 d內從i穩態轉移至j穩態的頻率高斯分布。

3 DER數字孿生體的運行模擬方法

3.1 DER的通用數字孿生體模型

穩態模型參數反映了DER穩態內功率變化情況及對應物理作用，其研究的時間尺度小，以解析模型為主，可以準確刻畫DER功率；暫態模型參數反映了用戶及DER的行為規律，研究時間尺度大，以概率模型為主，可以推斷DER暫態事件的概率。模型兩部分相互影響、交替產生作用，共同描述了DER的運行規律。基于DER的數字孿生體模型可以實現多種應用功能。利用穩態模型參數可以實現DER的功率短期預測、DER的狀態識別、異常狀態監測、用電數據壓縮和運行模擬等功能。DER的暫態模型參數可以實現DER功率的長期預測、用戶用電行為分析等功能。

3.2 通用數字孿生體模型參數提取

3.2.1 穩態模型參數提取

穩態參數包括穩態數量N、各穩態的趨勢功率模型S（t）、干擾噪聲模型e（t）。根據功率片段聚類方法可確定穩態數量N及每個穩態對應的功率片段樣本。

各穩態的趨勢功率模型S（t）及干擾噪聲模型e（t）提取方法如下。

①對于DER的某一個穩態n，屬于該穩態的功率片段樣本集合為P（n）=[P1（n），P2（n），…，Pm（n）]，集合中穩態n的樣本按照序列長度遞減排序，P1（n）為穩態n持續時間最長的功率序列，并指定該序列初始點對應時刻t=0，進而得到該序列任意點對應的時刻。將其他所有的序列樣本與該序列對齊，得到其他各序列對應得初始時刻，進而可以得到序列任意功率點對應的時刻。

②在得到了樣本集P（n）中每一個功率點對應的時刻后，可以獲得DER穩態n的時間-功率樣本點集Pc（n）=[（t1，p1（n）），（t2，p2（n）），…，（tm，pm（n））]。選取擬合誤差最小的模型作為DER穩態模型。

③利用S（n）（t）對時間-功率樣本集中的點進行模型估計，可以得到樣本估計偏差Pe（n）=[P（n）1，error，P（n）2，error，…，P（n）m，error]。 對偏差樣本進行正態分布擬合即可得到穩態n的干擾噪聲模型e（n）（t）。

3.2.2 暫態模型參數提取

暫態模型參數包括暫態概率矩陣T、時長型暫態概率矩陣T1、時刻型暫態概率矩陣Tt、頻次型暫態概率矩陣Tf與轉移類型集Si及So。DER的轉移類型可以在人工標注實際物理工作穩態時一并完成，進而得到Si及So。

①暫態概率矩陣T

初始化T為零矩陣，根據DER歷史運行記錄找出所有的穩態轉移，形成DER的穩態轉移樣本集St=[（1→i，t1），…，（i→j，tn），…]，其中i→j表示DER從穩態i切換至穩態j的轉移，tn表示這次穩態轉移發生的時刻。對于St中的每一次穩態轉移，令暫態概率矩陣T中的元素tij=tij+1。在遍歷了穩態轉移樣本集St中每一個元素后，對T的每行進行歸一化：

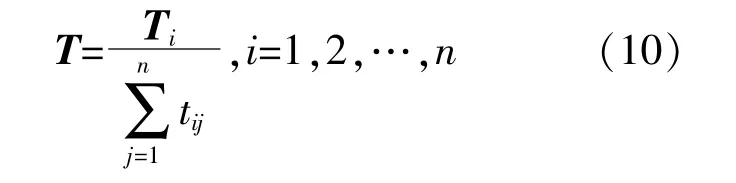
式中：Ti為穩態i向其他穩態轉移的頻率行向量。

②時長型暫態概率矩陣T1

對于轉出型穩態n，可以由其功率樣本集P（n）=[P1（n），P2（n），…，Pm（n）]得到該穩態的持續時間集T1（n）=[T11（n），T12（n），…，T1m（n）]。 提取持續時間集的均值及方差得到該穩態時長型暫態概率分布T1n=N（mn，sn2）。

③時刻型暫態概率矩陣Tt

對于轉入型穩態i，從中找到所有由該穩態轉移至其他穩態的子樣本集St（i）=[（i→j，t1），…，（i→k，tn），…]。并根據St（i）中轉入穩態的情況進一步將其劃分為多個同類型穩態轉移的子樣本集St，j（i）=[（i→j，t1），…，（i→j，tn），…]，S（i）t，j+1，…，j=1，2，…，n，j≠i。

同類型穩態轉移子樣本集St，j（i）包含所有穩態轉移i→j發生的時刻樣本。由于轉入型穩態轉移時刻分布以一天為周期，因此需要對集合里的時間元素進行處理，得到只包含24時計時的同類型穩態轉移時間集St，j（i）=[t′1，t′2，…，t′n]。用GMM對其中的元素進行擬合，獲得穩態轉移i→j的轉移時間概率分布G（θij）。

在采用GMM擬合時采用α-EM算法[22]，[23]，對每個同類型穩態轉移子樣本集進行擬合后，得到轉入型穩態i的時刻型暫態概率分布矩陣Tt,i=[G（θij），j=1，…，n，j≠i]。

④頻次型暫態概率矩陣Tf

頻次型暫態概率矩陣Tf刻畫DER在一天的周期內發生穩態轉移的次數。同類型穩態轉移子樣本集Stj（i）包含所有穩態轉移i→j發生的時刻樣本。對集合里的時間元素進行處理得到穩態轉移i→j在歷史記錄的時間范圍內每日的轉移頻數集合Stj″（i）=[cd1，cd2，…，cdn]。提取集合內元素的均值方差得到該穩態轉移i→j的頻率分布N（mij，sij2）。

在對每個同類型穩態轉移子樣本集進行了擬合后可以得到轉入型穩態i的轉移頻率矩陣Tf，i=[N（mij，sij2），j=1，…，N，j≠i]。

3.3 DER數字孿生體的運行模擬方法

DER數字孿生體的運行模擬在DER靈活性感知、評估、挖掘、調控和促進新能源消納等方面具有重要作用[12]，[24]，[25]。同時，DER運行模擬產生的數據還可以擴充已有數據集大小，用于機器學習模型的訓練，模擬生成的DER運行數據，在某些條件下還具有正則化效果[26]，有利于降低機器學習模型預測的誤差。

本文提出DER數字孿生體的運行模擬算法，能夠模擬未來待預測時間段內DER穩態持續和暫態轉移情況，進而通過各穩態的功率模型生成預測功率。圖1展示了DER運行模擬算法的流程。

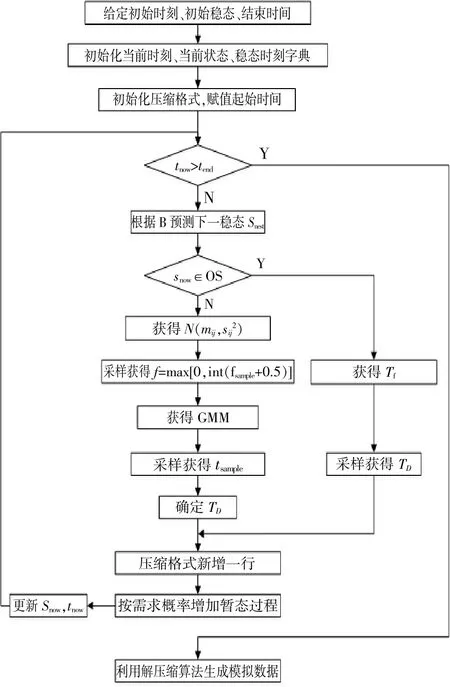
圖1 DER數字孿生運行模擬算法流程圖Fig.1 Flow chart of DER digital twin operation simulation algorithm

4 算例測試

本文以分布式能源資源中占比較高的空調負荷為例，說明提出的數字孿生體構建及模擬過程，并對所提方法對典型DER（風、光出力和充電樁的放電功率）進行模擬，其對比數據源于PJM開源數據集。基于本文所提出的DER通用數字孿生體模型及其運行模擬方法，生成1 d的DER運行模擬數據。

4.1 構建及模擬過程

某定頻空調5 d的歷史功率曲線如圖2所示。

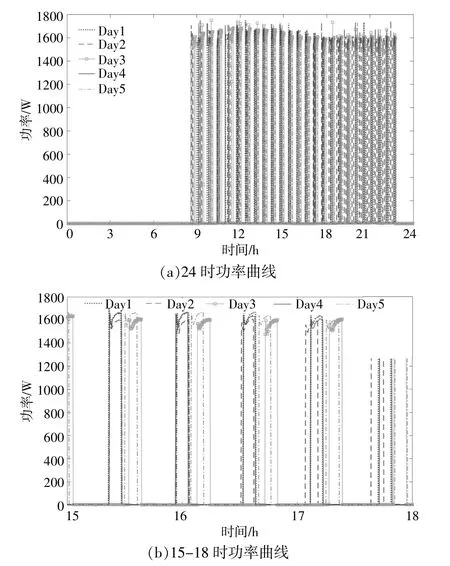
圖2 某空調5 d的歷史功率曲線Fig.2 5 day historical power curve of an air conditioner

采樣頻率為15 s/次，由于采集時間為夏季，故提取的空調穩態不包含制熱。利用歷史運行功率數據得到的該空調模型的穩態參數如表1所示。

表1 空調模型穩態參數Table 1 State parameters in air conditioner's model

由圖3可以看出，空調平均每次制冷時間在10 min左右。從時刻型暫態概率和頻次型暫態概率分布來看，空調穩態轉移的次數平均約為23次/d，運行時間分布在9～23時內。

圖3 空調模型的暫態參數Fig.3 Transient parameters of air conditioning model

圖4為前文提出的運行模擬算法得到的功率曲線與空調歷史數據中最接近的功率曲線對比。圖中模擬數據與歷史數據之間的絕對誤差為5.3%。

圖4 空調數字孿生運行模擬結果Fig.4 Simulation results of air conditioning digital twin operation

由圖4可以看出，由模擬算法得到的功率曲線大體上準確模擬了空調典型周期運行的特點。

4.2 DER運行模擬測試

在運行環境為Inter CORE I7 8th Gen，各個模擬時間均在1 s內，采用本文所提出的數字孿生運行模擬算法生成了其他幾種常見DER的功率曲線，并與其歷史數據的對比，如圖5所示。

圖5 DER數字孿生運行模擬結果Fig.5 Result of DER digital twin operation simulation

由圖5可知，各子圖中模擬數據與其最接近的歷史數據之間的絕對誤差分別為4.3%，4.1%和3.7%，驗證了所提方法的有效性，表明所提算法時效性可支撐實時運行模擬。由模擬方法生成的DER運行數據與DER實際歷史運行數據相比，在開始時間、持續時間及穩態功率等方面曲線形態均十分接近，具有良好的相似程度。本文方法不僅能夠在大體上準確模擬光伏出力晝盈夜虧、風機的反調峰特性、充電樁的典型時空分布情況，而且在細節的運行模擬上（例如噪聲成分幅值、穩態功率波動幅度、暫態過渡功率）也與歷史數據具有較高的相似程度。該算例測試結果可以說明本文所提出的DER數字孿生體模型及其運行模擬技術能夠支撐數字孿生世界的高精度鏡像映射和平行測試功能。

5 結語

本文對DER通用數字孿生體模型進行了詳細分析，對DER穩態的功率成分進行了分析并建模；隨后對DER暫態進行了研究并建模，從而輔助電力系統調控中定制有序的發用電計劃，減少棄風棄光，促進可再生能源的大規模消納。后續研究將基于所提出的通用數字孿生體模型，構建虛擬的智能用電網絡人機交互平臺；基于數字孿生技術，直接基于真實系統數據來模擬各種運行策略下系統運行情況，并評價運行策略的經濟性和安全性等，以提高可再生能源的消納為目標，指導真實系統的運行調度，為實際運行直接提供參考。