基于殘差協方差的配網多個不良量測辨識與仿真

陳少雄

（三峽大學 電氣與新能源學院，湖北宜昌 443000）

引言

為滿足電力系統發展，保證其安全穩定經濟運行，必須建立完整而可靠的實時數據庫。如果通過增加硬件設施的數量和精度，在成本上的代價將會是難以想象；考慮到經濟效益，利用軟件手段進行完善，而狀態估計技術充分利用了現有設備，通過算法原理使數據精度得到提高，測點和量測項目的不足得到彌補，非正確因素造成的數據被剔除，在不耗費巨資情況下使得實時數據庫的質量和可靠性大幅提高。而用于電力系統狀態估計的數據中，不可避免會出現不良量測數據。實際電力調度中心的能量管理系統（EMS）中雖都有比較可靠的狀態估計功能，但沒有專門的不良數據辨識與校正輔助決策軟件。目前針對這些不良量測數據，并沒有較好的辨識方法，一般是運維人員通過相關經驗進行辨識及查找原因[1,2]。因此針對網絡存在不良量測進行辨識研究具有重要意義。

1 基于殘差協方差的多個不良量測辨識

配網中不存在輸網電阻遠小于電抗的特性，為此引入復數歸一化理論，并利用殘差靈敏度理論進行量測的區塊劃分，采用正則化殘差理論實現多個區塊的不良量測辨識。

1.1 單位復數歸一化

傳統上，電力系統的參數和變量是按單位（pu）基歸一化的，在單位（pu）基上選擇電壓和功率基的實值。具體理論如下[3]：

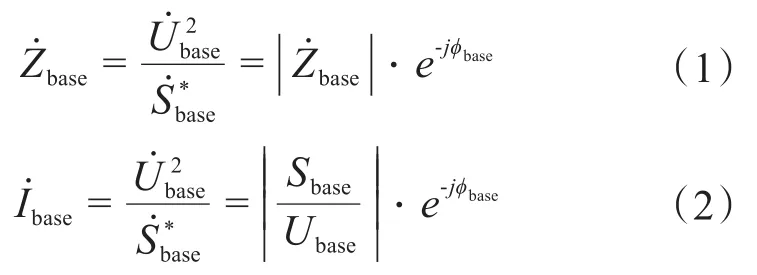
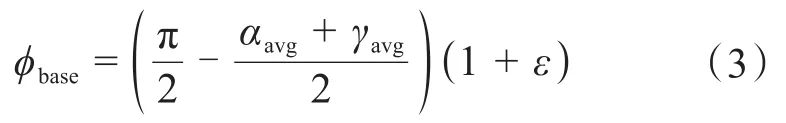
式中，αavg為平均R/X比，弧度；γavg為最大和最小R/X比的平均值，弧度；ε為功率因數指數。具體計算公式如下：

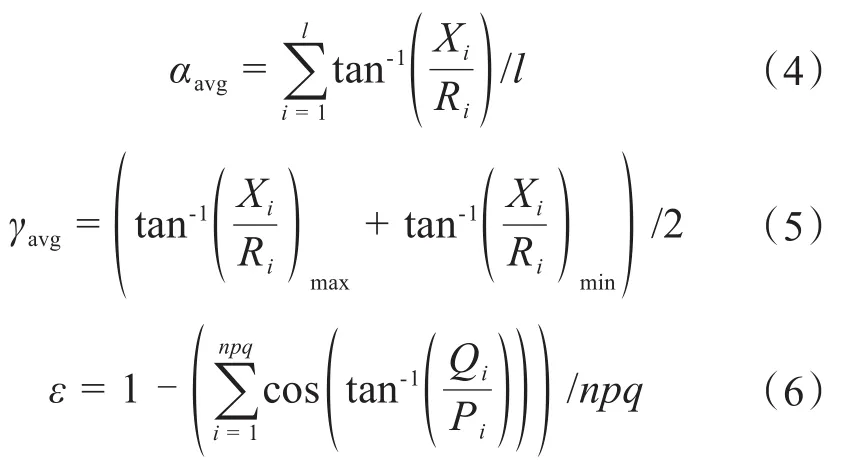
式中，l代表支路總數，Xi，Ri分別代表支路的阻抗，npq代表PQ節點個數，Pi和Qi分別代表負荷有功功率和無功功率。

原系統結構參數轉換：

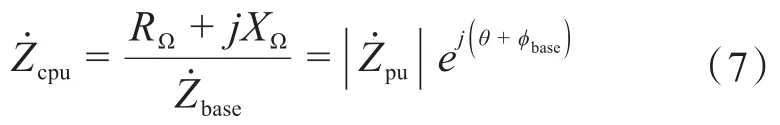
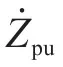
最終歸一化的電阻、電抗分別為：

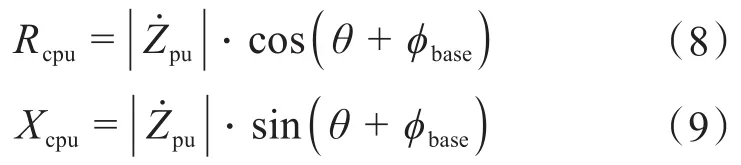
最終單位復數歸一化的有功和無功分別為：

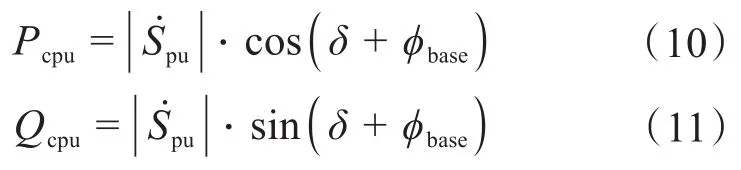
1.2 基于殘差協方差的量測分組

在正則化殘差檢測法中，殘差的協方差矩陣與殘差靈敏度矩陣的關系為：

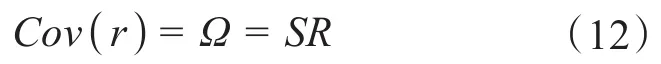
式中，r為量測殘差，S為殘差靈敏矩陣，R為權重矩陣的倒數。

殘差協方差矩陣內部元素可以表征多個殘差之間的關聯聯系，殘差之間關聯聯系也可以反映量測量實際誤差之間的關聯關系。如果殘差協方差矩陣中元素Ωij大于某閾值，那么意味著殘差i和殘差j之間存在非常大的聯系，反之亦然，進一步，意味著量測i和量測j存在很強的關聯性。基于此思想本文準備通過協方差先對各個量測進行強弱聯系的分組，然后對于各組進行最大正則化殘差檢驗，以達到多個不正常量測的同時甄別。

由于殘差協方差矩陣表征的是多個殘差之間的關系，為了更清晰地描述各個量測之間的聯系強弱，定義量測i和量測j之間的相關系數：

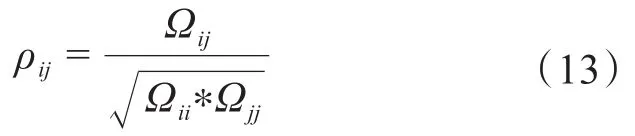
當ρij大于某一閾值時，認為量測i和量測j間的關聯關系較弱，而小于某一閾值時則認為關聯關系較強。也正是基于此原理，對量測進行分組。

首先，尋找量測與i有較強聯系的量測，并定義與量測i關聯強的集合：

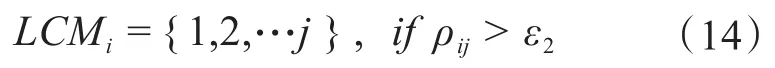
式中，ε2為關聯強弱判斷閾值。

由于多個組內可能會存在量測元素的重合，為避免量測元素重合導致量測集合重復判斷，對關聯量測集合LCM進一步分組：

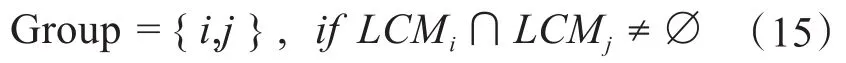
通過殘差協方差矩陣分析殘差之間關系，并遷移至量測之間的關系，再利用相關系數進行初步關聯集合元素的尋找，最后通過多個集合交集檢測實現多個不同組的劃分。

1.3 多個不良量測檢驗

劃分的目的是為了更好尋找出不同的不良量測。首先前文已經介紹了單位復數歸一化能夠較好地實現配網有功和無功的解耦，即意味著已經將有功和無功劃分至兩個組內分別進行，縮小了計算的規模，其中，有功量測指節點注入有功量測和支路有功率量測；無功量測值節點注入無功量測、節點電壓幅值和支路無功量測。從基于最大正則化殘差甄別原理可知：并不是所有的量測對應的殘差都大，因此可通過設定閾值篩選出可疑的量測，然后對可疑量測再分組即可進一步減小計算規模。

定義可疑量測集合SLCM，其判據為：

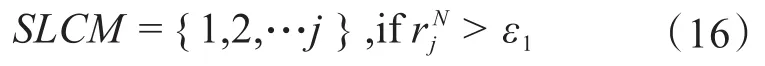
式中，ε1為可疑量測判斷閾值。

對每個可疑量測計算其LCM，再通過LCM劃分Group，最后應用最大正則化殘差檢測進行多個非正常量測的同時甄別。

2 仿真分析

2.1 仿真數據

采用IEEE30節點系統構造仿真場景，結構如圖1，數據見文獻[5]，系統結構參數見附錄。在算法過程中重新對各節點編號，編號原則：原有節點編號加1。模擬的量測數據采用潮流結果疊加高斯噪聲形成，電壓幅值、注入功率和支路功率的量測誤差標準差分別設為0.004、0.01以及0.008。

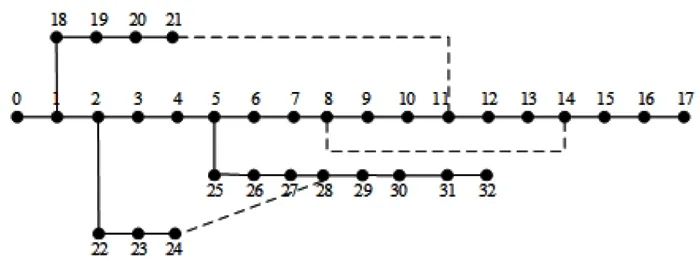
圖1 IEEE 33配電系統

不良量測如表1所示，有功無功不良量測辨識結果見表2。

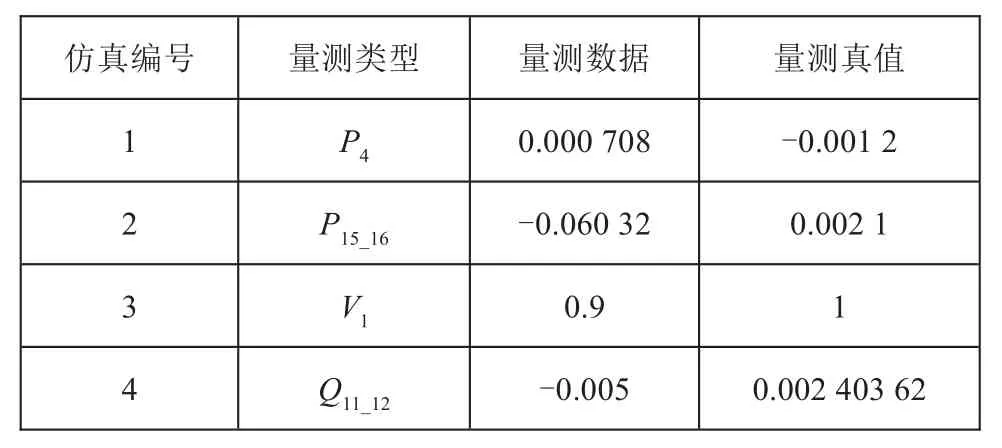
表1 有功和無功不良量測數據

從表2可知，算法總共劃分出4個組，第一組存在 3 個元素，分別為P4、P3_4和P4_5，P4對應的正則化殘差最大為4.250 0；第二組存在15個元素，分別為P10、P11、P12、P14、P15、P16、P17、P10_11、P11_12、P12_13、P13_14、P14_15、P15_16、P16_17和P17_18，其中P15_16、對應的正則化殘差最大為31.945 0；第三組內仍然存在一個元素V1；第四組內存在21個元素，分別為：Q7、Q9、Q10、Q11、Q12、Q13、Q14、Q15、Q16、Q17、Q18、Q8_9、Q9_10、Q10_11、Q11_12、Q12_13、Q13_14、Q14_15、Q15_16、Q16_17和Q17_18，其中Q11_12對應的正則化殘差最大為85.917 6；四個組內均正確甄別出了不良量測數據，表明即使在有功不良量測和無功不良量測同時存在時，本文所提算法均能有效實現多個不良量測的甄別。

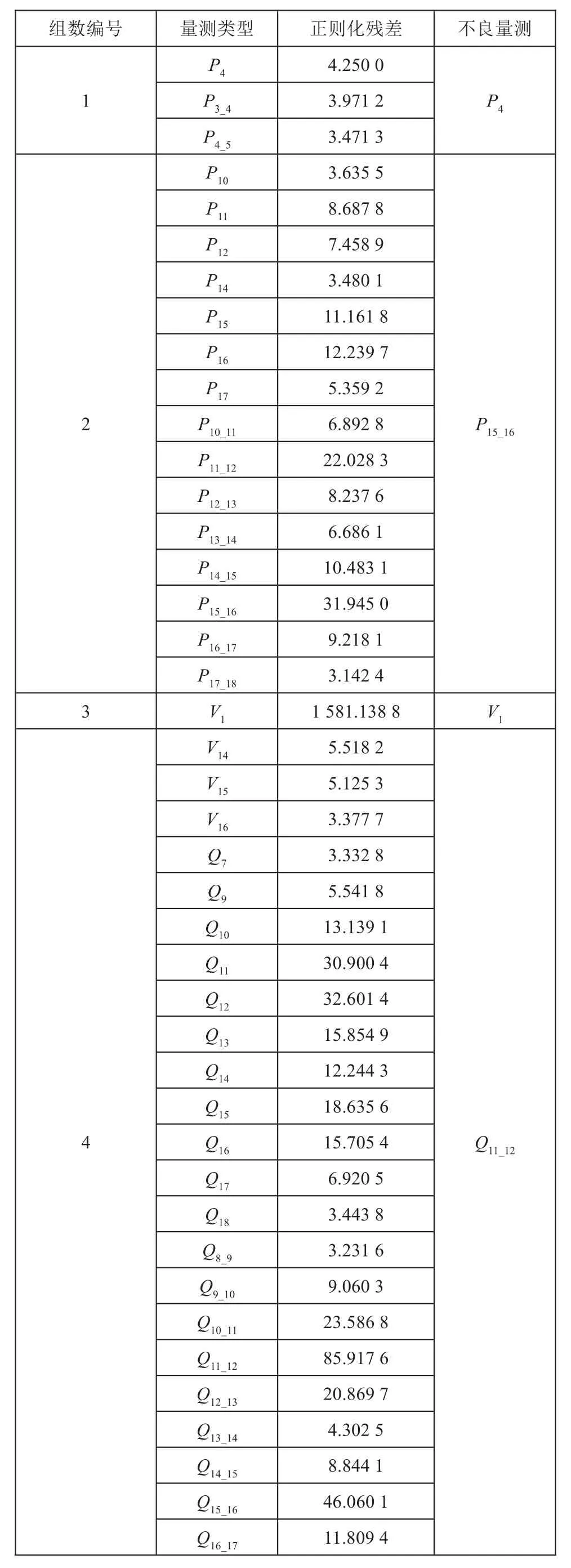
表2 有功無功不良量測辨識結果

4 結論

引入單位復數歸一化方法，將解耦狀態估計算法應用于配網中，實現有功和無功量測的分塊；基于殘差靈敏度劃分成不同組，并用最大正則化殘差同時甄別多個組內不良量測。利用IEEE33節點所構造的算例驗證了所提算法的正確性和快速性。