反思建構，讓“不等式”之樹枝繁葉茂

文／高榮興

一元一次不等式（組）是初中階段比較重要的內容。類比一元一次方程，我們把含有一個未知數且未知數的次數是1 的不等式叫作一元一次不等式。由幾個含有同一個未知數的一元一次不等式組成的不等式組就叫作一元一次不等式組。下面，我們一起來梳理一下本章的內容。

學習這一章，我們先要對不等式的性質進行研究。同學們在學習時要與等式的性質進行對比，弄清兩者的相同與不同之處。在了解了不等式性質的基礎上，我們再分兩個方面進行學習。一方面是對概念的學習，比如，在本章，我們要知道什么是一元一次不等式（組），什么是一元一次不等式的解和解集，一元一次不等式（組）的解集如何表示等。另一方面是對方法的學習，比如，如何解一元一次不等式（組），步驟有哪些；如何用一元一次不等式（組）解決實際問題，解決問題的關鍵是什么；等等。按照這個思路，我們就可以將本章“知識樹”的主干畫出來了（如圖1）。

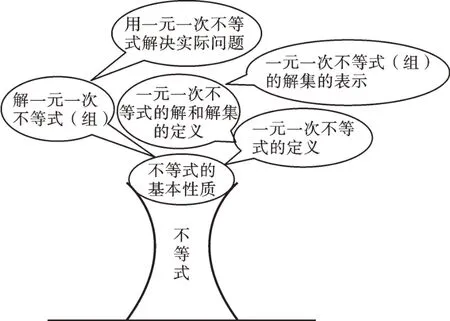
圖1

同學們在學習的過程中，還要結合著練習、運用，不斷反思建構，只有這樣，“不等式”之樹才會枝繁葉茂。接下來，我們來到不等式的應用，通過對典型例題的分析，體驗知識的生長。

例1已知x=2 是關于x的不等式x-3m+1≤0 的一個解，那么m的取值范圍為________。

一般地，能夠使一元一次不等式成立的未知數的值，叫作一元一次不等式的解。若這個值是不等式的解，則將該值代入，不等式成立。本題中，把x=2代入不等式，不等號仍成立，即2-3m+1≤0，進而可得m≥1。若已知條件變成“‘x=2’不是關于x的不等式x-3m+1≤0 的解”，要求m的取值范圍，該怎么做呢？請同學們自行思考。

例2（1）如果不等式組無解，則下列數軸示意圖正確的是（ ）。

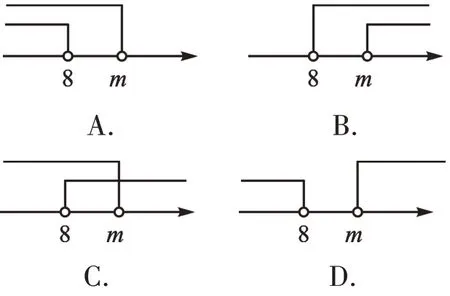
幾個一元一次不等式的解集的公共部分，叫作由它們所組成的一元一次不等式組的解集。要在數軸上表示出不等式組的解集，就要把每個不等式的解集在數軸上表示出來。數軸上的點把數軸分成若干段，如果數軸的某一段上面表示解集的線的條數與不等式的個數一樣，那么這段就是不等式組的解集。我們也可以通過口訣來確定不等式組的解集，即“同大取大，同小取小，大小小大中間找，大大小小解不了”。第（1）題中，因為不等式組無解，所以數軸上沒有兩條線段重合的區間，答案選D。第（2）題，因為原不等式組的解集是x≤2，所以根據“同小取小”，可以判斷“m＞2”，但我們發現“m=2”也符合題意，綜合起來可得“m≥2”。我們在解決類似問題時，都要注意“=”的問題。

例3（1）解不等式：x-≤2-，并把它的解集表示在數軸上。

（2）解不等式組：

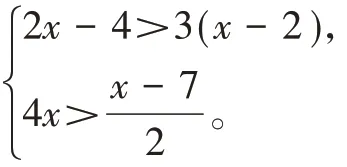
與一元一次方程的解法類似，解一元一次不等式一般也有去分母、去括號、移項、合并同類項、將項的系數化為1這幾步。但其中略有不同的是，在對一元一次不等式去分母和系數化為1 時，要注意不等號方向是否要發生改變。如果不等式的兩邊同時乘（或除以）同一個負數，不等號方向是要改變的。而解一元一次不等式組的步驟是：先分別求出不等式組中各個不等式的解集，再求出這些不等式的解集的公共部分，即這個不等式組的解集。確定不等式的解集的公共部分，我們可以借助數軸，也可以利用口訣。

（1）去分母，得6x-3（x-1）≤12-2（x+2），

去括號，得6x-3x+3≤12-2x-4，

移項，得6x-3x+2x≤12-4-3，

合并同類項，得5x≤5，

系數化為1，得x≤1。

在數軸上表示解集，如圖2所示。

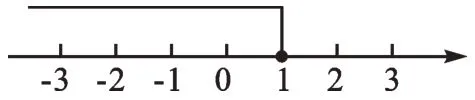
圖2

（2）解不等式2x-4＞3（x-2），得x＜2；解不等式4x＞，得x＞-1。借助數軸或利用口訣“大小小大中間找”可知，不等式組的解集為-1＜x＜2。

例4某市公交公司為落實“綠色出行，低碳環保”的城市發展理念，計劃購買A、B兩種型號的新型公交車，已知購買1 輛A型公交車和2 輛B型公交車需要165 萬元，購買2 輛A型公交車和3輛B型公交車需要270萬元。

（1）A型公交車和B型公交車每輛各多少萬元？

（2）公交公司計劃購買A型公交車和B型公交車共140 輛，且購買A型公交車的總費用不高于購買B型公交車的總費用，那么該公司最多購買多少輛A型公交車？

對于一元一次不等式應用題，解題的關鍵是找準數量之間的不等關系，然后設出未知數，正確列出一元一次不等式。（1）設A型公交車每輛x萬元，B型公交車每輛y萬元，由題意得解得答：A型公交車每輛45 萬元，B型公交車每輛60萬元。（2）設該公司購買m輛A型公交車，則購買（140-m）輛B型公交車，由“購買A型公交車的總費用不高于購買B型公交車的總費用”，列出一元一次不等式，得45m≤60（140-m），解得m≤80。答：該公司最多購買80輛A型公交車。