基于差分自回歸移動平均模型的醫用直線加速器劑量偏移預測研究

方園

安徽省第二人民醫院 （安徽合肥 230000）

時間序列為按照時間順序獲得的一系列觀測值的組合。隨著科學技術的不斷發展，對于時間序列的研究被應用于金融、氣象、農業生產等領域[1-3]。時間序列數據挖掘工作的主要任務是獲取數據中蘊含的與時間相關的信息，掌握事物發展的規律。通過對時間歷史數據的挖掘，我們可以預測未來一段時間可能發生的數據，并以此分析事物未來的發展趨勢[4]。

在放射治療中，醫用直線加速器是不可或缺的設備，其輸出劑量直接決定了患者治療的預期效果，因此，保證輸出劑量的穩定性非常重要[5]。由于醫用直線加速器是一類結構復雜的高精度大型醫療設備，某些元器件的故障或老化均會導致加速器輸出劑量發生突發的或緩慢的變化，因此，對加速器輸出劑量的日常安全監測成了放射治療質量保證（quality assurance，QA）工作的重點[6-7]。很多學者利用統計學處理方法開展了大量關于醫用直線加速器劑量穩定性的研究，且取得了較好的研究成果，為加速器劑量穩定性的監測工作提供了參考依據[8-10]。也有學者利用時間序列分析方法對醫用直線加速器質量穩定性進行了分析和預測，并證實了此方法在加速器劑量預測工作中的應用可行性[11]。鑒于此，本研究對醫用直線加速器質控工作中的劑量監測數據進行了研究，并利用時間序列挖掘知識進行了數據分析，以達到對加速器劑量偏移進行預測的目的。

1 數據來源

本研究的數據來源于我院放射治療中心醫科達precise 直線加速器，選取3個調整周期內共計66條加速器劑量實測數據作為實驗樣本。

2 研究方法

首先，選取1個調整周期內的前19條劑量監測數據作為原始研究數據，對其進行穩定性分析；然后，利用時間序列研究中常用的差分自回歸移動平均（auto regressive integrated moving average，ARIMA）模型對其進行建模并預測后5次的測量結果；最后，將預測結果與另外兩個測量周期用同樣預測方法得出的預測結果進行對比分析。

2.1 線性模型的建立

ARIMA 模型于1976年由Box 和Jenkins 等學者提出，之后被廣泛應用于經濟、金融和醫療等領域[12-14]。ARIMA（p，d，q）模型的通式為：

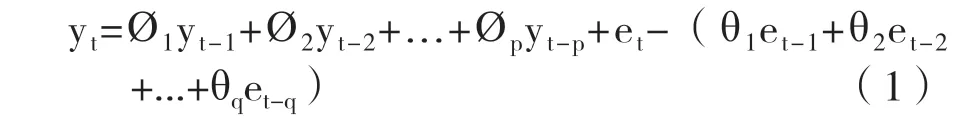
該模型分為前后兩部分，前部分?1yt-1+?2yt-2+...+?pyt-p是自回歸方程，后部分et-(θ1et-1+θ2et-2+...+θqet-q）是誤差移動方程，其中，yt是當前值，?1、?2...是自相關系數，θ1、θ2...是誤差系數，yt-1、yt-2...及et-1、et-2...是滯后項，et是誤差，p 是自回歸項數，q 為移動平均項數，d 為時間序列成為平穩時所作的差分次數。

2.2 應用ARIMA 模型對數據進行分析

存在一定發展趨勢的時間序列均是非平穩的，而ARIMA模型必須建立在平穩的基礎上才有意義[15]。因此，時間序列建模首先應去除確定性因素，包括趨勢和季節性因素，然后檢測剩下數據的平穩性，最終通過檢驗的數據才可進行ARIMA建模，建模的具體參數可以通過殘差自相關函數（autocorrelation function，ACF）和偏自相關函數（partial autocorrelation function，PACF）值來確定，R語言中有1個被命名為“auto.arima”的函數，可以用來直接定參，然后用此參數進行模型的擬合和預測[16]。

auto.arima 函數是Hyndman-Khandakar 算法的1個變種，其結合了單位根檢驗、最小化赤池信息準則（Akaike information criterion，AIC）和極大似然估計（maximum likelihood estimate，MLE）等評價標準來獲得1個ARIMA 模型。

Hyndman-Khandakar 自動ARIMA 建模算法步驟如下：

步驟1：通過重復地進行單位根檢驗（Kwiatkowski Phillips Schmidt Shin test，KPSS）測試來確定差分階數d（0≤d≤2）。

步驟2：對數據差分d 次之后，通過最小化AIC來選擇最優的p，q；算法通過stepwise search 而不是遍歷所有可能的p，q 組合來尋找最優的p，q 組合。

2.3 數據驗證

我們通過對周期內的數據進行觀察，發現其呈現逐步上升的趨勢且不存在季節性因素，劑量實測數據序列見圖1。

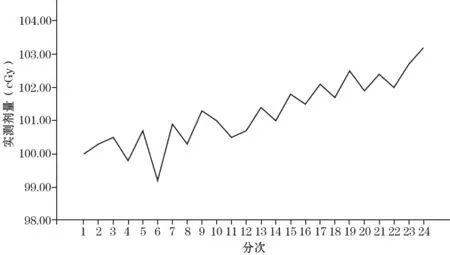
圖1 劑量實測

經過一階差分和R 語言中的auto.arima 函數，我們得到1個p，q 的最優組合，即ARIMA（1，1，0）。劑量預測模型的擬合預測見圖2。

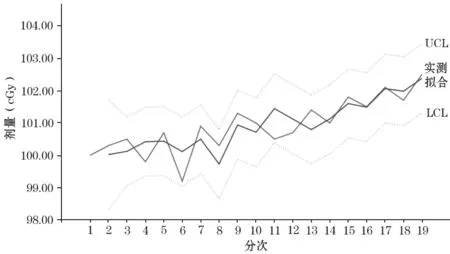
圖2 劑量預測模型的擬合預測

通過對預測模型的殘差ACF 和PACF 值的觀察，發現取值均在置信區間內，因此殘差檢驗可通過。預測模型的殘差ACF 和PACF 值見圖3；預測模型的參數估計見表1，由表可知，ARIMA（1，1，0）模型的參數在統計學上顯著。

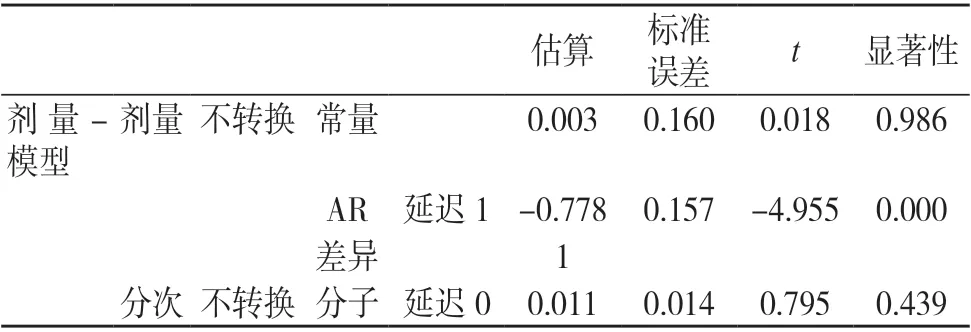
表1 ARIMA 模型的參數

圖3 預測模型的殘差ACF 和PACF 值

3 結果與分析

經過ARIMA 模型參數的選取、檢驗和確認，發現運用此模型獲得的在1個預測周期內的預測值能夠較好地反映醫用直線加速器劑量變化的范圍和趨勢，預測結果見圖4和表2。表2是周期內第20～24次的劑量預測值與實測值的對比，通過對比可知，預測值對實測值有較好的體現，預測誤差為0.18%～0.80%。

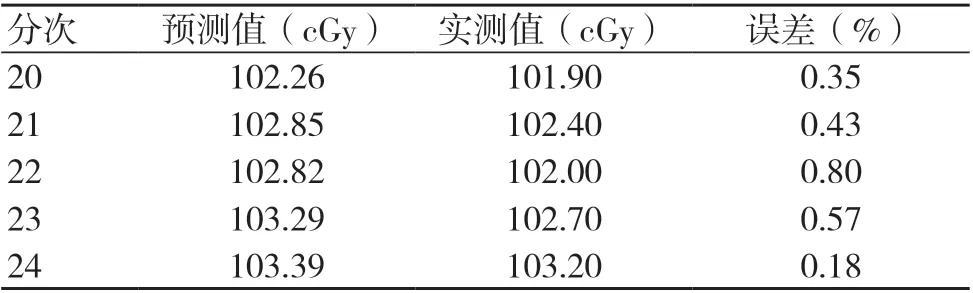
表2 劑量預測數據與實際數據的對比

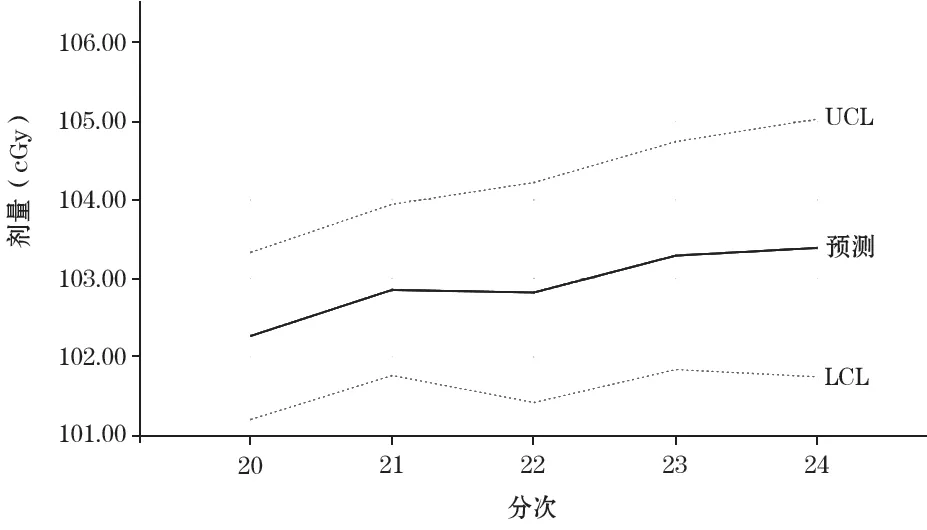
圖4 劑量預測值

在對數據結果進行總結時，我們發現預測是基于1個固定周期內的數據進行的，為了明確ARIMA模型在其他周期內的數據表現，本研究就此增加了兩個測量周期的數據并用上述方法進行了預測和對比，發現ARIMA（1，1，0）模型對其他測量周期的數據預測也具有較好的表現。周期二、三的預測結果見圖5和表3。表3中周期二、三分別代表的是兩個測量周期第20～24次的實測值和預測值，由表可知，運用此模型兩組預測值與實測值的對比表現良好，誤差為-1.28%～0.50%。

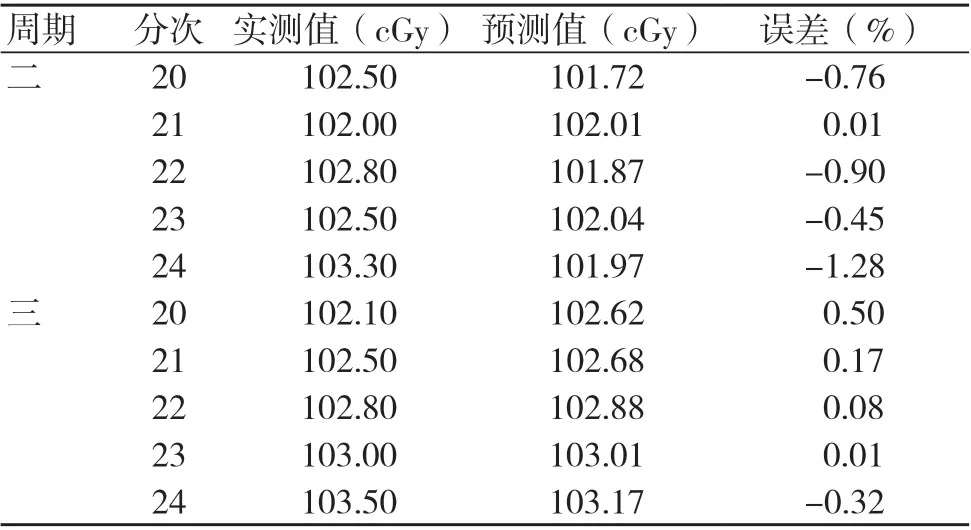
表3 周期二、三劑量預測數據與實際數據的對比

4 小結

本研究提出的利用時間序列進行醫用直線加速器劑量預測方法，具有較好的預測精度，對加速器劑量參數的及時調整起到了參考和提示作用。但是，ARIMA 模型也存在一定的局限性，僅適用于正常檢測和調整內的數據預測，當醫用直線加速器出現維修和保養，且維修和保養的項目影響到劑量輸出時，此模型將不再適用，檢測周期應以維修和保養后的時間開始計算。