山區鋼箱梁懸索橋抗風性能研究★

徐 茂，裴 城

(1．蘇交科集團股份有限公司，江蘇 南京 210019; 2．西南交通大學，四川 成都 610000)

不同于平原地區，山區峽谷地區風環境復雜，受地形影響較大，山區風參數的確定也不能按照平原和跨海大橋一樣按規范直接計算。另一方面，大跨懸索橋由于跨度大、阻尼低、剛度小，是風致振動的敏感結構，在強風的作用下，容易出現顫振現象，在常見風速下容易出現較大振幅的渦激振動，因此抗風性能成為懸索橋設計和建造中的關鍵問題之一[1-2]。我國公路橋梁抗風設計規范和日本、美國、英國等相關規范[3]，對跨度超過200 m 的大跨度橋梁建議通過專門的抗風性能研究，以確保大橋的抗風安全和運行舒適度，對不符合設計要求的斷面形式，提出可行的抗風措施[4]。

1 工程背景

某大跨鋼箱梁公路懸索橋，位于紅河州建水(個舊)至元陽高速公路上，主橋為單跨懸索橋，主跨700 m，大橋在主梁兩端設置豎向支撐支座，為了限制橫向靜風位移設置了橫向抗風支座。為了限制大橋的縱向位移，減小縱向振動對吊桿疲勞的影響和增加伸縮縫的耐久性，在梁端設置了縱向黏滯阻尼器。主橋結構布置和主梁斷面如圖1 所示。

2 大橋設計風參數

橋位處于個舊與元陽之間，可以取周邊氣象站的參考數據，橋位距離規范列舉的氣象站蒙自、元江、文山距離較近，可以取蒙自或者元江的風速資料之間的較大者，根據國家氣象資料2015 年前的氣象資料和周邊地形環境，可以得到主梁高度處100 a 一遇的10 min 年最大平均風速為32．3 m/s。橋位地處山區峽谷，不能以常規的風速對數律或者指數律換算得到橋面設計基準風速，可以按照峽谷風速放大系數進行折算[5]。具體為:

其中，H為峽谷底部距離橋面的高度;B1為谷底寬度;B2為橋梁的受風長度。橋梁處于山區，可歸為D 類地表。根據我國相關橋梁設計規范，施工期可取10 a 重現期，該橋成橋與施工期間的風參數見表1。

表1 大橋設計風參數

3 結構動力特性分析

大跨橋梁在風的作用下，主風致振動主要是橫向、豎向和扭轉三個方向，必須建立三維有限元模型，才能全面反映橋梁結構的振動情況。由于大橋屬于細長結構，可以利用常見的魚骨式有限元模型，即整個鋼箱梁的剛度、平動質量和轉動質量都集中到扭轉中心的線性主梁上，主梁與吊桿的連接通過無質量的剛性梁(剛臂)相連。橋塔和輔助墩采用一般的梁單元，吊桿和主纜采用只承受拉力的桿單元，并考慮重力剛度(初始拉力) 的影響。表2 給出了影響該橋抗風性能的幾個關鍵振型的計算結果。

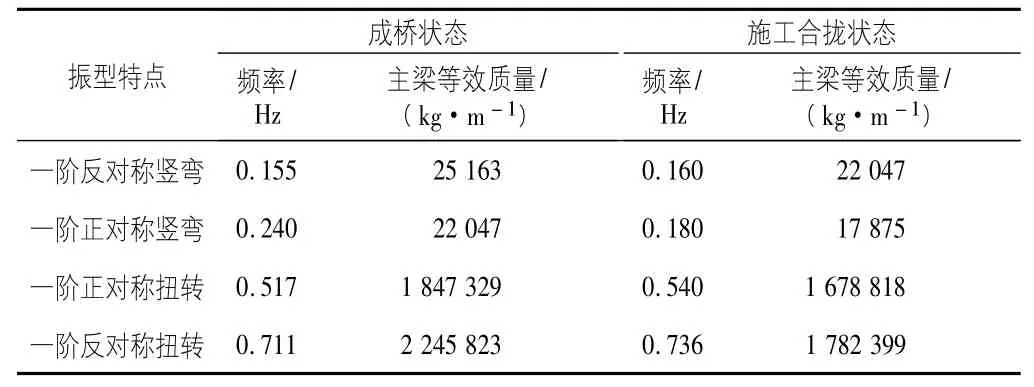
表2 大橋的主要振型、頻率和等效質量

4 靜力三分力系數

主梁靜力三分力系數是研究橋梁抗風性能的基礎，一般是通過主梁剛體節段模型風洞獲取。研究表明，在均勻流中得到的三分力系數偏于安全，因此橋梁三分力系數的試驗均在均勻流場中進行。通過節段模型得到模型受到的風力，反算得到主梁的三分力系數。根據公路橋梁抗風設計規范，一般試驗的風攻角為-10° ～10°。在體軸坐標系中的試驗結果如圖2 所示。在體軸坐標系中，以試驗時的水平方向為橫軸，豎向為縱軸。從圖2 中可以看出，主梁升力系數斜率為正，說明斷面具備氣動穩定的必要條件。主梁在0°攻角下阻力系數為0．64，從而表明流線箱型橋梁斷面具有較小的風荷載，這也是流線型鋼箱梁的主要優點。主梁力矩系數接近于0，受攻角影響較小。

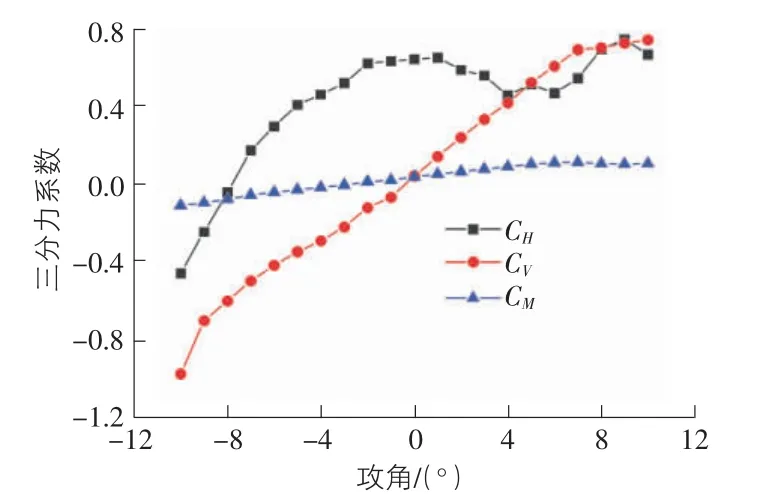
圖2 主梁三分力系數隨攻角的變化曲線

5 主梁顫振性能試驗

橋梁的顫振是在平均風作用下的一種具有破壞性的發散振動，其振動機理為在平均風速下，振動的橋梁與周邊氣體之間不斷的相互作用，并從風中吸收能量，致使振幅越來越大，直至結構破壞。因此主梁的顫振問題是必須解決的問題，必須保障在大橋遇到的風速范圍內不會發生顫振，即顫振臨界風速必須大于顫振檢驗風速。顫振臨界風速一般通過有限元分析、節段模型風洞試驗和全橋模型風洞試驗進行。一般情況下，節段模型風洞試驗的結果偏于安全，可利用節段模型風洞試驗進行氣動外形的優化，提出改善顫振性能的氣動措施。

節段模型一般用8 根彈簧模擬豎向和扭轉兩個自由度，模擬主梁的豎向和扭轉振動。模型縮尺比一般采用1∶50，模型本身必須有一定的剛度，防止局部振動，并保證長寬比大于2。試驗裝置和試驗照片如圖3 所示。

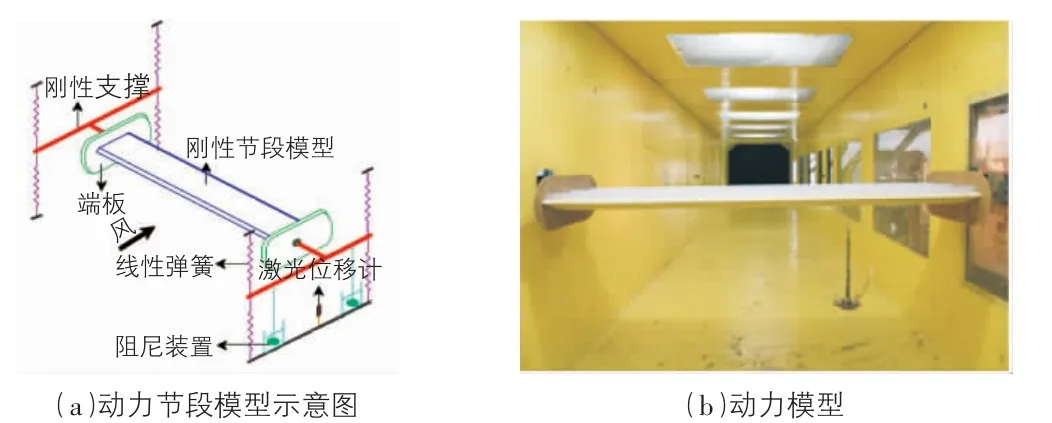
圖3 動力節段模型試驗

流線箱梁懸索橋的成橋狀態由豎彎基頻和扭轉基頻控制; 同時受扭彎頻率比影響顯著，扭彎頻率比越小，發生顫振的可能性更大。為選擇正確的計算參數，需要針對橋梁的對稱振型和反對稱振型進行對比。經計算，該橋的正對稱扭轉頻率與正對稱豎彎頻率的比值較小，試驗只針對正對稱振型進行。

模型模擬的試驗參數見表3。

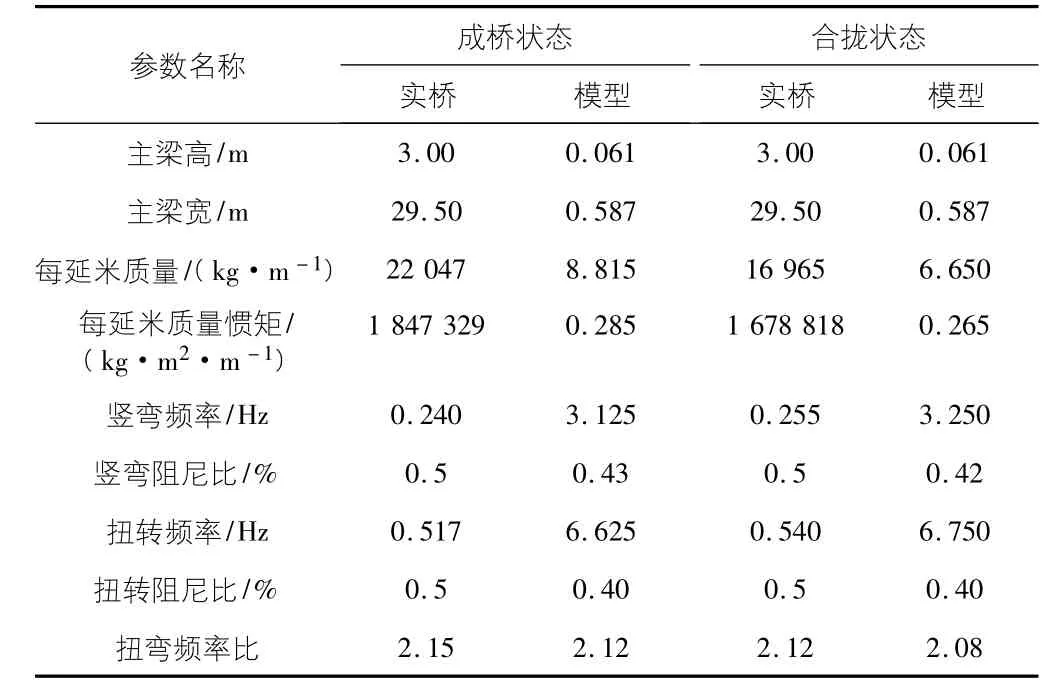
表3 振動力節段模型試驗參數

動力節段模型風洞試驗包含成橋狀態和施工階段。在均勻來流情況下，針對主梁斷面分別進行了五種風攻角(α為0°，±3°，±5°) 情況下的試驗。顫振臨界風速測試結果如表4 所示。可知: 無論是成橋狀態還是施工階段，在各試驗風攻角下，主梁的顫振臨界風速均大于顫振檢驗風速，證明結構安全。

6 主梁渦激振動性能試驗

當氣流繞過物體時會在物體兩側及尾流中產生周期性脫落的漩渦，并對物體產生上下交替的作用力。該周期性漩渦脫落的頻率與風速成正比，即隨著風速的變化，漩渦脫落的頻率也隨之變化，當漩渦脫落頻率與結構某階自振頻率相同時，會發生共振，這種振動被稱為渦激共振[6-8]。為研究該橋主梁渦激振動性能，考慮了大橋成橋狀態和100%施工狀態。渦激振動的試驗模型試驗參數與顫振略有不同，表5 列出部分試驗參數，其他參數同表4。

表4 節段模型得出的顫振臨界風速結果

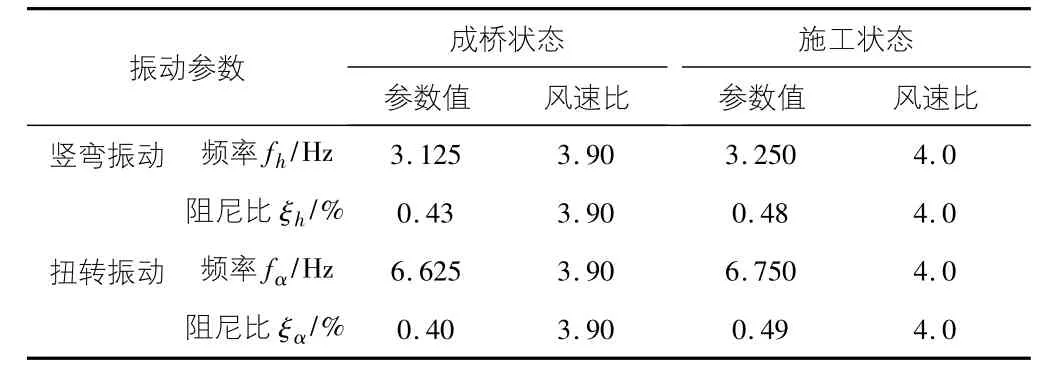
表5 渦振性能風洞試驗參數

節段模型試驗針對成橋狀態和施工狀態的主梁斷面，均分別進行了五種風攻角(0°，±3°，±5°) 條件下的渦激振動性能試驗。試驗在均勻流場中進行，風速范圍為1 m/s ～18 m/s。試驗起始，風速步長以0．5 m/s 取值進行遞增，找到其渦振區域后，再適當降低風速增加步長，繼而確定出渦激共振起始風速和最大振幅。

根據我國有關規范，紅河特大橋在成橋狀態時的一階對稱豎彎、扭轉渦振的振幅容許值分別為:

豎向:[ha]=0．04/fh=167 mm。

扭轉:[θa]=4．56/(fαB) =0．299°。

同樣，施工狀態時的渦振振幅容許值分別為:

豎向:[ha]=0．04/fh=157 mm。

扭轉:[θa]=4．56/fαB=0．286°。

試驗表明:該橋在施工狀態在所有試驗攻角下均沒有發生渦激振動現象。成橋態主梁在- 5°，- 3°，0°，+3°四種攻角情況下，沒有發現明顯的渦激振動。

在+5°風攻角下均有一個比較明顯的豎向渦激振動和扭轉渦激振動，豎向振動鎖定風速17．8 m/s，振幅為46 mm;扭轉鎖定風速為23．4 m/s，振幅為0．097°，豎向和扭轉振幅均沒有超出規范容許值，具體如圖4 所示。

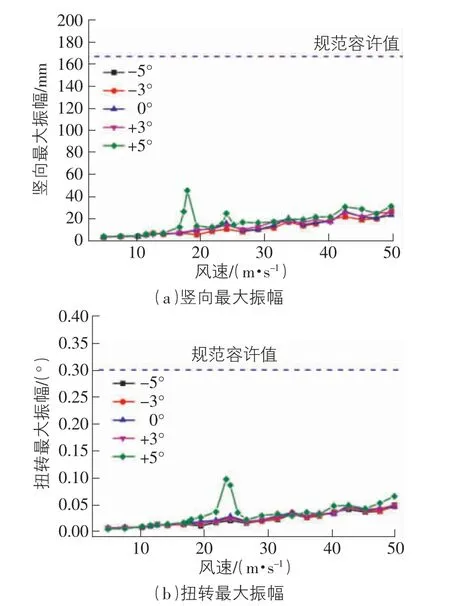
圖4 主梁成橋狀態渦振振幅

7 結論

1) 本橋鋼箱梁升力系數斜率為正，說明斷面具備氣動穩定的必要條件。主梁在0°攻角下阻力系數為0．64，從而表明流線箱型橋梁斷面具有較小的風荷載。2) 主梁設計成抗風性能較好的鋼箱梁，節段模型顫振穩定性試驗表明該橋成橋態及施工態在0°，+3°，-3°，+5°，-5°五種攻角下的顫振臨界風速大于橋梁結構的顫振檢驗風速，顫振安全性能夠保證。3) 由于本橋是流線型箱梁，施工狀態在所有試驗攻角下均沒有發生渦激振動現象。成橋態主梁在-5°，-3°，0°，+3°四種攻角情況下，均沒有發現明顯的渦激振動。在+5°風攻角下均有一個比較明顯的豎向渦激振動和扭轉渦激振動，豎向和扭轉渦振振幅均沒有超出規范容許值。