基于GASA-BRNN的齒槽轉矩預測方法與分析

任鴻昌，王東瑞，姜添惠，張闖，陳文輝

(沈陽工程學院 ，遼寧 沈陽 110136)

0 引言

在永磁同步電機(PMSM)轉動的過程中，由于電機齒槽與繞組分布不均勻，導致磁路不對稱，定子與轉子之間產生相對位移，使電樞齒槽與永磁體磁場間也產生相對位移，從而產生切向力，生成齒槽轉矩，使電機產生振動和噪聲，一定程度上降低其動態性能。目前國內外關于優化齒槽轉矩方面的研究主要以有限元法、解析法分析齒槽轉矩，對單一的結構參數進行優化，在離散的數據點中，尋找符合設計要求的值。此外還有部分學者，通過結合智能算法，構建多目標優化模型輔助電機設計，為多結構參數設計提出解決方案[1]。但是由于有限元法的計算時間長，解析法模型建立繁瑣，程序實現困難且不同結構變量需要建立不同的解析模型。因此針對實際電機設計中要求的多目標、多結構參數優化設計，上述方法難以應對這種復雜非線性問題，為設計者形成一種快速參考方案。

本文首先在Rmxprt中建立一款永磁同步電機模型，選擇3種結構參數為特征變量，齒槽轉矩為輸出，利用Ansys maxwell平臺對 PMSM 進行有限元仿真實驗，對選擇的3種特征變量進行參數化計算，得到360組實驗數據；然后設計一種基于GASA-BRNN神經網絡算法的齒槽轉矩分析模型，抽樣300組作為訓練輸入，將剩余數據和利用Ansys Workbench中響應面實驗(DOE)組件得到的13組數據混合作為測試數據，判斷模型的泛化能力。最后通過對GASA-BRNN模型的預測結果與有限元計算結果對比，并將其性能指標與不同改進策略的神經網絡模型進行分析，驗證其預測精度與實際適用性。

1 永磁同步電機模型與齒槽轉矩原理解析

1.1 電機有限元模型

本文將基于Rmxprt設計的一款4極24槽永磁同步電機作為典型研究案例，模型參數如表1所示。

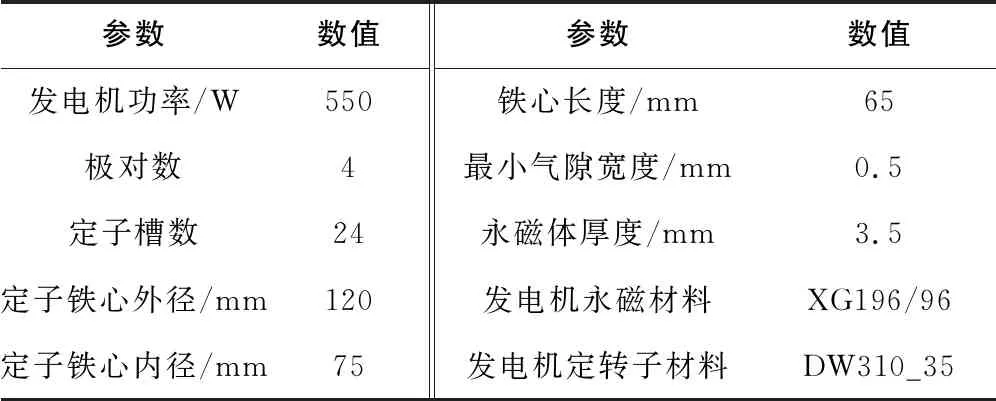
表1 樣機主要參數

通過在Ansys環境下Rmxprt與maxwell的快速對接，利用有限元仿真生成的PMSM二維模型如圖1所示。

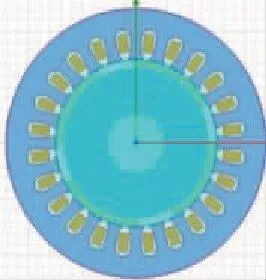
圖1 PMSM仿真結構

1.2 齒槽轉矩原理解析

空載運行下，定子和轉子產生相對位移，導致其間隙發生變化，即氣隙存在周期性變化，從而產生磁阻轉矩紋波即齒槽轉矩[2]，其可表現為斷電情況下電機內存儲的磁場能量對定子和轉子相對位置角的負導數。

(1)

式中α為定子齒與永磁體中心線的夾角。若不考慮磁場飽和,電機磁場儲存能量W可以近似看成電樞齒與永磁體之間氣隙g中的能量，W可近似表示為電樞齒與永磁體之間氣隙中的能量：

(2)

式中：μ0為空氣的磁導率；V為氣隙體積；B(θ,α)為磁感應強度，可近似表示為

(3)

式中：θ為永磁體沿圓周方向運動時與轉子軸之間的夾角；hm(θ)為永磁體磁極厚度；Br(θ)為永磁體剩磁；δ(θ,α)為永磁體有效氣隙長度沿圓周方向的分布系數。將式(3)帶入式(2)，得到電機磁場儲存能量：

(4)

假設發電機的每級磁通不變，令

(5)

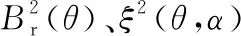
(6)

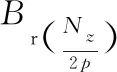
1.3 特征變量影響分析

在選擇特征變量的過程中，應當選擇對輸出目標的影響具有明顯特征的參數。本文選取極弧系數、永磁體偏心距、定子槽口寬度3種因子作為輸入量，選取周期內電機空載轉矩峰值為齒槽轉矩輸出量。通過有限元分析，分別計算在初始值條件下各變量與齒槽轉矩的單變量變化關系，如圖2-圖4所示。

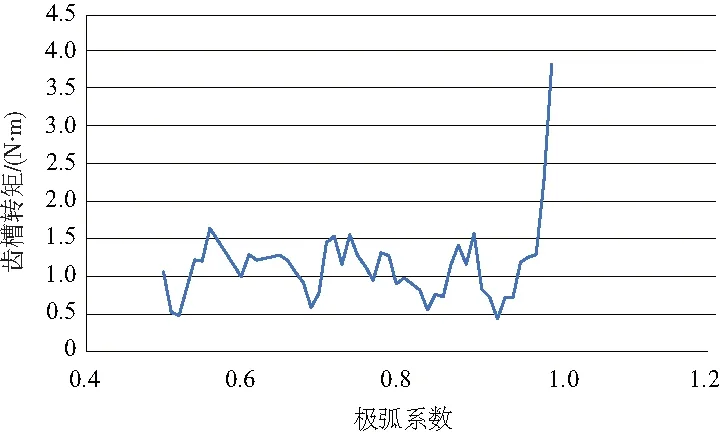
圖2 極弧系數與齒槽轉矩關系

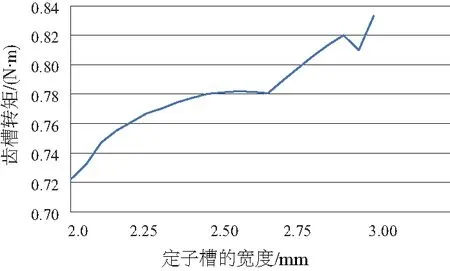
圖3 定子槽口寬度與齒槽轉矩關系

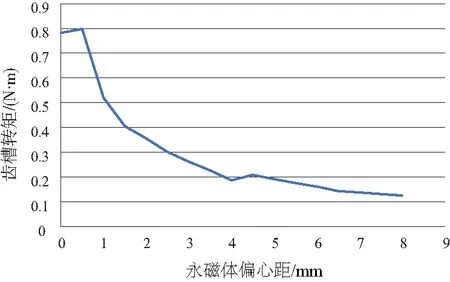
圖4 永磁體偏心距與齒槽轉矩關系

由有限元計算結果可知，在每種變量的變化范圍內，均對齒槽轉矩產生了明顯影響，且影響趨勢各不相同，變化曲線具有顯著的非線性關系。

2 BP神經網絡及其改進策略

2.1 BP神經網絡原理

BP網絡是一種典型的多層前饋型網絡，廣泛應用于模式識別、故障診斷，該模型結構如圖5所示。

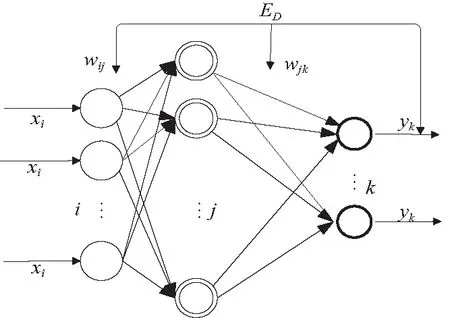
圖5 三層BP網絡結構

BP網絡一般由輸入層、隱藏層、輸出層組成。數據從輸入層依次傳播至隱藏層、輸出層，在輸出層將誤差反向傳播并調整網絡的權值參數，之后不斷迭代上述步驟至誤差為0，完成網絡的訓練過程。在誤差反向傳播過程中，令yk為第k個節點的實際輸出，tk為其期望輸出，誤差函數為

(7)

(8)

式中：i、j、k分別表示輸入層、隱藏層、輸出層的神經元；p為輸出變量數量；g(x)為激活函數；xi為輸入量。

由式(8)可知，誤差大小ED是權值wji、wkj的函數F(w)。因此通過調整權值來改變誤差，使得三層及以上的網絡結構能精準地描述出任意非線性關系，符合齒槽轉矩分析模型要求。

2.2 貝葉斯正則化神經網絡

標準BP神經網絡在迭代中很容易陷入局部最小，而初始權值的隨機確定導致每次擬合模型的精度差距過大，在針對復雜問題時的收斂速度過慢。目前廣泛使用的Matlab神經網絡工具箱默認的神經網絡訓練函數為Levenberg-Marquardt(L-M)算法，該算法多用于曲線擬合，在中小型網絡中廣泛應用，但是面對一個新輸入樣本具有很大依賴性。因此為提高齒槽轉矩預測精度，提高模型泛化性，本文使用貝葉斯正則化(bayesian regularization，BR)算法來對神經網絡進行改進。

神經網絡中的貝葉斯正則化算法是一個根據L-M優化來更新權值和偏置值的網絡訓練算法，通過貝葉斯定理將平方誤差和權重的組合最小化，確定正確的組合，從而產生一個泛化良好的網絡[3]。

在貝葉斯神經網絡中，定義網絡的權值為隨機變量，將網絡權值和訓練集的分布視為高斯分布，性能指數由式(8)轉化為

F(w)=αEw+βED

(9)

式中：Ew是網絡權重的平方和；指數參數α、β為貝葉斯網絡中的優化參數。BP神經網絡中尋得最小權值參數的目標函數是求式(8)的最小化，在BR神經網絡(BRNN)中，尋得最小權重空間則需要將式(9)最小化，相當于求相對應的后驗概率函數式(10)的最大化解集：

(10)

式中：w為權重分布；net為神經網絡結構。解得F(w)在最小點wmin時α、β結果如下：

(11)

式中：λ為有效參數，λ=p-2αtrace-1(H*)，反映了構成模型的規模，其中H是F(w)在最佳擬合直線或平面上的投影矩陣(海森矩陣)。求解之后進入L-M算法流程，在文獻[4]中有詳細推導，本文不再贅述。BRNN將不必要的權重趨近0，有效地消除了網絡的過擬合缺陷，同時使網絡具有快速收斂的特性。

2.3 遺傳算法

遺傳算法GA是一種全局優化算法，利用遺傳算法搜索BP神經網絡的初始權重可以保證獲得較高全局最優性的機會，因此，利用遺傳算法可以有效抑制神經網絡初始權值隨機化的缺陷。為強化遺傳算法的全局搜索能力，進一步降低算法陷入局部最優的可能性，本文將遺傳算法與模擬退火算法SA相結合，提出了GASA-BRNN算法，設計流程如下所述。

1)將神經網絡的權值和閾值編譯成實數組作為遺傳算法的染色體。初始化群體大小 30，交叉概率 0.3，變異概率 0.03，迭代次數50，退火溫度1 000。

2)計算種群中個體的適應度，加入退火因子拉伸標準適應度

(12)

式中：Fn為第n個個體適應度；k為當前個體迭代數；t為溫度。

3)按照遺傳策略，對代種群進行選擇操作、交叉操作和變異操作，形成下一代種群。結合 SA算法對產生的新種群采用Metropolis接受準則來確定，利用γn→m抽樣其中的新個體m。

Metropolis準則公式如下：

(13)

式中：Δ為新舊染色體的適應度之差；tk為控制參數。

4)設置接受概率，采用輪盤賭方法，N為染色體數量，接受概率公式如下：

(14)

5)判斷算法是否滿足停止準則，如果不滿足，則返回到2)；如果滿足，則輸出種群中最大適應度值的個體作為最優解，終止計算。

綜上所述，運用GASA改進BRNN算法可以有效避免由于初始權重的隨機確定而導致每次實驗得到的模型精度存在較大偏差，并進一步縮小了算法陷入局部最優的可能性，流程如圖6所示。

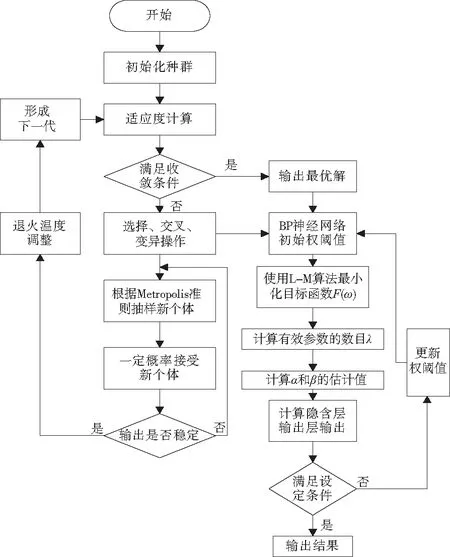
圖6 GASA-BRNN流程結構

3 性能計算與對比驗證

本文取極弧系數、定子槽寬度、永磁體偏心距作為特征變量，齒槽轉矩作為輸出，經全局計算得到輸入、輸出數據360組。為提高數據泛化能力通過中心化實驗得到13組數據特征與全局計算不同的數據，將其與全局計算中的60組數據合并作為訓練輸入，用以評估建立的GASA-BRNN模型的準確性與對新數據的擬合能力。特征變量選取范圍如表2所示。

表2 特征變量選取范圍

3.1 初始化參數與算法實現

本文采用Matlab2019實現算法，通過確定神經網絡層數與隱藏層節點數，選擇激活函數與訓練函數，添加學習率并給定網絡的目標誤差值，進行參數初始化調整，從而得到性能良好的網絡模型。

在神經網絡中輸入層神經元數目h由輸入數據的特征變量決定，輸出層神經元數目l由輸出變量決定，隱藏層神經元數目σ，一般選取經驗公式如下：

(15)

式中：ξ為[0,10]之間的常數；本文樣本空間中σ的取值范圍在[2,12]之間。但是σ與其余參數的確定一般具有很強的經驗規律，根據具體問題的表現也各不相同。因此通過選用均方誤差MSE與絕對值誤差MAE作為性能指標，對每次修改參數后的實驗模型進行精度評估。MSE計算公式與式(7)相同，MAE公式如下：

(16)

式中：p為輸出變量數，得到的值越小模型精度越高。多次實驗后得到相對合理的網絡參數配置如表3所示。

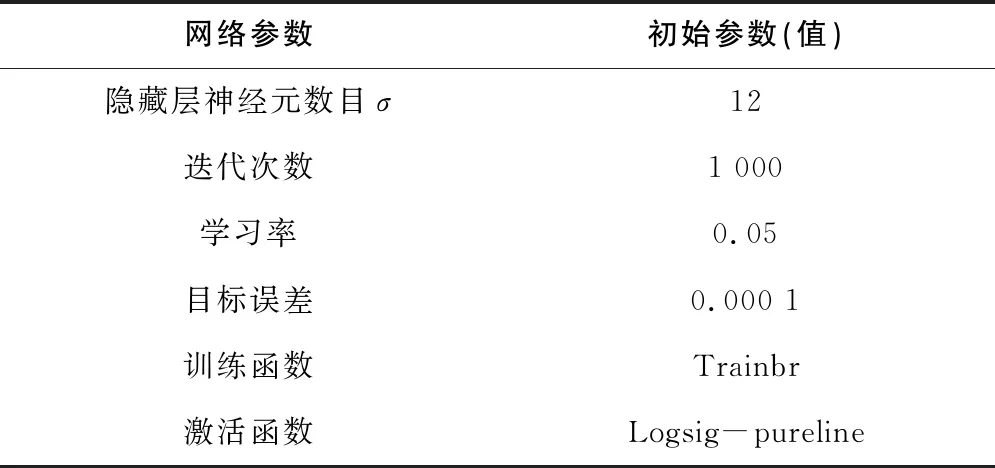
表3 網絡參數配置

3.2 性能計算

由于激活函數特性，網絡輸出值均在[0,1]之間，同時由于有限元直接得到的數據具有一定序列特征，因此將數據導入模型前，需要對劃分后的數據集進行歸一化處理并進行隨機排序再進行導入。在訓練過程中，GASA算法調節適應度過程如圖7所示。

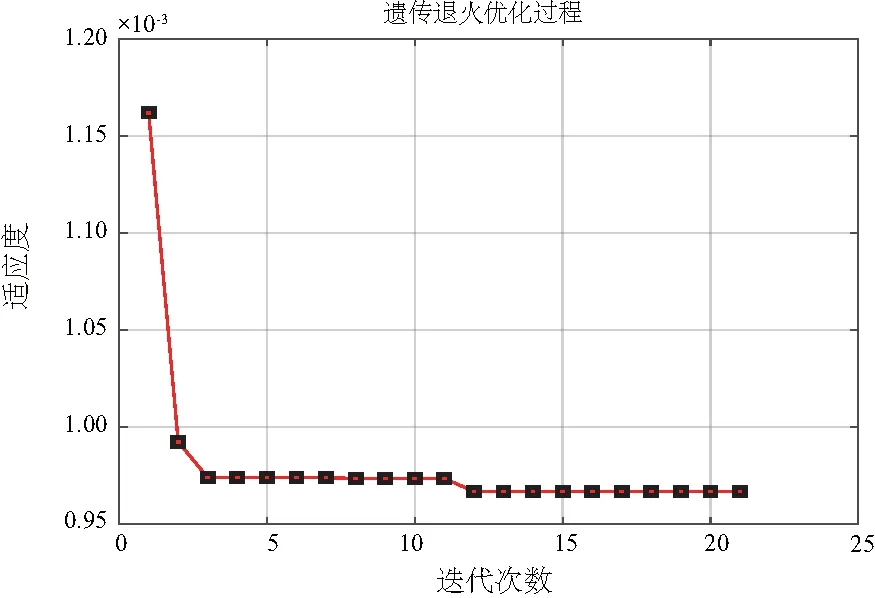
圖7 適應度調節過程

為直觀顯示GASA-BRNN模型在齒槽轉矩預測方面的優越性，同時驗證其在分析齒槽轉矩中的可靠性，將模型得到的測試集數據與傳統BP神經網絡得到的測試集數據對有限元輸出的實際值進行比較，可視化結果如圖8-圖9所示。

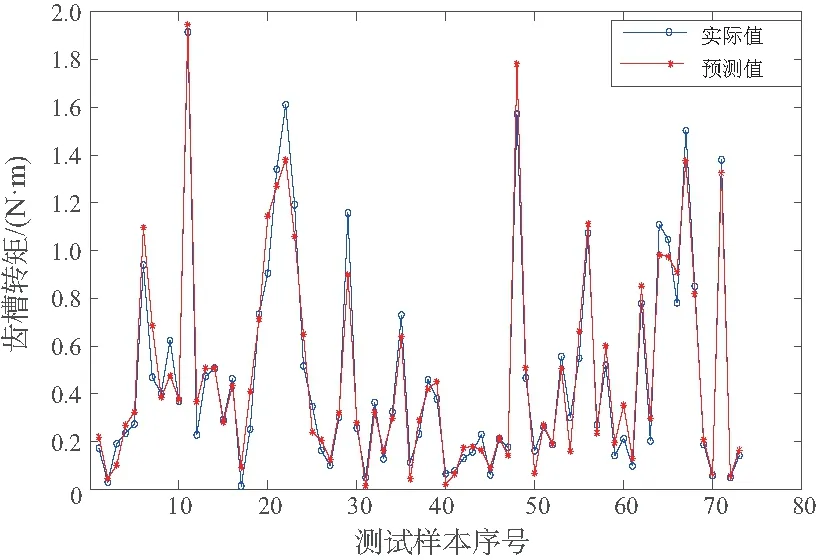
圖8 BP神經網絡預測結果

由圖8-圖9可以看出，本文提出的GASA-BRNN模型相比于標準BP神經網絡具有更好的預測性能，對比有

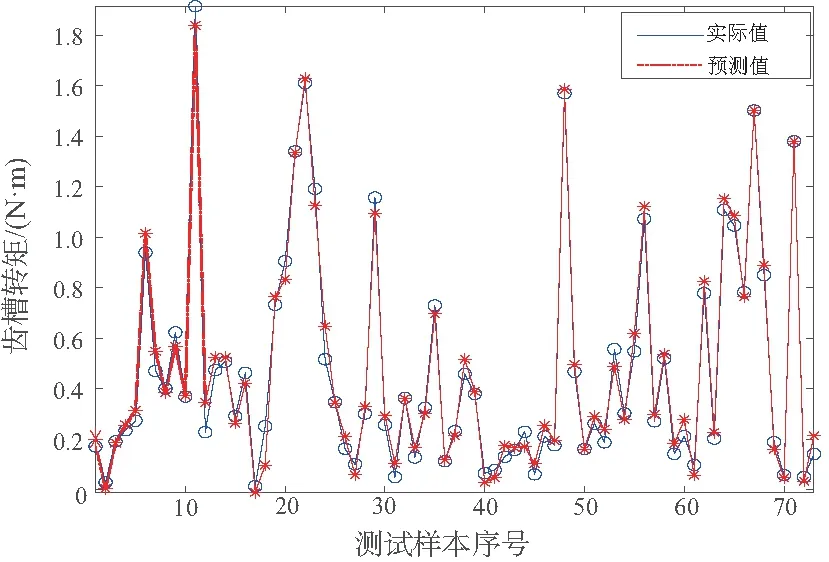
圖9 GASA-BRNN預測結果

限元方法得到的實際輸出齒槽轉矩曲線，GASA-BRNN模型具有令人滿意的擬合程度。為進一步證明本文提出的模型在分析齒槽轉矩方面的優秀性能，額外選取GA-BP、PSO-BP、RBF 3種神經網絡模型，在訓練調整各自最優初始值后，對測試數據的性能表現如表4所示。

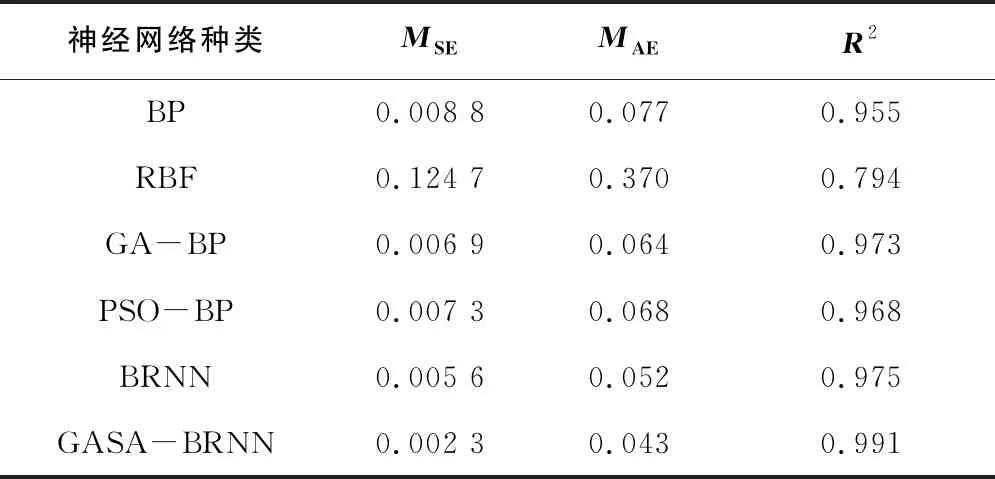
表4 性能表現

表4中R2為數據擬合的關聯度，由性能參數可知，雖然各改進算法相對于標準BP各有提升，但是本文提出的以極弧系數、永磁體偏心距、定子槽口寬度為輸入，齒槽轉矩為輸出的GASA-BRNN算法模型具有更加優秀的性能。

4 結語

本文將神經網絡算法應用于永磁同步電機齒槽轉矩的預測中，并根據BP神經網絡的缺陷結合遺傳算法與模擬退火算法進行改進，利用貝葉斯正則化訓練算法提高了模型的泛化能力。在樣本上則選擇了三輸入、單輸出的PMSM小樣本有限元仿真案例，通過數據處理反復進行性能分析實驗，設計出良好的建模策略，完成了GASA-BRNN模型建立和對比分析，相對于文獻[5]提出的深度學習模型， GASA-BRNN模型簡化了實現過程，且根據各類性能指標以及與有限元計算結果的對比，顯示其具有很高的預測精度，為電機結構實現快速設計奠定基礎。