基于梯度提升決策樹分位數回歸的船舶能耗區間預測

李天笑　 周田瑞　胡勤友　 郝清晏

摘要：針對目前船舶能耗預測方法僅僅能進行單點預測的問題，提出一種梯度提升決策樹分位數回歸方法對船舶能耗區間進行預測。對船舶能耗及其影響因素數據進行預處理（空值、異常值刪除等），獲得更加準確的船舶能耗數據集。結合相關領域知識，確定對地航速、艏艉吃水、左右吃水、風速等9個影響因素進行建模。以區間覆蓋率和平均帶寬作為該方法的性能評價指標。實驗結果表明，該方法能有效獲取船舶能耗區間值，與分位數回歸森林（quantile regression forest，QRF）、普通線性分位數回歸（quantile regression， QR）相比，其預測性能更佳。提出的方法可為智能船舶能耗狀態實時監測、異常識別等提供參考。

關鍵詞：? 船舶能耗; 區間預測; 梯度提升決策樹; 分位數回歸

中圖分類號：? U676.3文獻標志碼：? A

Ship energy consumption interval prediction based on gradient

boosting decision tree quantile regression

Abstract： Aiming at the problem that the current ship energy consumption prediction methods can only make a single point prediction， a gradient boosting decision tree quantile regression method is proposed to predict the interval of ship energy consumption. The data of the ship energy consumption and its influence factors are preprocessed to obtain a more accurate data set of ship energy efficiency （null， outlier deletion， etc.）. Combined with the knowledge of relevant fields， 9 influence factors are determined for modeling， such as the speed over ground， the fore and aft draft， the left and right draft， and the wind speed. The interval coverage and the mean bandwidth are used as performance evaluation indices of the proposed method. The experimental results show that， the proposed method can effectively obtain the ship energy consumption interval values， and have better prediction performance compared with the quantile regression forest （QRF） and the ordinary linear quantile regression （QR）. The proposed method can provide reference for realtime monitoring of energy consumption status and abnormal identification of intelligent ships.

Key words： ship energy consumption; interval prediction; gradient boosting decision tree; quantile regression

引言

船舶是全球貿易商品不可或缺的運輸工具，承擔了全球80%貨物的運輸，但巨大的運輸量也帶來了眾多的環境問題[1]。根據國際海事組織2014年發布的溫室氣體報告，2007—2012年全球航運業每年的二氧化碳排放量為1 015萬t。若不采取相關控制措施，到2050年二氧化碳排放總量將比2012年提高50%～250%。為達到節能減排的目的，國際海事組織采取了一系列相關措施，如要求新船能夠滿足船舶能效設計指數（energy efficiency design index， EEDI）[2]，并強制實施船舶能效管理計劃（ship energy efficiency management plan，SEEMP），利用船舶能效營運指數（energy efficiency operational indicator，EEOI）評判船舶的營運能效水平。

目前船舶能耗模型的建立主要有3種方法：（1）基于經驗公式，將船舶阻力劃分為靜水阻力和風浪引起的附加阻力，建立主機與螺旋槳之間的能量傳遞關系。（2）利用計算流體力學（computational fluid dynamics， CFD）或MATLAB等仿真軟件模擬船舶不同狀態，進而獲得不同航速與阻力之間的關系，并在此基礎上獲得航速與單位時間主機油耗（即船舶能耗）的函數關系。（3）基于機器學習，根據船舶的航行數據、主機燃油數據等，通過求取各個影響因素與能耗的相關系數大小確定影響能耗的主要因素，利用人工神經網絡、支持向量機、隨機森林（random forest，RF）等機器學習算法建立船舶能耗模型。HOLTROP[3]通過將船舶阻力劃分為若干個相加的成分，利用船模實驗獲得不同航速下船舶阻力情況，并結合大量的實船數據最終獲得了功率與航速的回歸模型。LEIFSSON等[4]考慮風阻、船舶主機、螺旋槳的工作性能，結合經驗公式建立主機油耗灰箱模型，獲得經驗公式的最佳參數值，并利用神經網絡對其預測結果進行校正。張偉等[5]基于船舶主機與螺旋槳之間的能量傳遞關系并結合理論公式建立了航速與船舶能耗之間的數學關系。SALA等[6]使用可調螺旋槳，通過調整螺距建立了主機轉速與船舶能耗的關系。范愛龍等[7]和孫星等[8]考慮通航環境的影響，利用MATLAB/Simulink建立內河主機能耗模型。PARKES等[9]基于3艘大型姐妹商船的航行數據，建立了基于反向傳播（back propagation，BP）神經網絡的能耗預測模型，通過求取各個影響因素與主機油耗的斯皮爾曼等級相關系數，確定輸入變量，結果顯示這個模型的預測精度高于線性回歸模型的預測精度。BUIDUY等[10]基于集裝箱實時傳感器數據，提出一種基于深度學習的船舶能耗預測模型，結果顯示，在考慮載重噸、風速、風向等影響因素后，模型的預測精度得到提高。WANG等[11]針對主機油耗影響因素較多，且部分影響因素之間存在一定的相關性，提出了一種基于最小絕對收縮選擇算子（least absolute shrinkage and selection operator， LASSO）的能耗回歸模型。1074B629-AF89-4C87-B546-7BAB15150F23

目前的船舶能耗預測主要是基于傳感器數據、午時報告數據等，先采用特征工程或結合領域知識確定影響能耗的主要因素，然后使用人工神經網絡、支持向量機、LASSO等機器學習算法獲得不同輸入變量與能耗的映射關系。通過這種預測主要獲取的是點與點之間的映射關系，然而在確定船舶能耗影響因素時不可能考慮到所有的因素，因此考慮重要因素影響的船舶能耗預測值并不能反映其他非重要因素對能耗的影響，故提出通過能耗區間預測來反映未被考慮因素對能耗的影響。一方面能耗區間預測保留了船舶能耗的波動性，為各種未被考慮的影響因素預留空間;另一方面，區間預測有利于識別船舶能耗異常值，方便對其動態分布進行分析。本研究通過在船上安裝各種傳感器，采集相關能耗數據，并對采集的數據進行預處理，建立能耗數據集，結合分位數回歸（quantile regression， QR）與梯度提升決策樹（gradient boosting decision tree，GBDT），最終建立基于GBDTQR的船舶能耗區間預測模型。

1船舶能耗數據采集及預處理

1.1數據采集

在某一貨船上安裝傳感器（如AIS、GPS、油耗監測儀等）采集數據。采集時間為2018年3月2日至4月19日 ，采集的數據包括船舶經緯度、對地航速、對水航速、艏艉向、艏吃水、艉吃水、左吃水、右吃水風速、風向、流速、流向、主機油耗等。

1.2數據預處理

在數據采集過程中由于設備損壞、傳輸過程信號較差等，數據會發生錯誤、缺失等，從而數據質量受到影響。若將含有噪聲的數據直接用于模型訓練，訓練結果并不能反映潛在的知識規律。本文根據船舶能耗區間預測需要，基于已有文獻，最終提取對地航速、艏吃水、艉吃水、左吃水、右吃水、風速、風向、流速、流向共9個影響因素，每個樣本數據均由這9個影響因素數據與主機油耗數據構成。對這些數據進行預處理：（1）該船為遠洋船，其航速處于一定范圍內，根據其歷史航速數據，該船航速大部分處于[4， 16]kn范圍內，將航速不在此范圍內的樣本刪除。（2）該船吃水在[9， 15]m范圍內，將吃水不在此范圍內的樣本刪除。（3）將流向、風向不在[0°，360°]范圍內的樣本刪除。（4）將主機油耗小于0的樣本刪除。經過數據預處理后，數據樣本從12 975個減少至12 729個。

1'3數據轉化

由于采集主機油耗數據的時間間隔是5 min，為方便研究，將其換算成每日油耗量：（1）式中：M為主機5 min的油耗量。

采集的風向、流向數據為絕對風向、流向數據，而風向、流向對船舶能耗影響的研究是建立在相對風向、流向的基礎上的，故需將絕對風向、流向數據換算成相對風向、流向數據：

（2）

（3）

式中：θRW為相對風向;θW為絕對風向;θS為船艏向;θRC為相對流向;θC為絕對流向。絕對風向和絕對流向都以真北方向作為衡量標準，順時針方向為正。

2模型建立

21GBDT原理

GBDT是基于集成學習Boosting方式建立的[12]。它要經過多次迭代并構建多個決策樹來組成集成模型。在每次迭代過程中，各決策樹學習器沿著梯度下降最快的方向降低殘差。該算法因具有解釋性強、預測速度快、預測時能自由組合多個影響因素等優點[13]而被廣泛應用。

在構建模型時，各決策樹之間具有很強的關聯性，下棵決策樹根據上棵決策樹的訓練結果不斷調整自身權重，依次不斷迭代，直到達到期望殘差或設定的最大迭代次數。GBDT預測過程見圖1。

預測模型為（4）式中：F（x）為輸入變量x的響應值;ωk和φk分別為第k棵決策樹的權重和參數;g（x，φk）為第k棵決策樹的預測值。

基于樣本數據（xi，yi），通過下式求得ωk和φk的最優值：

（5）

式中：yi為因變量;FK-1（xi）為經K-1輪迭代后得到的預測結果。

22基于GBDTQR的船舶能耗模型

QR用于估計自變量對不同分布的因變量產生的不同影響。假設因變量yi受到m個自變量xi，1，xi，2，…，xi，m的影響，則QR模型可表示為

（6）

式中：α0（τ）為誤差項;系數α1（τ），α2（τ），…，αm（τ）可通過式（8）求得，其值隨著τ的變化而變化，τ∈[0，1]。

（7）

式中：xi=（xi，1，xi，2，…，xi，m），α=（α1（τ），α2（τ），…，αm（τ））T。若u<0，則損失函數ρτ（u）=u（τ-1）;若u≥0，則ρτ（u）=uτ。

由式（6）可知，QR是一種線性回歸，然而船舶能耗與各影響因素之間的關系并不是簡單的線性關系，因此結合GBDT提出一種GBDTQR方法，其各參數估計值可通過式（8）求得：

（8）

將k（τ）和k（τ）代入式（4）即可得到yi的τ分位數估計值。

不同概率的預測區間可通過設置不同的置信水平獲取。若置信水平為1-β，則它的上分位點為1-β/2，對應的預測值為U1-β/2i;下分位點為β/2，對應的預測值為Lβ/2i;預測區間為[Lβ/2i，U1-β/2i]。GBDTQR方法的運算過程見圖2。

3算例分析

3.1實驗條件

本文所涉及實驗均是在Window 10、64位操作系統、8 GB內存、Inter Core i5處理器、基于Spyder的集成開發環境Python 37或MATLAB 下完成的。其GBDT調用ScikitGarden庫，其參數見表1，沒有涉及的參數一律采用庫中默認值。

3.2不同預測方法對船舶能耗的單值預測1074B629-AF89-4C87-B546-7BAB15150F23

先比較GBDT和RF對船舶能耗的單值預測，以90%的數據作為訓練集，剩下的10%的數據作為測試集。由圖3可以看出，RF和GBDT對船舶能耗的預測值都能較好地契合船舶能耗實際值，而RF在對船舶能耗的局部極值進行預測時過度擬合情況出現的頻率是明顯高于GBDT的。GBDT的均方誤差為317，小于RF的均方誤差（595）;GBDT的運算時間要遠遠小于RF的：這說明GBDT比RF的性能優。

3.3不同置信水平下的預測結果分析

為研究不同置信水平下的船舶能耗區間，將置信水平分別設置為95%、90%、85%、80%。以90%的數據作為訓練集，剩余的10%的數據作為測試集。各置信水平下的船舶能耗區間預測結果見圖4，由于測試樣本數量較多，僅選取200個樣本進行展示。

圖4顯示了測試樣本的船舶能耗預測區間上下限和實際值。從圖4可知：大部分實際值均能落在預測區間內，且預測區間上下限整體變化趨勢與實際值保持一致;當實際值較大或較小時，其預測區間并不能很精準地覆蓋實際值，這是因為這些實際值本身存在誤差或其數據集中與其相似的樣本較少，從而導致預測區間上下限波動較大;對于波動較小的實際值，其預測區間基本能覆蓋大量的實際值，且隨著置信水平的增加，預測區間上下限波動范圍減小。

3.4不同方法性能對比

為驗證本文提出的GBDTQR方法的優越性，將其與分位數回歸森林（quantile regression forest，QRF）、普通線性分位數回歸（QR）進行對比。為評估所提出方法的優劣，將區間覆蓋率（BP）和相對帶寬（BW）作為性能評價指標：（9）

（10）

式中：T為樣本量;U1-β/2i和Lβ/2i分別為β置信水平下預測區間的上限和下限。

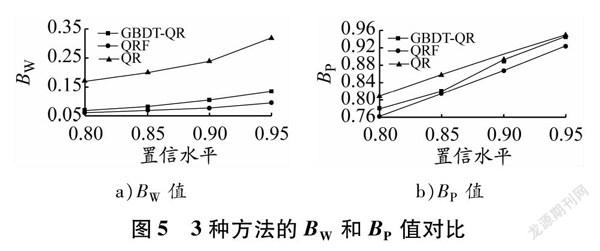
（11）由式（9）～（11）可知，當BP相同時，BW越小表明該方法預測性能越好;當BW相同時，BP越大表明該方法預測性能越好。3種方法的BP和BW值見表2。從表2可知：比較 BP值，QR的最高，GBDTQR的次之，QRF的最小，這是因為船舶能耗與航速具有高度相關性，且速度相對集中，變化范圍較小，通過QR能相對準確地獲得各個輸入變量與船舶能耗的映射關系;比較BW值，QRF的最小，GBDTQR的次之，QR的最大;GBDTQR與QR的BP值在不同置信水平下相差不大，但這2種方法的BW值相差較大。為更加直觀地比較不同方法的預測性能，將3種方法的BP、BW值繪制成折線圖，見圖5。

從圖5可知，3種方法的BP和BW值均隨置信

水平的增加而增加，這是因為提高BP值必然是以犧牲BW為代價的。然而，各個方法BP和BW的提高幅度并不一致，GBDTQR的BP值提高幅度最大;QR的BW值提高幅度最大，且在同一置信水平下，GBDTQR與QRF的BW值相差不大。通過對比發現，當置信水平為95%時，GBDTQR與QR的BP值相差不大，但BW值卻相差較大，QR的BW值約是GBDTQR的兩倍。對比GBDTQR與QRF兩種方法：在同一置信水平下，兩種方法的BP的差值大于BW的差值，且這兩種方法的BW值都比較小;當置信水平為95%時，兩種方法的BW值均低于015，而此時兩者的BW值竟相差02。因此，當設置置信區間為95%時，綜合分析BP和BW值得出，提出的GBDTQR優于QRF和QR。

4結論

本文提出一種梯度提升決策樹分位數回歸方法（GBDTQR）對船舶能耗區間進行預測。通過多源傳感器采集船舶能耗及其影響因素數據，并對采集到的數據進行空值、異常值刪除等預處理，建立船舶能耗數據庫。提取主機油耗、對地航速、艏吃水、艉吃水、風速、風向、流速、流向等10類數據進行建模。在80%、85%、90%和95%置信水平下對船舶能耗區間進行預測，結果顯示大部分船舶能耗實際值均能落在預測區間內，整體上預測區間比較穩定，驗證了模型的有效性，并且隨著置信水平的增加，落入預測區間的樣本數增加。為評估該方法的優劣，使用區間覆蓋率（BP）和平均帶寬（BW）作為評價指標，并與分位數回歸森林（QRF）、普通線性分位數回歸（QR）進行對比。在95%置信水平下，GBDTQR與QR的BP值差別不大，QRF的BP值最小，但QR的BW值是GBDTQR的兩倍，因此GBDTQR優于QRF和QR。本文僅對船舶能耗區間進行了預測，并未對船舶能耗異常值進行識別。未來將利用GBDTQR進行在航船舶能耗實時監測和船舶能耗異常值識別，為智能船舶能耗管理及優化提供指導。

參考文獻：

[1]Marine Environment Protection Committee. Prevention of airpollution from ships （Second IMO GHG Study 2009）[R]. London： International Maritime Organization， 2009.

[2]Marine Environment Protection Committee. Prevention of airpollutionfrom ships （Third IMO GHG Study 2014）[R].London： International Maritime Organization， 2014.

[3]HOLTROP J. A statistical reanalysis of resistance and propulsion data[J]. International Ship Building Progress， 1984， 31： 272276.

[4]LEIFSSON I ， SVARSTTIR H， SIGURDSSON S ， et al. Greybox modeling of an ocean vessel for operational optimization[J]. Simulation Modelling Practice and Theory， 2008， 16（8）： 923932. DOI： 101016/j.simpat.200803006.1074B629-AF89-4C87-B546-7BAB15150F23

[5]張偉， 王紅， 張澍寧， 等. 內河船舶主機動態油耗模型的研究與建立[J]. 交通標準化， 2013（22）： 9597. DOI： 1016503/J.CNKI.20959931201322041.

[6]SALA A， DE CARLO F，BUGLIONI G， et al. Energy performance evaluation of fishing vessels by fuel mass flow measuring system[J]. Ocean Engineering， 2011， 38（5/6）： 804809. DOI： 101016/j.oceaneng.201102004.

[7]范愛龍， 嚴新平， 尹奇志， 等. 船舶主機能效模型[J]. 交通運輸工程學報， 2015， 15（4）： 6976. DOI： 1019818/j.cnki.16711637201504009.

[8]孫星， 嚴新平， 尹奇志， 等. 考慮通航環境要素的內河船舶主機營運能效模型[J]. 武漢理工大學學報（交通科學與工程版）， 2015， 39（2）： 264267. DOI： 103963/j.issn.20953844201502008.

[9]PARKES A I， SOBEY A J， HUDSON D A. Physicsbased shaft power prediction for large merchant ships using neural networks[J]. Ocean Engineering， 2018， 166： 92104. DOI： 101016/j.oceaneng.201807060.

[10]BUIDUY L， VUTHIMINH N. Utilization of a deep learningbased fuel consumption model in choosing a liner shipping route for container ships in Asia[J].The Asian Journal of Shipping and Logistics， 2020， 37（1）： 111. DOI： 101016/j.ajsl.202004003.

[11]WANG S Z， JI B X， ZHAO J S， et al. Predicting ship fuel consumption based on LASSO regression[J]. Transportation Research Part D： Transport and Environment， 2018， 65： 817824. DOI： 101016/j.trd.201709014.

[12]王慧君， 胡定玉， 方宇， 等. 基于梯度提升決策樹的車輪輪緣厚度磨耗預測[J]. 測控技術， 2020， 39（11）： 8084. DOI： 1019708/j.ckjs.202011015.

[13]楊錫運， 邢國通， 馬雪， 等. 一種核極限學習機分位數回歸模型及風電功率區間預測[J]. 太陽能學報， 2020， 41（11）： 300306.

（編輯趙勉）

收稿日期： 20210307修回日期： 20210906

基金項目： 上海市科學技術委員會重大項目（18DZ1206300）

作者簡介： 李天笑（1995—），女，江蘇揚州人，碩士研究生，研究方向為海上交通系統的優化方法與智能化，（Email）598018282@qq.com;

周田瑞（1991—），男，江西吉安人，博士研究生，研究方向為船舶能效提升，（Email）1241514977@qq.com;

胡勤友（1974—），男，安徽舒城人，教授，博士，研究方向為智能船舶與海事信息處理，（ Email）qyhu@shmtu.edu.cn1074B629-AF89-4C87-B546-7BAB15150F23