支持學生數學問題提出的教學策略

江蘇省蘇州市吳江區鱸鄉實驗小學 李 新

數學問題提出是指學生在已有數學經驗的基礎上，對具體的情境給出自己的理解，并建構有意義的數學問題。新課標強調通過義務教育階段的學習，學生能“初步學會從數學的角度發現并提出問題”。正如愛因斯坦所說的“提出一個問題往往比解決一個問題更重要”，問題提出對于數學教學的重要性也是不言而喻的，蔡金法教授認為“問題提出是一個教學目標、一種認知活動、一種教學手段”，而且“如果一定要我挑出一個最主要的研究問題，那就是數學問題提出的課堂教學研究”。從教學目標的角度講，與分析、解決問題的能力一樣，學生發現和提出問題的能力也需要教師在教學中有目的、有意識、有計劃、有步驟地加以培養；從認知活動的角度講，問題提出能促進學生的思維發展，激發學生的好奇心、成就感，使學生產生積極的情感體驗，提高參與學習活動的積極性；從教學手段的角度講，問題提出能促進學生理解數學概念、探索數學規律、解決數學問題，實現高層次的教學目標。支持學生數學問題提出的教學策略，旨在通過教學，充分激活學生已有的數學經驗，提供豐富的課程資源，創設有效的數學情境，促進學生主動建構有意義的數學問題。

一、基于問題解決引導學生提出問題

如果把問題解決看成一個周期，問題提出就是問題解決的開始，而一個問題的解決又預示著一個新問題的開始，甚至往往在問題解決的過程中，問題解決者（這里主要指學生）也會提出問題，或者指向并促進原來問題的解決，或者孕育新的問題。從這個意義上講，問題提出與問題解決是相互促進、協同前行的。

（一）引問：提出初始問題

引問，有兩層含義，一是引導學生提出問題；二是使學生在問題的引領下展開積極的思維活動。為引導學生提出問題，教師要注重情境的創設。指向問題提出的情境創設，既要激發學生產生把所提出的也是要解決的問題和已有經驗之間聯系起來的興趣，也要切實幫助學生能夠在所提出的也是要解決的問題和已有知識結構之間建立實質性的聯系。為使問題能引領學生積極思考，教師要注重讓學生理解問題，具體來講就是使學生理解已知和未知之間的距離，并能直覺地體悟由已知到未知應經由怎樣的路徑、采取何種可能的策略。

比如，教學“平行四邊形的面積”時，教師可以這樣引問：教師出示木條制作的長方形框架，告知學生其長7分米、寬5分米，讓學生提出問題。學生會問“周長是多少、面積是多少”并解決。接著，教師演示，將長方形框架“壓扁”成平行四邊形，“壓扁”的過程是動態的、連續的，從中選取兩個平行四邊形呈現出來（如圖1），再讓學生提問，學生仍問“平行四邊形的周長是多少、面積是多少”。求周長容易解決，而且，周長不變；求面積時則出現爭議，有學生認為其面積和長方形的相同，也就是7×5=35平方分米；有學生認為其周長比長方形的小，而且兩個平行四邊形的面積也不同。于是，問題產生了：這兩個平行四邊形的面積到底是多少平方分米？

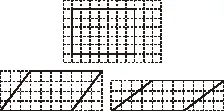
圖1

（二）追問：提出深度問題

追問，是教師激發、啟發學生深入、持續思考常用的教學策略。指向問題提出的教學，應努力提供機會（比如時間、空間以及必要的啟發、引導），促進學生在問題解決過程中展開追問。從追問的主體看，可以是學生自我追問、相互追問；從追問的目的看，可以是有疑而問（即在問題解決過程中，確有疑惑，想要問老師或同學），也可以是為證而問（即在問題解決過程中，自己有所思考、有所心得，想向老師或同學求證，想聽聽他們是否有同樣的想法）；從追問的作用看，可以是促進對具體問題的更深入理解，也可以是推動具體問題向一般化、抽象化方向發展。

還是以“平行四邊形的面積”的教學為例。在“引問”階段提出了具體問題“這兩個平行四邊形面積各是多少”，學生運用已有的知識經驗（主要是對面積意義的理解、對數方格求面積方法的掌握、對圖形通過“剪、移、拼”轉化后面積不變原理的直覺感悟等），借助工具和材料（剪刀、畫在方格紙上的平行四邊形等）解決了這兩個具體問題，也證實在“壓扁”的過程中平行四邊形面積要比原來長方形的面積更小。教師讓學生思考：“能想到什么新的問題？”經過獨立思考、小組討論，學生提出“四條邊長度沒有變，為什么這樣得到的平行四邊形面積比要原來長方形的小”“平行四邊形的面積和什么有關”“如果任意給出一個平行四邊形，面積怎樣求 ”等問題。

（三）續問：提出后繼問題

續問，是解決“引問”“追問”環節所提出的問題后，學生反思解決這些問題的過程，提煉所能獲得的知識、技能，所感悟的思想、經驗，通過舉一反三、以此類推等策略，提出可以繼續研究的問題。

仍以“平行四邊形的面積”的教學為例。在本堂課快要結束的時候，教師引導學生回顧本課是如何研究“平行四邊形的面積”的，并選取一些關鍵活動場景再次呈現出來（展示當時的PPT并配合語言講解、師生互動），強化其中“研究了什么問題”“是怎樣提出這些問題的”“是怎樣解決這些問題的”“通過解決問題得到什么結論”等關鍵信息，之后問大家：“關于今天的學習，大家還有什么問題？”“受今天學習的啟發，接下來大家想研究什么問題？” 經過獨立思考、小組討論，學生提出：“長方形壓扁變成平行四邊形，面積變小，跟角度變小了有沒有關系？”“我想研究三角形的面積怎么求、梯形的面積怎么求。”

需要指出的是，無論引問、追問、續問，還是其他激發提問的策略，都需要教師發揮主導作用，比如，給學生創設提問的情境、搭建提問“支架”，可以運用材料或工具、發揮語言的作用，采用疑問、設問、反問甚至暗示、提醒等策略，引導學生提出有價值的問題。長期堅持，能幫助學生形成提問的習慣。

二、指向數學理解啟發學生提出問題

數學學習強調理解已經成為廣大教師的共識。英國數學教育家斯根普將理解分為工具性理解和關系性理解。工具性理解是表面的、外部的、形式上的理解，它解決是什么、做什么、怎么做；關系性理解涉及事物內部結構意義等的理解，反映事物內在的本質規律，解決為什么，以及活動的有效性、合理性。從教學實踐看，學生在認識、理解數學的初期，往往是工具性理解，再逐步走向關系性理解。啟發學生提出問題，既能提高學生工具性理解的有效性，也能促進其向關系性理解轉變。

（一）促進發現：提出優化工具性理解的問題

傳統教學中，對工具性理解的定位較為機械，采用“概念（定義、定理）—實例—練習（習題）”的教學模式，使學生學習基礎知識、基本技能時過于依賴模仿、記憶、操練。但是，“就對概念或法則的學習過程而言，工具性理解應當是其中一個重要的甚至是不可缺少的環節”。雖然工具性理解指向“是什么、做什么、怎么做”，但是這些知識（包括數學的陳述性知識、程序性知識）的獲得，可以采用發現的方式進行，使工具性理解得以優化，而問題提出恰好是發現的起點。

比如，教學“3的倍數的特征”時，從工具性理解的角度看，學生的學習任務是知道“3的倍數的特征”是什么，以及“3的倍數的特征”怎么用（如通過計算2+8+3+2=15，判斷2832是3的倍數）。為促進學生主動發現這些知識，教師可以這樣啟發學生提問：首先讓學生運用類比、發揮“學習2、5的倍數的特征時所用方法”的定式作用，提出“3的倍數的特征也看個位”的猜想，并從百數表中圈出3的倍數，發現猜想錯誤，進而提出“3的倍數的特征看什么”的問題；接著，在教師的引導下，學生通過“在計數器上用珠子表示3的倍數”（數感強的學生，不借助計數器而直接看這些數就能有所發現），初步發現“百數表中的3的倍數，各位上數的和是3的倍數”，此時，教師說：“100以內，3的倍數，各位上數的和都是3的倍數。這個發現，能否就作為3的倍數的特征？”教師說這句話時，“100以內”“3的倍數”交替讀重音，并配合身體語言進行啟發乃至暗示，讓學生提出問題“100以上的3的倍數，各位上數的和是否是3的倍數？”“不是3的倍數，各位上數的和會是3的倍數嗎？”在這兩個問題的引領下，學生繼續開啟發現之旅，并最終獲得結論。

（二）深入探究：提出實現關系性理解的問題

就數學知識的學習而言，斯根普明確指出更多的理解應當定位于“關系性理解”，即最終我們應當讓學生獲得的是關系性理解。如何促進工具性理解向關系性理解轉化？一是要使學生理解與把握數學對象的本質屬性、典型實例及相互關系；二是使學生能將所學知識自覺與已有的知識經驗相聯系，完善和改組認知結構；三是讓學生在問題解決過程中，培養知識的遷移能力，通過反思提高元認知水平。

仍以“3的倍數的特征”的教學為例。在學生獲得工具性理解的基礎上，教師創設一個“矛盾情境”：以111為例，學生根據1+1+1=3，判斷其是3的倍數；教師提醒學生注意111中三個“1”的實際數值，分別是1個百、1個十、1個一，此時教師停止講課，期待學生能發現其中的問題。果然，學生意識到：3個“1”的計數單位不同，為什么能相加呢？這個問題的發現和提出，給學生的認知和心理都形成強烈的沖突。當然，問題的解決需要教師提供“支架”、給予引導。比如，給學生如下方塊圖（如圖2），讓學生“圈圈畫畫，表示出1+1+1的意思，說明1+1+1是合理的”。學生經過研究，發現“1個百，圈掉33個3，也就是99，留下1；1個十，圈掉3個3，也就是9，留下1；還有個位的1（如圖3）。所以1+1+1，是3個1相加，不是1個百、1個十、1個一相加”。在此基礎上，教師再提供幾個數和方塊圖，如12、223等，讓學生圈、畫，加深理解。在之后的練習課上，教師再次提供這樣的素材：2的倍數，個位上是2、4、6、8或0；5的倍數，個位上是5或0；3的倍數，各數位上的數之和是3的倍數。啟發學生思考：能想到什么問題？學生提出：“為什么2和5的倍數特征看個位，而3的倍數的特征要看各數位上數的和？”學生通過對這個問題的深入探究及獲得的認知，實現對2、5、3的倍數的特征更高水平上（聯系和結構的水平）的關系性理解。這種理解，可以引導學生探究（比如推理）25、4、125、8、9的倍數的特征。

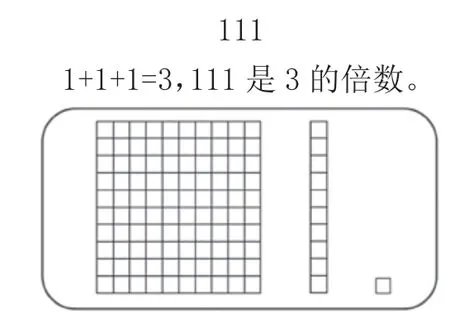
圖2

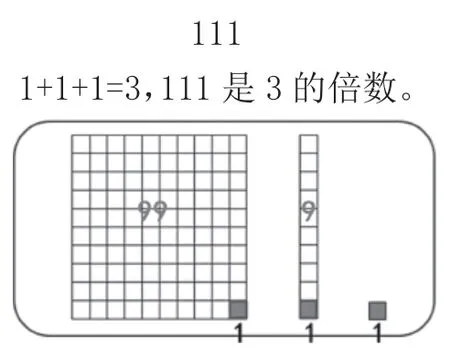
圖3

三、圍繞能力提升促進學生提出問題

這里所說的能力，是指學生數學問題提出的能力。正如“在游泳中學會游泳”，學生的數學問題提出能力也是在提出問題的學習、實踐與反思中提升的，反過來，能力的提升使學生在學習中更為主動地提出有效的數學問題。

（一）激發內在動機，促進主動提問

雖然培養學生“四能”（發現和解決問題的能力、分析和解決問題的能力）的課程目標已提出十多年，但是在數學教學中，“重解題輕問題”的思想意識在教師和學生中仍普遍存在。培養學生的問題提出能力，首要任務是培養學生在面對具體情境時，能主動提出問題來表達自己對這個情境的理解。一種可行的教學策略，是通過教師的引導，學生能提出問題并從提問的過程中清晰地感受自己在數學學習上的不斷進步，以此激發成就感，形成數學問題提出的內在動機。

比如，一年級學生對于問題“樹上有10只鳥，先飛走2只，再飛走5只。一共飛走了幾只鳥”常因思維定式做出錯誤的回答。教師改變教學策略，只提供情境“樹上有10只鳥，先飛走2只，再飛走5只”讓學生提出問題，學生提出“第一次飛走后樹上還剩幾只鳥”“一共飛走幾只鳥”“（兩次后）還剩幾只鳥”等問題。幾次的提問練習，使學生消除思維定式，能正確解題，初步感受發散、靈活思維的作用，對提問的興趣大大增強。

再如，教學“倍的認識”時，課始學生面對“藍花有2朵，黃花有6朵，紅花有8朵”的情境，能提出“藍花比黃花少幾朵”“黃花和紅花一共有幾朵”“三種花一共有幾朵”等問題；到課結束時，學生再次面對這一情境，發現自己還能提出“紅花朵數是藍花的幾倍”“黃花朵數是藍花的幾倍”這樣的問題，切實感受到自己數學知識的不斷豐富、本領的不斷增強，提問也就更加積極了。

又如，教學“簡易方程”，在鞏固練習環節，教師出示“鋼琴的黑鍵有36個，比白鍵少16個。白鍵有多少個？”“學校食堂原來有一些大米，吃掉16袋后，還剩36袋大米。食堂原來一共有多少袋大米？”學生列出方程，發現所列方程都是“x-16=36”。教師要求“再提出一些用x-16=36解決的問題”（讓學生根據算式或方程提出問題，是有意識的問題提出活動）。在提問中，學生加深了對方程意義的理解；全班交流后，看到那么多不同的問題能用同一個方程來表達等量關系，學生更深刻地體會到方程以及問題提出的價值。

（二）實現水平進階，促進有效提問

對于數學問題提出能力的水平劃分，學界有多種論述，其中張丹老師和吳正憲老師的觀點（如下表）易于一線教師在教學實踐中理解和把握。

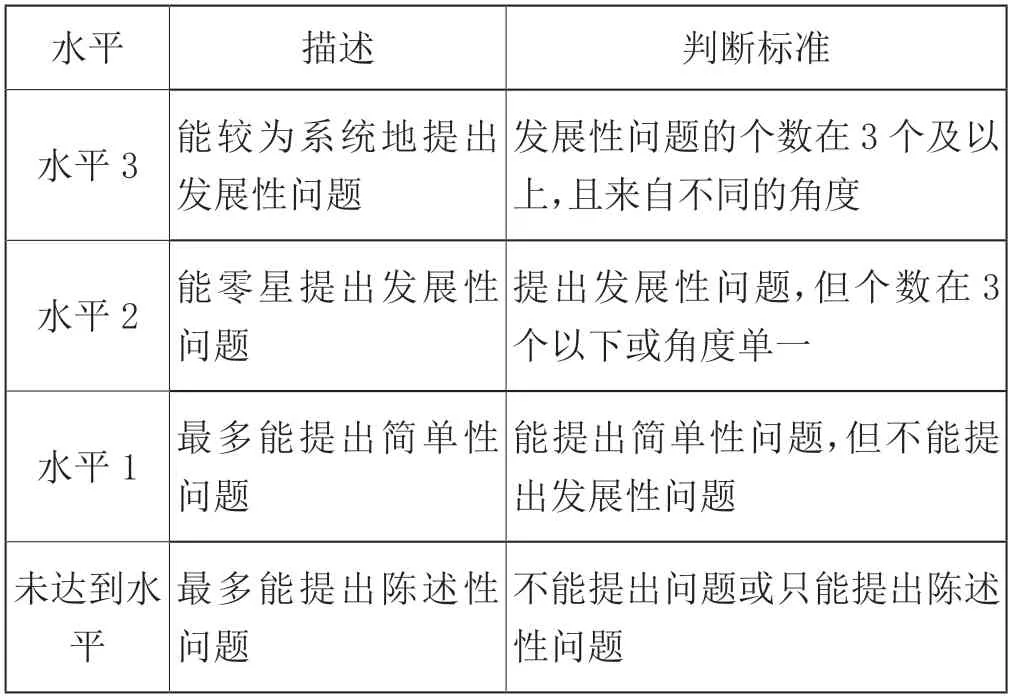
二至六年級學生問題提出的水平描述和劃分標準

實現學生提問水平進階的一種可行的教學策略，是教師創設開放的情境，既能讓不同水平層次的學生都能提出相應的問題，也能讓學生在提問后的師生交流活動中感悟不同問題之間的聯系和區別，產生提出高水平問題的愿望，并為之努力。

比如，用同樣的小正方形按一定的規律拼出下面四個圖形（如圖4）。已知每個小正方形的邊長是1厘米，請提出問題。

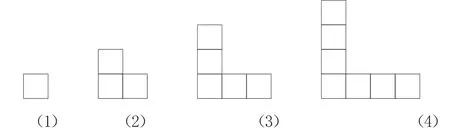
圖4

學生可以從圖形所用小正方形的個數、圖形的周長、面積等角度提問。下面，我們從圖形所用小正方形的個數角度，分析學生的提問水平：

未達到水平：第（4）個圖形有多少個小正方形？

水平1：第（5）個圖形有多少個小正方形？第（5）、第（6）、第（7）個圖形各有多少個小正方形？（所提問題，涉及的圖形和已畫出圖形是依次相鄰的）

水平2：第（10）個圖形有多少個小正方形？第（100）個呢？（所提問題，涉及的圖形不是相鄰的，已經初步具有規律意識，并試圖加以適當表征）

水平3：第n個圖形有多少個小正方形？（試圖將規律一般化，并用符號表征）如果有21個小正方形，拼成的是第幾個圖形？（具有逆向思考問題的意識，且能觀照每個圖形用到的小正方形是奇數個，思維具有一定的深刻性）

總之，支持學生數學問題提出，需要教師持續更新觀念，給問題提出以足夠的重視，加強理論學習，在教學實踐中積極探索，形成有效的、可供借鑒的教學策略，使問題提出成為數學教學活動的常態，從而對學生數學學習產生積極影響，學生能將問題提出作為數學學習不可分割的一個環節，主動提問、善于提問，促進數學學習質量不斷提升。