新型互補序列設計及其在OFDM系統(tǒng)改進同步算法中的應用

張爍瑜，高軍萍，李 琦，王 丹

（河北工業(yè)大學 電子信息工程學院，天津 300401）

0 引言

正交頻分復用（Orthogonal Frequency Division Multiplexing，OFDM）系統(tǒng)雖具有抗干擾能力強、頻譜利用率高的特點[1-4]，但其對時間和頻率偏移十分敏感[5-7]。在基于訓練序列的同步算法中，最為經(jīng)典的Schmidl 算法[8]由2 組相同序列構(gòu)成，但該算法因循環(huán)前綴（Cyclic Prefix，CP）的影響而存在一段“平坦區(qū)”。Minn算法[9]將訓練序列分為4部分，盡管該算法解決了“平坦區(qū)”的問題，但在定時估計曲線中存在一系列副峰，這會影響OFDM 系統(tǒng)的精確同步。Park[10]利用共軛對稱結(jié)構(gòu)提出一種新的算法，該算法的定時估計曲線在正確同步點有一個尖銳的峰值，同步較為準確，但副峰的存在仍可能會影響系統(tǒng)的正確同步。Schmidl、Minn和Park算法的訓練序列均采用相關性較差的PN序列，而互補序列因具有良好的相關特性引起學者們的關注[11]。相比較于MPSK Golay 互補序列而言，MQAM 序列因其優(yōu)良特性被更廣泛應用于OFDM 系統(tǒng)中。Chong 和Tarokh[12]基于4QAM 序列，提出2 種16QAM Golay 互補序列的構(gòu)造方法。2015 年，Zeng等[13]提出一種可將二元Golay互補序列直接生成16QAM Golay互補序列的設計方法。然而，目前互補序列的設計仍存在方法較少，長度受限的問題。

為提高OFDM系統(tǒng)的定時精度，本文利用相關性良好的新型互補序列對同步算法進行改進。首先，設計出一種新型16QAM Golay互補序列，該序列因具有良好的相關特性可以有效地應用于OFDM系統(tǒng)中；然后，利用新型互補序列和恒包絡零自相關（Constant Amplitude Zero Auto Correlation，CAZAC）序列提出一種同步改進算法，該算法利用共軛對稱結(jié)構(gòu)，采用2組序列對原有的滑動窗口進行改進，通過對設計的2組窗口同時進行相關運算，可很好的解決系統(tǒng)在低信噪比下對定時偏移尤為敏感的問題。仿真結(jié)果表明，改進算法在低信噪比下仍可實現(xiàn)精準同步，并且副峰對主峰的影響較小，能夠提高系統(tǒng)的定時精度。

1 新型Golay 互補序列的設計

由于OFDM 系統(tǒng)對定時偏移較為敏感，應用相關性良好的互補序列可以提高系統(tǒng)的定時精度。因此，本節(jié)提出一種新型16QAM Golay互補序列的設計方法，為互補序列在同步中的應用提供了更多的可選序列。

1.1 Golay 互補序列的定義

Golay[14]在1961年首次定義了Golay互補序列，通常采用自相關函數(shù)對其進行表征，定義如下：

定義1設序列u=(u0,u1,…,un-1)，其非周期自相關函數(shù)為

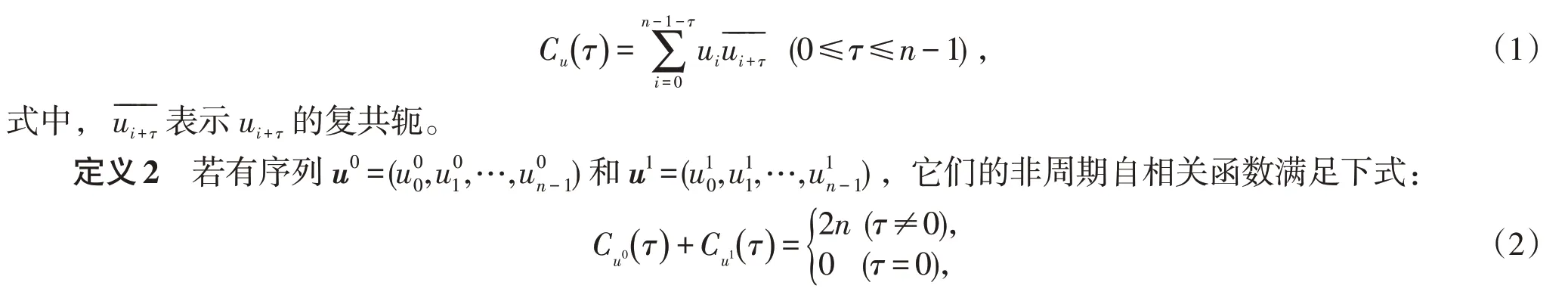
則稱(u0,u1)為Golay互補序列對。

基于上述Golay互補序列對的思想，Tseng[15]提出Golay互補序列集，定義如下。

定義3若有m個長為n的序列(u0,u1,…,um-1)滿足：

則稱(u0,u1,…,um-1)構(gòu)成一組Golay互補序列集。

1.2 新型16QAM Golay 互補序列的構(gòu)造方法

首先，定義一組通過二元序列u0,u1得到十六元序列v0,v1,v2,v3的新型映射方法，如下：

新型16QAM Golay互補序列構(gòu)造步驟如下：

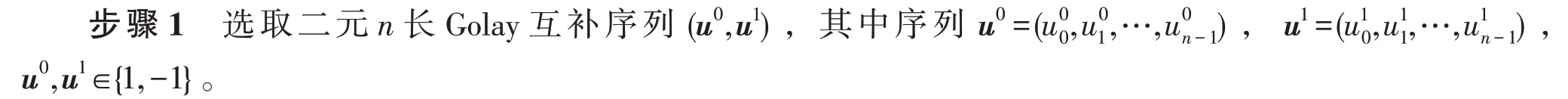
步驟2利用式（4）所定義的新型映射關系，將序列(u0,u1)進行變換，可得到一組n長16QAM序列集(v0,v1,v2,v3)。

步驟3通過級聯(lián)將(v0,v1,v2,v3)擴展成長度為2n的序列集(w0,w1,w2,w3)，如下：

定理1如果存在一組n長二元Golay互補序列(u0,u1)，通過式（4）變換得到序列(v0,v1,v2,v3)，則該組序列(v0,v1,v2,v3)為Golay互補序列。

證明：根據(jù)自相關函數(shù)定義，

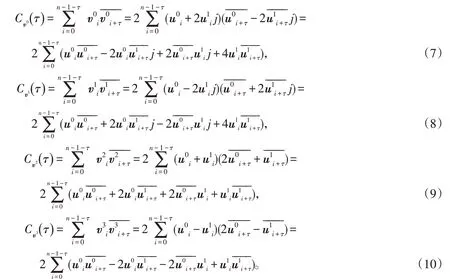
因此，

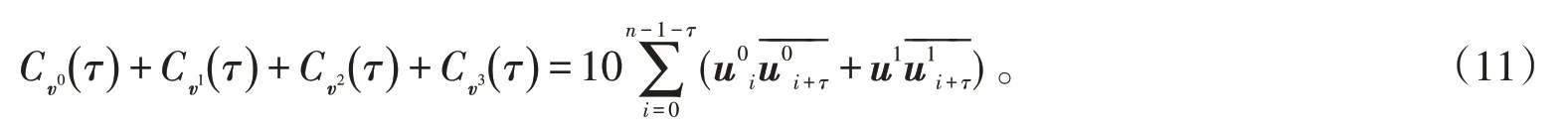
已知(u0,u1)為一組Golay互補序列，根據(jù)該序列自相關性質(zhì)，可得

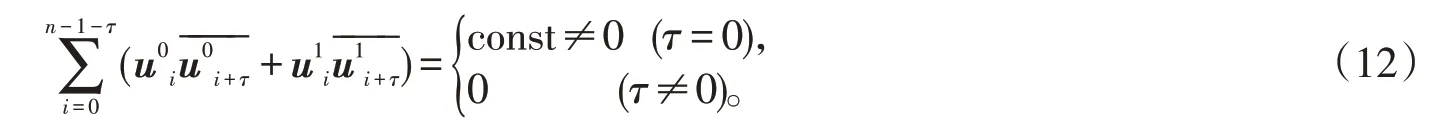
所以，

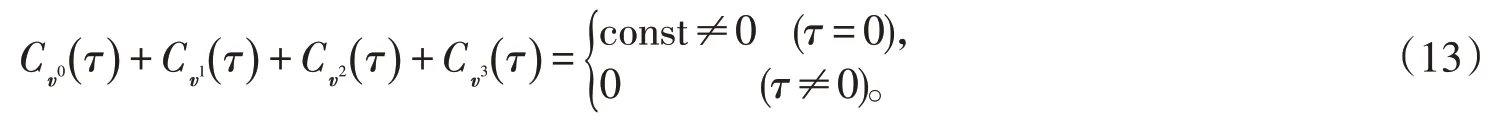
綜上，(v0,v1,v2,v3)為Golay互補序列。

定理2若有一組n長Golay 互補序列(v0,v1,v2,v3)，則其通過式（6）的級聯(lián)方法所得到的序列(w0,w1,w2,w3)也為Golay互補序列。

證明：根據(jù)自相關函數(shù)定義，

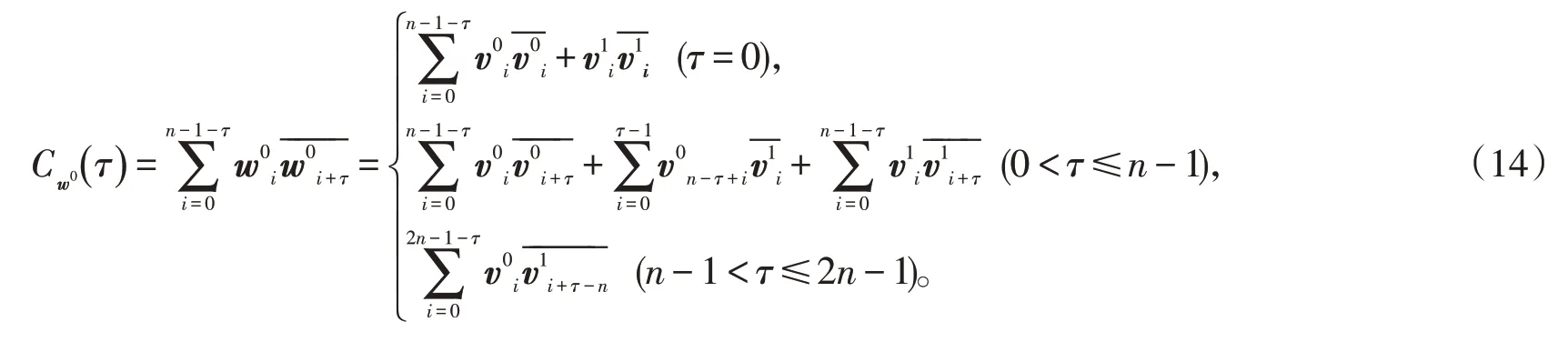
同理可得，

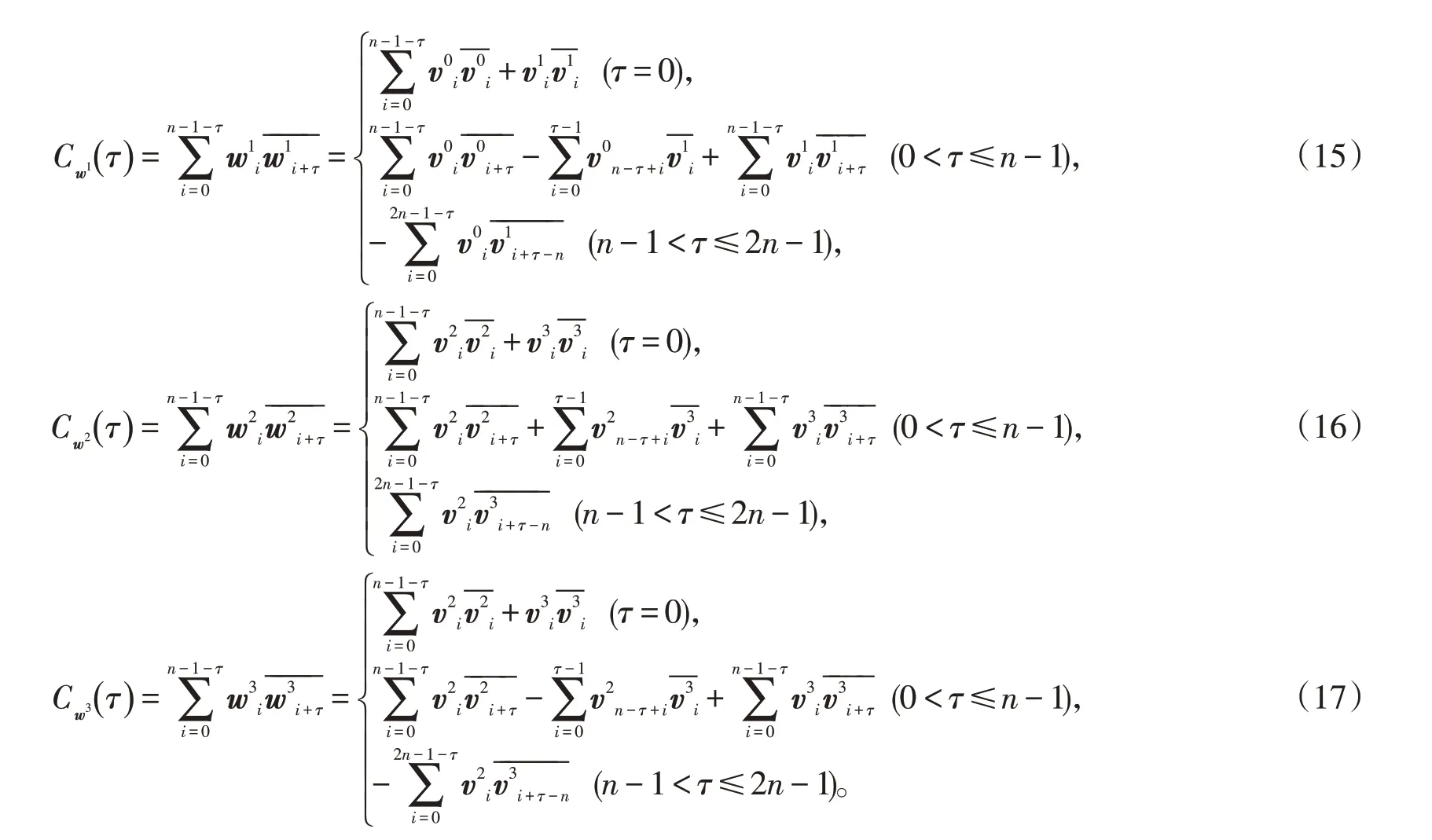
因此，

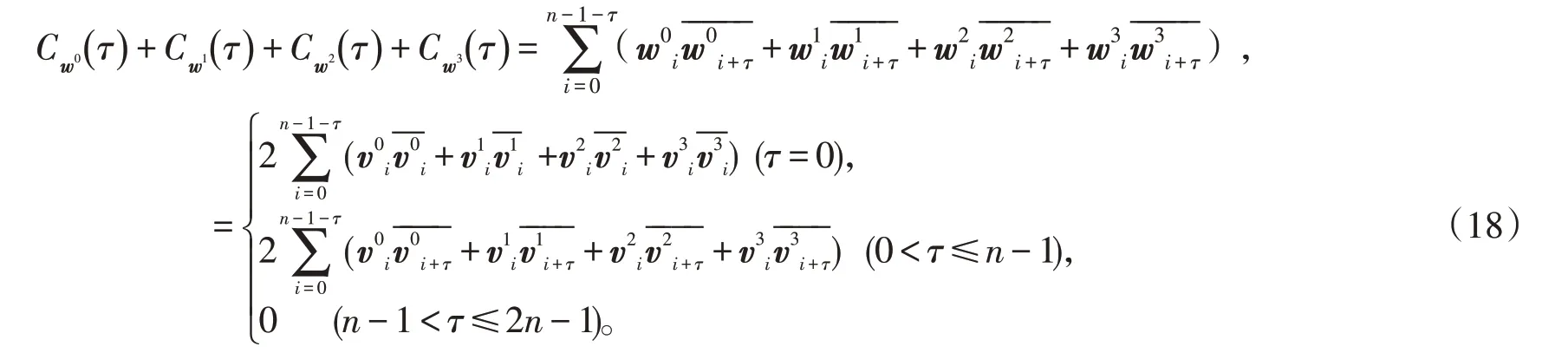
已證(v0,v1,v2,v3)為Golay互補序列，根據(jù)定義3可知：

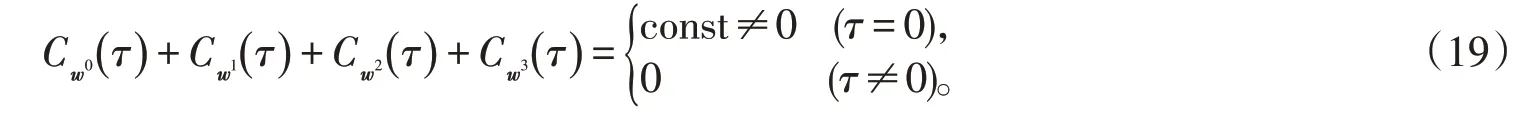
因此，序列(w0,w1,w2,w3)為一組Golay互補序列。

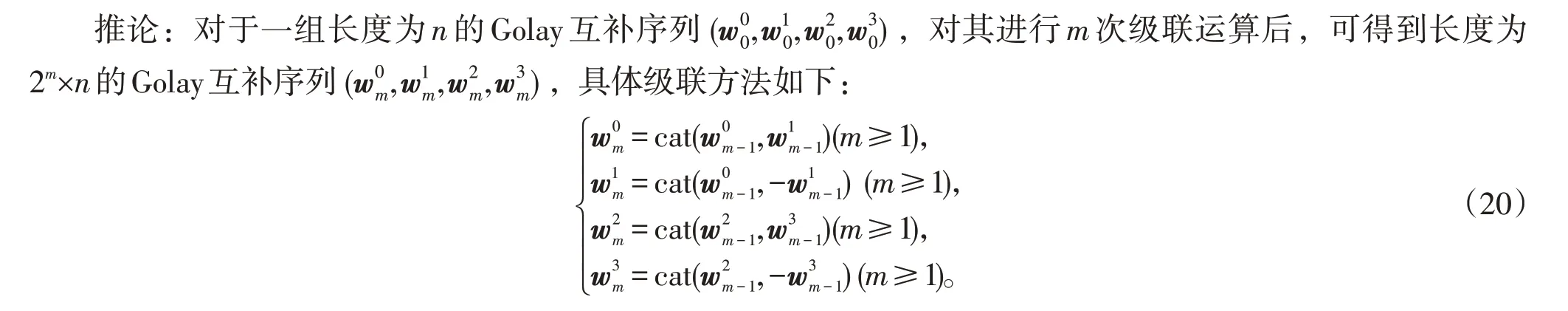
證明：根據(jù)序列的自相關特性，

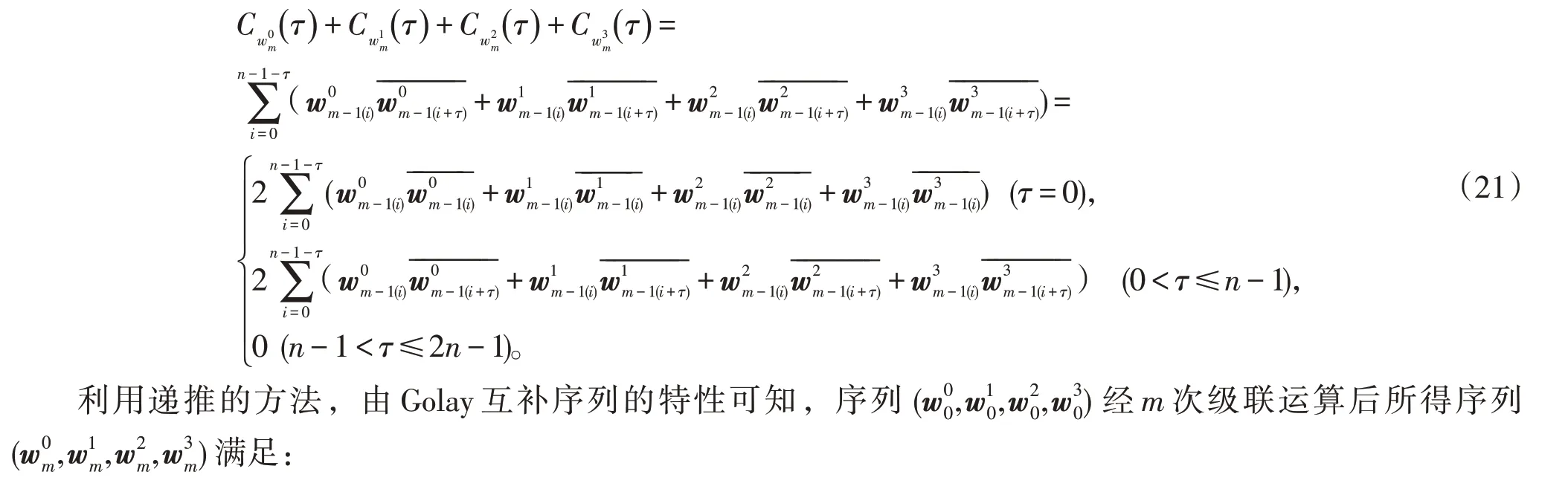
因此，推論成立。

表1對比了部分Golay互補序列的構(gòu)造方法。現(xiàn)有的一些構(gòu)造方法所設計的序列長度受限，僅能得到單一長度的序列，而本節(jié)提出的Golay 互補序列長度可根據(jù)初始序列長度和級聯(lián)次數(shù)的不同，靈活得到多種可選序列。例如：若想得到長為16 的Golay 互補序列，利用本節(jié)提出的設計方法，可通過選取初始序列長度分別為2、4、8 的序列，并對應級聯(lián)3、2、1 次的3種方法生成。另外，若想得到非2次冪長度的Golay互補序列，只需選取長度為非2次冪的初始序列并結(jié)合級聯(lián)就可生成。

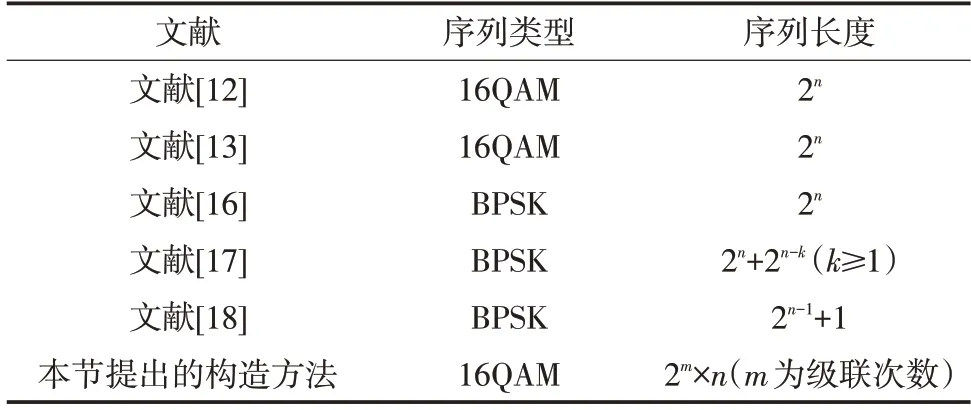
表1 Golay 互補序列構(gòu)造方法對比Tab.1 Comparison of construction methods of Golay complementary sequences

1.3 構(gòu)造實例

選取長度為4 的二元Golay 互補序列對(u0,u1)，如下：

由式（4），可構(gòu)造長為4的16QAM Golay互補序列(v0,v1,v2,v3)：

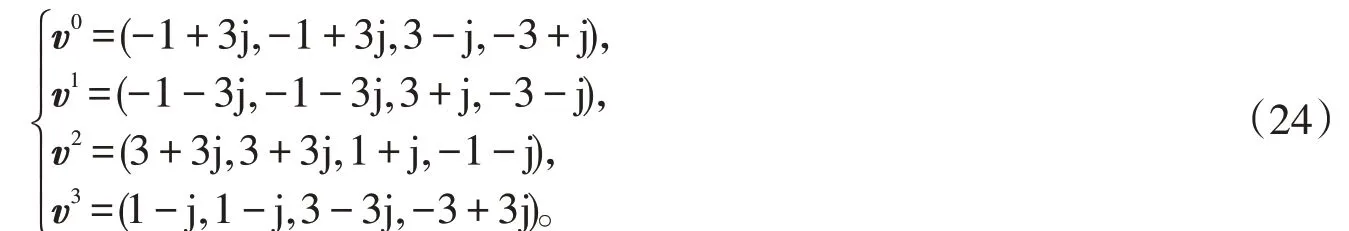
利用推論中的方法，將(v0,v1,v2,v3)級聯(lián)2次后，可得到長為16的16QAM Golay互補序列

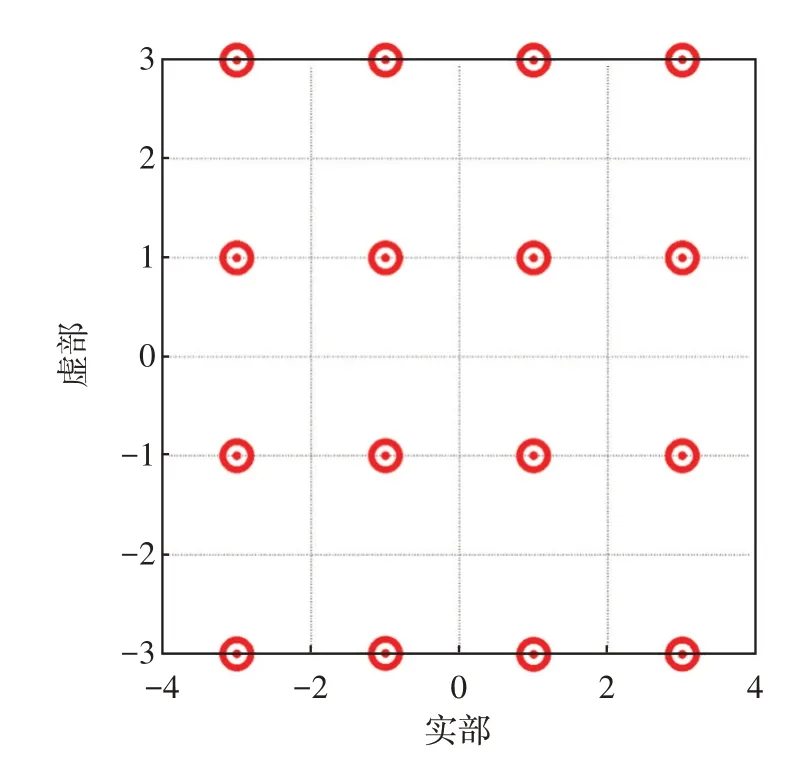
圖1 星座圖Fig.1 Constellation of sequence

2 新型互補序列在同步技術(shù)中的應用

由于OFDM 系統(tǒng)在低信噪比下對定時偏移更為敏感，本節(jié)通過對訓練序列結(jié)構(gòu)重新進行設計，利用新型16QAM Golay互補序列和CAZAC序列對滑動窗口進行改進，提出一種改進同步算法。

2.1 OFDM 系統(tǒng)同步原理

在含有N個子載波OFDM 系統(tǒng)中，信號采樣值為[19]

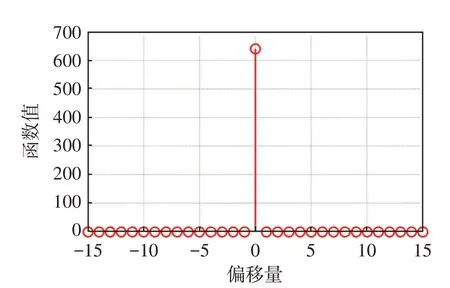
圖2 序列自相關特性Fig.2 Subsequence Autocorrelation Properties

式中：xn表示在第n個子載波上的傳輸信號；k為采樣點。

若信號在接收端完成精準采樣，則接收端的第k個采樣值為

式中：θ為符號定時偏移；Δfc為歸一化后的頻率偏移值；n(k)為第k個采樣值的加性高斯白噪聲（Additive White Gaussian Noise，AWGN）；接收信號y(k)由式（28）表示：

式中：L表示信道容量；h(l)為第l個信道的脈沖響應。

基于訓練序列的同步算法的定時度量函數(shù)M(d)可由式（29）表示：

式中：P(d)表示滑動窗口的相關函數(shù)；R(d)表示接收機在滑動窗口d采樣點時的能量。

2.2 基于新型互補序列和CAZAC 序列的改進同步算法

本節(jié)提出一種基于新型互補序列和CAZAC 序列的改進算法，該算法采用共軛對稱結(jié)構(gòu)，將訓練序列分，4個部分：[A B*C D*]。其中，A是長度為N/4的互補序列，序列B為A的對稱序列，C是長度為N/4的CAZAC序列，序列D為C的對稱序列，符號“*”表示共軛運算，CP表示循環(huán)前綴，具體結(jié)構(gòu)可表示為：

基于2 組不同的序列，改進算法分別利用2 個不同的滑動窗口進行相關運算。滑動窗口1 設置為互補序列，窗口2 為CAZAC 序列，且兩窗口相距N/2。在該算法的窗口滑動過程中，只有當2個窗口同步點的相關值均為最大值時，所對應的才為正確同步點。為方便分析，將序列A，B*，C，D*分別表示為[a b]，[b*a*]，[c d]，[d*c*]，改進算法的滑動相關運算如圖4所示：

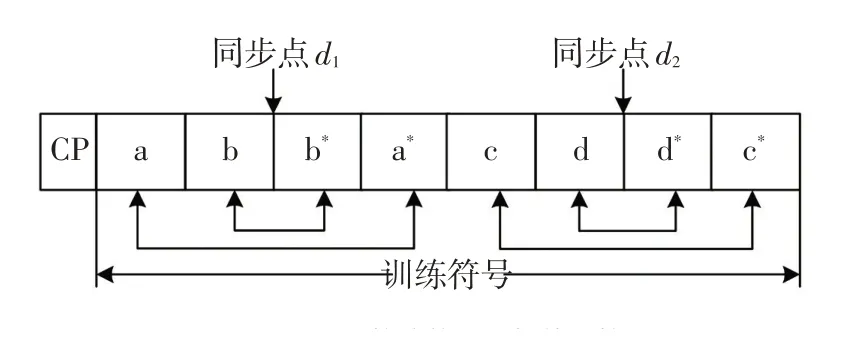
圖4 改進算法的滑動相關運算Fig.4 Sliding correlation operation of proposed algorithm

由于改進算法利用2 個窗口進行滑動相關，根據(jù)訓練序列的結(jié)構(gòu)特點，該算法將2 個滑動窗口的Pi(d)和Ri(d)分別表示為

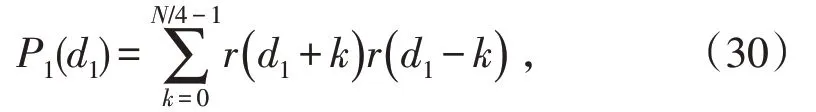
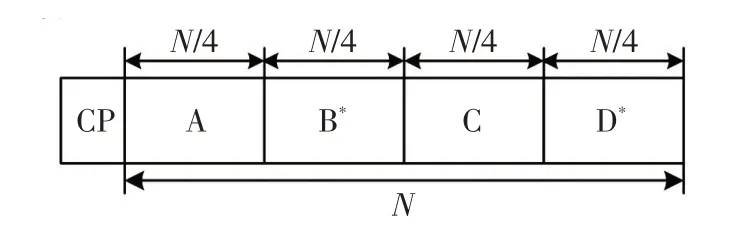
圖3 改進算法的訓練序列結(jié)構(gòu)Fig.3 Training sequence structure of proposed algorithm

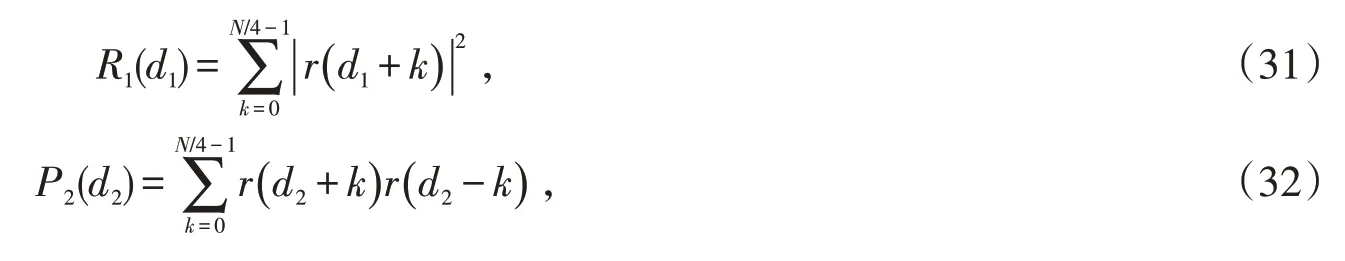
改進算法的定時度量函數(shù)表示為

式中：Pi(d)表示第i個滑動窗口的相關函數(shù)；Ri(d)表示接收機在第i個滑動窗口d采樣點時的能量。

根據(jù)式（34）可知，當2 個窗口的定時度量函數(shù)為非峰值（即Mi（d）≠1）時，根據(jù)乘法運算的性質(zhì)，改進算法的定時度量值接近于0，只有當2個滑動窗口的定時度量函數(shù)同時達到最大值時，此時才得到該算法定時度量函數(shù)的峰值。

改進算法的同步點置于訓練符號起始位置N/4處，故定時同步點的估計值為

3 仿真結(jié)果分析

利用MATLAB 對OFDM 系統(tǒng)的幾種不同算法：Schmidl 算法、Minn 算法、Park 算法以及改進同步算法，在低信噪比（Signal to Noise Ratio，SNR）下的定時估計曲線和峰值比進行仿真分析。

3.1 低信噪比下的定時估計曲線分析

圖5 表示在CP=N/4，SNR=5 dB 條件下，4 種同步算法的定時估計曲線。圖5（a）中，Schmidl 算法由循環(huán)前綴引起的“平坦區(qū)”會導致該算法無法進行準確同步；Minn算法在正確同步點位置附近存在著幾乎與主峰等高的副峰，嚴重時，副峰值可能會超過在正確同步點處的主峰值，無法進行精準同步；在Park算法的定時估計曲線圖中，雖然主峰尖銳，但由于循環(huán)前綴的存在，該算法的定時估計曲線在正確同步點附近仍會存在多個副峰；而在圖5（b）改進算法的定時估計曲線中，幾乎無副峰，僅在正確同步點處存在一個十分尖銳的峰值。仿真結(jié)果表明，改進算法在低SNR的情況下，主峰完全不會受到副峰的干擾，能夠?qū)崿F(xiàn)精確同步。

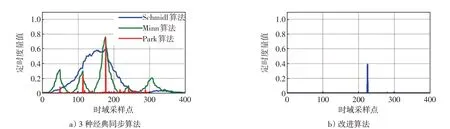
圖5 4 種同步算法定時估計曲線Fig.5 The Timing Estimation Curves of Four Synchronization Algorithms

3.2 峰值比分析

副峰對主峰的干擾通常是影響OFDM系統(tǒng)正確同步的最主要原因，為直觀描述這一特性，現(xiàn)將峰值比定義如下。

定義4將最高副峰幅值與主峰幅值之間的比值定義為峰值比，具體可用式（37）表示：

式中：P1表示最高副峰的幅值；Pm表示主峰的幅值。

圖6所示為4種不同的同步算法在AWGN信道，CP=N/8，不同SNR條件下仿真500次時的Pr。從圖中可發(fā)現(xiàn)，Schmidl算法、Minn算法受訓練序列中的重復結(jié)構(gòu)以及循環(huán)前綴的影響，其Pr較高；而Park算法雖較前2種算法而言Pr有所降低，但仍明顯高于改進算法的Pr。根據(jù)式（37）可知，Pr越高，則說明最高副峰的幅值與主峰幅值之間差距越小，反之Pr越低，則說明最高副峰的幅值與主峰幅值相差越大。由此可見，改進算法的副峰對主峰的影響較小，有利于在OFDM系統(tǒng)中完成精準同步。

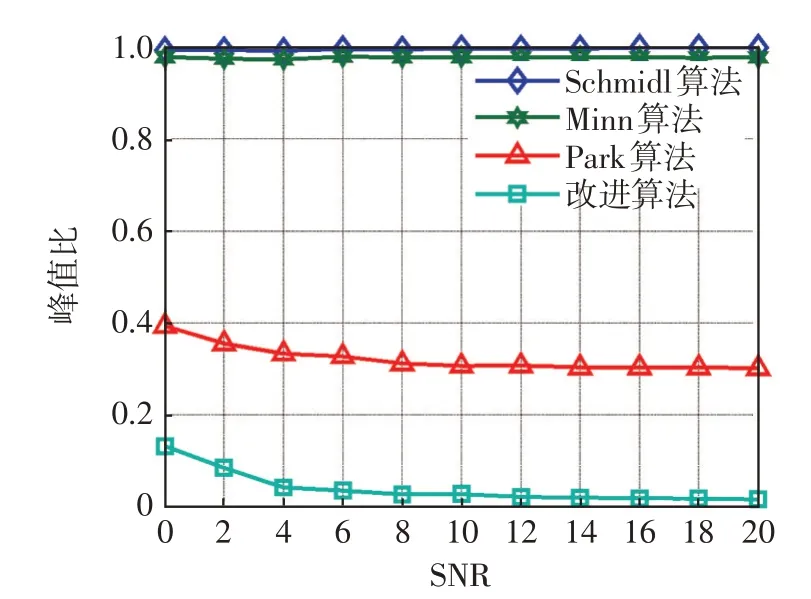
圖6 4 種同步算法的峰值比Fig.6 Peak ratio of four synchronization algorithms

4 結(jié)語

由于OFDM系統(tǒng)對定時偏移較為敏感，互補序列因具有良好的相關特性可應用于該系統(tǒng)中。同時，為解決系統(tǒng)在低信噪比下仍存在定時精度差的問題，還需對系統(tǒng)中的同步算法進行改進。為此，本文首先提出一種新型16QAM Golay互補序列的設計方法，然后利用新型互補序列和CAZAC序列提出一種改進同步算法。該算法通過對原有的滑動窗口進行改進，采用2組滑動窗口同時對2組不同的序列進行同步，以此解決系統(tǒng)在低信噪比下對定時偏移更為敏感的問題。仿真結(jié)果表明，改進算法較經(jīng)典同步算法而言，副峰對主峰的干擾較小，能夠提高系統(tǒng)的定時精度。