一種分析膜面在積水荷載作用下響應的數值模型

膜結構由于具有輕質、高強、美觀等優點而廣泛應用于體育館、游泳館等建筑.膜結構為柔性結構，在平面外荷載作用下，容易產生較大變形，比一般建筑結構更容易積水，進而產生袋狀效應，引起膜面破壞或結構坍塌，因此膜結構找形設計時應考慮足夠的排水坡度.但對于大跨充氣膜結構等，其頂部不可避免地會存在較大平緩段，存在積水安全隱患.所以研究膜面在積水作用下的響應(如變形和應力)對實際工程具有十分重要的意義.

該廠通過本次查找泄漏并對漏點處理后，在隨后進行的真空嚴密性試驗中，低壓側凝汽器真空泄漏速度為90Pa/min、高壓側為60Pa/min，相比處理前的真空嚴密性試驗數據（低壓側350Pa/min、高壓側260Pa/min）有了明顯的改善。

膜材作為一種復合材料，合適的本構模型能有效地反映膜材的力學性能，是膜結構受力分析的關鍵.目前，主要通過單軸拉伸試驗和雙軸拉伸試驗測量膜材的力學性能.大多數設計指南和規范推薦使用基于平面應力正交各向異性的假設，采用最小二乘法計算彈性參數.但隨著人們對分析結果要求的提高，單一不變的彈性參數已不能滿足使用需求.Gao等通過不同經緯向應力比的雙軸拉伸試驗數據得到經緯向應力-應變響應面和彈性參數響應面，并通過Abaqus的UMAT子程序實現非線性本構，理論分析模型與實驗數據的吻合體現出該方法的優越性.

膜面的積水過程涉及膜面大變形、水和膜面的耦合作用.一些學者采用理論分析和試驗研究了積水作用下的膜面響應，吳明兒等使用ANSYS軟件分析了正方形平面膜和氣枕膜的積水承載能力以及不同跨度和矢跨比對積水過程的影響.張影等基于向量式有限元提出了膜結構的破壞準則，分析了強降雨作用下充氣膜結構積水過程的發展和破壞模式.文獻[12]將膜結構求解器和體積守恒求解器耦合，給出了整體和分區方法計算給定積水體積下膜結構的靜態變形.以上分析均是基于變形和荷載相互影響的迭代算法模擬積水過程，但模擬過程比較復雜.目前Abaqus等商業軟件可以同時處理非線性大變形和流固耦合的問題，如顯式動力學模塊中光滑粒子流體動力學(SPH)方法.

G是當前像素值，W和H分別是圖像的寬和高，由于圖像經過了二值化，故圖像中只存在0或者255兩個值，利用其作為標志，當合并符合約束條件的種子后，將其像素設置為0.最后，當圖像中僅存在全為0的像素時，算法終止.以圖5為例，其分割后效果如圖6所示.

為了能夠得到膜面在積水荷載作用下更為精確的響應分析結果，本文將SPH方法和膜材非線性本構模型相結合，用光滑粒子模擬水，使用平滑分析步，從而得到一種分析積水荷載作用下膜面響應的數值模型，并將數值分析的最大變形與試驗結果進行了對比分析，驗證了本文提出的數值模型的適用性和可靠性.

1 非線性本構模型

1.1 雙軸拉伸試驗

雙軸拉伸試驗使用Ferrari 1202 S2膜材，試件為十字形，在上海交通大學研制的雙軸拉伸試驗機上進行.考慮不同應力比的影響，試驗選取了9組應力比(1∶1、1∶2、2∶1、1∶3、3∶1、1∶5、5∶1、1∶0、0∶1)，每組應力比采用一個全新試件進行單次拉伸直至破壞，加載前設置1.25 kN/m的預應力，保證試件不會松弛.

1.2 應力-應變響應面

使用常用的二元二次多項式對試驗數據進行擬合：

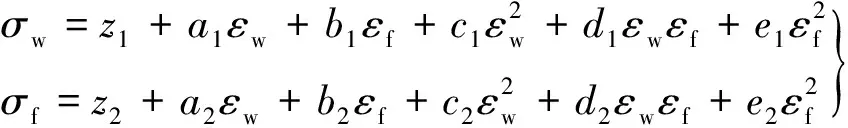
(1)

式中：、分別為膜面經向及緯向應力；、、、、、為膜面經向多項式系數；、、、、、為膜面緯向多項式系數；、分別為膜面經向及緯向應變.各系數取值如表1所示.經向應力-應變響應面和緯向應力-應變響應面擬合均方差分別為0.987和0.986，擬合結果如圖1所示.

1.3 本構模型

在Abaqus軟件中，可使用Abaqus/Standard和Abaqus/Explicit分析模塊對膜結構分別進行靜力通用分析和動力顯式分析.同時Abaqus通過FORTRAN程序接口提供許多用戶子程序，其中UMAT和VUMAT是提供給用戶自定義材料屬性的接口(分別對應Standard和Explicit).根據Newton迭代法的計算原理，UMAT和VUMAT子程序的主要任務是根據Abaqus主程序傳入的應變增量更新應力增量，即根據已知時刻的應力、應變等狀態變量得到+Δ時的應力：

+Δ=+d=+d

(2)

式中：+Δ為+時膜面應力；為時膜面應力；d、d分別為Δ時間內膜面的應力增量、應變增量；=?Δ/?Δ為Jacobian矩陣.膜面采用膜單元時，僅考慮=[]，=[]，、分別為膜面的切應力、切應變.

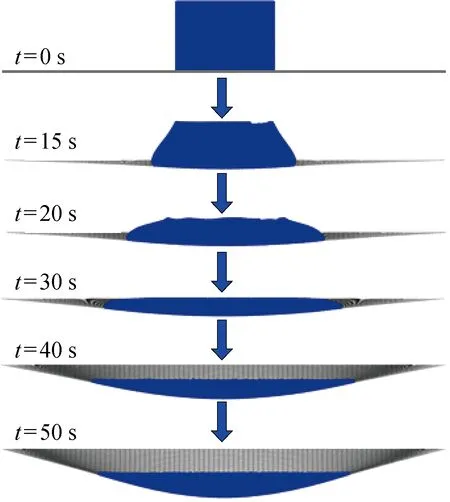
..加載過程 采用平滑分析步的方式將重力從0緩慢增加到設定值，使水荷載的加載變得平緩，水粒子之間的約束使水柱在加載過程中始終為一個整體.當加載時長為100 s，隨著重力的增加，水往下運動，膜面緩慢變形.同時水柱下表面與膜面形狀始終保持一致，上部的水粒子不斷向下、向周圍擴散，約40 s時水柱的上表面邊緣與膜面接觸，而后重力繼續增加，膜面的變形也不斷增加，100 s時重力加載完畢，膜面和水荷載達到靜態平衡，如圖5所示.

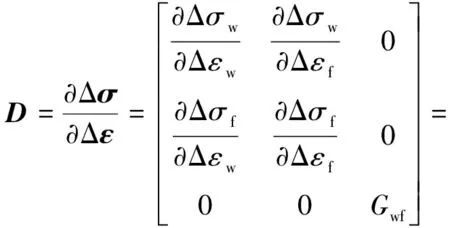
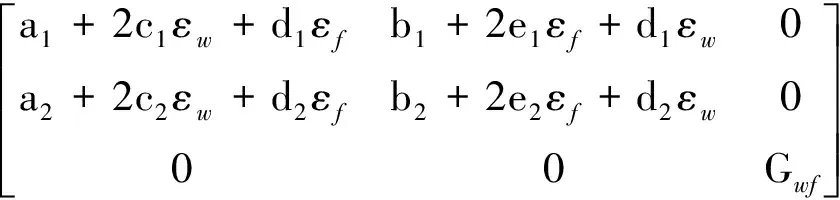
(3)

式中：為切變模量，取工程經驗值200 kN/m.在VUMAT子程序中獲取時刻的應變計算Jacobian矩陣，然后根據式(2)，實現應力的更新.

2 膜面積水數值模擬

2.1 SPH方法原理

SPH方法是一種無網格、拉格朗日性質的質點方法，在有限元分析中不需要定義節點和元素，只需要一個點集合表示給定的主體.它本質上與有限元方法相似，是求解偏微分方程組的離散化方法，使用插值方法近似域內任意一點的常變量，一個質點上的值可以用一組臨近粒子的貢獻的累加來近似.SPH方法僅可在Abaqus的顯式動力學分析中實現.

2.2 有限元模型

圖9、10分別為各級荷載作用下膜面的最大應力和最大應變與積水荷載的關系曲線，圖中為主應變.從圖9可以看出，隨著積水荷載增加，最大Mises應力及最大經緯向應力逐漸增大，且緯向應力始終大于經向應力，兩者差值由自重作用下的0.4 kN/m增加到3.2 t積水荷載作用下的0.9 kN/m，而后逐漸減小到了8.4 t積水荷載作用下的0.5 kN/m.Mises 應力數值介于經向應力和緯向應力之間，從 3.3 kN/m 增加到19.1 kN/m.將膜面的最大Mises應力與積水荷載的關系進行曲線擬合，可得

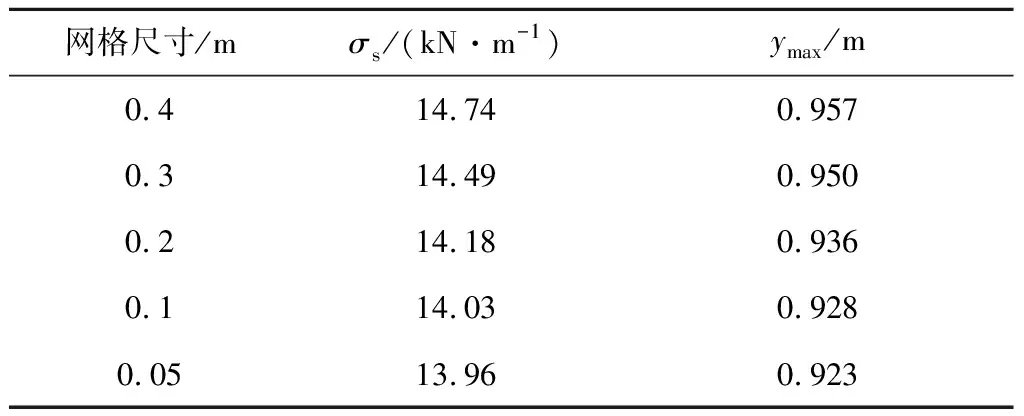
..網格尺寸 通過分析不同網格尺寸的有限元模型驗證收斂性.網格尺寸越小，計算結果越精確，但是計算時間成本將會增加.結果表明，計算結果與膜面網格與水柱網格尺寸的比例(下文簡稱為網格尺寸比例)及網格尺寸的大小有關.以4.5 t水荷載為例，分析不同網格尺寸比例和不同網格尺寸大小的有限元模型.

水荷載采用Abaqus動力顯式分析步中SPH方法模擬，具體方法為先用八結點線性六面體單元(C3D8R)對一定體積的水柱進行網格劃分，然后將每個單元轉化為一個粒子，用粒子模擬水荷載.在水的加載過程中，水的流動近似為不可壓縮和黏性層流的流動.采用線性Us-Up的Mie-Gruneisen狀態方程描述水的壓力：

由此，四則運算的計算方法有機地連結起來，從而構成了一個完整的知識結構．如此，可能會使教師對四則運算的計算原理（數學測量的可公度性原理）獲得深層次的理解，從而為有品質的數學課堂的改進和提升提供方向．

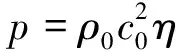
(4)

式中：=1 000 kg/m為擾動前水的密度；=1 500 m/s為沖擊波波速；=1-為名義體積壓縮應變，為擾動引起變化的流體密度.采用牛頓黏性剪切模型定義剪切響應：

=1078-5365e-167-9932e-742

(5)

對該懸掛系統,考慮滾輪處調心滾子軸承需維護更換,其中，y1=1.675 kg,x2=20,x3=13,y2=13,y3=13,代入式(2),得液壓式懸掛方案更換一個懸掛輪軸承的平均更換時間TB=258 min.

本文采用動力顯式分析，水的初始狀態為置于膜上表面的水柱(水柱半徑設置為1 m)，分析結果表明水在瞬時重力作用下加載于膜面時，膜面會發生上下往復運動，且很難穩定.這是因為膜的外力功(水柱的重力勢能)有一部分轉化為動能，而沒有全部轉化為內能.一般在動力分析中為了使位移荷載加載過程為準靜態，采用加載速度和加速度均光滑的平滑分析步施加位移荷載，如圖3所示.因此，為了避免重力荷載加載過程中產生過多動能，以平滑分析步的方式施加重力荷載，即荷載幅值在加載時間段[，+1]滿足：

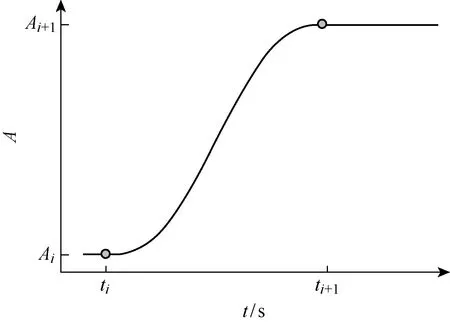
=+(+1-)(10-15+6)

(6)

式中：為時刻的荷載幅值；=(-)(+1-)為無量綱中間量.

2.3 準靜態加載過程分析

膜采用四結點四邊形膜單元(M3D4R)模擬.膜的材料屬性采用1.3節中的非線性本構模型，并通過VUMAT子程序進行定義，同時定義瑞麗阻尼減少膜面振動.

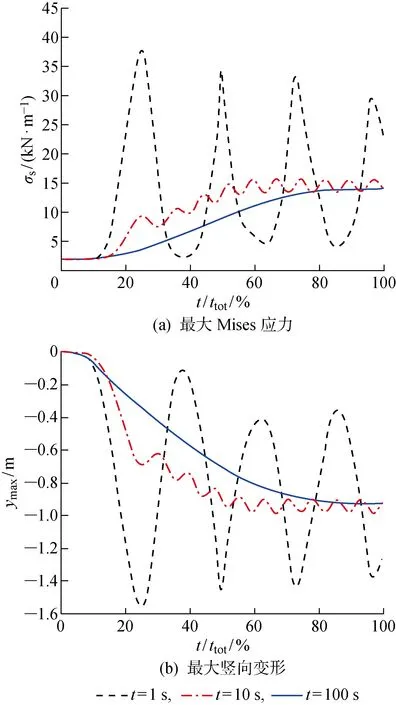
..加載時長 為了研究加載時長對分析結果的影響，以4.5 t積水荷載為例，建立3種不同加載時長(=1,10,100 s)的有限元模型，并在加載步后設置5 s的穩定階段，觀察膜面的響應.加載過程及穩定階段的、與分析進程(，為分析所用總時間)變化曲線如圖4所示.可以看出，當加載時長為1 s時，加載過程中膜面的最大Mises應力和最大豎向變形一直增大，但加載完畢后的5 s內，兩者發生上下往復的波動，最大Mises應力在 2.5～38 kN/m變化，最大豎向變形在-0.1～-1.6 m(負號表示變形方向向下)范圍變化.當加載時長為10 s時，整個過程中膜面的最大Mises應力和最大豎向變形總的趨勢是一直增大的，但在后半段加載過程及加載完畢后的5 s內，兩者會發生上下往復的波動，最終最大Mises應力的上下變化幅度穩定在5 kN/m左右，最大豎向變形的上下變化幅度穩定在0.1 m左右.當加載時長為100 s時，加載過程中膜面的最大Mises應力和最大豎向變形一直平滑增加，最終最大Mises應力穩定在 12.5 kN/m 左右，最大豎向變形穩定在0.9 m左右，且兩者的曲線形狀與平滑分析步的形狀相似.因此可以得出加載時間為100 s時，分析過程可視為靜態分析，滿足分析要求.

將膜面網格尺寸設置為0.1 m，分別研究 1∶2、1∶1、1.5∶1、2∶1、3∶1共5種不同網格尺寸比例對計算結果的影響.結果表明，當網格尺寸比例大于2∶1時，隨著網格尺寸比例的增加，應力和變形變化不明顯，如表2所示，表中為膜面最大 Mises 應力；為膜面最大豎向變形.保持網格比例為2∶1不變，研究5種網格尺寸(膜面網格尺寸分別為0.4、0.3、0.2、0.1、0.05 m)對計算結果的影響.結果表明，當膜面網格尺寸小于0.1 m時，隨著網格尺寸減小，應力和變形變化不明顯，如表3所示.因此本文后續的膜面積水有限元模型采用網格尺寸比例為2∶1，膜面網格尺寸為0.1 m，水柱網格尺寸為 0.05 m.整個膜面由 8 100 個大小相同的網格單元組成，每個膜單元的面積為0.01 m，水柱網格(SPH粒子)密度約為 9 603 個/m.

張麗清：華中師范大學C100計劃，主要是通過聯盟、合作、創新，依托大學教育的特色發展優勢，廣泛整合校內優質教育資源，推進合作區域內教育的高位均衡、多元發展。華中師范大學在合作辦學方面提出三個目標，一是在基礎教育方面開展綜合改革，二是建立基礎教育新的教育教學體系，三是以推進教育信息化來推動教育體制改革。在“互聯網+”時代，教學改革主要是通過華中師范大學和政府合作辦學，與地方政府、大集團合作，還有就是實現三方合作，政府、機構和大學一起成立學校董事會，培訓職業校長，同時管理合辦學校。

對于傳統線性材料模型，Jacobian矩陣均為確定的值，但膜材屬于非線性材料，Jacobian矩陣與此時的應力(應變)水平相關.以Ferrari 1202 S2膜材為例，根據1.2節中經緯向應力的表達式(1)可以得到Jacobian矩陣的表達式：

3 數值模擬結果分析

3.1 膜面變形

為了驗證采用SPH方法與膜材非線性本構結合進行數值分析的可靠性，將數值模擬得到的膜面變形與試驗測得的膜面變形進行比較.

高校聯盟是“在兩個或兩個以上的高校（或高校與其他特定組織、機構）之間，圍繞某一共同的戰略目標，通過協議或聯合組織等方式建立起來的互為補充、共擔風險、相互銜接的一種聯合體”[4]47-49。在科學的建設理念指導下，聯盟有條不紊地運行，健康發展，產生了“1+1＞2”的良好效應。

..平膜積水試驗模型 試驗模型為正方形Ferrari 1202 S2平膜，由6片單層Ferrari膜片焊接而成，通過鋁夾和螺栓固定于邊長為9 m的支撐結構上，如圖6所示，調整支撐結構使膜面保持水平.通過懸掛于膜面上方的水管施加水荷載，并使用帶有刻度的水桶控制加載.為研究膜面在積水荷載作用下的變形發展過程及應力變化，使用分級加載方式，將0～8.4 t水共分為11級.為了測量膜結構的幾何形狀，每次加載完后停留2 min，待膜面變形穩定后，將3D激光掃描儀固定于歸心盤后置于地面，進行掃描測量膜面形狀.激光掃描儀可以準確記錄膜面各點的三維坐標，以此獲得膜面形狀.

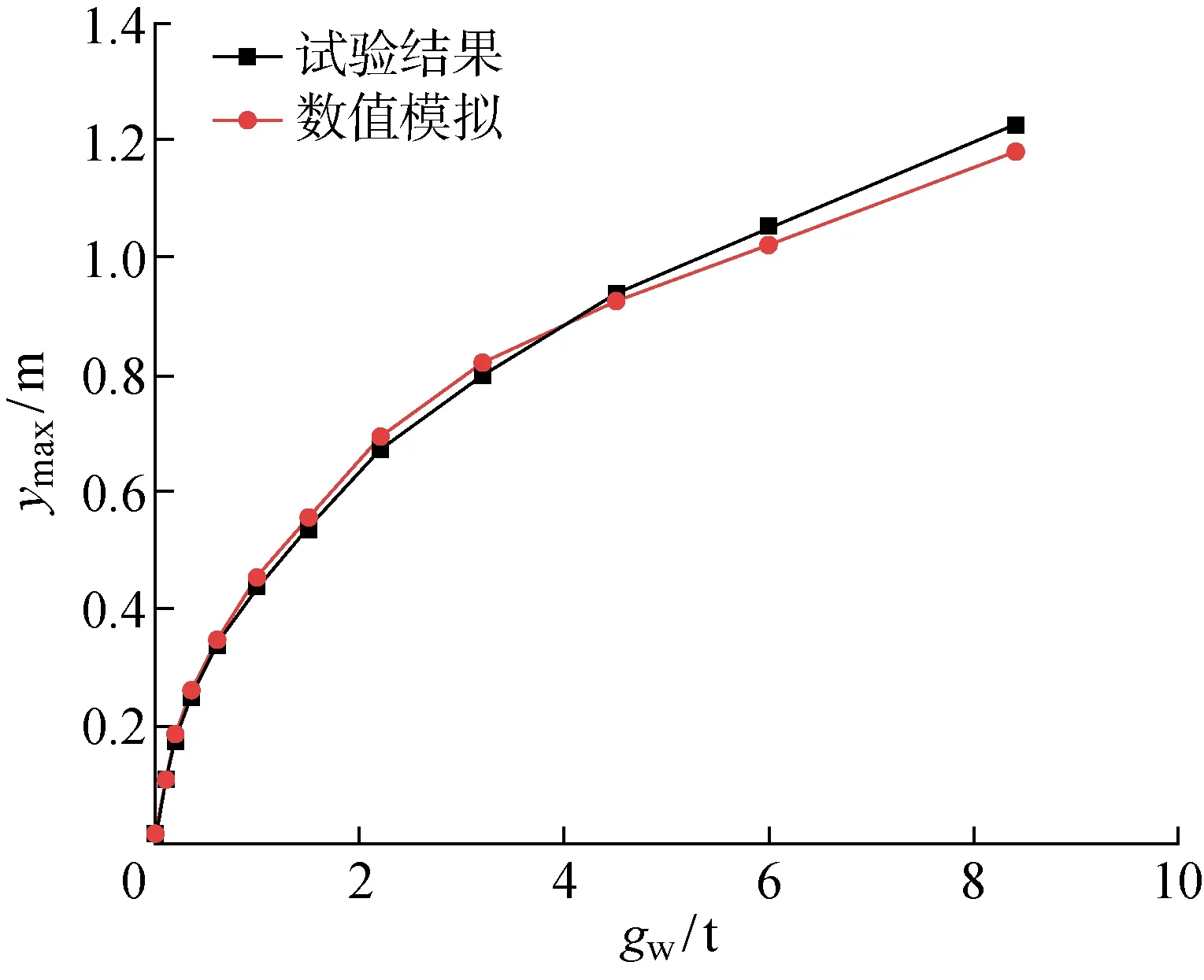
..膜面變形結果分析 圖7所示為8.4 t積水荷載作用下膜面的豎向變形.可以看出數值模擬得到的膜面變形形狀與試驗結果接近，膜面中心的等高線呈圓形，隨著等高線的增高逐漸發展為方形.圖8所示為各級荷載作用下膜面的最大豎向變形與積水荷載的關系曲線，將數值模擬結果與試驗結果進行對比.結果表明，膜面的最大豎向變形在加載過程中呈現明顯的非線性變化.積水荷載小于4 t時，數值模擬得到的變形略大于試驗結果；積水荷載大于4 t時，數值模擬得到的變形略小于試驗結果.積水荷載為0.2 t時，膜面的最大豎向變形的相對誤差最大，為6.8%.積水荷載為8.4 t時，最大變形的差值最大，為0.047 m，此時膜面的最大豎向變形約為1.2 m，最大矢跨比(豎向變形與膜面邊長的比)為2/15，大于一般膜面的撓度限值1/15.因此，膜面積水的過程為顯著大變形過程.將膜面的最大豎向變形與積水荷載的關系進行曲線擬合，可得

垂直搜索引擎當中的一項重要組成部分為爬蟲設計。在爬行器的模塊設計的當中，采用動態化隧道穿越算法的方式，可以確保系統內部能夠獲取更好的UI。在對Web網絡頁面進行設計和布局規劃時，工作人員可以通過應用中間區域存放的方式，采用主題塊和四周導航和廣告的模式，提高用戶對于各項信息和內容的調取效率。例如，我國某高校教學資源庫平臺系統實現環節中，工作人員通過對用戶的操作特征和瀏覽需求進行動態化分析，明確地了解到了普通用戶在瀏覽頁面時，基本上都會將自己的注意力集中在頁面中間的大塊主題區域之中。隨著用戶瀏覽需求的增加，在不滿足于主題區域當中的信息內容時，用戶還可以通過頁面上方和導航欄進行查詢。

=1412-024e-0339-114e-509

(7)

3.2 膜面應力和應變分布

在Abaqus有限元軟件中，建立邊長為9 m的膜面分析模型，四邊鉸接，并在經緯向分別施加 3.1 kN/m 和3.5 kN/m的預應力(結合經緯向應力比為1∶1時的膜材雙軸拉伸試驗，由膜材的裁剪尺寸計算所得)，在膜面中央正上方設置圓柱形水柱，將水和膜面之間的法向接觸設置為硬接觸，切向接觸設置為光滑，有限元模型如圖2所示.在重力作用下，水與膜接觸，加載過程中膜影響水的形狀，水使膜變形.

2.2 GRIM-19基因對HeLa細胞的增殖作用 低表達GRIM-19基因后，HeLa細胞的增殖活力顯著降低(圖2)。運用Western blot實驗檢測低表達GRIM-19基因的HeLa細胞與未處理組抗凋亡相關蛋白P53的改變，結果提示，GRIM-19基因低表達后，HeLa細胞凋亡相關蛋白P53也受到抑制(圖3)，提示GRIM-19基因低表達后促進了HeLa細胞凋亡的發生。

(8)

從圖10中可以看出，隨著積水荷載的增加，最大主應變及最大經緯向應變逐漸增大，由0增加到3.8%左右，且最大主應變曲線與最大緯向應變曲線重合，緯向應變始終大于經向應變，兩者的差值由0增加到0.1%.

工程建設前期準備工作會影響使用過程中的具體狀況。工程質量是決定工程是否合格的關鍵。農田水利工程對工程質量要求十分嚴格。判定工程建設是否合格一般通過兩個環節，即實際應用與監督管理。實際應用情況多與工程本身或自然因素有關。監督管理一般是針對工程建設過程中材料選擇、工程步驟監控、質量評定等方面。

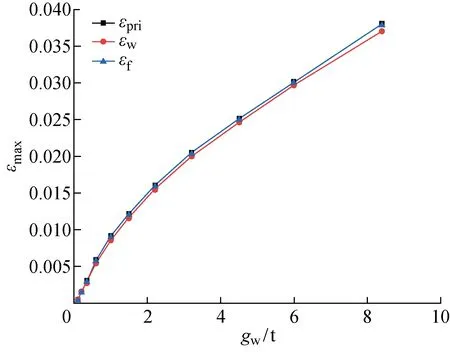
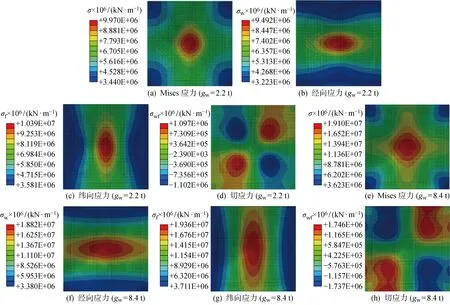
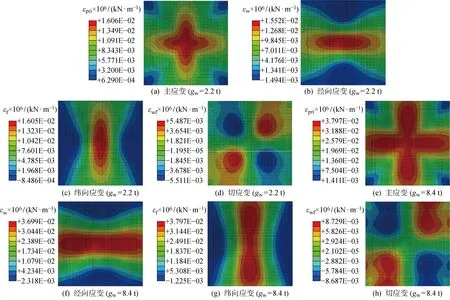
圖11、12分別為2.2 t和8.4 t積水荷載作用下膜面的應力分布和應變分布的數值模擬結果，圖中為Mises應力.可以看出，在加載過程中，膜面高應力和高應變的區域類似，均位于膜面中心與膜面各邊中點的連線上，且具有一定寬度.高應力和高應變區域首先從膜面中心處開始發展，然后逐漸擴展至膜面邊緣中點處，寬度和面積不斷增大.經仔細觀察后發現，膜面經向和緯向的應力和應變分布略有不同，膜面的經緯向的高應力區域的梭形中間區域更寬，兩端更尖，且始終保持梭形.但經緯向高應變區域的兩端尺寸逐漸增大，中間逐漸減小.同時發現切應力和切應變的分布幾乎一樣.以上兩種現象是本文的膜材屬性采用經緯向非線性本構，而切變模量為常量導致的.

4 結論

本文提出一種分析膜面在積水荷載作用下響應的數值模型，結合SPH方法和膜材的非線性本構模型，研究平膜在積水荷載作用下的變形和應力分布，并與試驗結果進行了比較，主要結論有：

(1)根據9個不同經緯向應力比下的雙軸拉伸試驗得到應力-應變響應面，由此計算Jacobian矩陣，并借助Abaqus的UMAT和VUMAT子程序構建了與應力水平相關的膜材非線性本構模型，實現了有限元計算中每一應變增量步的應力和應變的更新.

(2)使用SPH粒子模擬水可以自動考慮水與膜的相互作用，使用平滑分析步的方式使膜面的積水過程更接近準靜態加載.結合SPH方法和膜材的非線性本構對膜面的積水過程進行了分析.通過網格收斂性分析確定了本文采取的網格尺寸；通過不同加載時長的模型分析，得到隨著加載時長的增加，積水的加載過程變得越來越平滑，100 s能滿足分析要求.

(3)由數值模擬與試驗實測結果可以看出，膜面的最大豎向變形呈非線性變化，最大豎向變形約為1.2 m，最大矢跨比為2/15，大于一般膜面的撓度限值1/15.最大豎向變形的相對誤差在6.8%以內，驗證了本文所提方法的準確性和適用性.

以表1所示問題為例，編碼方式如圖2所示，包括機器選擇鏈和工序順序鏈。解碼時，為了盡可能將工序插入到對應機器上最早可行的時刻加工，從而減小最大完工時間，采用主動調度的解碼方式[22]。

(4)膜面的高應力區域和高應變區域均集中在膜面中心與各邊中點的連線區域，膜面應力和應變的最大值出現在膜面中心處，8.4 t積水荷載作用時，膜面最大應力為19 kN/m，最大應變為3.8%.

本文因未進行膜材剪切試驗，所以未考慮膜材的切變模量的非線性，而采用經驗值.這將作為下一步的研究內容.