基于混合摩擦模型的機器人關節摩擦建模與仿真*

董雅文 王鴻飛 張寶鋒 宋栓軍

（①西安工程大學機電工程學院，陜西 西安 710048；②西安理工大學機械與精密儀器工程學院，陜西 西安 710048）

摩擦現象存在于生活中的方方面面，在不同情況下，摩擦發揮的作用不同。在某些情況下，摩擦是有利的，如在路上高速行駛的汽車，正是因為摩擦力車輛才能向前走，在緊急情況下才能剎車。但在多數情況下，沒有摩擦，效果更好，如傳動軸帶動軸承高速轉動時，滾珠和內外圈的摩擦，使整個系統產生穩態誤差，降低了整個系統的運動精度，如果沒有摩擦的影響，傳動精度會更高并且系統壽命會更長。當今，工業機器人技術發展如火如荼，而摩擦是影響機器人關節運動精度的主要原因，尤其在一些對機器人工作精度有一定要求的場合更是如此。對機器人關節準確建模可以提高運動精度和平穩性，并且可以延長連續工作時間和壽命，因此，機器人關節摩擦引起了越來越多專家學者的關注。

為了研究關節摩擦對運動精度的影響，并對機器人進行有效控制，學者們對機器人關節摩擦問題進行了相關研究。Stribeck在1902年提出了Stribeck摩擦模型，LI C B等在1982提出了一個指數模型描述Stribeck現象[1]，該模型描述了低速時的摩擦情況，但缺乏對摩擦動態特性的描述。Dahl Philip R等在1976年提出Dahl摩擦模型[2]，Dahl是最簡單的動態摩擦模型，該模型避免了在靜態狀況下兩階段間切換不連續的問題，但沒有描述低速時的摩擦現象。Armstrong-Helouvry B等在1994年提出七參數模型[3]，該模型描述了摩擦力在不同階段的摩擦，但該模型是一個離散的動態摩擦模型，而且涉及到兩個階段之間轉換不合理的問題，故在具體應用中受到了限制。Canudas-de-Wit C等在1995年提出了LuGre模型[4]，該模型可以描述摩擦力在不同階段的切換，更能符合實際摩擦現象，但由于其參數很難辨識，故在實際應用中受到限制。王毅等建立了一個基于Simulink的仿真摩擦模型，分析摩擦對伺服系統的影響，得到了與理論分析一致的結果[5]。王霞等建立了動態仿真摩擦模型，分析了摩擦力對高精度伺服控制系統的影響[6]。劉麗蘭等系統地介紹了常見的6種靜態摩擦模型和7種動態摩擦模型，并對每種模型進行了詳細的說明[7]。許宏等對Stribeck摩擦模型進行了模糊PID控制，對無刷直流電機控制系統進行了仿真，解決了控制系統在實際運行中存在摩擦負載的問題[8]。徐智浩等建立了一種自適應模糊神經網絡控制器，并建立了動態LuGre摩擦的機械臂模型，解決了由于摩擦非線性導致機械臂控制精度低的問題[9]。朱松青等建立了一個混合摩擦模型來描述關節摩擦問題，以提高機器人動力學建模精度和控制精度[10]。

考慮到單一的摩擦模型不足以解決復雜的關節摩擦問題，從而會影響動力學建模精度，導致控制精度降低。為了更加準確地描述機器人關節內部的摩擦特性，本文采用混合摩擦模型對機械臂關節進行建模，使用MATLAB/Simulink模塊對該摩擦模型進行仿真分析。

1 機器人關節混合摩擦模型建立

機器人關節主要由伺服電機、減速器、力矩傳感器和編碼器組成，其模型如圖1所示。機器人關節作為連接兩機械臂和力矩傳輸的重要部件，相對于其他機械傳動結構，機器人關節的輸出端轉速較低，在一些特殊作業中換向頻繁，并且機器人關節內部結構復雜，摩擦副較多。摩擦對機器人的運動精度、穩定性和可靠性有重要的影響，高速時關節內部的摩擦不太明顯，但在低速高精度的情況下，摩擦的非線性影響較為明顯。可以通過改善機械結構或者對伺服系統進行控制來降低摩擦對系統的影響，但第一種方法由于技術工藝和材料的限制，不容易實現，第二種方法對控制器進行控制，相對第一種方法更經濟有效，但第二種方法需要對關節摩擦進行建模，因此，包含摩擦的關節動力學建模尤為重要。

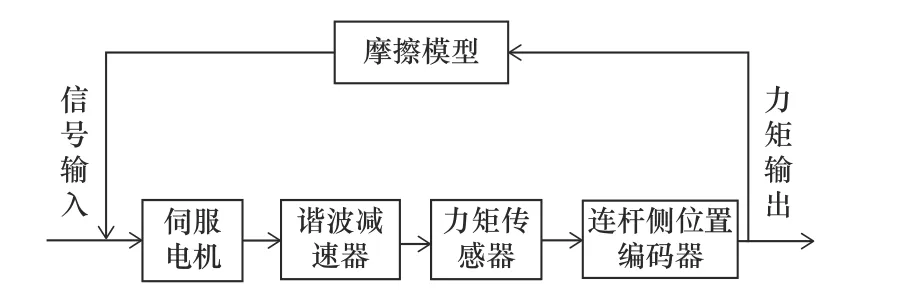
圖1 機器人關節模型

對于機器人關節伺服系統，位置狀態方程表達如下。

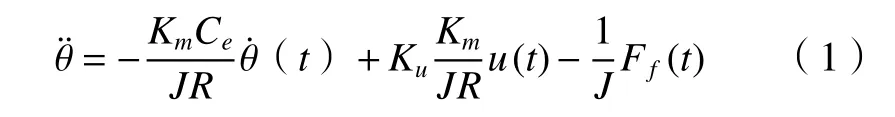
式中：Ff(t)為摩擦項；Ku為功率放大器放大系數；R為電樞電阻；Km為電機力矩系數；Ce為電壓反饋系數；J為電機的轉動慣量；θ˙(t)為轉速；u(t)為控制輸入。

1.1 機器人關節混合摩擦機理

針對機器人關節伺服系統動力學方程的摩擦項為Ff(t)，本文在朱松青等[10]研究成果的基礎上，提出一種基于靜摩擦、庫倫摩擦和Lorentzian模型的機器人關節混合摩擦模型以準確描述關節內的摩擦特性，其中Lorentzian摩擦模型是對Stribeck摩擦模型的改進，包含了粘性摩擦，該模型可以較好地描述機器人關節低速時的摩擦特性，并且可以以90%的準確度來描述關節部位的實際摩擦現象[7]，其混合摩擦模型曲線如圖2所示。

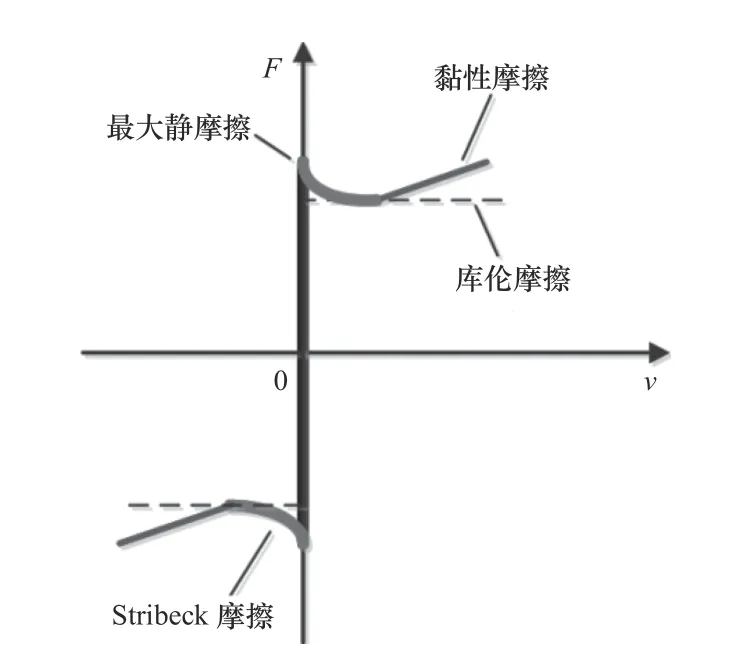
圖2 混合摩擦模型曲線

1.2 機器人關節混合摩擦模型

當機器人關節間有相對轉動趨勢而未轉動時，此時主要為靜摩擦，函數關系式表示如下[7]。

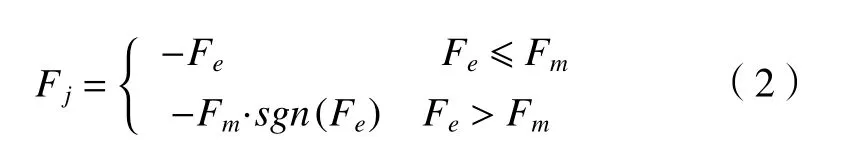
式中：Fj為關節靜摩擦力矩；Fe為外力矩；Fm為最大靜摩擦力矩；sign()為符號函數(Fe>0，sign(Fe)=1；Fe=0，sign(Fe)=0；Fe<0，sign(Fe)=?1)。

當機器人關節低速轉動時，關節內的摩擦主要表現為滑動邊界摩擦，函數關系式表示如下[7]。

式中：Fc為庫倫摩擦力矩；μ為摩擦系數；Fn為法向力矩。

當機器人關節由靜摩擦轉換到滑動摩擦時，摩擦并非是非連續的。摩擦力克服靜摩擦力后不斷下降，在低速時克服摩擦力使其隨著速度的增加而減小，此時摩擦為兩接觸面間相對速度的連續函數，這一現象稱為負斜率摩擦現象。為了充分表達這一轉換過程以及機械臂運行時的黏滯摩擦，可應用Lorentzian摩擦模型[7]。

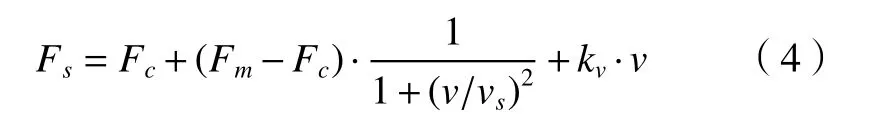
式中：Fs為Stribeck摩擦力矩；kv為黏性摩擦系數；vs為Stribeck速度；v是相對滑動速度。

由式（2）～（4），可得機器人關節的混合摩擦模型如式（5）所示。

從機器人關節摩擦模型關系式可以看出，混合摩擦模型為外力矩Fe、相對速度v和法向力Fn的函數。混合摩擦模型的摩擦曲線如圖2所示，該曲線既表述了摩擦隨速度的穩態運動特性，又體現了摩擦的靜態特性，且通過Stribeck效應更真實地體現了關節在低速段的摩擦特性，提高了關節摩擦建模精度。將式（5）代入式（1）中，可得到含摩擦的關節動力學方程。

2 模型求解和仿真

為了驗證本文建立的基于機器人關節混合摩擦模型的可靠性及準確性，使用MATLAB/Simulink對該混合摩擦模型進行動力學建模仿真[11]，其仿真框圖如圖3所示。

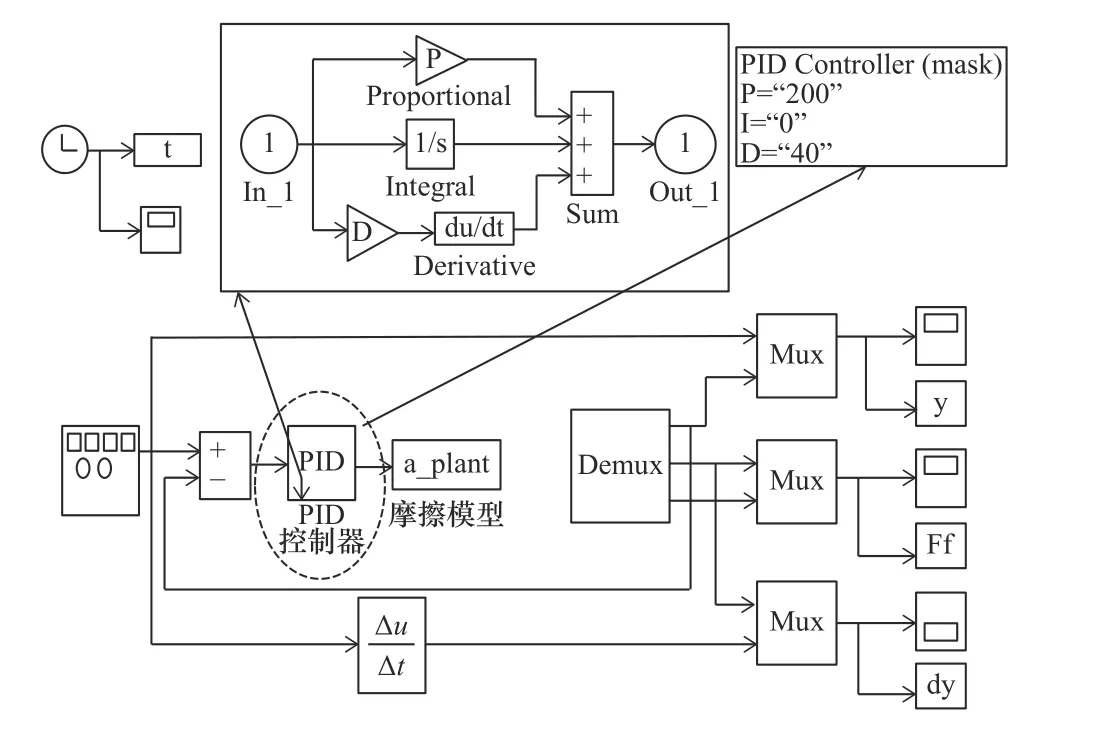
圖3 MATLAB/Simulink仿真框圖

設該仿真系統參數：R=7.77Ω，Km=6N·m/A，Ce=1.2V/(rad/s)，J=0.6kg·m2，Ku=11；摩擦模型參數：取Fc=15N·m，Fm=20N·m，a1=1.0，kv=2.0Nms/rad，Vs=0.05。

低速正弦跟蹤指令信號為y(t)=0.1sin(2πt)，仿真運行時間為3 s，采用PD控制，取Kp=200，Kd=40，機器人關節角速度和摩擦力的仿真結果如圖4所示。

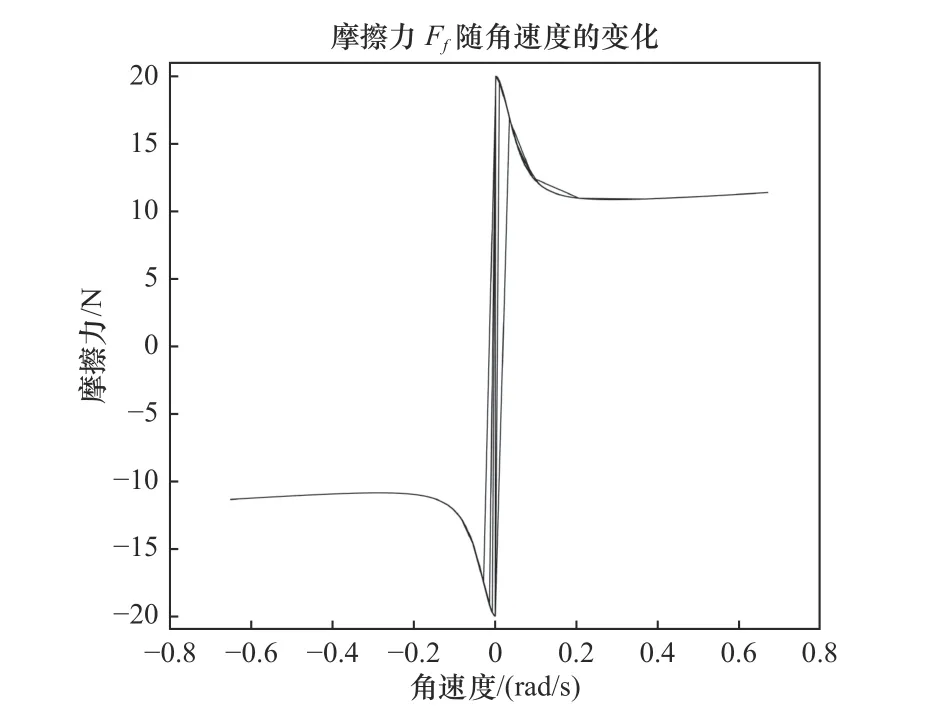
圖4 混合摩擦模型仿真結果

由圖4可以看出，在輸出關節角速度很小時，摩擦力為最大靜摩擦力，此時摩擦力的大小主要與外力Fe大小有關。當角速度在0～0.05 rad/s時，摩擦力由靜摩擦向動摩擦轉換，在兩接觸面剛產生相對運動時，此時為邊界潤滑狀態，由于速度很低，故在兩接觸面間潤滑劑填充不完全，只能依靠邊界部分潤滑以減小磨損。此時為邊界摩擦狀態，并且在低速下隨著速度的增大而減小，為速度的連續函數，這種現象稱為Stribeck現象。隨著速度的增加，部分潤滑劑填充在兩接觸面間，此時為部分流體潤滑階段，由于潤滑劑的黏性，這個階段的摩擦力主要為黏性摩擦。由于該摩擦模型建模過程涉及到符號函數，根據式（5）可得速度變化時摩擦力的變化剛好相反，并且該仿真結果與圖2的結果基本一致，達到了預期的結果。

圖5為關節輸出角位移跟蹤仿真結果，從誤差曲線可以看出誤差隨時間周期性變化，且最大誤差為0.007 1 rad。雖然產生抖動，但無平頂現象，位置偏移小。

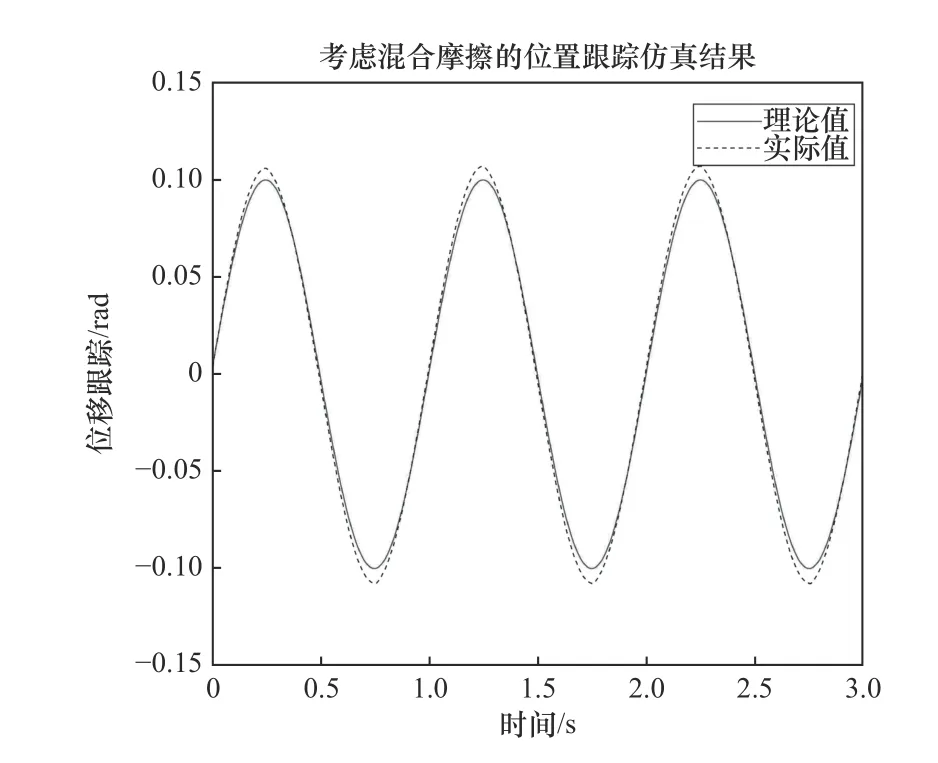
圖5 關節輸出角位移仿真結果

圖6為關節輸出角速度跟蹤仿真結果，從誤差曲線可以看出，在關節由由靜態轉變為動態的過程中，速度會有突變，隨著速度的增加，誤差變化趨于平穩，精度較高。

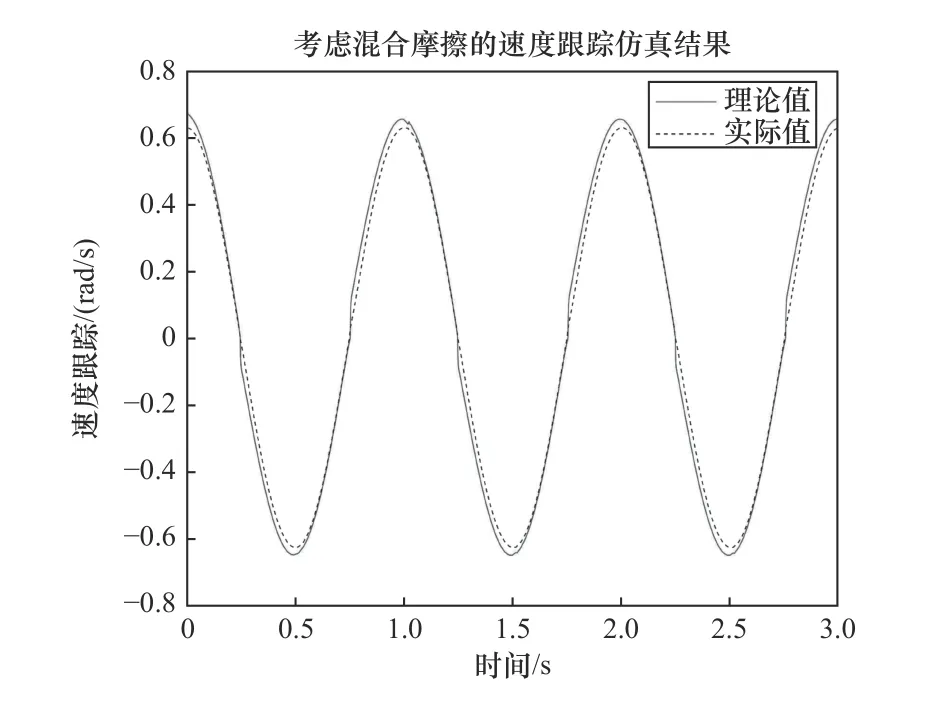
圖6 關節輸出角速度仿真結果

圖7和圖8為3種常用的工業機器人摩擦模型對比分析，各個模型伺服參數的選取與混合摩擦模型相同，選取仿真穩定狀態時的結果進行對比分析。圖7中混合摩擦模型輸出角位移誤差范圍在?0.007 1～0.007 1 rad，LuGre摩擦模型輸出角位移誤差范圍在?0.013 1～0.013 1 rad，Stribeck摩擦模型輸出角位移誤差范圍在?0.012 9～0 rad。從數據結果可以看出，在參數設置相同的情況下，混合摩擦模型的精度要比其他兩種常用模型的精度高一個數量級。

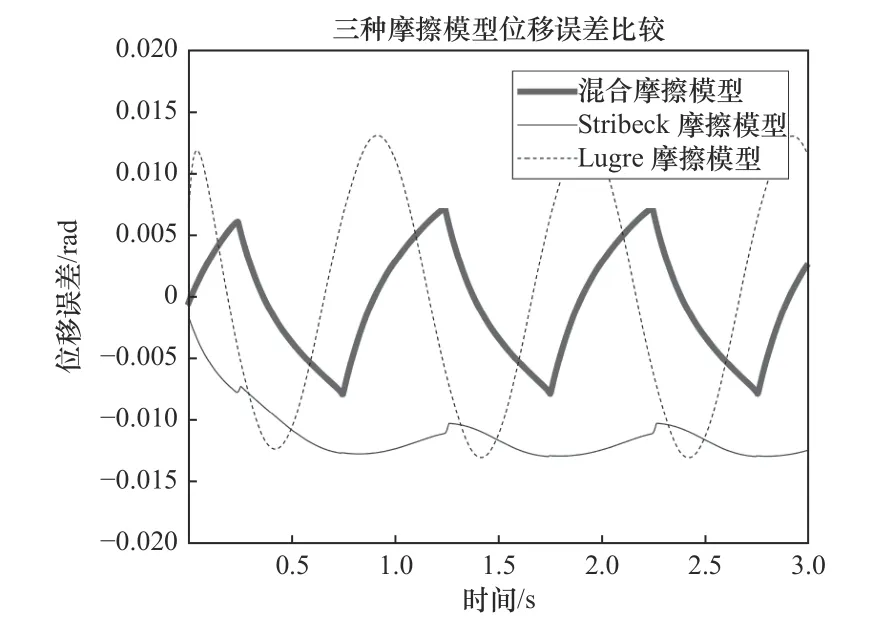
圖7 三種摩擦模型位移誤差比較

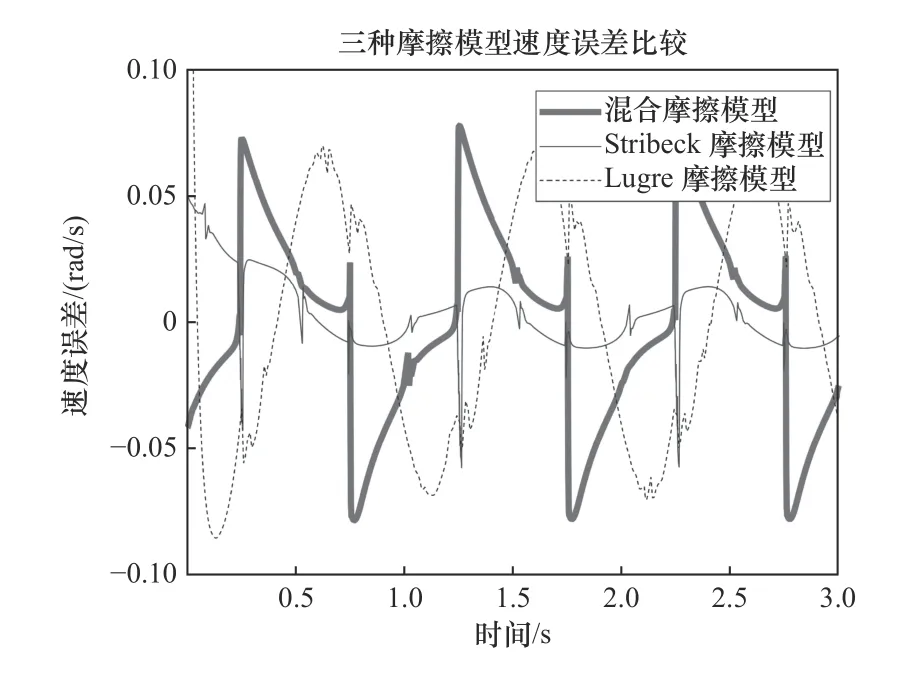
圖8 三種摩擦模型速度誤差比較

圖8中混合摩擦模型角速度誤差范圍在?0.073 1～0.073 1 rad/s，LuGre摩擦模型角速度誤差范圍在?0.070 2～0.071 1 rad/s，Stribeck摩擦模型角速度誤差范圍在?0.070 2～0.071 0 rad/s。仿真結果表明，混合摩擦模型在加速減速切換時會有突變，其余時刻較為平穩，故不適用于需要經常切換速度的場合。

3 結語

本文提出一種基于靜摩擦、庫倫摩擦和Lorentzian摩擦混合表達的混合摩擦模型，建立了包含摩擦的關節動力學模型，使用MATLAB/Simulink進行仿真，并對仿真結果進行對比分析。結果表明，仿真系統參數及控制器參數不變的情況下，取仿真穩定運行的結果，機器人關節輸出角位移誤差為?0.007 1～0.007 1 rad，關節輸出角速度誤差相對比較穩定。由于混合摩擦模型能夠較為準確地表達機器人關節內部實際的摩擦問題，并且，該混合摩擦模型中Lorentzian摩擦模型是對Stribeck摩擦模型的優化，因此，該模型精度比其他模型更高，仿真結果還表明該模型適用于不經常切換速度的場合。