基于等級鄰域策略的偏序柔性車間優化調度*

李長云 林 多 何頻捷 谷鵬飛

（①湖南工業大學計算機學院，湖南 株洲 412007；②湖南工業大學軌道交通學院，湖南 株洲 412007）

柔性作業車間調度問題[1](flexible job shop scheduling problem，FJSP)是一種研究生產資源的分配與工件工序的加工順序的問題，具有加工設備不確定和工藝路線柔性等特性。在實際的車間生產環境中，很多工件的工藝流程具有偏序關系，可能會包含工序具有共同前繼工序或者多個前繼工序的情況，以服裝生產車間為例[2]，在布料裁剪階段之后可以由不同機器并行完成服裝不同部位的縫制，最后再統一進行拼接和后續操作。提高工序的并行性并考慮前繼工序的約束性，能夠實現具有偏序工藝流程的柔性車間調度，提高工廠資源的利用效率。

國內外學者對FJSP的研究主要集中在機器柔性和順序工藝流程的問題，對具有復雜偏序關系的FJSP研究較少。其中，謝志強等[3?4]針對串行工序的緊密度和并行工序的并行性提出考慮后續工序的擇時綜合調度算法。唐紅濤等[5]針對包含并行工序集的車間提出動態觸發鄰域機制增強算法的局部搜索能力。劉曉平等[6]提出了工序和設備分段編碼從而實現適應工件工序可并行的解碼算法，縮短了最大完工時間。徐本柱等[7]研究了工序的并行特性，有效地縮短了產品完工時間。以上算法大都對復雜的并行工序情況考慮不全面，沒有有效地解決串行工序的緊湊度和并行工序的并行性之間的關系，同時未考慮瓶頸工單和瓶頸機器中工件的偏序關系對最小化完工時間的影響。

本文針對偏序柔性作業車間調度問題(partial order flexible job-shop scheduling problem，POFJSP)提出了改進的算術優化算法(improved arithmetic optimization algorithm,IAOA)，設計了基于適應度和工序完工差異度的二維聚類交叉和有效變異策略，并引入一種等級鄰域變異策略對瓶頸工單和瓶頸機器上的工序分等級進行變異，有效地縮短了具有偏序關系工件的最大完工時間。最后通過仿真實驗對比其他優化算法驗證本文所提算法的可行性和優越性。

1 問題模型描述和約束建立

1.1 偏序柔性車間調度問題描述

FJSP中工件工序按照順序關系調度[8]，每個工序在加工機器集中選擇一個機器進行生產。服裝車間中工件的生產需要經過多個工序的加工，每個工序可由一個或多個機器進行加工，每個工序存在一個或多個前繼工序。因此服裝車間的調度問題和FJSP比較類似，但是需要考慮工件加工具有復雜偏序工藝流程的特點。故將服裝車間的調度問題抽象為POFJSP，該問題是FJSP的衍生，針對工件的生產工藝流程通常不是順序型工藝流程，而是具有偏序關系的生產加工關系調度進行研究。

該問題可以采用如下描述：每臺機器完成不同的工單工序所花費的時間不同，每個工單加工產品的工藝流程不同，假設共有n個工單Job={J1,J2,J3,···,Jn}，每個工單Ji(1≤i≤n)包含pi個工序O={Oi1,Oi2,Oi3,···,Oip}，工單工序可以在m個機器M={M1,M2,M3,···,Mm}上進行生產，若工單工序在某些機器Mk(1≤k≤m)上不能生產，則對應的生產時間為空。一個工件的工序可能具有一個或多個前繼工序以及后繼工序，工序Oij具有前繼工序集Fij和后繼工序集Sij。工序的加工時間要介于前繼工序與后繼工序之間，并具有嚴格的加工次序約束。

工件工藝流程如圖1所示，工件J1的工藝流程中工序O12,O13,O14擁有共同的前繼工序O11，工序O11的后繼工序集S11={O12,O13,O14}可并行加工；工序O26有多個前繼工序O24,O25，其最早開始時間為前繼工序集F26={O24,O25}中結束時間ET24,ET25較晚的值。

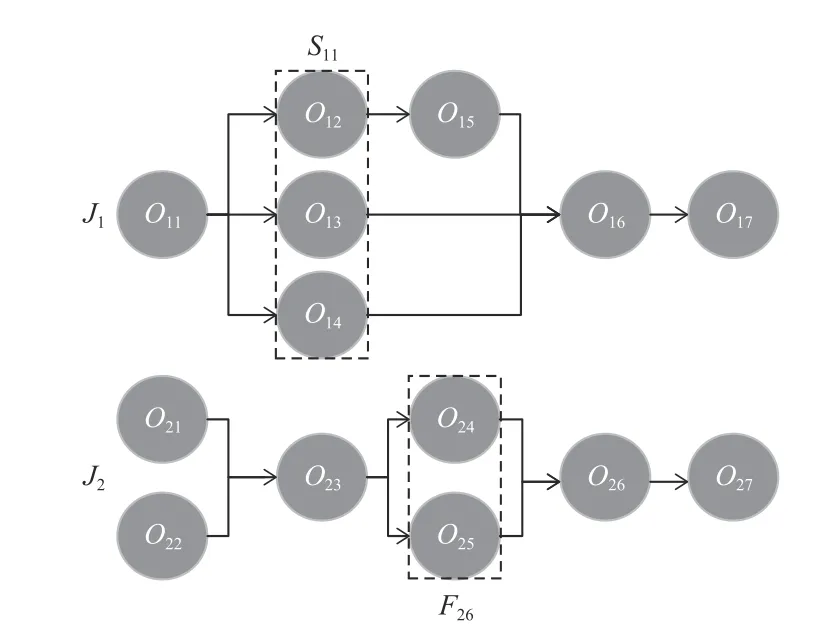
圖1 工件工藝流程圖

1.2 數學模型建立

針對偏序柔性車間調度問題，本文基于以下假設建立數學模型：

（1）零時刻可加工所有工件的第一個工序，且所有機器屬于待工狀態。

（2）一臺機器上不能同時加工多個工序。

（3）同一個工件的前繼工序全部加工完成后才能開始下一道工序。

（4）某工件一旦在某機器上開始加工，不可中斷當前工序的運作。

（5）工件加工互不影響，機器加工互不影響。

為了后續描述表達方便，現將各變量定義如表1所示。

表1 符號及其描述

本文研究的優化目標為最小化機器最大完工時間[9]，基于上述假設條件和數學符號描述模型約束

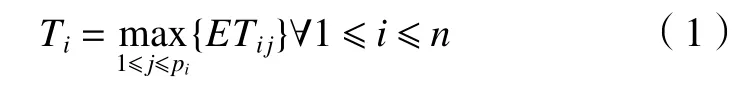
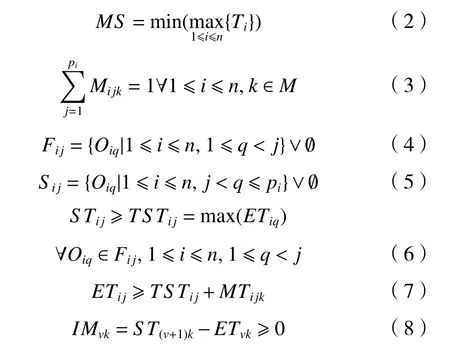
其中：式（1）表示工件Ji（1≤i≤n）的最大完工時間；式（2）表示優化目標為最小化機器最大完工時間，即適應度；式（3）表示工件的每道工序只能在一臺機器上加工；式（4）表示工件工序含有一個或者多個前繼工序，規定工單開始工序的前繼工序為空；式（5）表示工件的結束工序不包含后繼工序（置為空集），其他工序的后繼工序集中包含一個或多個工序；式（6）表示需要完成當前工單工序的全部前繼工序后才開始加工；式（7）表示Oij的最早結束時間為其前繼工序的完成時間的最大值與其所在加工機器上的加工時間之和；式（8）表示機器加工當前工序完成之后才能開始下一個工序的加工。

2 基于等級鄰域策略的改進算術優化算法（IAOA+GNS）設計

算術優化算法(arithmetic optimization algorithm,AOA)[10]是一種群智能算法，用于解決連續型運籌優化問題，具有調整參數少，收斂速度快等優點，其思想適用于解決偏序柔性車間調度問題。在原始的AOA中，將其分為兩個主要階段：勘探和開發。在勘探階段算法先對搜索空間進行廣泛覆蓋搜索，以避免陷入局部解，開發階段對勘探階段得到的解進行鄰域搜索，算法步驟如下。

Step1：設定種群迭代次數T，種群大小popsize，隨機初始化生成一組候選解X(1)。首先解碼根據式（2）計算種群適應度MS，并將當代種群的最佳候選解視為目前獲得的最佳解Xbest(t)，然后通過式（9）計算MOA(t)進行階段選擇。MOA(t)為選擇概率，Min為最小概率，Max為最大概率，本文設定Min=0.2，Max=1，隨著迭代次數的增加，選擇開發階段概率逐漸大于勘探階段。

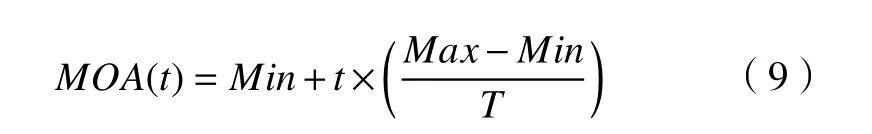
Step2：勘探階段，在Xbest(t)附近使用搜索策略在多個解空間上進行隨機搜索，從而擴大種群多樣性。

Step3：開發階段，利用搜索策略在適應度值較高的解鄰域進行深入搜索，并在經過多次迭代之后發現接近最優的解。

AOA算法主要用于求解連續型問題，本文研究的POFJSP屬于離散型問題，因此提出一種基于偏序工序的改進算術優化算法（IAOA），其次在勘探階段設計了基于適應度和工序完工差異度的二維聚類交叉和有效并行變異策略增加種群多樣性，在開發階段設計了一種等級鄰域搜索（grade neighborhood search，GNS）策略增強算法的局部搜索能力。最后結合兩者提出基于等級鄰域策略的改進算術優化算法（IAOA+GNS）求解POFJSP。

基于等級鄰域變異策略的改進算術優化算法流程如圖2所示。

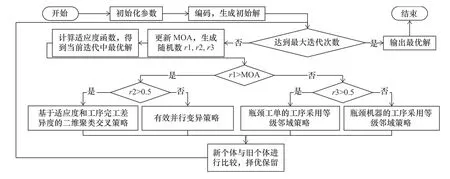
圖2 IAOA+GNS算法流程圖

2.1 編碼解碼

POFJSP需要考慮到工件工序以及生產機器的安排，本文采取雙編碼形式Xi(t)=[Xg|Xm]對工序和機器進行編碼，Xg為工序編碼部分，工件Ji出現的次數為其第j個工序，Xm為機器編碼部分，表示對應工序Oij的可選機器集中的機器編號Mijk。編碼形式如圖3所示。

圖3 編碼示例圖

解碼是群智能算法能否解決車間調度問題的關鍵，考慮解碼的多約束性并通過工件前繼工序和機器可用時間段可以確定后繼工序的最優加工時間，IAOA進行解碼時具有以下步驟：

Step1：將候選解Xi(t)的工序編碼部分換算為工件工序Oij列表，找到對應的安排機器Mijk。

Step2：將前繼工序為空集的工序的最早可開始時間TSTij初始化為0，其他的工序則按照式（6）計算其TSTij。

Step3：對Oij使用基于插入優先的解碼策略：當Oij安排的Mijk上已安排的工序數大于0時，轉到Step3.1，否則轉到Step3.3。

Step3.1：判斷Oij能否插入到Mijk上的第一個工序前，如果第一個工序的開始時間STM1k大于等于Oij的TSTij和其加工時間MTijk之和，則跳轉到Step4，否則判斷Mijk上已安排的工序數是否大于1，是則跳到Step3.2，否則跳到Step3.3。

Step3.2：循環安排在Mijk上，且時間在Oij的TSTij之后的所有工序OMvk，使用式（8）計算兩個工序之間的時間間隔IMvk，在Oij的TSTij和工序OMvk的結束時間ETMvk中選擇較大的值，判斷該值和Oij的加工時間MTijk之和是否小于下一個工序的開始時間STM(v+1)k，并且IMvk是否大于等于Oij的MTijk，是則表示可以插入該空閑時間段，轉到Step4。循環完畢，如發現沒有可插入的時間段，則跳轉到Step3.3。

Step3.3：Oij不能插入Mijk上的空閑時間段，在Oij的TSTij和Mijk上已安排的最后一道工序的結束時間ETMvk中選擇較大的值，該值即為Oij的真正開始時間STij。

Step4：利用式（1）和式（2）算出目標函數值。

如圖4所示，有3個具有偏序關系的工件，將部分工序按照解碼步驟解碼到調度甘特圖，以工序O22為例，其TSTij=3，機器M1安排工序數大于2，轉到Step3.2檢查空位1發現IM12≥MT221但MT221+TST22≤STM21，檢查空位2發現IM22≥MT221且ETM21+MT221≤STM31，符合條件，可插入空位2。

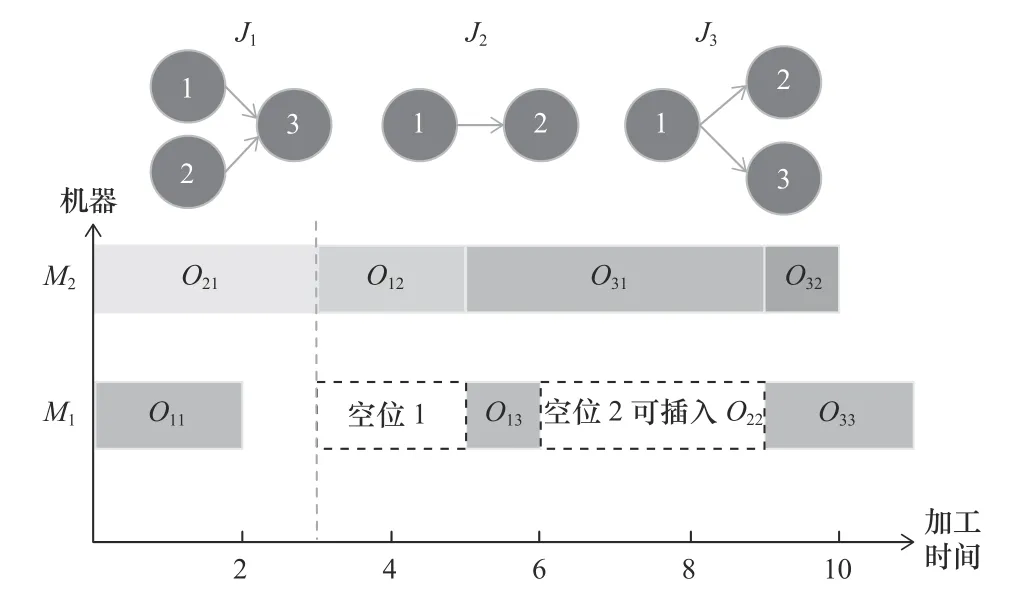
圖4 解碼調度甘特圖

2.2 種群初始化

種群初始化的質量好壞直接影響到算法求解速度和最終解的質量，為了減少無效解的產生并增加種群多樣性，采用以下兩種方法進行種群初始化（兩種方法生成的初始解在初始種群數量中各占50%）。

正向法：首先隨機打亂工序編碼，并為每道工序隨機分配機器，隨后通過前繼工序表查看所有工序，將具有共同前繼工序的工序編碼排在一起，最后檢查同一工單中具有共同前繼工序的工序的機器編碼，如果在同一臺機器上加工，則在可選機器集中重新選擇機器進行分配。

逆向法：由正向法生成的工件編碼通過倒置得到逆向編碼，機器編碼仍采用正向法編碼規則隨機生成。

2.3 勘探階段

IAOA算法在傳統AOA算法上融合了GA算法的思想，將搜索策略替換成了交叉和變異，以此解決離散調度問題，因此在勘探階段中使用二維聚類交叉策略和有效并行變異策略擴大種群多樣性。

2.3.1 二維聚類交叉策略

本文使用聚類交叉方法進行操作，由于不同適應度值的兩類個體基因存在相似可能性，因此對種群內每個個體引入工序完工差異度（degree of variance of process completion,DVPCs），DVPCs可以計算出不同個體基因之間的差異度，結合適應度值組成二維聚類再進行交叉增大種群多樣性。工序完工差異度計算式（10）如下。

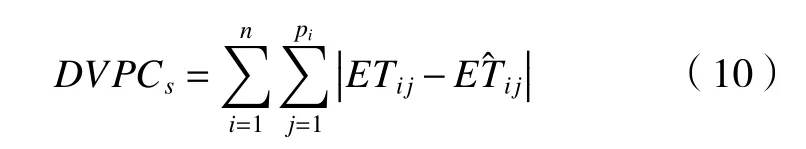
首先以當前迭代種群最優個體Xbest作為基準，對種群中所有個體的適應度MSs和DVPCs統一進行最大最小歸一化，范圍為[0,1]，并以MSs和DVPCs作為指標繪制散點圖。隨后使用k-means聚類算法對種群進行二維聚類，其中參數k為聚類的數量，本文將k設為4，對應不同MSs和DVPCs下的個體類，聚類算法結果如圖5所示。

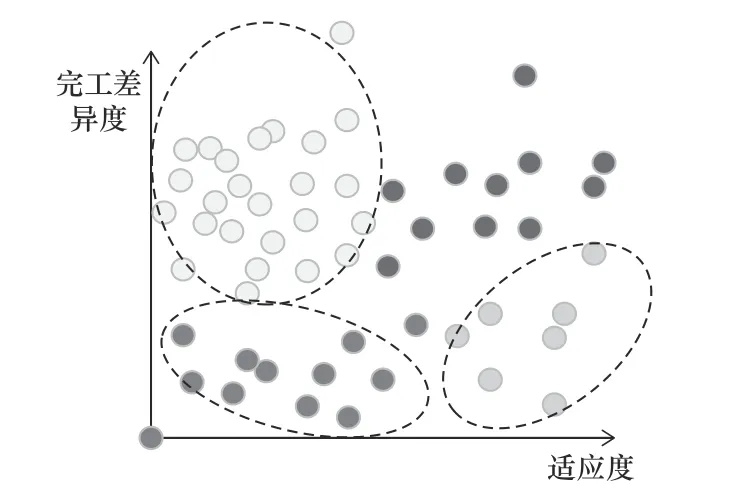
圖5 適應度和完工差異度聚類圖

隨后隨機選擇兩類中的個體作為父代，保留其中適應度較小的父代中的優秀基因，優秀基因為個體基因中工單緊湊度（work order compactness，WOC）高的工單，WOC可通過比較工單理想完成時間和工單實際完成時間獲得，如式（11）所示。

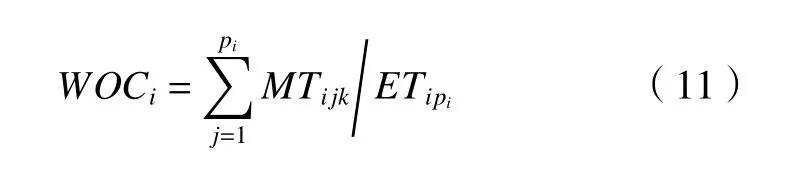
優秀基因的保留能夠加快迭代速度并優化子代基因以獲取更優解。最后使用POX交叉將父代P1的優秀基因保留，其他基因刪除，并將另一父代P2中除了優秀基因工單外的其他工單從左到右依次填補到P1的空基因位上得到交叉后的子代基因。

2.3.2 有效并行變異策略

針對變異過程中可能存在的無效變異問題，本文對機器變異和工序變異進行了以下改進。

機器變異：隨機選擇總數量中20%的工序，將其對應機器換成可選機器集中加工時間更短的機器進行加工。

工序變異：針對不同機器上的工序進行位置交換可能對該機器的加工工序數量和順序不具有任何影響，從而導致無效變異的問題。本文對同一臺機器上加工的任意多個工序交換位置，可有效減少無效變異。

2.4 開發階段

影響適應度函數的直觀原因在于以下兩點：一是瓶頸工單的WOC在所有工單的WOC中處于較低值，大部分工序在對應機器上的加工時間比較長，且與前繼工序之間的時間間隔較大；二是瓶頸機器上的利用率遠高于其他機器，瓶頸機器上加工的工序將對目標函數值起到決定作用。

基于上述問題，開發階段在多個密集解空間上深入搜索最優解，使用等級鄰域搜索策略（GNS）分別對瓶頸工單和瓶頸機器兩個方面進行鄰域搜索。GNS策略如下：

（1）優先級設定。首先為不同情況下的工序設定優先等級，具有多個后繼工序的工序在機器上的完成時間能夠影響到所有后繼并行工序的完成進度，是縮短工單的最大完工時間的重要因素，因此該類工序為最高優先級G1；多數工序只存在一個后繼工序，可以通過對該類工序使用優化策略縮小目標函數值，因此設為中等優先級G2；最后一道工序對整個工單的完成時間影響不大，設為最低優先級G3。

（2）變異策略設定。針對不同原因對工序進行不同的變異策略，分為以下3種情況討論。

GNS1：如果當前工序的開始時間和前繼工序的完成時間間隔大于當前工序加工時間的一半，則將當前工序與對應機器上其前繼工序完成時間之后開始加工的其他工序隨機進行位置互換；

GNS2：如果當前工序與前繼工序的時間間隔較小，則將當前工序換到可選機器集中加工時間更少的機器；

GNS3：如果當前工序所處機器上沒有空閑時間段，則將當前工序交換至可選機器集中機器負載更小的機器上。

若同時滿足多種情況，則隨機選擇一種情況進行變異。

（3）瓶頸工單或瓶頸機器變異。對瓶頸工單或瓶頸機器中的所有工序進行優先級排序，隨后使用輪盤賭算法按照優先級隨機挑選10%工序，并根據不同情況進行變異。

以圖4所示的解碼調度甘特圖為例，假設在第t次迭代中對瓶頸工件J3進行等級鄰域變異，其中O31的優先級最高有多個后繼工序S31={O32,O33}，使用GNS3策略選擇可選機器集中負載更低的機器M1進行加工，得到的調度甘特圖如圖6所示，有效地提前了工件J3的部分工序加工時間。

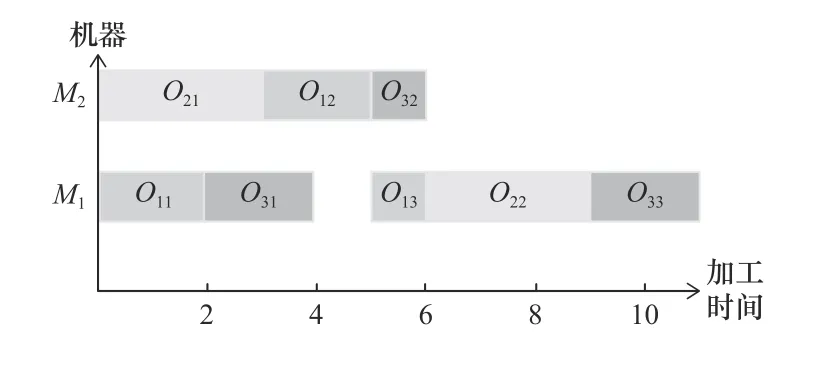
圖6 瓶頸工件使用等級鄰域策略結果圖

假設在第t+1次迭代中對瓶頸機器M1上的加工工序進行等級鄰域變異，采用GNS1策略對工序O22與其前繼工序的完成時間之后開始加工的工序O13進行位置交換，調度甘特圖如圖7所示，最大完工時間從原先的11有效地縮短到10。

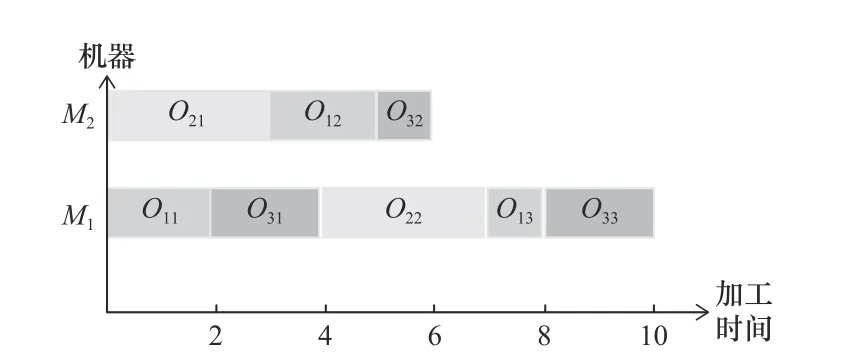
圖7 瓶頸機器使用等級鄰域策略結果圖

3 仿真實驗與案例分析

目前沒有標準算例驗證本文的研究問題，因此本文基于Brandimarte P[11]所提出的10個案例Mk01～Mk10拓展了適用于偏序柔性車間調度問題的測試算例，表2為生成的擴展算例的參數，新算例PMk01～PMk10在基準算例的基礎上添加了每個工序的前繼工序集合，為了表達方便，假設每個算例中工件的工藝流程一樣。

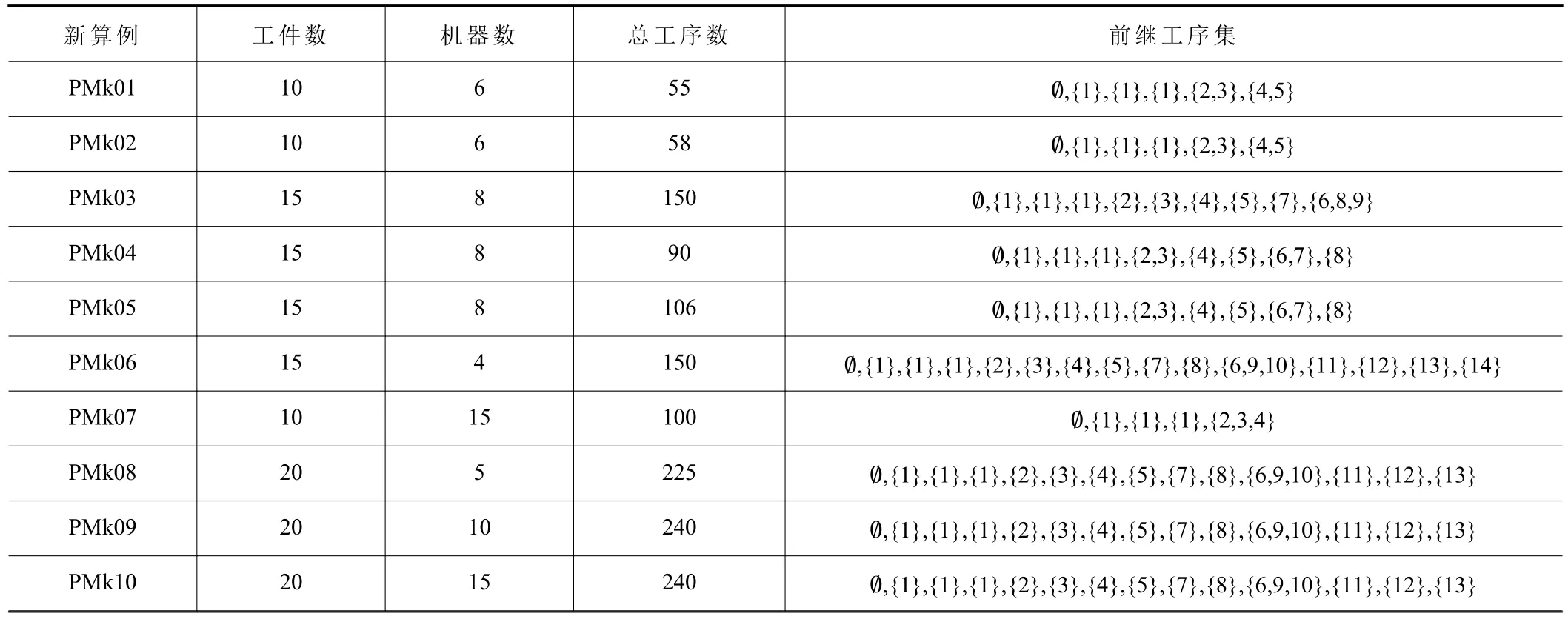
表2 擴展算例參數

3.1 參數對比實驗

智能優化算法的優化結果受算法參數的影響很大，影響算法性能的參數有：種群規模popsize，最大迭代次數T，本文實驗所用算法均采用相同參數值。以PMk09為測試算例，選擇規模為(32)的正交實驗進行測試，為避免結果的隨機性，以30次結果的平均值作為評價指標，正交實驗結果如表3所示。

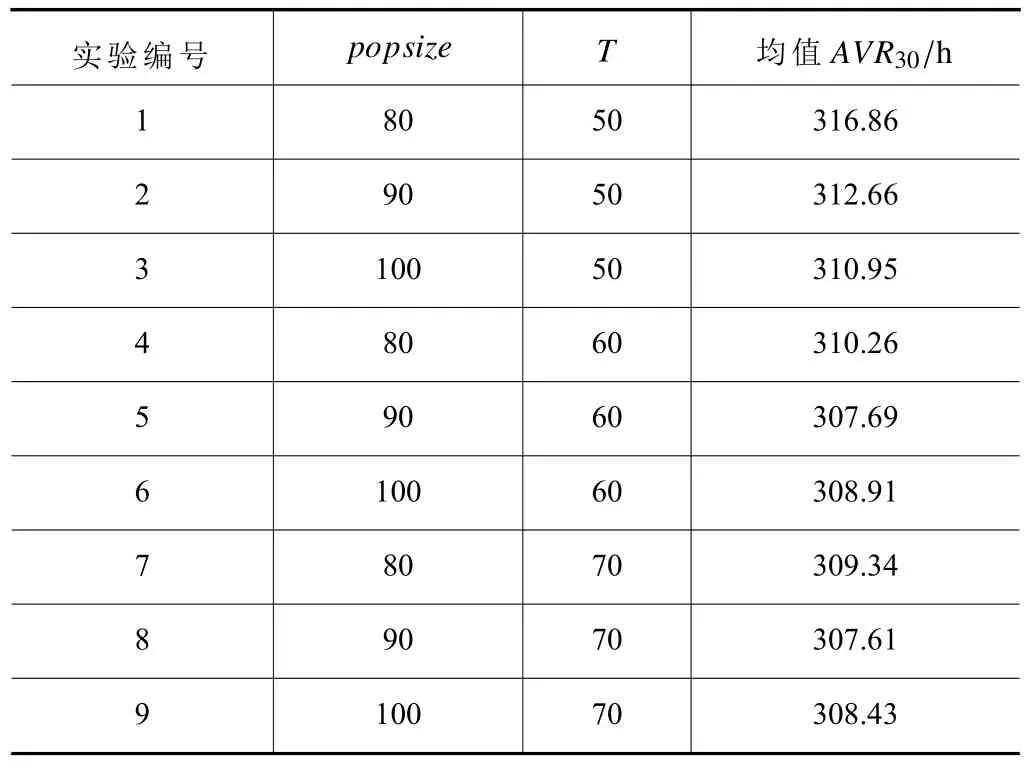
表3 正交實驗結果比較表

可以從表中看出當種群規模popsize=90，最大迭代次數T=70時算法的性能最好，但是當群規模popsize=90，最大迭代次數T=60時算法效果已經接近最優性能，且運行時間少于達到最優性能所花費的時間，所以本文選擇群規模popsize=90，最大迭代次數T=60作為PMk09算例的最優參數。

3.2 算法比較及結果

為了證明本文的IAOA+GNS算法應用在偏序柔性車間調度上的有效性，將本文所采用的方法與文獻[12]和文獻[13]的算法求解效率進行對比，對比算法的參數與本文算法的一致。同時為了驗證本文等級鄰域策略的有效性，選擇與去掉GNS策略采用傳統變鄰域搜索的IAOA+VNS算法進行對比，其中IAOA+VNS算法參數與IAOA+GNS一致。仿真軟件使用MATLAB 2016a，電腦硬件參數為：處理器 Intel(R) Core(TM) i5-4210U CPU @ 3.70 GHz，內存8 GB。算法各運行30次，并使用運行結果中的最小完工時間Rbest、平均完工時間Ravr、完工時間標準差Rσ和算法平均運行時間評測算法性能。

根據表4的仿真結果可以分析出本文的IAOA+GNS算法應用在偏序柔性車間調度具有較好的效果，最小完工時間和平均完工時間均優于其他優化算法，且完工時間標準差少于其他算法，說明本文算法能夠得到更優解，且更穩定性。同時基于IAOA+GNS與IAOA+VNS算法的對比試驗可以說明GNS策略的有效性。

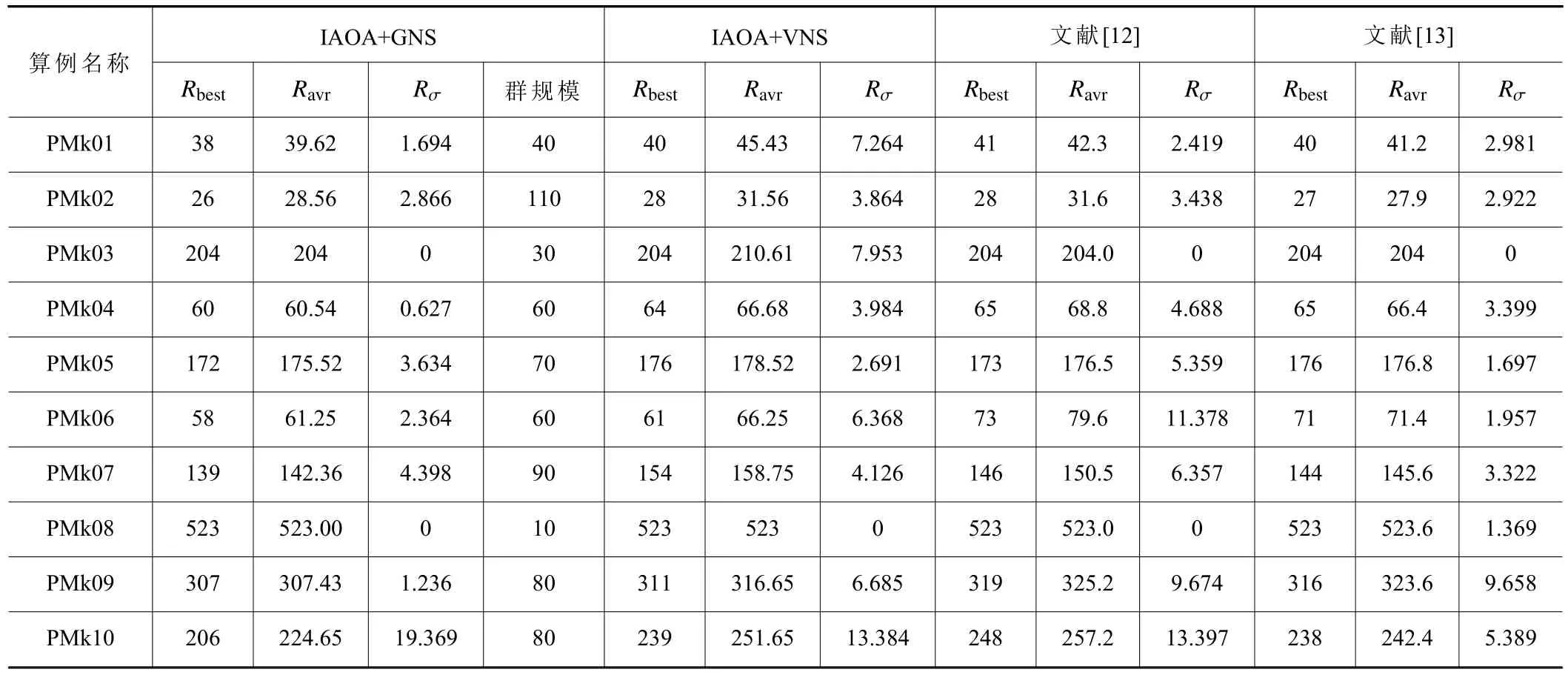
表4 算法效果比較

根據表5的算法平均運行時間來看，算例PMk05、PMk07、PMk09在本文的運行時間比其他算法運行時間更短，最小化最大完工時間也更短。在PMk08算例中大部分工序只能在同一臺機器上進行加工，其適應度函數取決于在此機器上加工的工序完成時間，因此無法體現本文算法的優越性。在其他算例中本文算法比其他優化算法的平均運行時間更長，但是本文算法的運行結果更優，且運行時間在可允許范圍之內。同時，IAOA+VNS算法比IAOA+GNS算法運行時間少很多，但是其算法穩定性相較于較差，體現了本文改進的IAOA+GNS算法在穩定性上的優勢。綜上所述，本文算法在解決偏序柔性車間調度問題上相較于現有其他幾個算法在性能和穩定性上更優越。

表5 算法平均運行時間

以算例PMk09為例，圖8展示了本文算法對該算例的調度甘特圖，從圖中可以看出，其最大完成時間為307，8號機器為瓶頸機器，該機器上已無空閑時間可進行調度，限制了適應度函數的最小值。

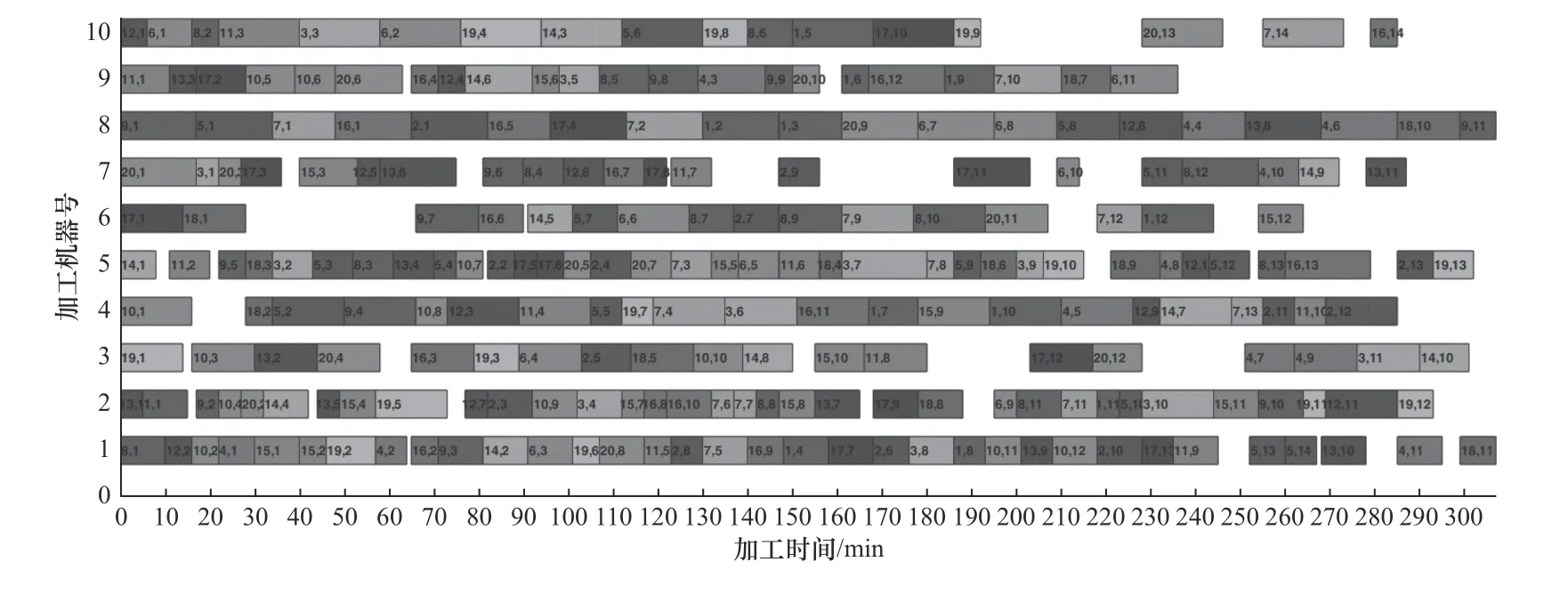
圖8 算例PMK09調度甘特圖

4 結語

針對服裝加工行業中工件具有復雜工藝流程的情況，本文提出了IAOA+GNS算法求解該類偏序柔性車間調度問題。算法充分考慮了前繼工序的約束性，首先基于適應度和工序完工差異度設計出聚類交叉和有效變異策略，避免無效變異的同時擴大了種群探索范圍；然后利用瓶頸機器和瓶頸工件的關鍵性進行等級鄰域變異以搜索更優解。通過仿真實驗對比其他算法，驗證了IAOA+GNS算法的有效性和穩定的求解性能。接下來將下一步的研究重點放到動態調度偏序柔性車間調度上。