雙擺臺五軸磁流變機床結構參數標定方法研究*
曾靖超 伍劍波
(四川大學機械工程學院,四川 成都 610065)
隨著科學技術的不斷發展,對光學系統提出了新的課題與要求,尤其是對于各種復雜曲面光學元件的加工精度、加工效率和輕量化程度等都有了更高的要求。磁流變拋光技術作為一種新的柔性加工方法,依靠一種帶磁性的液體通過外加磁場的作用下,在拋光輪表面形成類似固體的狀態,從而對工件進行拋光[1?2]。在多軸數控機床的控制下,具有良好的確定性加工性能,可以實現復雜曲面光學元件的拋光工作。多軸數控機床加工的位置指令是通過對機床拓撲結構以及各結構參數進行運動學變換得到。標定參數的誤差,將會影響拋光點的軌跡,從而導致拋光確定性下降甚至損壞工件,因此,實現拋光輪結構參數準確標定,對提高磁流變拋光精度有著重要意義[3?7]。
劉杰[8]利用對刀表與球頭棒,記錄各旋轉軸在不同位置下的標定坐標值,計算其偏移矢量,完成標定。鄭飂默[9]使用觸發式測頭對標準球進行數據采集,計算出誤差后,更新機床參數完成標定。上述方法適用銑床類五軸機床,磁流變拋光機床與傳統數控銑床不同的地方在于,銑床可以通過試切法、球桿儀和測頭等方法對刀具進行標定,磁流變拋光頭因磁流變機床由于拋光輪的形狀以及加工方式,需要先確定磁場作用下拋光液形成的緞帶在軸向方向的位置,再確定拋光點徑向位置相對擺軸的距離,無法應用上述方法。
針對磁流變拋光點相對機床轉軸軸線標定問題,常規方法是使用千分表,對刀表與檢棒,通過將檢棒插入并調整至擺軸軸線位置,利用千分表測量其軸線位置,再通過反復移動拋光輪,用千分表尋找拋光輪徑向方向最低點,從而計算相對位置關系,如圖1所示。但是由于磁流變機床AB軸的行程通常小于60°,檢棒與轉軸之間的同心度難以保證,并且需要反復旋轉擺軸調整檢棒,為減小拋光輪圓度輪廓誤差需要多次測量尋找輪心,測量過程較為復雜,耗時較長,最終影響標定精度。

圖1 千分表測量示意圖
本文提出了一種五軸磁流變機床拋光點的結構參數標定方法。完成了機床結構參數標定工作,在此基礎上,開展了預測與驗證實驗,實驗結果證明了標定參數的準確性以及標定方法的實用可行性。
1 測量標定的對象與方法
機床部分結構如圖2所示,拋光輪安裝在B軸擺軸平臺上,B軸平臺與接觸式測頭皆安裝在A軸轉軸支架上。需要標定的拋光輪在機床上的結構參數,分別為機床測頭與機床A軸軸線在Y與Z方向的距離Yma與Zma,拋光輪最低點與機床測頭Y與Z方向的距離Ywm與Zwm,以及拋光輪輪心軸線與B軸軸線在X與Z方向的距離Xwb與Zwb。
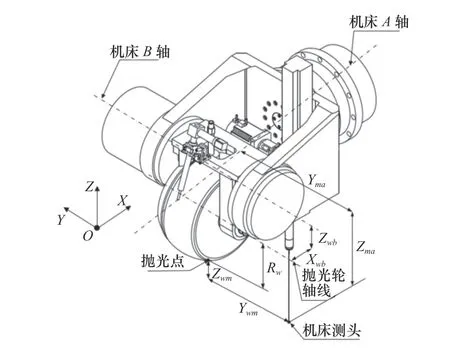
圖2 機床與拋光輪結構示意圖
在標定拋光點與B軸軸線的相對位置關系前,需要確定拋光點在拋光輪軸線方向的位置,因此需要先標定拋光點與A軸的結構參數。由于拋光輪在YOZ面上投影的形狀不是標準的圓形,因此拋光點與A軸的相對位置關系準確標定困難,需要通過標定拋光點與機床測頭、測頭與A軸軸線的位置關系,間接完成標定工作。
1.1 A軸軸線與測頭球心空間關系標定
通過在機床工作臺上固定一個標準方形件,并調整其位姿,使其與機床坐標系方向平行,旋轉機床A、B軸至0°,移動機床,使接觸式測頭測量工件上表面的Z向坐標值Zma0與側表面Y向坐標值Yma0。機床B軸保持0°位置不變,將機床A軸旋轉至θ,測量工件上表面的Z向坐標與側表面Y向坐標,多次旋轉機床A軸至不同角度 θi并測量標準方形工件,記此時機床Y軸坐標值Ymai={Ymai|Ymai,i=1,···,n},Z軸坐標值Zmai={Zmai|Zmai,i=1,···,n},計算A軸在該軸角度下的測量坐標與0°時的測量坐標的相對距離得到A軸軸線的實際位移量ΔYai與ΔZai。
根據當前機床的拓撲結構類型建立數學模型算法,得到測量的位移量ΔYai與ΔZai以及旋轉角度θi的數學關系,如式(1),通過求解式(1)得到機床測頭距機床A軸軸線在Y、Z軸方向上投影的結構參數Ymai與Zmai,求取均值,減小測量誤差帶來的影響,提高標定準確性,如式(2)。
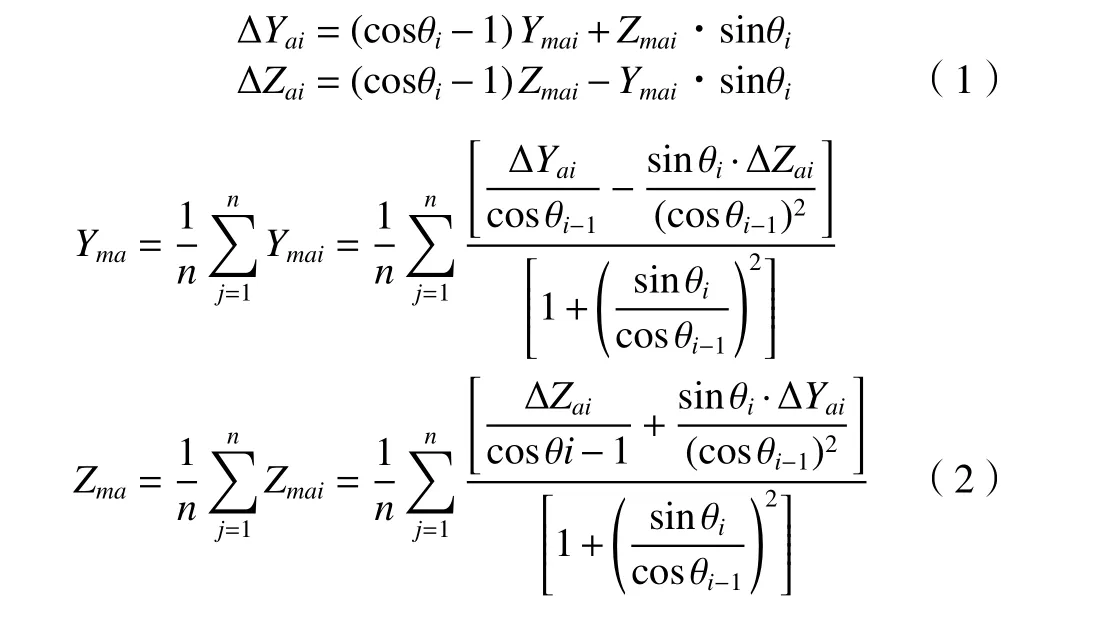
1.2 測頭球心與拋光輪拋光點空間關系標定
由于拋光輪在軸向方向為圓弧狀,隨著軸線方向位置的改變,對應點輪半徑也隨之改變,因此,在測量實際拋光點與機床B軸的相對位置關系前,首先需要確定拋光點在拋光輪軸向方向的位置,由于實際拋光點在拋光輪軸線方向的位置取決于磁流變液在磁場作用下生成的緞帶位置,因此要準確標定機床拋光點在拋光輪軸向的位置,可以通過機床上的接觸式測頭對方形工件進行對刀獲得測頭環境下的工件中心的位置信息,將粗標定獲取的拋光點與測頭的相對位置關系補償進去,并且針對該位置采1組平行斑。通過激光干涉儀測量平行斑各自的峰值點找到兩斑之間的中心位置[10],將該位置與工件中心對比,將該偏移量補充進粗標定中的測頭與拋光點的相對距離中,即可得到拋光點在拋光輪軸線方向上的實際位置,如圖3所示。
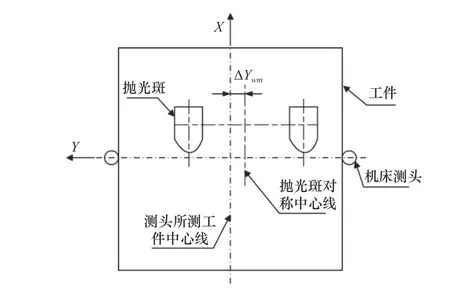
圖3 拋光點軸向位置標定示意圖
粗標定中可以得到拋光輪與測頭在Y方向的大致距離Ywm0,根據采斑得到測頭測量的實際工件中心與拋光點建立的工件中心坐標之差ΔYwm,將其補償,得到準確的結構參數,如式(3)。
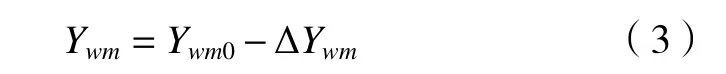
拋光點與測頭的Z向相對距離Zwm可以通過機床測頭與工件直接獲取,根據式(1)~(3),可得到拋光輪最低點與機床A軸軸線的相對位置關系,如式(4)。

1.3 B軸軸線與拋光輪空間關系標定
千分表的測量桿軸線與被測工件表面的夾角愈大,誤差就愈大,此外若磁流變機床磁場部件采用永磁結構,產生的強磁場會影響千分表的測量精度,激光位移傳感器作為高精度的非接觸測量手段,測量過程無需與待測工件接觸,不易受到環境干擾,采用非接觸式測量的方式無疑會降低測量誤差,提升標定精度[11?15]。
根據前面的方法獲取拋光點在拋光輪上的軸向方向(Y方向)位置后,即可移動傳感器測點至該位置,并調整機床的X方向使用傳感器測量拋光輪表面最低點位置,在傳感器中將該點位置置零。為減小拋光輪圓度輪廓誤差帶來的測量影響,采用旋轉拋光輪的方式,分別尋找拋光輪在X、Z方向上均值最低點的位置,將該點作為測量參考點,記錄此時的機床坐標。轉動B軸,在多次測量不同角度下的拋光輪最低點的位置參數后,根據幾何關系,解算拋光輪與B軸軸線的結構參數,完成標定,如圖4所示。
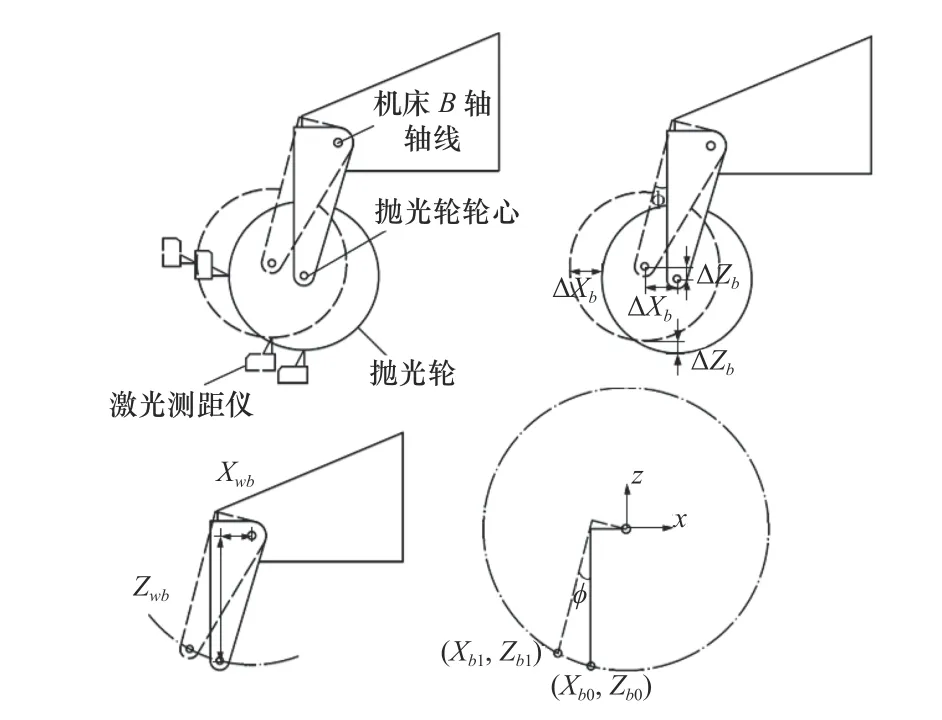
圖4 標定測量計算原理示意圖
以B軸軸線在XOZ面投影為坐標原點,X與Z軸正方向建立坐標系,可得到待測結構參數與測量點位信息的幾何關系,多次計算求取均值,以減小測量誤差帶來的影響,提高標定精度,如式(5)~(7)。
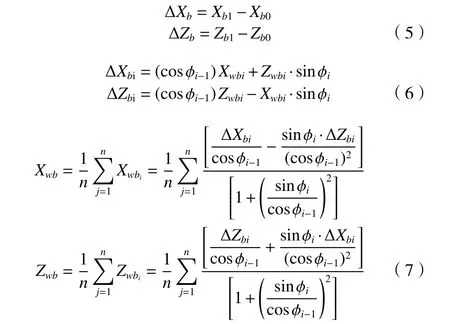
2 標定實驗
2.1 A軸軸線與拋光輪標定實驗
標定用的標準方形件為尺寸200 mm×200 mm×200 mm,精度等級0級的鑄鐵方箱,工作面垂直度與平行度為4.5 μm,將其放在機床工作臺上,調整方箱位姿,使其與機床坐標系方向平行。轉動A軸,分別用不同角度下的測頭測量方箱在Y、Z方向的坐標,測頭測量精度為1 μm,得到如表1所示坐標參數。
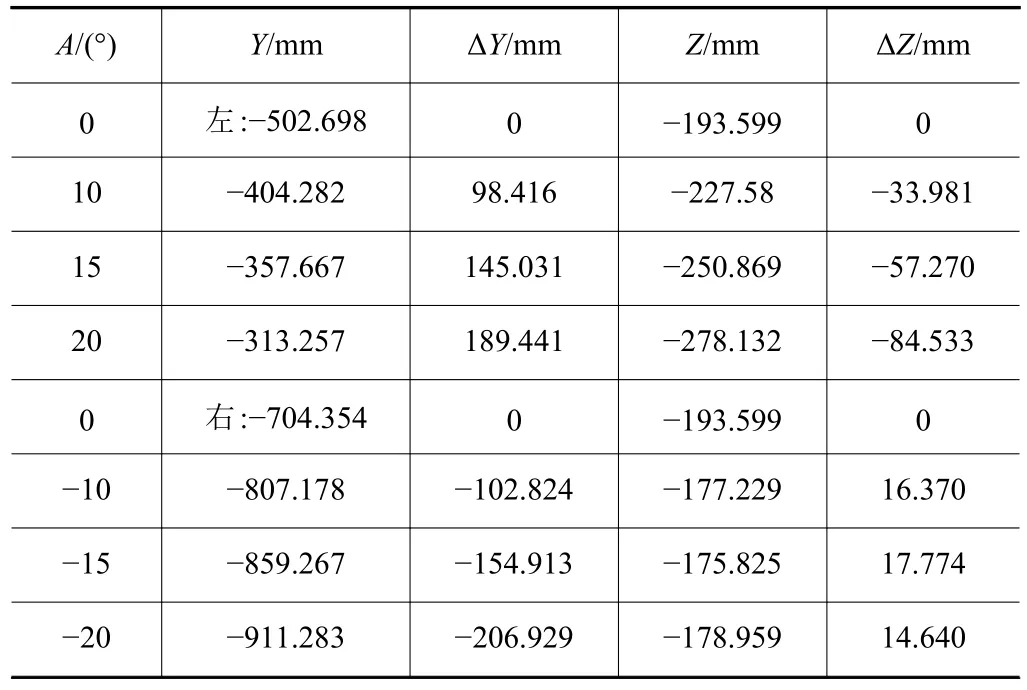
表1 不同A軸角度下測頭坐標值以及對應偏移量
根據式(2),可求解出A軸軸線與測頭的相對位置關系,如表2。

表2 不同A軸角度下結構參數計算值
根據式(2)可求得測頭與A軸軸線的平均相對位置關系,Yma為?144.979 mm,Zma為?579.450 mm。
通過粗略標定獲取拋光點與測頭的大致Y方向距離Ywm0=145 mm。
通過對工件進行平行斑采斑實驗,并計算平行斑中心坐標與工件中心的Y方向偏移量ΔYwm=?0.531 mm,由式(3)可得到拋光點相對于測頭在Y方向上的實際距離,Ywm為145.531 mm。直接測量拋光點與測頭的Z向距離Zwm為180.017 mm。
根據式(4)可得到拋光點相對機床A軸軸線的實際相對位置關系,即Ywa為0.552 mm,Zwa為?399.433 mm。
2.2 B軸軸線與拋光輪標定實驗
經過A軸與測頭,測頭與拋光點標定后,可以尋找到拋光點在拋光輪軸線方向(Y方向)的位置,將激光位移傳感器移動至該位置,再通過調整激光位移傳感器與拋光輪的相對位置尋找拋光輪X、Z方向最低點。
實驗采用了米銥ILD2200-40的激光位移傳感器,其分辨率達到0.6 μm,量程40 mm,最大回光夾角±30°,滿足本次測量需求,測量系統如圖5所示。測量過程如圖6所示,將此時將傳感器置零,經激光位移傳感器測量,拋光輪在該軸向位置存在27 μm的圓度輪廓誤差,需要旋轉拋光輪,并將傳感器移動至平均值為0的位置,如圖7,記下此時機床坐標值。
圖5 激光位移傳感器測量系統

圖6 激光位移傳感器測量拋光輪X、Z方向最低點
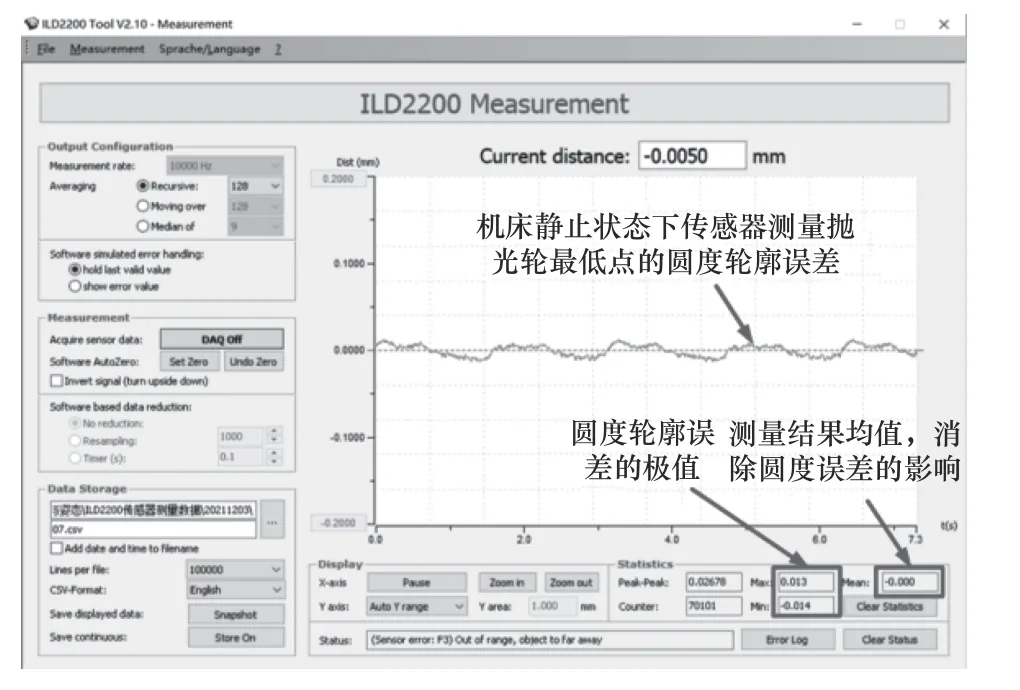
圖7 激光位移傳感器測量界面
轉動B軸,分別測量不同角度下的拋光輪X、Z方向最低點位置坐標,得到如下表3所述坐標參數。
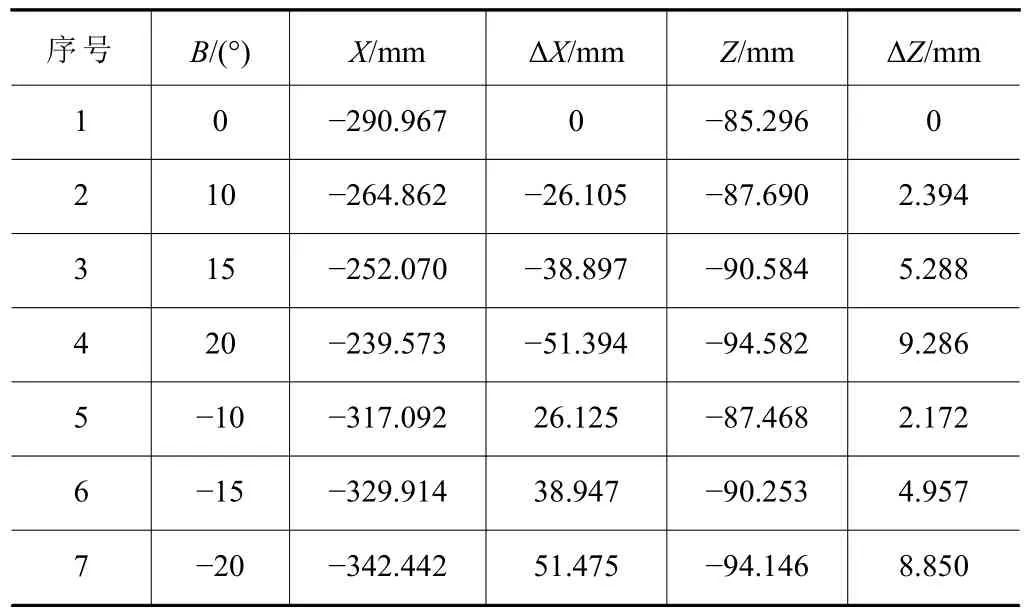
表3 不同B軸角度下拋光輪最低點坐標值以及對應偏移量
根據式(7),可求解出B軸軸線與拋光輪圓心的相對位置關系,如表4。
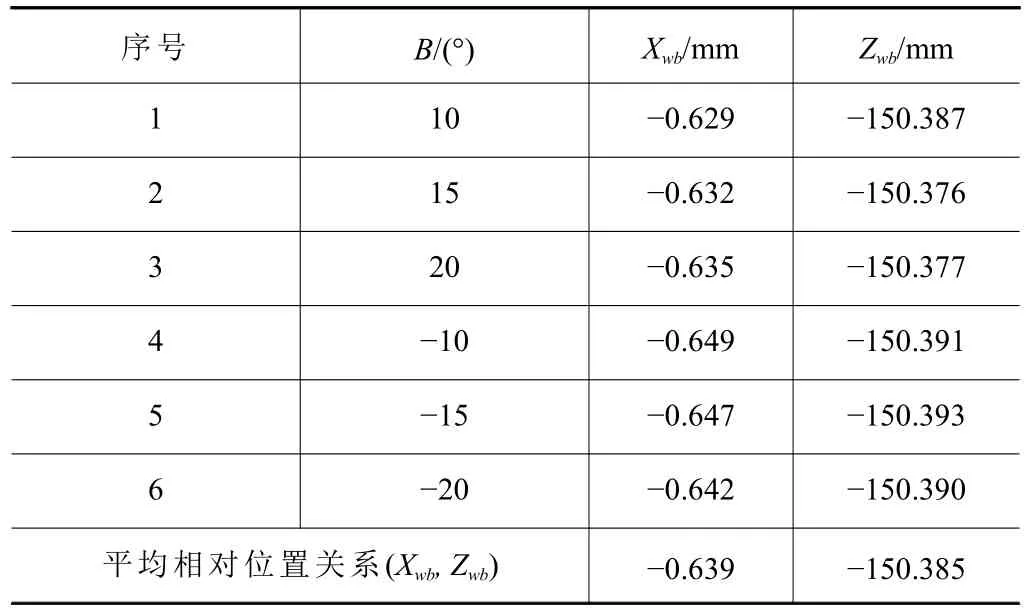
表4 不同B軸角度下結構參數計算值
經千分表多次標定得到B軸軸線與拋光輪圓心距離為X方向?0.642 mm,Z方向?150.378 mm,與千分表測量結果相比,X方向誤差ΔXwb為0.003 mm,Z方向誤差ΔZwb為0.007 mm,皆小于0.01 mm。
3 標定結果準確性驗證與分析
3.1 A軸軸線與測頭參數標定驗證
為了驗證A軸軸線與測頭結構參數的準確性,將機床A軸隨機旋轉一定角度,并根據標定得到的結構參數與A軸旋轉角度,預測測頭分別接觸方形件時Y、Z方向的坐標。
A軸結構參數的標定誤差主要來自機床定位誤差ω1,測頭測量誤差ω2以及用于標定的工件垂直度與平面度的誤差ω3。由于測頭精度為1 μm,測頭測量工件的落點為工件邊角附近的3 mm內的位置,平面度與垂直度對測量影響極小,影響標定精度的主要誤差為定位誤差ω1。由于A軸的兩個結構參數數值較大,對應的定位誤差對標定參數的影響也較大,又因為該誤差為隨機誤差,因此可以通過多次標定來提高測量精度。開展驗證實驗,觀察測量值與預測值偏差是否在誤差允許范圍內,實驗結果如表5~6所示。
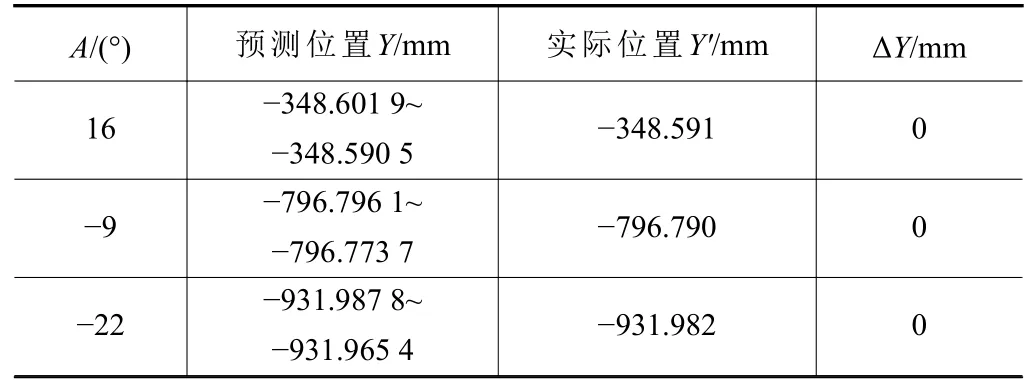
表5 不同A軸角度下測頭Y向坐標預測與實際值
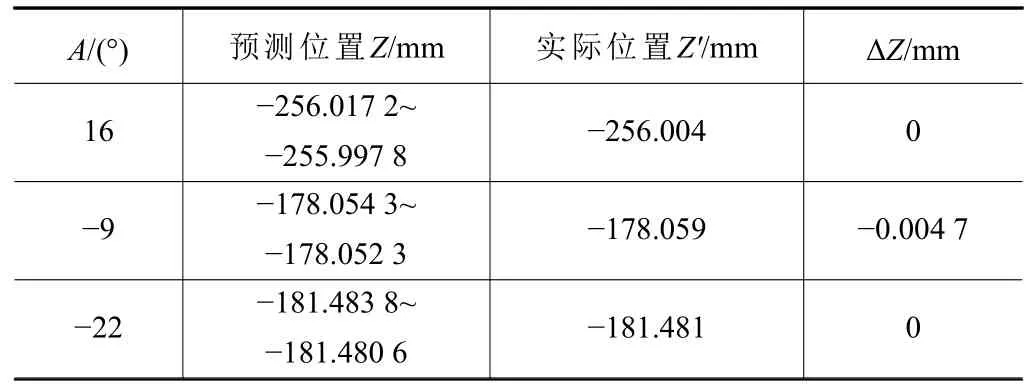
表6 不同A軸角度下測頭Z向坐標預測與實際值
3.2 B軸軸線與拋光輪參數標定驗證
為驗證激光位移傳感器標定方法的準確性,將機床B軸隨機旋轉一定角度,并根據標定得到的結構參數與B軸旋轉角度,預測拋光輪在此時X、Z方向最低點的坐標。
B軸結構參數的標定誤差主要來自機床定位誤差ω1,激光位移傳感器測量誤差ω2以及拋光輪圓度輪廓誤差ω3。激光位移傳感器分辨率小于1 μm,拋光輪的圓度輪廓誤差為25 μm,但在旋轉狀態中測量取測量均值可將該誤差消去,因此標定精度的主要誤差為定位誤差ω1。由于B軸的兩個結構參數相差了2個數量級,定位誤差對較小的參數影響較大,又因為該誤差為隨機誤差,因此可以通過多次標定來提高測量精度。
使用激光位移傳感器對其測量驗證,觀察測量值與預測值偏差是否在誤差允許范圍內,實驗結果如表7~8與圖8所示。
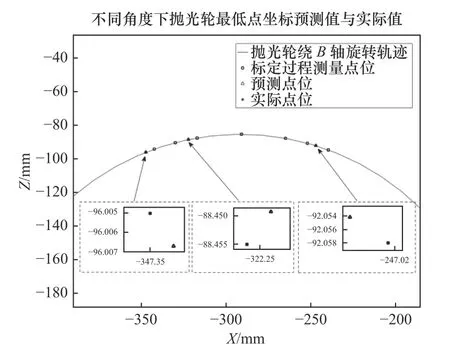
圖8 不同B軸角度下拋光輪坐標預測值與實際值對比示意圖
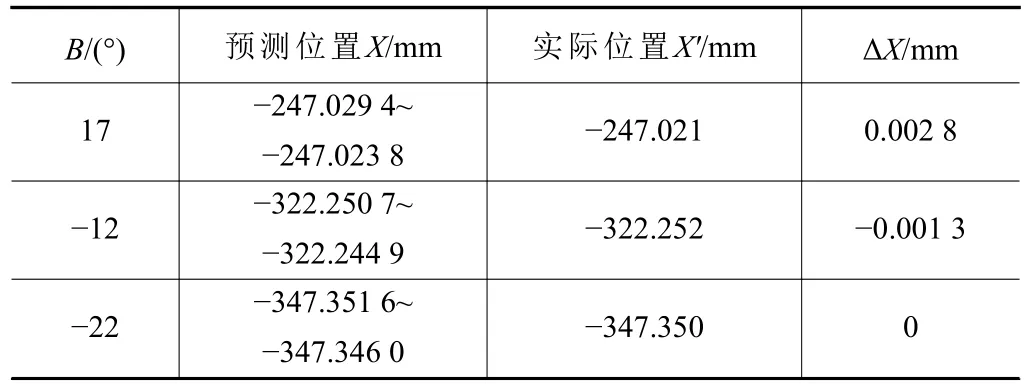
表7 不同B軸角度下拋光輪X方向最低點坐標預測值與實際值
由測量結果可知,使用測量標定出的結構參數,預測出的測頭坐標預測值與實際值偏差以及拋光輪最低點的位置坐標與實際測量出的結果偏差均小于0.006 mm,標定參數準確性與可重復性較高。
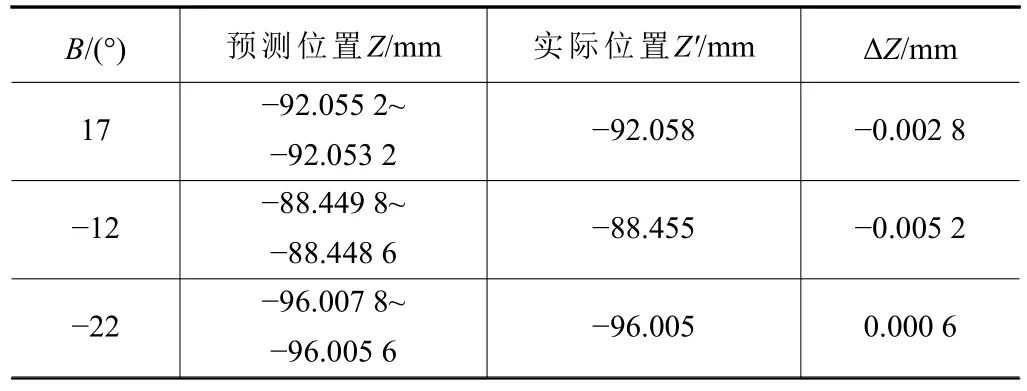
表8 不同B軸角度下拋光輪Z方向最低點坐標預測值與實際值
4 結語
本文實現了一種應用于五軸磁流變機床AB軸結構參數的標定方法。通過分析機床結構特點,對目標標定參數進行分解,利用在機測頭與激光位移傳感器分別建立了A軸與測頭、測頭與拋光點和B軸與拋光點標定方法及模型。通過多次標定可以有效提高標定精度,并根據標定方法所測出的結構參數,分別預測了測頭與拋光輪在不同AB軸角度下的位置,預測值與實際值得偏差皆小于0.006 mm,滿足實驗要求,證明了該方法的可行性。

