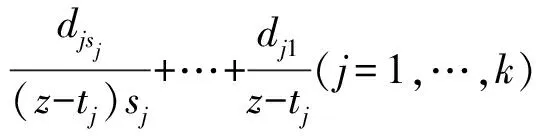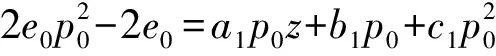差分Painlevé方程組解的存在性和增長級

邱 迪，蔣業陽

(江西科技師范大學數學系，江西 南昌 330038)

1 引言與主要結果

在本文中，我們假定讀者熟悉Nevanlinna理論的基本概念、符號和復差分方程領域的一些基礎知識，詳細內容參見[1,2]。在文獻[3]中我們了解到Painlevé方程與許多數學和物理問題密切相關，并且許多解析的、幾何的和代數的性質不斷被發現，1893年，E.Picard提出下列方程是否具有Painlevé性質的代數微分方程的重要問題。

ω″=f(z,ω,ω′)

(1.1)

Painlevé P.和他的合作者們解決了這一問題，他們指出若方程(1.1)具有Painlevé性質，則可劃歸為五十類典型的方程，但僅有六類方程產生新的超越函數，這六類方程就是著名的Painlevé Ⅰ-Ⅵ方程。眾所周知離散的Painlevé Ⅲ方程在所有的離散Painlevé方程中占有特殊的地位，這是第一個在某些物理應用中被發現能產生超越函數的方程。發現不久之后，文獻[4-5]就證明了該方程具有可積性，這為我們研究Painlevé Ⅲ方程奠定了良好的基礎。

1991年，Ramani A.等[6]首先引進了Painlevé Ⅲ方程的離散形式：

(1.2)

隨后Grammaticos B.等[7]對方程(1.2)進行一系列的變量代換，得到了兩種不同的連續極限形式

(1.3)

和

(1.4)

顯然，連續的Painlevé Ⅲ方程有兩種不同的規范形式，我們可通過方程的有效參數的個數來區分。眾所周知，離散的Painlevé Ⅲ方程是其連續極限對應的完美模擬。正如文獻[8]所示，下列方程

(1.5)

正是方程(1.3)和(1.4)的自然離散模擬。更有趣的是文獻[8]還介紹了方程(1.5)可重寫成一組方程組

其中θ和κ是常數,κ和η關于n是線性的。這是一個深刻的結果，因為方程組中的每一個方程都有離散Painlevé Ⅱ方程的形式。

由于連續變量和離散變量的本質不同，復差分方程解的性質的研究成為時下復分析的熱點之一。例如，在2000年，Ablowitz、Halburd和Herbst等[9]根據離散方程的可積性把離散方程看作是復平面上的時滯方程，他們認為所有的離散差分方程都有明顯的分析方法，因此可使用復分析的方法來研究，特別是Nevanlinna的值分布論的方法。正是因為這種方法的滲透和應用，差分和差分方程從實數域發展到復數域成為了必然結果。在復數域上的擴展可幫助我們獲得更本質的認識，許多數學工作者如Halburd,Korhonen以及Ronkainen等人[10-14]做了許多關于差分Painlevé方程的解的研究，特別地，Ronkainen在2010年研究了差分Painlevé Ⅲ方程的亞純解得出了下述定理：

定理A[12]假設方程

ω(z+1)ω(z-1)=R(z,ω)

(1.6)

有一個超級小于1的可允許的亞純解ω，其中R(z,ω)是關于ω的不可約的有理函數，關于z的亞純函數，那么ω要么滿足一個差分Riccati方程

其中α(z),β(z),γ(z)是代數體函數，要么方程(1.6)可轉化為下列方程之一：

ω(z+1)ω(z-1)=

(1.7)

(1.8)

(1.9)

ω(z+1)ω(z-1)=h(z)ω(z)m

(1.10)

在(1.7)式中，系數滿足κ(z)λ(z+2)λ(z-1)=κ(z-1)λ(z)λ(z+1)，λ(z+1)μ(z)=κ(z),λ(z-1)μ(z+1)，κ2(z)μ(z+1)μ(z-1)=μ2(z),和下列情況之一：

(1)η≡1,ν(z+1)ν(z-1)=1,κ(z)=ν(z)；

(2)η(z+1)=η(z-1)=ν(z),κ(z)≡1。

在(1.8)式中，系數滿足η(z)η(z+1)和λ(z+2)λ(z-1)=λ(z)λ(z+1)。

在(1.9)式中，系數滿足下列情況之一：

(1)η(z)≡1并且要么λ(z)=λ(z+1)λ(z-1)要么λ(z+3)λ(z-3)=λ(z+2)λ(z-2)；

(2)λ(z+1)λ(z-1)=λ(z+2)λ(z-2),η(z+1)λ(z+1)=λ(z+2)η(z-1),η(z-1)η(z)=η(z+2)η(z-3)；

(3)η(z+2)η(z-2)=η(z)η(z-1),λ(z)=η(z-1)；

(4)η(z)λ(z)=η(z+2)η(z-2),λ(z+3)λ(z-3)=λ(z+2)λ(z-2)λ(z)。

在(1.10)式中，h(z)是代數體函數并且m∈Z,|m|≤2。

在此之后，自然就會更進一步想到復差分Painlevé方程組的解的存在性上去，更關鍵的是我們注意到離散Painlevé Ⅲ方程的自然離散模擬可化為含PainlevéⅡ方程的方程組，因此結合定理A我們考慮更一般的差分Painlevé方程組的解的情況。我們主要考慮下列方程組

(1.11)

其中α(z),β(z),γ(z),a(z),b(z),c(z)都是關于z的多項式。

但在這篇文章中我們僅研究了方程組(1.11)的一種特殊情況α(z)=a(z)=0,β(z),b(z)是關于z的線性函數，γ(z),c(z)是常數，因此我們的方程可寫為

(1.12)

其中a1,a2,b1,b2,c1,c2都是常數且a1,a2不等于0。

定理1.1設a1,a2均為非零常數，則差分方程組(1.12)不存在有理函數解。

例1在方程(1.12)中，設a1=a2=0，b1=-1，b2=c1=c2=1則方程組

定理1.2若c1≠±2且c2≠±2,設(x(z),y(z))是差分方程組(1.12)的一組有限級超越亞純解，則我們有ρ(x)=ρ(y)≥1。

注記1在定理2的證明中我們發現若(x(z),y(z))是方程組(1.11)的一組解并且系數α(z),β(z),γ(z),a(z),b(z),c(z)分別是x(z),y(z)的小函數，那么也一定有ρ(x)=ρ(y)。

2 引理

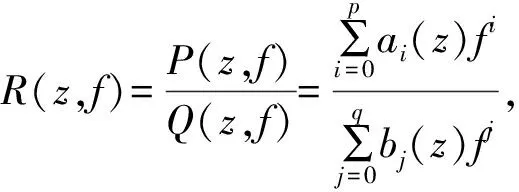
那么我們有T(r,R(z))=max{p,q}T(r,f)+S(r,f)。

引理2.2[17]設f(z)是一個ρ=ρ(f),ρ<∞的亞純函數,并且設η是一個固定的非零復數，那么對于?ε>0，我們有：

T(r,f(z+η))=T(r,f)+O(rρ-1+ε)+O(logr)

引理2.3[2]設g在平面上是一個級小于1的超越亞純函數。設h>0,則存在一個ε集合Ε使得當z在C/Ε內趨于∞時，滿足|c|

那么g在|ξ-z|≤h內沒有極點或零點。

3 定理的證明

(3.1)

其中e0,e1,…,em是常數。

同理，我們可把y(z)表示為

(3.2)

其中p0,p1,…,pn是常數。

對于(3.1)式,我們可斷定e1=…=em=0。如若不然，我們可假設em≠0(m≥1)，則當z充分大時，有

x(z)=emzm(1+o(1)),x(z+1)=em(z+1)m(1+o(1))=em(1+o(1))

(3.3)

對于(3.2)式，我們也斷定p1=…=pn=0，如若不然我們可假設pn≠0(n≥1),當z充分大時，則有

y(z)=pnzn(1+o(1)),y(z-1)=pn(z-1)n(1+o(1))=pn(1+o(1))

(3.4)

將(3.3)式和(3.4)式代入差分方程組(1.12)得到：

(3.5)

和

(3.6)

由于m≥1,因此(3.5)式左右兩邊的次數不相等，故出現矛盾。

由于n≥1,因此(3.6)式左右兩邊的次數不相等，也出現矛盾。

因此，e1=…em=p1=…pn=0。

接下來，我們證明e0=0,p0=0,如若不然，e0≠0,p0≠0,則當z充分大時，我們有

(3.7)

同理有

(3.8)

(3.9)

不妨設

s(z)=szk+sk-1zk-1+…+s0

(3.10)

h(z)=hzt+ht-1zt-1+…+h0

(3.11)

m(z)=mzl+ml-1zl-1+…+m0

(3.12)

n(z)=nzu+nu-1zu-1+…+n0

(3.13)

其中s,sk-1,…,s0,h,ht-1,…,h0,m,ml-1,…,m0,n,nu-1,…,n0均為常數且shmn≠0顯然有k

h(z)s(z+1)m(z)2+h(z+1)s(z)m(z)2-n(z)2h(z)s(z+1)-s(z)n(z)2h(z+1)=a1zn(z)h(z)h(z+1)m(z)+b1n(z)h(z)h(z+1)m(z)+c1m(z)2h(z)h(z+1)

(3.14)

和

m(z)n(z-1)s(z)2+n(z)m(z-1)s(z)2-m(z)n(z-1)h(z)2-n(z)m(z-1)h(z)2=a2zn(z-1)s(z)h(z)+b2n(z)n(z-1)s(z)h(z)+c2n(z)n(z-1)s(z)2

(3.15)

根據(3.14)式左右兩邊的次數關系我們有：l-u+1=k-t。但根據(3.15)式左右兩邊的次數關系我們又有：k-t+1=l-u這顯然是不可能的。因此差分方程組(1.12)不存在有理函數解。

定理1.2的證明我們先證ρ(x(z))=ρ(y(z)).由差分方程組(1.12)我們有：

(3.16)

(3.17)

對于(3.16)式和(3.17)式右邊的式子運用引理2.1得：

(3.18)

(3.19)

根據特征函數的運算性質，我們得到：

T(r,x(z+1)+x(z))≤T(r,x(z+1))+

T(r,x(z))

(3.20)

T(r,y(z)+y(z-1))≤T(r,y(z-1))+

T(r,y(z))

(3.21)

根據引理2.2有：

T(r,x(z+1))+T(r,x(z))=2T(r,x(z))+O(rρ-1+ε)+O(logr)

(3.22)

T(r,y(z))+T(r,y(z-1))=2T(r,y(z))+O(rρ-1+ε)+O(logr)

(3.23)

由(3.16)，(3.18)，(3.20)和(3.22)有

2T(r,y(z))+S(r,y(z))≤2T(r,x(z))+

O(rρ-1+ε)+O(logr)

(3.24)

由(3.17)，(3.19)，(3.21)和(3.23)有

2T(r,x(z))+S(r,x(z))≤2T(r,y(z))+

O(rρ-1+ε)

(3.25)

由增長級定義，以及式子(3.24)和(3.25)可得ρ(x(z))=ρ(y(z))。不失一般性，我們令ρ(x(z))=ρ(y(z))=ρ，現要證ρ≥1，我們不妨假設ρ<1,則通過引理2.3可知存在一個ε-集合E，使得在CE中z→∞.那么我們有

x(z+1)=x(z)(1+o(1))

(3.26)

y(z-1)=y(z)(1+o(1))

(3.27)

將(3.26)和(3.27)代入差分方程組(1.12)得

經計算得：

(3.28)

和

(3.29)

在(3.28)式中，我們令

P(z,y(z))=[2(c12-4)y(z)5+4c1(a1z+b1)y(z)4+2((a1z+b1)2+8)y(z)3-8y(z)](1+o(1))Q(z,y(z))=[2c2(a2z+b2)+c2c12]y(z)4+[2(a1z+b1)(a2z+b2)+2c1c2(a1z+b1)]y(z)3+[c2(a1z+b1)2-2c1(a2z+b2)]y(z)2-2(a1z+b1)(a2z+b2)y(z)

那么我們有P(z,y(z))=Q(z,y(z))，但由于c1≠±2且y(z),x(z)都是超越的。顯然有

T(r,P(z,y(z)))=5T(r,y(z))+S(r,y(z))

T(r,Q(z,y(z)))=4T(R,y(z))+S(r,y(z))

這是一個矛盾。同理，對于(3.29)式也有同樣的矛盾。因此ρ≥1。