基于GWO-SVM的石化旋轉機械軸承故障診斷1

莫常春，劉美，費繼友，張清華，張斐，吳斌鑫，3，周正南，3

(1.廣東石油化工學院 自動化學院，廣東 茂名 525000；2.大連交通大學 機車車輛工程學院，遼寧 大連 116028；3.吉林化工學院 信息與控制工程學院，吉林 132022；4.東莞理工學院 機械工程學院,廣東 東莞 523419 )

故障診斷是確保石化機組“安、穩、長、滿、優”運行非常重要的步驟[1]。石化現場事故的統計數據顯示，因軸承故障而引發的事故占比很大，因此有必要對旋轉機械軸承進行故障診斷。在故障診斷領域，特征參數法比較常用，波形指標、峰值指標、裕度指標、脈沖指標、峭度指標等一系列時域無量綱指標由于具有不受現場工況影響的特性，在故障特征提取中得到廣泛應用[2]。但無量綱指標在某些故障數據間存在重疊，對某些故障特征不是很敏感。熊建斌等[3]提出了互無量綱指標的數據處理方法，解決了傳統無量綱指標存在的不足，并有效應用于石化機組故障診斷。覃愛淞等[4]通過遺傳編程構建出了具有最佳分類能力的新無量綱指標，并將其應用到石化機組的故障診斷中，在軸承故障診斷中取得了相當好的效果。Chapelle等[5]在提出了一種機器學習算法——支持向量機(SVM)，目前SVM在故障診斷領域得到了廣泛運用，故障診斷分類效果較好。但是影響SVM模型分類性能的懲罰因子C和核函數參數γ相關文獻并沒有給出確切的方法。基于此，本文提出了一種基于互無量綱指標和灰狼算法優化的SVM模型的石化旋轉機械軸承故障診斷方法[6]。本文采用灰狼算法(GWO)對SVM進行參數優化，可避免算法出現局部最優、收斂性差、搜索效率低等問題，有效地應用于石化機組11kW5級離心風機滾動軸承的故障診斷。

1 互無量綱指標

傳統無量綱指標之間存在嚴重的數據重疊，再加上現有的無量綱指標只對滾動軸承的部分故障特性敏感，導致故障辨識分類效果并不理想。互無量綱指標在傳統無量綱的基礎上進行改進，采用一種新的無量綱數據融合計算方法，構造出新的故障特征證據體——互無量綱指標，互無量綱指標克服了傳統的無量綱指標數據重疊的問題，且對故障特征更加敏感，同時互無量綱指標不受載荷和轉速的變化影響，因此互無量綱指標在故障診斷領域得到很好的應用[7]。

(1)

式中：р(s)和р(y)分別為s和y的概率密度函數。

式(1)取不同系數，構建出5個不同的互無量綱指標，分別為

(2)

(3)

(4)

(5)

德國前總理格哈德·施羅德說，習近平主席是一位遠見卓識的改革家。他把馬克思主義原理與中國實際結合，緊隨時代進行創新，提出了雄心勃勃的改革計劃，涵蓋了各個領域。實踐證明行之有效，深得人心，是實現中國夢的基本方略，也是開辟人類更加美好未來的行動指南。巴西中國問題研究所所長羅尼·林斯認為，中國共產黨不僅能獨立自主有效地治理自己的國家，而且將以更加積極的姿態參與全球治理。

(6)

2 灰狼算法優化支持向量機

2.1 支持向量機

支持向量機因其能夠有效且可靠地解決分類問題，在旋轉機械故障診斷中得到廣泛應用[8]。最主要的算法思想是通過核函數將低維線性不可分樣本映射到高維空間，尋找一個超平面對樣本進行分割，分割的原則是實現間隔最大化，從而達到分類目的[9]。

設有n個線性可分的樣本(x1,y1),(x2,y2),…,(xn,yn)，x∈Rμ，y∈{+1,-1}， ，其中μ代表數據的維度，y=+1和y=-1分別表示樣本數據的兩個類別，分類超平面如式(7)表示：

WTx+b=0

(7)

對于尋求分類超平面，通過引入拉格朗日乘數法理論，再轉變成對偶問題進行求解，如式(8)所示。

(8)

(9)

其中本文支持向量機算法采用的核函數為RBF核函數為

(10)

由此可見，影響SVM模型分類精度的兩個參數主要是懲罰因子C和核函數參數γ[10]。目前，這兩個參數的選取還沒有相關文獻給出具體的解決辦法。因此，本文引入灰狼算法對支持向量機的兩個重要參數進行優化，從而構建出辨識分類精度以及運行效率更高的GWO-SVM石化旋轉機械滾動軸承故障診斷模型。

2.2 灰狼算法(GWO)

GWO算法是模擬自然界中灰狼群體的社會等級機制和捕獵行為而衍生出來的一種新型群體智能優化算法，GWO算法能夠實現目標參數優化，具有較好的收斂性等特點[11]。算法中狼群有α、β、δ、ω四個等級，如圖1所示。

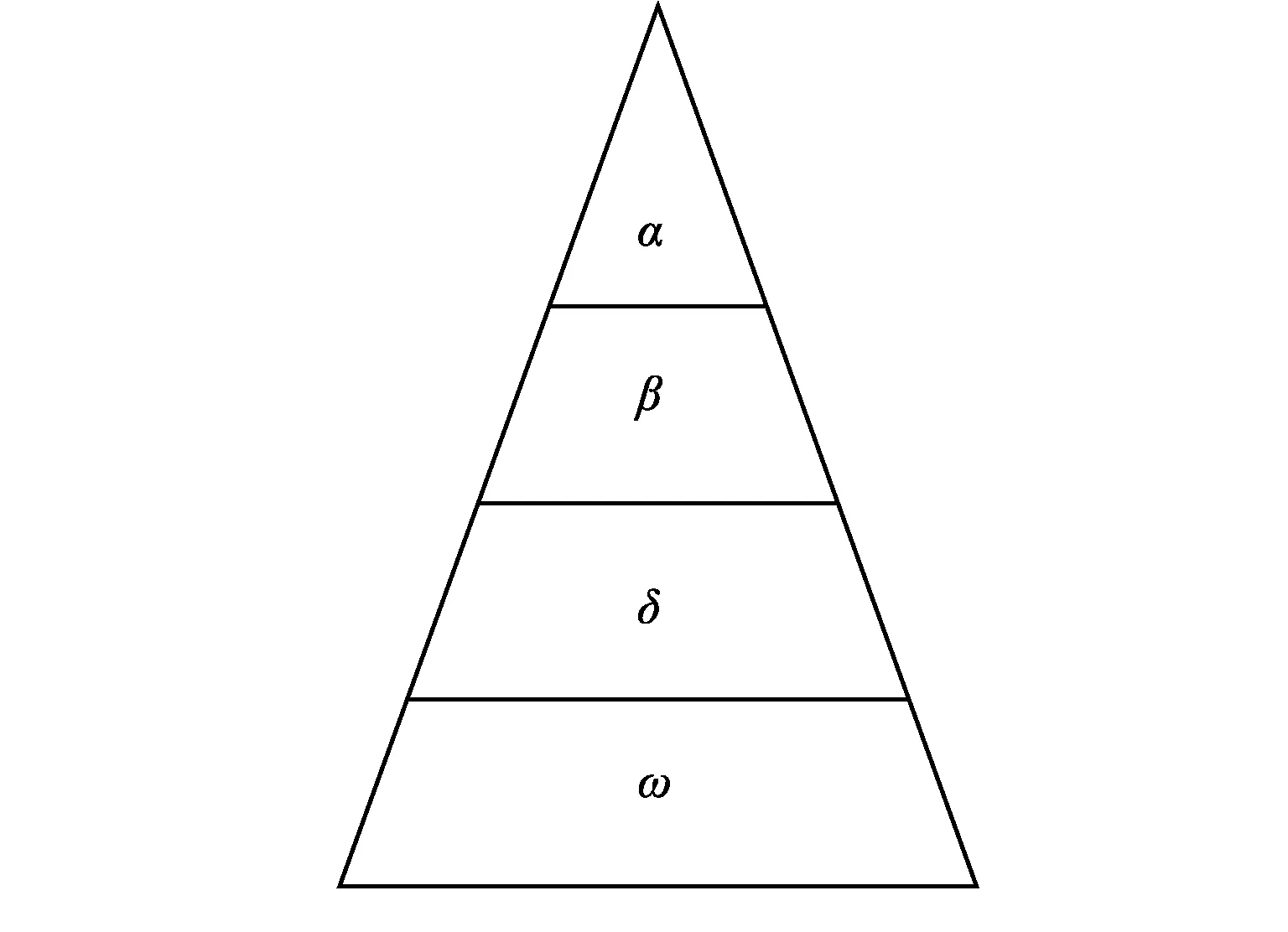
圖1 灰狼等級層次制度

GWO算法中，α(頭狼)為待求問題最優解，β(二級狼)和δ(三級狼)分別記為次優解和次次優解，其余解(剩下的狼)均設為ω。狼群中把α、β、δ三頭狼作為初始值帶領狼群在空間尋找獵物(最優解)或者不斷逼近(不斷迭代)。

捕捉獵物 (參數尋優)時，狼群對獵物進行包圍，不斷逼近獵物，尋找全局最優解，且不斷更新位置，位置表示如下：

X(t+1)=Xp(t)-W·[B·Xp(t)-X(t)]

(11)

式中：X(t)為灰狼目前所在位置；Xp為獵物位置；B為擺動因子，

B=2r2；W為收斂因子，W=2ar1-a；a為迭代控制系數，a=2-2t/Nmax；r1和r2為[0，1]之間的隨機數；t為灰狼算法當前的迭代次數；Nmax為最大迭代次數。

GWO算法中，狼群中α、β、δ起到引導的作用，自動更新個體位置。

X1=Xα-A1·[B1·Xα(t)-X(t)]

(12)

X2=Xβ-A2·[B2·Xβ(t)-X(t)]

(13)

X3=Xδ-A3·[B3·Xδ(t)-X(t)]

(14)

Xp(t+1)=(X1+X2+X3)/3

(15)

式中：Xα為最優解(頭狼α)的位置；Xβ和Xδ分別為次優解(二級狼β)和次次優解(三級狼δ)的位置；A1、A2、A3和B1、B2、B3為隨機數產生的不同系數；X1、X2、X3為狼群中領導層更新后的位置。

灰狼捕獵成功，獲得最優解，灰狼狩獵行為主要以式(11)中值所體現，迭代次數從2線性減小至0完成，當W≤1時，灰狼集體出動攻擊獵物，相當于算法局部搜索；當W>1時，灰狼算法進行全局搜索。

2.3 實驗背景與數據來源

為了驗證GWO-SVM故障診斷模型的可行性，通過對廣東省石化裝備故障診斷重點實驗室石化多級離心風機故障診斷平臺軸承采集的實驗數據進行驗證。多級離心風機故障診斷平臺由變頻電機、負載控制器、變速箱、多級離心風機、EMT390振動數據采集器以及各種故障件組成，其中滾動軸承實驗故障件如圖2所示。

圖2 石化旋轉機械滾動軸承故障件

實驗主要以軸承常見的4種不同故障 (軸承缺滾珠、軸承內圈磨損、軸承外圈磨損、正常軸承)開展研究，數據采集與處理的具體過程如下。

(1)使用EMT390數據采集器在多級離心風機垂直部位采集4種類型的機殼振動加速度數據，每種故障采集2次，每次50組數據。其中，每一組數據有1024個機殼振動加速度，4種故障類型的原始振動波形如圖3所示。

圖3 正常軸承以及軸承不同故障類型信號時域

(2)使用數據采集器的數據管理系統將采集到的數據保存為mat文件。

(3)用MATLAB對所采集的各種故障數據進行處理，構造互無量綱指標，再將5個互無量綱指標構成的數據集矩陣進行編號。

(4)從采集的滾動軸承原始數據中隨機抽取50組數據，組成一個含有200組故障數據的訓練集，通過matlab中的ramdom函數隨機選取50%的數據集作為模型訓練集，另外50%作為測試集。滾動軸承4種狀態下的時域圖如圖3所示。

本文提出一種基于互無量綱指標和GWO-SVM的故障診斷方法，故障診斷具體流程如下：(1)把樣本數據集分為兩部分，一部分為訓練集，另一部分為測試集。(2)選取訓練集數據作為SVM的輸入，然后用灰狼算法對支持向量機參數C和γ進行優化，更新適應度，狼群數量設為30，設置最大迭代次數為600，求解C和γ的最優值，得到訓練出具有較高辨識能力的SVM 分類模型。(3)將石化旋轉機械軸承測試集輸入GWO-SVM模型進行故障辨識分類。(4)輸出診斷結果。

3 實驗結果分析

為了驗證GWO-SVM軸承故障診斷模型的可行性和優越性，將SVM模型與遺傳算法優化支持向量機(GA-SVM)模型同本文提出的GWO-SVM模型進行比較。實驗數據選取正常軸承、軸承外圈磨損、軸承內圈磨損以及軸承缺滾珠4種故障類型，并分別隨機抽取數據80組，總共的樣本數為320組。通過MATLAB中的random函數隨機選取數據選取50%(160組)作為故障診斷模型的訓練集，剩下的50%(160組)作為故障診斷模型的測試集，傳統支持向量機(SVM)、遺傳算法優化支持向量機(GA-SVM)、灰狼算法優化支持向量機(GWO-SVM)這3種算法辨識分類結果如圖4～6所示，這3種算法故障診斷結果性能指如表1所示。

圖4 SVM模型故障診斷結果 圖5 GA-SVM模型故障診斷結果 圖6 GWO-SVM模型故障診斷結果

由表1可知，在對正常軸承、軸承外圈磨損、軸承內圈磨損以及軸承缺滾珠4種故障類型數據進行實驗時，從算法的軸承故障辨識分類準確度來看，GWO-SVM模型的軸承故障辨識分類的準確率明顯高于SVM和GA-SVM這兩種算法。在算法運算時間上來看，GWO-SVM算法運算效率明顯高于SVM和GA-SVM這兩種算法，算法運行時間大大縮短。由此可知，本文提出的灰狼算法優化的支持向量機在性能方面比支持向量機以及遺傳算法優化支持向量機的故障診斷效果優越，能有效地運用于大型石化旋轉機械滾動軸承的故障診斷。

表1 三種算法故障診斷結果性能指標SVMGA-SVMGWO-SVMC0.8367.6949.367γ4.5796.7648.927時間/s72.32611.6327.231準確率/%76.2586.2590.00

4 結語

針對廣東省石化裝備故障診斷重點實驗室石化多級離心風機故障振動信號非線性和非平穩性的特征以及支持向量機分類算法參數選擇困難的問題，本文提出了一種利用灰狼算法優化支持向量機參數的方法，利用灰狼算法獨有的全局優化能力對支持向量機兩個重要參數進行選擇優化。結果表明，本文所提出的算法在大型石化旋轉機械軸承故障診斷中準確率高、運行時間短，為石化大機組滾動軸承故障診斷提供了一種切實可行的方法。