銅合金編織網網片阻力水槽試驗研究

王 磊,王魯民,萬 榮，劉永利,齊廣瑞，宋 煒

(1中國水產科學研究院東海水產研究所，農業農村部東海與遠洋漁業資源開發利用重點實驗室,上海200090；2上海海洋大學海洋科學學院,上海 201306)

銅合金材料在海水環境中具有耐海水腐蝕，抗海洋污損生物附著等特性[1-2]。相比傳統纖維網衣，銅合金網衣的特點使其在海水養殖網箱及養殖圍欄上的應用發展迅速，其中銅合金編織網在大型柱樁式圍欄上的應用具有一定代表性[3-4]。銅合金編織網是將銅合金線進行雙向隔波彎曲，先軋后編而成的方孔平紋編織網，其互鎖結構使網片結構較為穩定[5]。通過連接柱樁，銅合金編織網構成的圍攔網可以經受較強浪流作用，且抗生物附著特性可以保持水體流通，降低魚類病害發生率[6]。隨著養殖設施裝備的發展及深遠海養殖的發展需求，大型養殖圍欄作為一種可面向外海的養殖設施，其結構設計與安全性評估需要有更可靠的科學數據支撐，其中網衣的受力及強度設計是重要一環。常見的漁用網衣多為柔性網衣，眾多學者通過水槽試驗和數值模擬進行網衣的受力研究[7-14]。國內外學者也已開展過銅合金網衣的水動力性能等研究相關研究[15-19]，雖然銅合金網衣相比合成纖維網衣具備剛性的特點，但其研究方法和水動力衡量參數是基于柔性網衣的研究基礎，也是通過水槽試驗或數值模擬等研究方法，研究關注的內容主要是獲得不同種類的銅合金網衣在水中的受力，及其與合成纖維網衣的受力性能對比等。

本研究通過開展銅合金編織網的水槽試驗，獲得可適用于養殖設施的多個規格銅合金編織網網片的水阻力數據，并結合數值曲線回歸獲得常用規格的銅合金編織網阻力值計算公式，同時基于試驗數據初步分析獲得網片的阻力系數與雷諾數的關系，為深遠海大型圍欄養殖設施的網衣受力計算及網衣水動力性能分析提供參考。

1 材料和方法

1.1 銅合金編織網

試驗網片為銅合金編織網，選用系列規格直徑和網目尺寸的銅合金線制成。網目為方形網目，網片及網目尺寸見圖1。截取試驗用網片尺寸均為500 mm×500 mm。

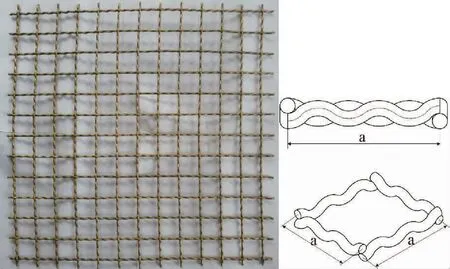
圖1 銅合金編織網網片及網目尺寸Fig.1 The mesh size of copper alloy woven net

選用的銅合金線直徑為2.5 mm、3.0 mm、3.5 mm、4.0 mm、4.5 mm和5.0 mm，由于金屬制網機難以精準控制網目尺寸，以測量得到的網目尺寸為準，見表1，網片編號對應“線徑-網目尺寸”。

表1 試驗網片種類及規格表Tab.1 Main particulars of the net used in the test

1.2 試驗概況

試驗地點為中國水產科學研究院東海水產研究所靜水池，水池主尺度：90 m(長)×6 m(寬)×3 m(深)。拖車速度精度：相對精度P≤1%。

試驗網片安裝于可旋轉框架上，其旋轉角度定位精度為0.01°。

本試驗測力數據采集使用LSM-B-500NSA1-P型三分力傳感器(量程500N)，試驗模型安裝示意圖見圖2。

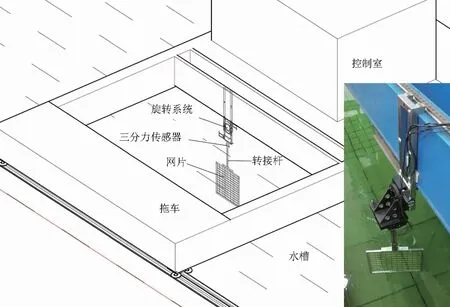
圖2 網片水槽試驗安裝示意圖Fig.2 A sketch of experimental setup of nets in water tank

1.3 試驗方法

1.3.1 試驗數據測試方法

試驗網片安裝于不銹鋼方形框架上，分別在流速v=0.30 m/s、0.45 m/s、0.60 m/s、0.75 m/s、0.85 m/s (水溫15℃) 開展試驗，其中沖角在0°～90°區間，每間隔10°為一個測錄數據點，數據為阻力Fx和升力Fy。

圖3 網片水動力性能試驗參數定義示意圖Fig.3 Definition of parameters related to net test in water tank

1.3.2 試驗網片阻力與升力計算方法

在試驗過程中，網片所在平面與水流(拖車前進)方向平行時定義沖角α為0°，三分力傳感器隨網片轉動而同時轉動，因此網片(帶框架)的阻力為三分力傳感器在水平面上的讀數(Fx與Fy)沿流速方向的合力。

阻力：

Fnx=(Fx-Fkx)cosα+(Fy-Fky)sinα

(1)

升力：

Fny=(Fx-Fkx)sinα+(Fy-Fky)cosα

(2)

式中：Fx為網片與框架于三分力傳感器X向的受力讀數；Fy為網片與框架于三分力傳感器Y向的受力讀數；Fnx為網片阻力；Fny為網片升力；Fkx為框架于三分力傳感器X向的受力讀數；Fky為框架于三分力傳感器Y向的受力讀數；α為網片沖角，即網片所在平面與水流方向的夾角。

所有試驗數據都進行了框架干擾修正，框架干擾修正是采用對應扣除框架(無網衣)的受力(Fkx和Fky)方法來完成。

1.3.3 銅合金網衣的阻力計算方法

漁用網具、網箱網衣及養殖圍欄網衣等都是由網片拼接組成，拼接網片的材料和規格也不一定相同，而網衣的規格通常包含了網目尺寸、網線直徑及網衣的編織型式。公式(3)是目前通用的平面網片阻力計算公式[20]：

R=ρSv2Cx/2

(3)

式中：R為阻力，N；ρ為水的密度，1 000 kg/m3；Cx為阻力系數，無量綱常數；S為特征面積，m2，v為流速，m/s。

由公式(3)，可得阻力系數Cx的計算公式：

Cx=2R/(Sρv2)

(4)

由于銅合金編織網與常見的合成纖維網特性不同，可以將銅合金編織網作為剛性體進行計算(水流作用下無形變)，銅線的直徑可直接采用游標卡尺等測量。特征面積S即線面積，是構成網片的銅合金線投影面積，如規定網目總數Nm的矩形銅合金編織網，其構成網片的線面積Sk為：

Sk=Nm4ad

(5)

式中：a為網目尺寸(目腳長度)，m；d為網線直徑，m。

18F-FDG PET/CT測量食管鱗癌病變長度及預測T、N及G分期的臨床價值(王 菲)(5):429

為研究銅合金編織網各流速狀態下雷諾數與阻力系數的關系，銅合金編織網的網平面與流速方向垂直時，可將網線作為圓柱體進行水動力分析，則雷諾數計算的特征長度為網線直徑。

Re=ρdv/μ

(6)

式中：Re為雷諾數，無量綱常數；μ為水的動力黏滯系數，0.001 14 Pa·s。

2 結果與分析

2.1 結果

試驗獲得的數據經采用公式(1)和公式(2)處理后得到銅合金編織網網片的阻力Fnx和Fny，如表2的數據是編號4.0-40的網片在不同流速、不同流速沖角下的水阻力數據。

表2 銅合金編織網4.0-40網片阻力數據(N)Tab.2 Resistance data of net with a size 4.0-40 mm(N)

將試驗獲得各編號網片阻力數據進行歸納整理，并利用公式(3)～(5)進行計算，可以獲得對應規格銅合金編織網的阻力系數，網片在與流速方向垂直(90°)時，銅合金編織網的線面積可采用公式(5)獲得，表3數據是不同線徑規格網片(網目尺寸50 mm)在90°沖角及對應流速下的阻力系數。

表3 銅合金編織網網片阻力系數CxTab.3 Drag coefficient of copper alloy woven net

2.2 分析

2.2.1 網片阻力與迎流沖角的關系

圖4中Fnx-α曲線是由編號 4.0-40規格網片的阻力數據(表2)繪制的對應流速下網片阻力值與迎流沖角α的變化關系。由圖可見，隨著迎流沖角的增大，網片的阻力值也在增加，網片的迎流面積變化是造成網片阻力值變化的因素之一，網片的緯向(橫向)銅線隨著網片的轉動(α角度變化)，使緯向的銅線迎流面積發生變化，同時由于銅合金編織網的銅線是波浪形結構(圖1)，也造成了經向(豎向)銅線的迎流面積發生變化，故而網片阻力值也產生變化。

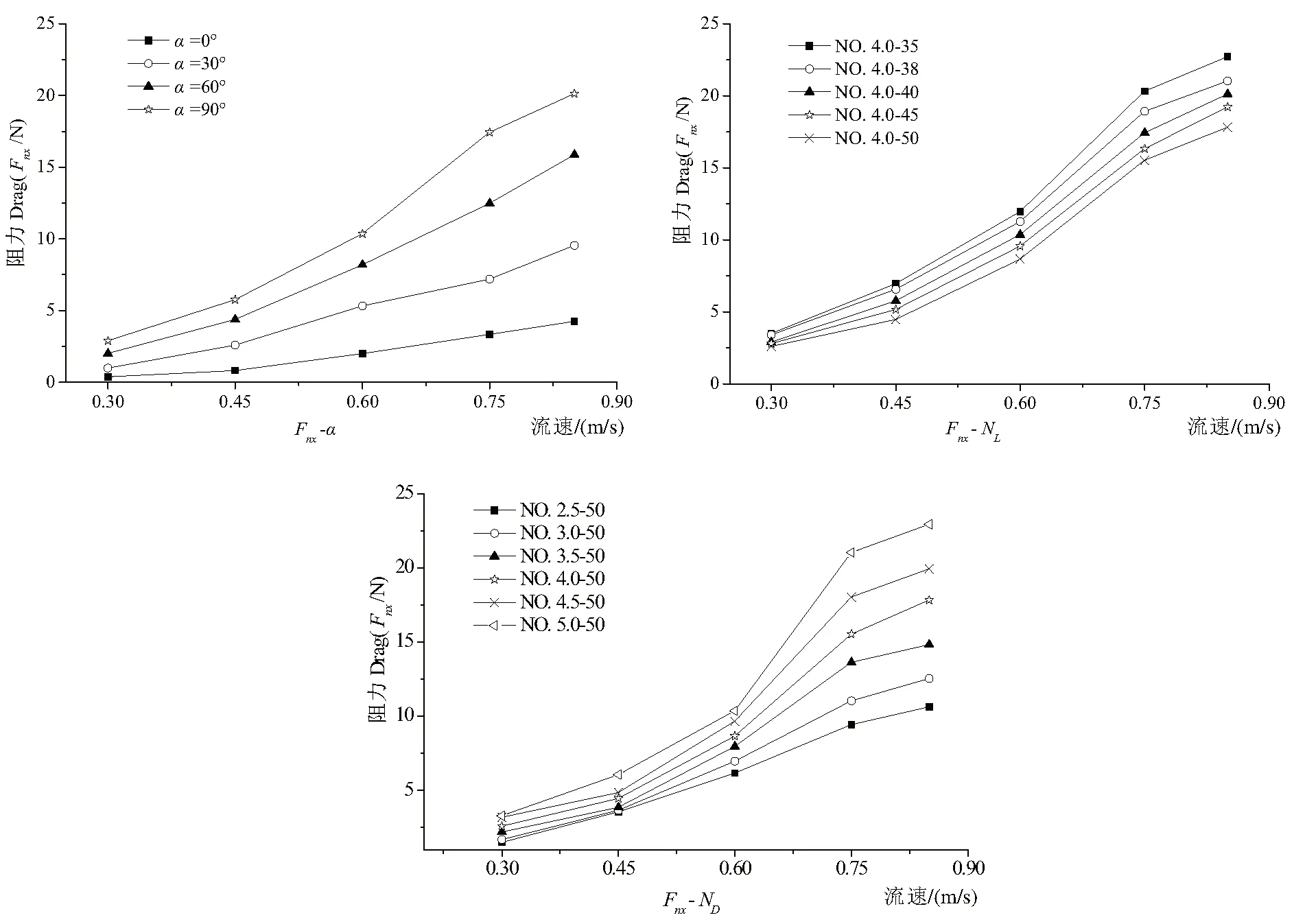
圖4 網片阻力在不同流速下與網目尺寸、沖角、線徑的關系Fig.4 The changing curve grouping comparison of net drag in several velocity along with the mesh size,angle of attack and wire diameter

圖4中Fnx-NL曲線圖是線徑4.0對應5個規格網目尺寸的網片在水流沖角α=90°時的阻力數值隨流速變化的曲線。由圖4可見，不同規格網目尺寸的網片產生的Fnx-NL曲線趨勢基本一致，阻力值隨流速的增加而增大，同時由圖中也可以看出在各對應流速下，阻力值與網目尺寸的變化關系，隨著網目尺寸的增大，阻力值是降低的，這是因為網目尺寸增加使單位面積網片的網線數量減少，即網線的迎流面積減小，使阻力值降低。

2.2.3 網片阻力與銅線線徑的關系

圖4中Fnx-ND曲線圖是選取網目測得的網片阻力值曲線。由圖4可見，隨著銅線線徑的增加，網片的阻力值是增加的，網目尺寸不變，表示每個規格銅線線徑網片的銅線長度相同，由于線徑的變化造成網片迎流面積的變化，這是網片阻力值變化的主要原因。

2.2.4 網片阻力系數與雷諾數的關系

雷諾數Re是研究網片水動力性質的一個重要參數，是流速及特征長度的函數，由公式(6)可知，銅線線徑是網片雷諾數的特征長度，將雷諾數Re及網片的阻力系數Cx進行分析，兩者的變化關系是網片水動力性能研究的重要指標[21]。通過公式(6)計算6種線徑銅合金編織網在網片平面垂直流速方向、網片平面平行流速方向，不同流速下的雷諾數，并結合表3本試驗數據繪制雷諾數Re與阻力系數Cx的點狀圖，見圖5。

圖5 網片阻力系數與雷諾數的關系Fig.5 The relationship between the drag coefficient and the Reynolds number of the mesh

基于點狀圖采用冪函數回歸，得到雷諾數Re與阻力系數Cx的關系公式(7)和(8)。

Cx90=1.690 5Re-0.032

(7)

Cx0=0.003 4Re0.5638

(8)

公式(7)和(8)中：雷諾數Re范圍為658～3 727；Cx90為網片平面垂直于流速方向的阻力系數，范圍為1.12～1.65；Cx0為網片平面平行于流速方向的阻力系數，范圍為0.08～0.34。

3 討論

3.1 不同規格網衣的阻力

單位面積的網片，增大網目尺寸和降低網線直徑，都會使線面積減小，水阻力降低。

陳昌平等[19]通過水槽試驗和數值模擬的方法，對3種規格目腳長度和3種規格網線直徑的金屬網片進行了網衣受力研究，研究也表明隨著網線直徑的增大，網衣受力增加，隨著目腳尺寸的增大，網衣受到的水阻力值減小，其變化趨勢與本研究一致。

基于本試驗系列規格銅合金編織網的試驗數據，利用多項式回歸可以得到不同規格網片隨流速的變化曲線，公式(9)～(18)是本試驗10種規格網片(線徑-網目尺寸)在沖角90°時單位面積(1 m2)網片隨流速變化的受力公式：

網片規格2.5-50：F=62.896v1.916 7

(R2=0.987)

(9)

網片規格3.0-50：F=73.684v1.982 4

(R2=0.988)

10)

網片規格3.5-50：F=85.400v1.952 5

(R2=0.977)

(11)

網片規格4.0-50：F=97.940v1.943 7

(R2=0.985)

(12)

網片規格4.5-50：F=107.900v1.883 1

(R2=0.974)

(13)

網片規格5.0-50：F=127.176v1.952 7

(R2=0.969)

(14)

網片規格4.0-35：F=127.576v1.857 3

(R2=0.987)

(15)

網片規格4.0-38：F=117.168v1.814 1

(R2=0.986)

(16)

網片規格4.0-40：F=112.828v1.918 8

(R2=0.992)

(17)

網片規格4.0-45：F=105.304v1.916 0

(R2=0.992)

(18)

式中：F為水流沖角90°時網片單位面積的水阻力，N/m2；v為水流速度，m/s；R2為擬合優度。該系列公式可為本試驗涉及規格銅合金編織網在不同流速下的水阻力計算提供計算依據。

3.2 網片阻力與沖角

漁具型式及養殖設施網體形狀決定了網衣在使用時是與水流成多角度的，因此網衣與水流沖角的關系是網衣水動力研究的重要內容[22-25]。漁網與網箱使用的網衣多為柔性纖維網衣，因此關于平面網片的阻力研究多以柔性網衣為對象，如詹杰民等[26]基于流體力學試驗，研究了流向對平面合成纖維網衣受力的影響，認為當網片與流向垂直時阻力值最大，隨著網片平面與流向的角度逐漸減小其阻力值降低。

銅合金編織網在水流作用下，因其金屬特性不易產生拉伸變形，故其阻力研究方法自適應于已有的網片水動力研究理論。圖6是銅合金編織網4.0-40在各試驗流速下，網片阻力和阻力系數與沖角的關系，可見，該關系變化趨勢與詹杰民等[22]利用柔性纖維網衣的流體力學試驗結論相一致。

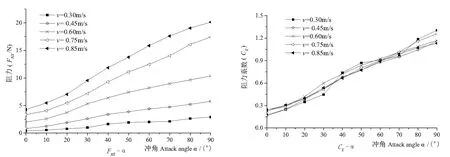
圖6 網片阻力及阻力系數與沖角的關系Fig.6 The relationship between the net drag and drag coefficient and the angle of attack

現有的研究表明，當網衣平面與水流角度發生變化后，網片的水阻力變化是與網線在垂直流向平面的投影面積有直接關系[27]，由公式(5)，即其特征面積S是在垂直流速平面上構成網線的銅合金線投影面積Sk，該面積值與流速沖角有關系，沖角越小，Sk越小，因此網衣的水阻力也越小。陳天華等[28]采用計算機模擬方法研究了樁柱式圍網單元柔性網衣的受力，研究表明網線的最大張力值隨沖角的增大而增大，其變化趨勢與網片投影面積隨角度的變化相似。

參照列維恩平面網片阻力理論假說[20]，網片平面與流速成一定角度時的阻力和阻力系數的計算公式為：

Rα=RD0+(RN90-RD0)sinα

(19)

Cα=CD0+(CN90-CD0)sinα

(20)

在公式(19)和(20)中，RD0、RN90分別為網片與流速垂直和平行時的阻力；CD0、CN90分別為網片與流速垂直和平行時的阻力；Rα、Cα分別為網片與流速成α角度時的阻力和阻力系數；α為網片平面與流速夾角。

圖6中網片的阻力系數隨沖角的變化趨勢基本一致，與田內、今井健彥、克魯和列維恩等[20]提出的在各種角度下的研究結論相一致。基于公式(20)及圖6中的Cx—α曲線，經數據擬合，銅合金編織網4.0-40在不同沖角下的阻力系數計算公式中，CD0為0.21，CN90為1.20，與田內公式接近(CD0=0.27，CN90=1.1)。

3.3 銅合金編織網水動力性能

銅合金編織網由于其結構特性，在流體中的水動力性能即具有單柱體流體特性，又具有網形狀的流態疊加影響特性，尤其波紋狀的網線結構，使網衣在不同沖角下的微觀受力分析更為復雜。由本試驗數據得出的阻力計算公式(8)～(17)看出，在阻力與速度冪函數的關系中，速度的冪值范圍均小于2，這表示流態沒有處于自動模型區，尚處于低雷諾數的流態轉換區[20]，對于銅合金編織網養殖設施的模型試驗研究，需要參考網衣受力的模型試驗準則[29]。

銅合金編織網的結構與材料特性，也直接影響了其水動力性能，Tsukrov 等[17]采用水槽試驗方法對銅合金編織網、尼龍網、銅合金斜方網等數種網衣進行水動力性能分析比較，結論認為銅合金編織網的阻力系數(網衣平面垂直流速)相比合成纖維網衣較低，但相比銅合金斜方網等金屬網的阻力系數較高；這是因為銅合金斜方網的網線沒有銅合金編織網的波紋銅線結構，結構較為簡單。

銅合金編織網的水動力計算，通常是基于平面網片的水動力分析理論，通過大量的試驗數據建立網片阻力計算經驗公式，如國外學者弗里特曼、田內等[20]，國內學者虞聰達等[30]都是基于大量水槽試驗，結合理論分析提出網片水阻力計算的經驗公式。本研究基于試驗數據，推導得出以公式(7)和(8)為代表結論的銅合金編織網的網衣阻力系數與雷諾數的對應關系，該公式結合公式(20)可用于推導處于本試驗雷諾數范圍內的網衣阻力系數。

4 結論

網片的阻力在固定水流沖角下是隨著流速的增加而增大，同時在特定流速下，網片的阻力隨著水流沖角的增加而增大(沖角90°為網片平面與水流垂直)，并根據數據曲線回歸得到在沖角90°時單位面積系列規格銅合金編織網隨流速變化的水阻力計算公式；通過網片阻力與網片規格及沖角變化的分析，認為網片阻力與網片的特征面積有直接關系，即特定流速下，銅合金編織網的銅線在與水流垂直平面的線面積投影越大，則其阻力值越高；基于試驗數據分析了銅合金編織網阻力和阻力系數隨沖角的變化情況，雷諾數與阻力系數的關系等，并結合相關經驗公式給出了銅合金編織網阻力系數的計算公式。本研究結果可以為銅合金編織網的水阻力計算及水動力性能分析提供參考。

□