基于有限元與深度學習的BLT圖像重建方法

張暄軒，曹 旭，張久樓，張 琳

(1.西安郵電大學 通信與信息工程學院，陜西 西安 710121;2.西安電子科技大學 生命科學技術學院，陜西 西安 710071；3.南京醫科大學 醫學影像學院，江蘇 南京 210029；4.山東師范大學 信息科學與工程學院，山東 濟南 250014)

生物發光斷層成像(Bioluminescence Tomography,BLT)是一種預臨床成像技術，其通過采集生物體表透射出的生物發光，能夠非侵入式地揭示活體動物體內的功能活動[1-2]。生物發光位于可見光或近紅外波段，產生自生物體內的某些生物發光反應，如熒光素酶催化反應。生物發光的機理來源于分子層面的化學反應，因此生物發光光源的分布能夠反映這些特異性分子的分布，成為一種重要的分子影像技術。作為一種分子影像技術，BLT通過編碼生物發光蛋白基因，能夠可視化地體現多種多樣的細胞層面和亞細胞層面的生物過程，業已在諸多生物醫學研究中展現出強大的潛力，如腫瘤放療[3]、癌細胞檢測[4]和治療評價[5]。

BLT的成像理念類似于諸如擴散光學斷層成像[6](Diffuse Optical Tomography,DOT)和熒光分子斷層成像[7](Fluorescence Molecular Tomography,FMT)的其他光學斷層成像技術，都是通過探測生物體表的光子密度，再利用數學模型反向推算出以某種物理參數為對比度的斷層圖像。不同的是，BLT的光源位于生物體內并且不需要外部激發。考慮不需要外部激發光源，BLT的測量數據不會像FMT那樣被背景光干擾，使得BLT具有更高的靈敏度。在BLT的成像過程中，需要先在生物體表測量生物發光的光子密度，再建立某種數學模型描述生物發光在生物體內的擴散過程。最后，利用測量數據求解該數學模型的逆向問題重建出生物發光光源的分布。擴散方程[8]是最常用的正向模型，其是輻射傳輸方程的一種近似，方程形式為一個橢圓型偏微分方程，能夠被許多數值方法求解，如有限元方法[8](Finite Element Method,FEM)。基于正向模型，能夠通過最小化測量數據與正向模型的預測值之間的差距建立逆向問題。類似于其他光學斷層成像技術，BLT的逆向問題也具有高度病態性，其由測量數據的維度與待重建參數的維度之間的不平衡造成[9]。在BLT中，生物體表所獲取的測量數據具有部分相關性，且不能像DOT和FMT中那樣通過增加投影角度擴增，使得BLT的病態性問題要比DOT和FMT更加嚴重。為了增加BLT測量數據的多樣性，通常需要采集多個波長下的生物發光圖像[10]。此外，如果直接使用DOT或FMT中的算法，如采用牛頓型算法[8]進行BLT圖像重建，逆向問題的病態性會惡化圖像重建結果的質量。為了獲取可靠的重建結果，BLT重建通常需要添加額外的信息，如利用來自其他成像模態的解剖結構信息正則迭代過程[11-13]，或是利用可行域縮小待重建參數的維度[14-16]。但是，這些方法并不總是可用的，解剖結構信息需要額外的成像模態[9]，而可行域的選擇需要一定的先驗信息[15]。

近年來，深度學習[17](Deep Learning，DL)受到了各個領域的廣泛關注，特別是圖像領域，而近些年關于深度學習在醫學成像中應用的報道主要集中在圖像處理或分析[18]。嘗試利用深度學習構建圖像重建方法的研究則集中出現于近兩三年，其結果顯示，基于深度學習的圖像重建方法具有巨大潛力[19]。這些研究涵蓋了廣泛的成像模態，包括X射線計算機斷層成像[20-22](X-ray Computed Tomography,X-CT)、磁共振成像[23-24](Magnetic Resonance Imaging,MRI)、正電子發射斷層成像[25](Positron Emission Tomography,PET)以及多種光學斷層成像技術，如DOT[26]、FMT[27]和BLT[28]。深度學習是一種數據驅動型機器學習方法，能夠通過學習從數據中抽取出兩個相關數據域之間的映射關系。利用機器學習策略實現圖像重建時，深度學習既可以被用在圖像域也可以被用在數據域。對于圖像域，神經網絡可以被用來獲取兩種不同條件下圖像的轉換關系，如被噪聲污染的圖像與無噪聲圖像之間的轉換關系。嚴格來說，這種策略是一種后處理方法而不是圖像重建，但通常卻被用來解決某些傳統圖像重建問題，如X-CT中的低劑量重建[20]、稀疏角度重建[21]、有限角度重建問題[22]以及MRI中的稀疏重建[23]。對于數據域，深度學習可以被用來預處理數據或是構建一個端到端的模型直接將原始數據轉換為斷層圖像，如Würfl等[22]提出了一種含有錐形束反投影層的深度學習方法實現端到端的X-CT有限角度重建；Zhu等[24]針對MRI提出了一種由若干卷積層和全連接層組成的端到端神經網絡，稱為流形逼近自動變換(Automated Transform by Manifold Approximation,AUTOMAP)，實現數據域到圖像域的直接重建； Yedder等[26]嘗試使用端到端的卷積神經網絡實現從DOT投影數據到斷層圖像的直接重建；Guo等[27]提出一種三維深度編碼-解碼網絡實現端到端的FMT圖像重建；Yao等[28]使用一種4層的端到端全連接神經網絡實現BLT圖像重建。

在以往的研究中，BLT的圖像重建策略被迭代法所主導。迭代法計算耗時，且需要一個較精確的數學模型描述生物發光的傳輸過程。與迭代法相比，DL作為一種數據驅動型機器學習方法，一旦神經網絡被訓練好，即具有極快的推斷速度，且能夠直接從數據中抽取映射關系，不需要人為選擇特殊的正向模型。DL的應用難點在于收集大量數據用以訓練神經網絡。文獻[28]的研究顯示了通過深度學習實現BLT圖像重建的可行性，其所使用的數據集由蒙特卡洛方法[29]生成。蒙特卡洛方法通過大量重復單個光子在生物體內的傳輸過程并統計結果實現對光場分布的估計，其精度由所重復的光子個數所決定，通常需要重復上億個光子。雖然大量的光子能夠保證精度，但同時也耗費了較長的計算時間。考慮深度學習需要大量的訓練數據和測試數據，計算時間問題的考量對于深度學習的應用尤為重要。BLT中被成像物體和被成像目標會隨著所研究問題的不同有所變化，需要對不同的研究問題生成不同的數據集，這就增強了對數據生成速度的要求。使用FEM求解擴散方程[8]的策略可以作為另一種數據生成的可行方案，相比蒙特卡洛方法，這種方案具有極快的計算速度。因此，更適合頻繁生成大規模數據集。

1 基于FEM的BLT數據生成

1.1 擴散方程

擴散方程配以FEM是一種被廣泛使用的光子擴散模擬方法。其中擴散方程是一個橢圓型偏微分方程，源自輻射傳輸方程，是其近似形式，穩態擴散方程式[8]為

(1)

式中：D和μa分別表示擴散系數和吸收系數；Φ(r)表示空間位置r處的光子密度，r∈Ω；X(r)表示光源項，在BLT中即待重建的未知參數；Ω表示求解的空間域，在BLT中即生物體內的空間。

1.2 有限元方程

作為一個偏微分方程，擴散方程在無限介質中的解析解有其確定形式，但具有復雜邊界的介質上的解析解形式卻難以獲得，因而通常使用數值方法求解擴散方程。FEM是求解偏微分方程的常用數值方法之一，其需要將空間域Ω離散為一個由若干節點和單元組成的網格，并將方程中的函數使用基函數展開，由基函數所構成的線性空間被稱為有限元空間。通過離散空間域形成的有限元空間具有有限維度，那么在有限元空間上展開的任意函數都可以被一組展開系數表示，由此能將一個偏微分方程轉化為一個線性方程組求解，稱為有限元方程。

為了描述復雜邊界情況，需要引入以下Robin邊界條件[8]，其表達式為

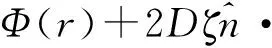
(2)

通過引入Robin邊界條件，能夠通過FEM將擴散方程離散為有限元方程[8]，其表達式為

KΦ=X

(3)

式中：Φ和X分別表示光子密度向量和源向量，都是維度為N的列向量，N表示網格中節點的數量；K是一個N×N的方陣，在FEM中一般被稱為剛度矩陣。矩陣K以及向量X的元素是基函數的函數，表達式分別為[8]

離了林強信，景花廠沒有倒。林強信不甘心，他是個精明的生意人，從不做賠了夫人又折兵的買賣，他不甘心白吃了這個啞巴虧。景花廠后來漸漸有了起色，訂單多了，員工多了，林強信更不甘心了。他要擊敗景花廠，要阿花像只無家可歸的貓，乖乖回到他的懷抱。

(4)

(5)

式中：υ表示有限元空間的基函數；i和j分別表示行或列的索引。

剛度矩陣K是一個稀疏、對稱且滿秩的方陣，因此有限元方程是一個具有唯一解的非其次線性方程組，可以通過諸多成熟的數值方法進行快速求解。對于某一被成像物體，只要先構建相應的幾何體并且進行網格剖分，再構建有限元空間產生剛度矩陣K。同時，通過人為設計構建特定光源分布的X，最后求解有限元方程即可實現大量BLT數據的快速獲取。

2 基于深度學習的BLT圖像重建

2.1 深度學習

深度學習[17]是一種數據驅動型機器學習方法，其能夠使用由多個層級結構結合激活單元所組成的神經網絡近似任意非線性函數。深度學習有兩種標準訓練模式，分別稱為監督學習和無監督學習。在監督學習中，神經網絡需使用成對的輸入數據和標簽數據訓練解決分類或回歸問題，而無監督學習則不需要標簽數據，通常用來尋找數據中的范式。總體來說，無監督學習因其自動挖掘數據范式的能力而更適合人工智能任務，但其研究相對較少，理論體系尚不完善，在許多問題中仍不能使用。與無監督學習相比，監督學習應用的更廣泛，并且只要有標簽數據可用，通常可以獲取可靠的結果。與計算機視覺中的一些問題不同，生物醫學成像對模型的穩定有著較高的要求，如X-CT和MRI圖像常被用來診斷人的疾病，細微的成像圖像差異會造成難以估計的損失。因此，目前大部分有關使用深度學習實現圖像重建的研究均使用監督學習。

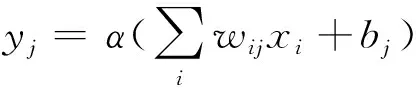
2.2 基于深度學習的光子密度分布補全

為了使真實空域的復雜形狀邊界能夠和離散后的網格邊界更好的貼合，FEM通常使用非結構網格構建有限元空間，二維情形一般使用三角形網格，而三維情形則使用四面體網格。與結構化網格不同，非結構化網格由不規則連接的節點組成，沒有規則的拓撲結構，所有節點的拓撲關系需要進行記憶存儲。而非結構化網格的不規則性會對圖像重建產生影響[7]，其通常會因重建目標的稀疏性增加而加劇。因此，預先測試了直接使用一個全連接網絡構建端到端的BLT圖像重建，結果顯示網格的不規則性會顯著地惡化圖像重建質量。為了消除網格不規則性的影響，利用神經網絡實現光子密度分布的補全而非直接重建出圖像。在生物體表獲取的測量數據實際上是光子密度在表面的采樣值。因此，光子密度分布的補全就是要從體表部分光子密度值推測出整個空間的光子密度分布，在獲取完整的光子密度分布后，再通過將剛度矩陣與光子密度向量相乘獲得生物發光光源分布。光子密度分布是一個連續變化的函數，基本不會受到網格不規則性的影響。受網格拓撲結構的啟發，設計了一種網格拓撲層接入體表測量數據。網格拓撲層由多個子級層級結構組成，子層級之間的連接關系又由網格的拓撲關系決定。所使用的網格拓撲層和神經網絡的組成結構如圖1所示，使用了一個具有少量節點的粗糙三角形網格解析網絡結構。根據拓撲結構，圖1(左)所示的網格的節點可以被分為5層，最外層的節點是表面采樣節點，測量數據是在這些節點上獲取的，根據拓撲連接關系，其余內部節點可以分為4層。網格拓撲層的子層級數量及每個子層級的神經元數量與內部節點的層級結構相對應，相鄰兩個子層級之間的神經元使用全連接。網格拓撲層的輸出是所有子層級輸出的合集，該輸出被接入一個由若干全連接層組成的子網絡，子網絡每層的神經元數為內部節點的總數。最終，子網絡的輸出和輸入的測量數據組成完整的光子密度分布，將其與剛度矩陣相乘得到光源分布。

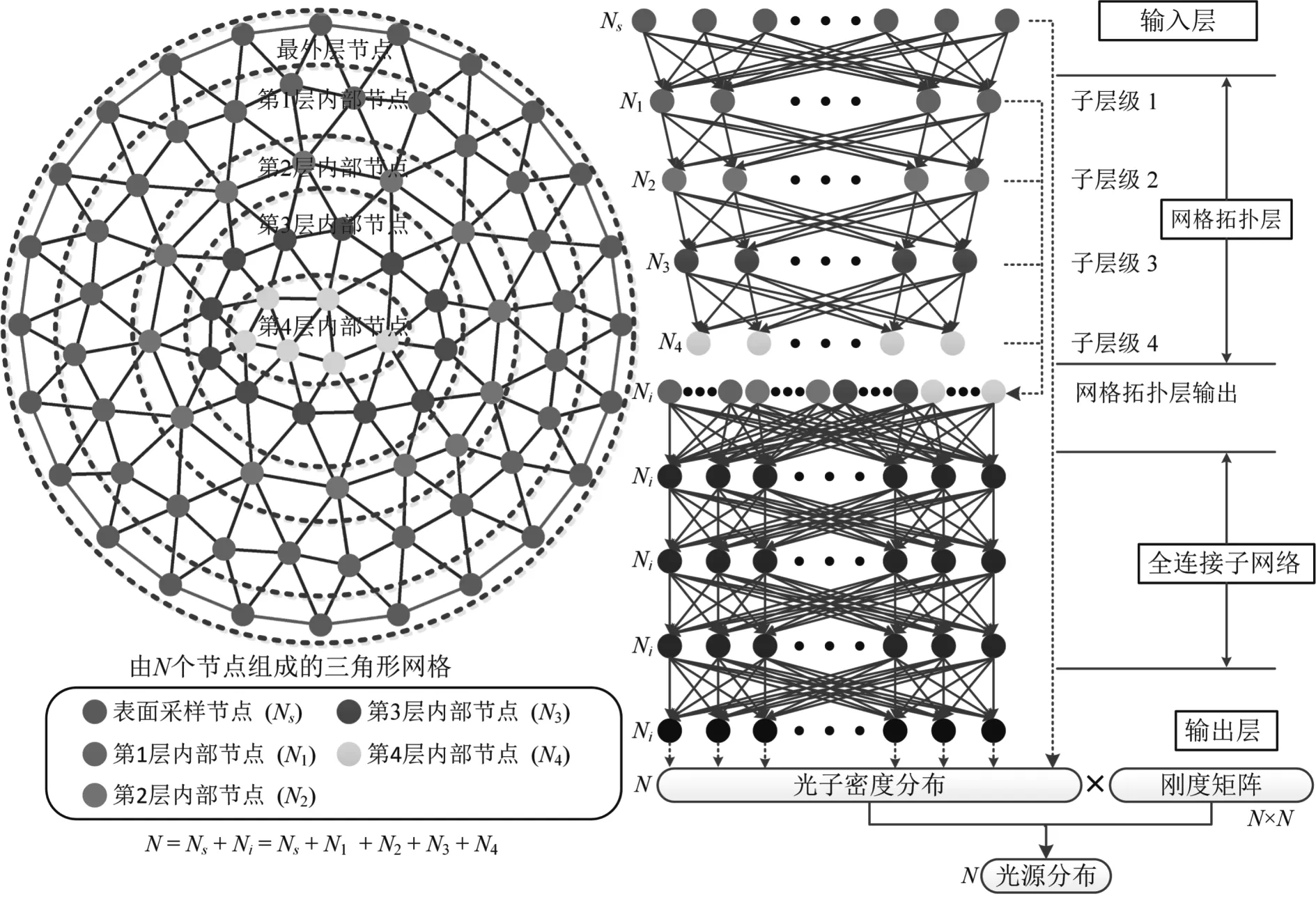
圖1 所使用的網格拓撲層和神經網絡示意圖

3 實驗結果與分析

3.1 實驗設置

為了驗證所提方法，進行了仿真實驗。使用一個直徑為3 cm的圓形物體作為成像介質，其被進一步離散成一個由2 168個節點和4 206個單元組成的三角形網格。通過FEM生成了3個不同數據集分別用于訓練、驗證和測試。訓練集由2 219個樣本組成，每個樣本都是通過在介質中嵌入一個直徑為0.2 cm的圓形光源獲得，光源的位置規則排列在介質內。驗證集和測試集分別由500個樣本組成，這些樣本均使用介質內的隨機光源位置獲得。每個樣本都是由光子密度表面采樣值和內部值所組成的成對數據。神經網絡使用Python 3.6和Tensorflow搭建，訓練的硬件平臺為一臺配有Nvidia GeForce RTX 2080 Ti顯卡和16 GB內存的個人電腦。使用平方損失函數為

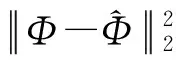
(6)

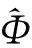
還使用了一個全連接網絡(Fully Connected Network，FCN)[28]和基于可行域的迭代法(Optimized Permission Source Region，OPSR)[14]對測試集數據進行重建。FCN由4個全連接層組成，每層的神經元數與網格的節點數相同。與所提出的方法不同，FCN使用端到端的訓練方式，即網絡的輸入為表面測量數據，而輸出直接為光源的分布。FCN的訓練策略與所提的方法相同。OPSR中的Nf參數設置為1，迭代次數設置為50。

3.2 實驗結果分析

實驗的重建結果如圖2所示，共展示了7組具有代表性的圖像。考慮所提方法使用神經網絡實現光子密度分布的補全，圖2也展示了光子密度的分布，所有圖像均使用最大值進行了歸一化。為了定量評價重建結果，引入了均方根誤差(Root Mean Square Error，RMSE)，其結果如表1所示。進一步對比了處理單幅圖像所需要的計算時間，其結果如表2所示。

圖2 BLT重建結果

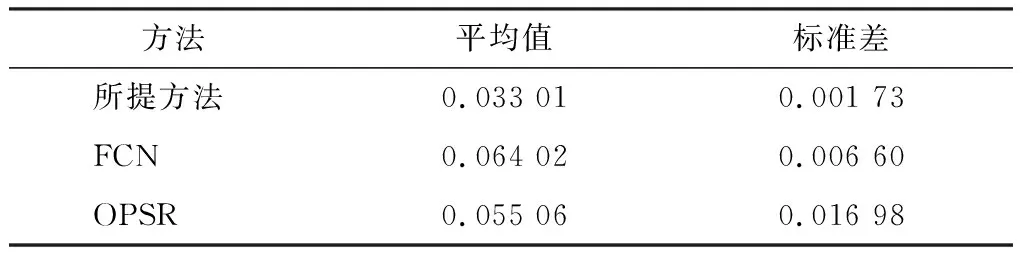
表1 訓練集重建結果的RMSE

表2 單幅圖像的處理時間

由圖2可以看出，所提方法能從表面采樣數據較好地預測介質內整個光子密度分布，即圖2第3行，這種高質量的光子密度補全保證了與K相乘所得的重建結果也具有較高質量，平均RMSE僅為0.033 01，遠小于FCN和OPSR，即圖2第4行和表1第1行。相比之下，FCN的重建結果表現較差，即圖2第5行和表1第2行，重建出的目標趨向于集中在某個或某幾個孤立的點上，這種現象常出現在網格比較細小的光學斷層成像重建中，其主要原因是網格的不規則性。此外，FCN在重建某些目標時會失效，如圖2(e4)，這些樣本的FCN輸出會是一個全為零的空向量。圖2第6行顯示，OPSR能夠重建出目標的位置，但卻很難重建出其輪廓。考慮OPSR是一種迭代法，決定目標輪廓的可行域會在每次迭代時通過移除低貢獻節點的方式進行收縮。因此，可行域的最終形狀很大程度上依賴于算法的參數設置，包括最終節點數量及迭代次數。最終節點數量的推薦值為1[14]，也就是說可行域會隨著迭代盡可能地縮小，這樣的設置不需要任何先驗信息。但是，最終結果會趨向于集中在一個很小的區域上，結合一定的先驗信息設置最終節點數量才能使可行域最終收斂在一個合適的大小上。

由圖2和表1可以看出，所提方法表現優于FCN和OPSR。FCN的結果表明，對于FEM框架下的BLT重建，由于FEM網格的不規則性，直接訓練端到端的全連接神經網絡很難取得較好的效果。所提方法和FCN的差別能夠解釋這種表現上的差異，其使用神經網絡實現光子密度分布的補全，而非直接端到端的重建出光源分布。光源分布和光子密度分布的區別在于分布的形式不同，前者具有明確的邊界，是一個分片連續的函數且包含大量的零值，后者則是一個連續函數且沒有零值。相比稀疏的分片連續函數，連續函數受到網格不規則性的影響更弱。此外，結果表明網格拓撲層能夠改善網絡的性能，其模擬了光子密度分布的補全應該是一個由外向內逐步遞進的過程。

與傳統迭代法相比，基于深度學習的BLT圖像重建方法在計算效率方面表現卓越。如表2所示，基于深度學習的兩種方法重建一副圖像只需不到1 ms的時間，而作為迭代法的OPSR則需要超過10 s，OPSR的大量耗時主要源于必不可少的迭代過程。相比之下，基于深度學習的方法只需要將測量數據輸入至神經網絡，神經網絡的預測過程則只需要若干次矩陣乘法即可完成，這樣不僅計算效率極高，且可以同時饋送多組測量數據進行同時計算。深度學習的這種計算高效性，源于其預測時較低的時間復雜度。與迭代法不同，深度學習的預測過程僅由若干個矩陣乘法組成，而不存在求逆過程，也不需要計算梯度，降低了計算的時間復雜度。但是，深度學習的網絡模型通常較大，需要存儲大量的權重參數，因此較迭代法具有更高的空間復雜度。

此外，還對初始化、初始學習率以及NFCL等3種因素對網絡性能的影響進行了測試，結果如圖3所示。初始化的測試通過重復4次訓練過程實現，結果如圖3(a)所示，權重值的初始值由正態分布確定，因此每次訓練都具有不同的初始化。初始學習率的測試中分別測試了10-6、10-5、10-4和10-3等4種不同初始學習率下的網絡性能，結果如圖3(b)所示。NFCL的測試中分別為網格拓撲層接續了1～5層的全連接層，結果如圖3(c)所示。

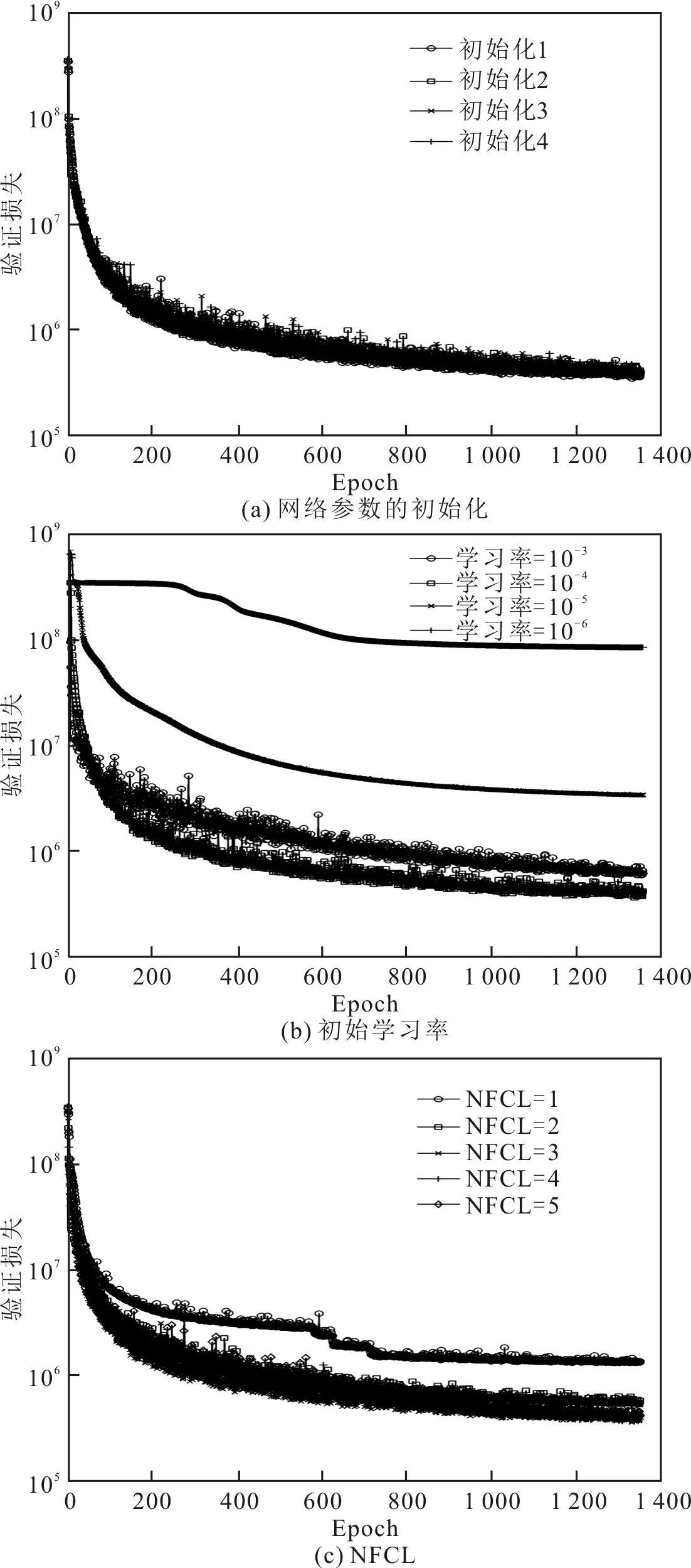
圖3 初始化、初始學習率以及NFCL對網絡性能的影響

神經網絡的訓練是深度學習的關鍵步驟，一個神經網絡的表現很大程度上取決于訓練數據集和訓練策略。對于BLT，基于FEM的擴散方程求解長久以來被廣泛用于模擬仿真和圖像重建。FEM的高效計算特性適應深度學習對大規模數據和頻繁訓練場景的需求。對于訓練策略，作者測試了3種可能會影響網絡性能的因素。如圖3(a)所示，網絡參數的初始化對網絡性能的影響非常微弱，不同初始化的驗證損失基本上變化一致。圖3(b)顯示，初始學習率會顯著影響網絡性能，一個較大的初始學習率會導致過早的訓練停滯，而一個較小的初始學習率會降低收斂速度，初始學習率為10-4時會帶來最好的網絡性能。圖3(c)表明，3個全連接層能夠充分應付當前數據集的訓練，少于3個全連接層會導致網絡性能的明顯降低，而大于3個全連接層基本上不會帶來性能的提升但會增加訓練時間。

利用有限元方法產生訓練樣本可以快速產生大量訓練樣本。空間域固定，則K就是固定的，對于不同的樣本僅需計算一次，只要設計不同的X分布即可同時獲得大量樣本。而利用蒙特卡洛方法產生訓練樣本，每個樣本都需要進行獨立的光子輸運模擬，計算時間會隨著樣本數的增加成倍增長。利用有限元方法產生訓練樣本的缺陷是有限元的計算精度與網格的細分程度直接相關，網格越精細，則計算的精度越高，但網格密度的提升會同時增大神經網絡的規模，將會增加網絡訓練的難度。目前，神經網絡的快速訓練依賴于圖形處理器(Graphics Processing Unit,GPU)加速，而GPU的顯存容量有明確的界限，限制了單顯示卡下所能訓練的網絡規模，間接限制了有限元網格的精細化程度。分布式計算能夠在一定程度上解決該問題，但其計算效率提升不如單顯示卡訓練，并且會增加硬件成本。

4 結 語

提出一種基于FEM和深度學習的BLT圖像重建方法。該方法使用FEM求解擴散方程生成數據集，采用一種由網格拓撲層和全連接層組成的神經網絡，通過該神經網絡實現光子密度分布的補全，而非構造直接端到端的圖像重建。在獲取完整的光子密度分布后，再通過將剛度矩陣與光子密度向量相乘獲得生物發光光源分布。仿真實驗結果表明，所提方法的表現優于直接端到端的FCN和基于可行域的迭代法OPSR。