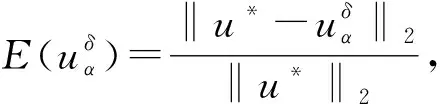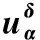初始場與邊界熱流同時識別反問題的正則化方法
趙宇星, 徐定華
(浙江理工大學 理學院, 杭州 310018)
熱傳遞規律廣泛應用于目標體識別、 智能設計與制造領域, 如高爐煉鋼、 熱防護服設計、 機器制造等[1-2]. 該類問題的共性特點是通過熱傳導方程描述熱傳遞現象, 給定初始溫度分布和邊界溫度場, 研究區域內部溫度場的分布. 這類熱傳導方程定解問題在數學上通常稱為正問題.
熱傳導方程反問題在識別、 控制、 設計等領域應用廣泛[3-4]. 文獻[5-6]用Fourier正則化方法研究了熱傳導反問題的數值解法; 文獻[7]給出了無初始值的逆時熱傳導反問題的數值方法; 文獻[8]基于直接和伴隨模型方程的迭代提出了一種求解傳熱反問題的算法, 使擬合泛函最小化; 文獻[9]利用同倫攝動方法研究了含Neumann邊界條件的熱傳導反問題; 文獻[10-11]研究了熱傳導反問題轉化為Fredholm積分方程系統的Tikhonov正則化理論.
本文考慮一維Neumann邊界條件的熱傳導方程:
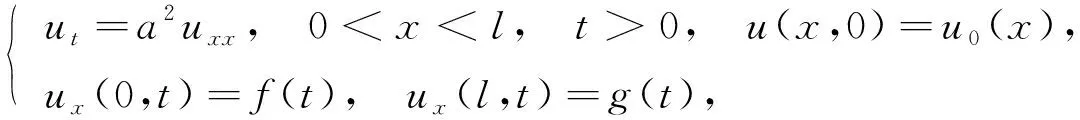
(1)
其中a2為熱傳導系數.{u0(x),f(t),g(t)}均已知的熱傳導定解問題(1), 稱為正問題.本文討論g(t)已知, 但{u0(x),f(t)}均未知且需確定的反問題.
反問題(IP): 利用測量的右端溫度值u(l,t)|t∈[0,T]和終止時刻溫度值u(x,T)|x∈[0,l], 給定g(t)|x∈(0,T], 由系統(1)確定{u0(x),f(t)}.
文獻[7]利用右邊界溫度值的一組數據確定兩個未知函數{u0(x),f(t)}, 因不具備唯一性, 故經對未知的f(t)給定先驗性約束條件(即f(t)滿足對稱性)可使其滿足唯一性.本文利用兩組數據可同時反演出左邊界熱流密度與初始溫度, 而不需要對解進行對稱性先驗約束.本文首先將反問題(IP)轉化為不適定的第一類Fredholm積分方程組, 離散為兩個病態線性方程組, 分別采用改進的Tikhonov正則化方法和BV(bounded variation)正則化方法求解連續解與非連續解; 其次, 針對誤差較大的數據, 采用多次重復測量及預處理方法提高數據精度, 再經正則化方法反演初始值和邊界值, 從而獲得滿足精度要求的近似解; 最后通過數值算例驗證算法的有效性.
1 反問題(IP)的唯一性
1.1 反問題(IP)轉化為Fredholm積分方程組
針對含Neumann邊界條件的熱傳導方程定解問題, 給定右端溫度值u(l,t)|t∈[0,T]和終止時刻溫度值u(x,T)|x∈[0,l], 需同時反演初始溫度u0(x)和左邊界熱流密度f(t).
文獻[12]給出了正問題(1)的解:

(2)
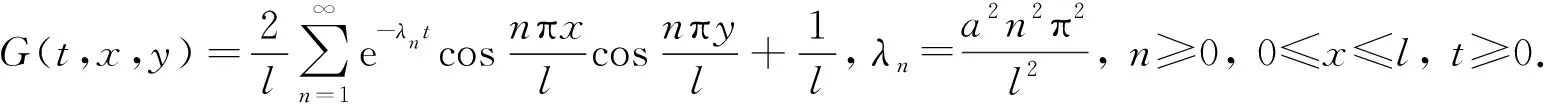
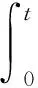

(3)
分別將x=l和t=T代入式(3)可得Fredholm積分方程組:
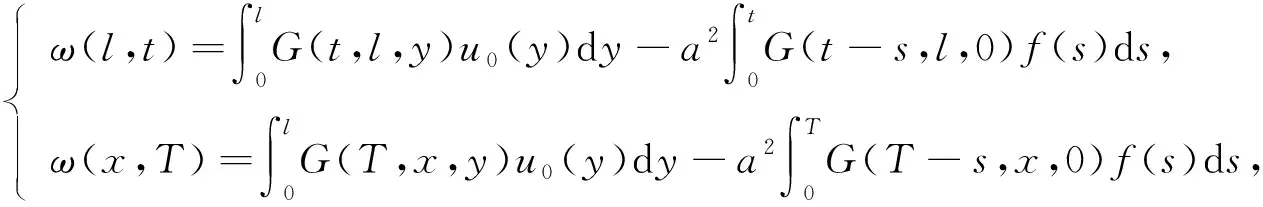
(4)
其中0≤x≤l, 0≤t≤T,
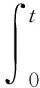

由上述推導可知, 反問題(IP)與方程組(4)等價.
1.2 唯一性
定理1設u0(x)∈L2[0,l],f(t)∈L2[0,T], 則反問題(IP)的解u0(x)和f(t)必唯一.
證明: 設方程組(4)有兩組不同的解, 分別為(u0,1(x),f1(t))和(u0,2(x),f2(t)).記U(x)=u0,1(x)-u0,2(x),F(t)=f1(t)-f2(t), 則可得積分方程組:
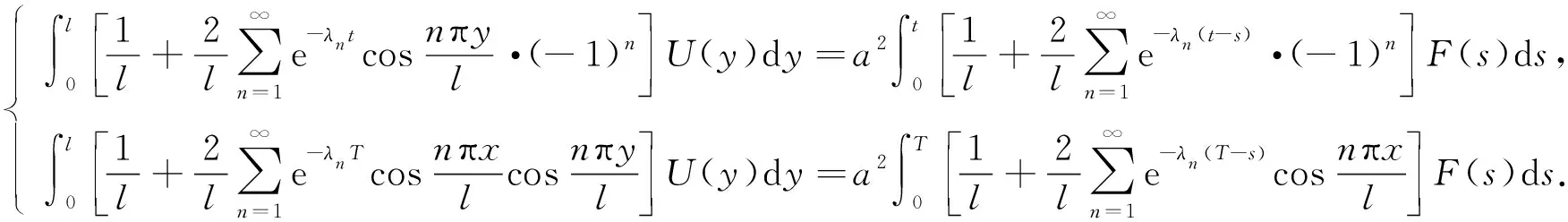
(5)
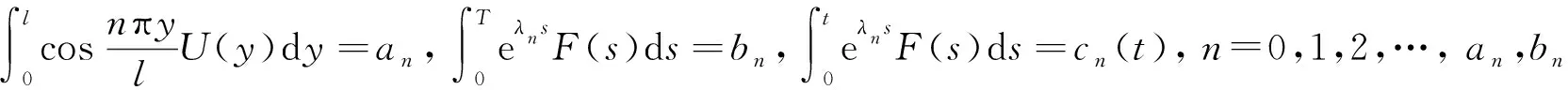
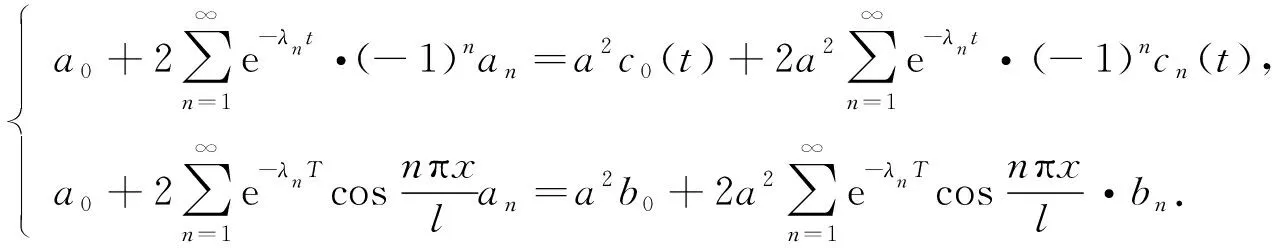
(6)
將方程組(6)的第二個方程進行移項, 并化簡整理可得
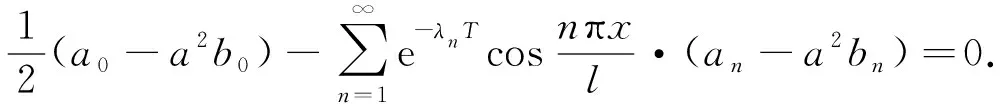
(7)

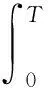
代入方程組(6)的第一個方程, 化簡為
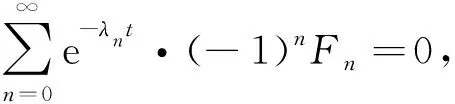
(8)
其中
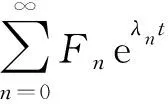
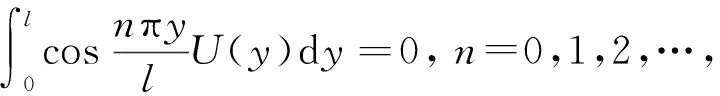
注1相比于文獻[7], 本文不需要對解進行對稱性先驗約束, 而是通過另外測量的終止時刻溫度值u(x,T)|x∈[0,l]構成方程組, 保證了反問題(IP)解的唯一性.
2 反問題(IP)的數值算法
2.1 離散格式及不穩定性
取a=1, 則方程組(4)變形為
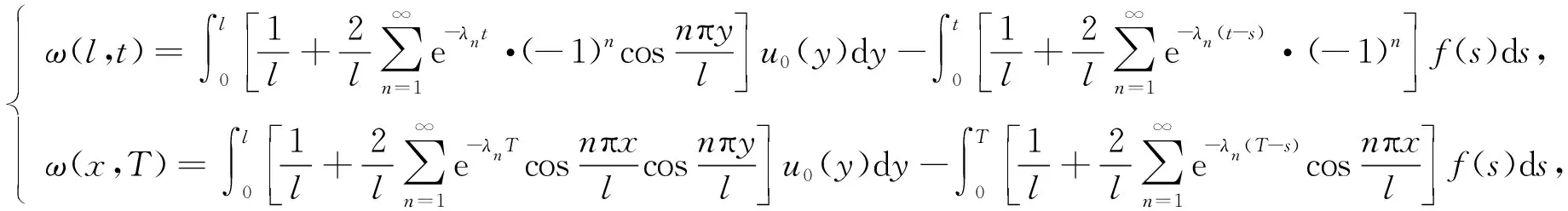
(9)
其中0≤x≤l, 0≤t≤T.
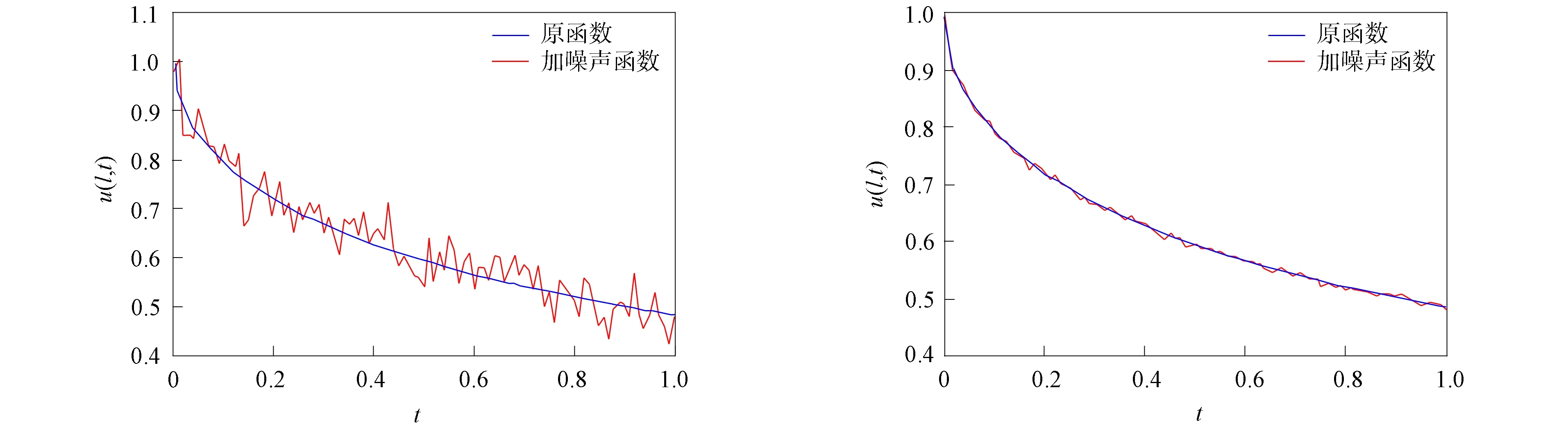
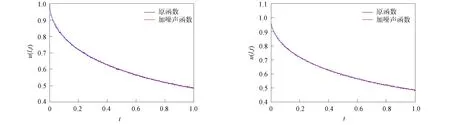
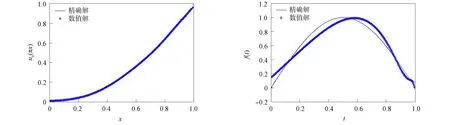
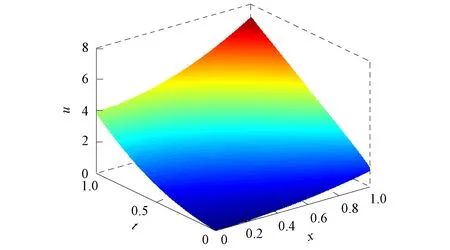
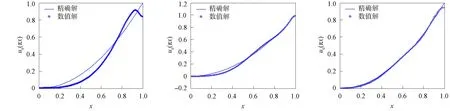
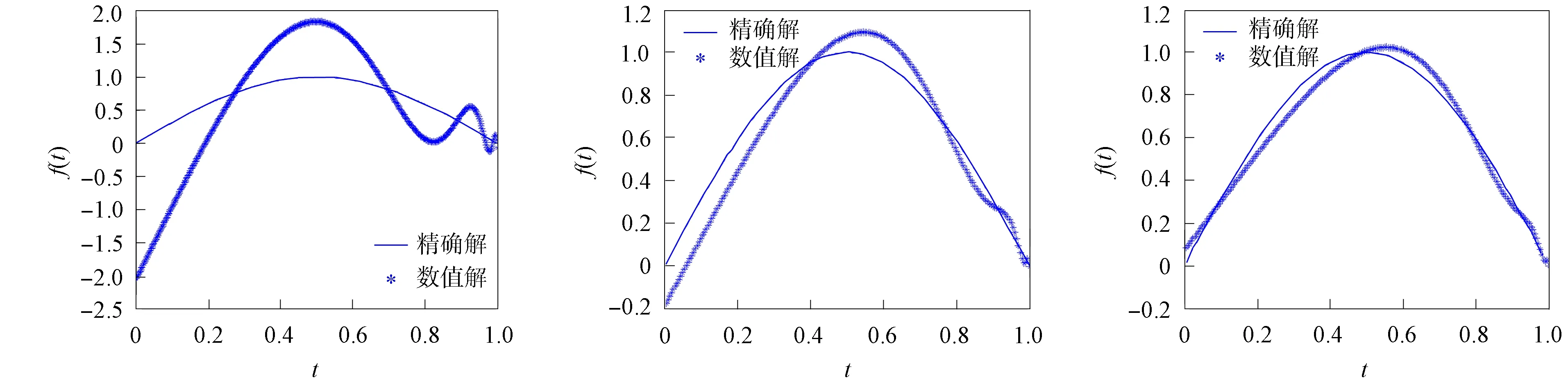
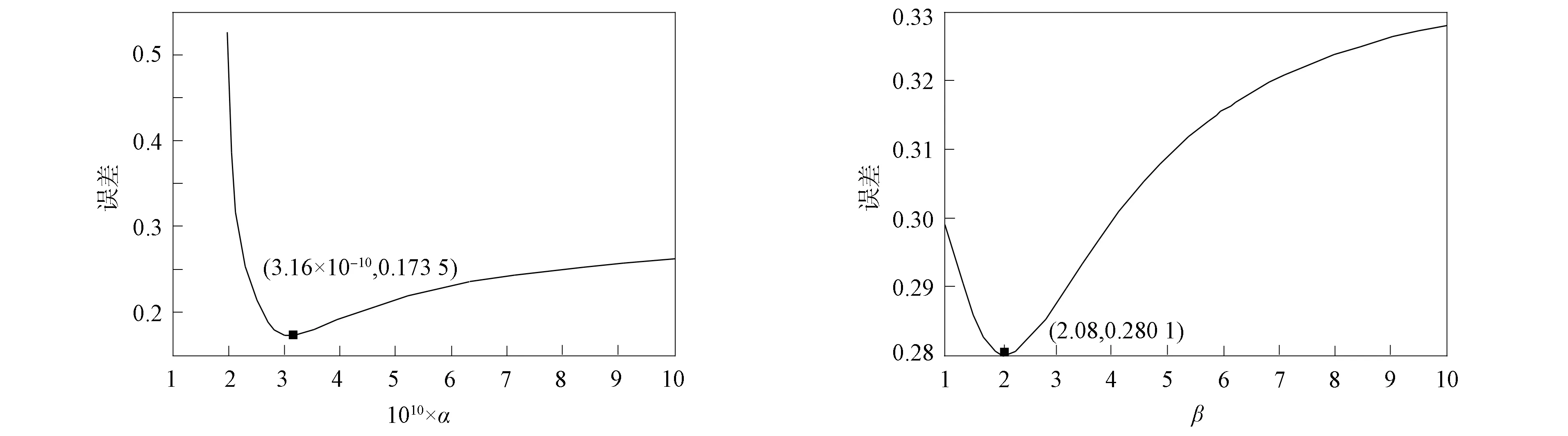
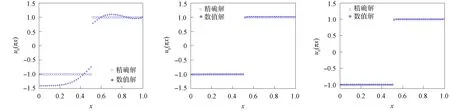
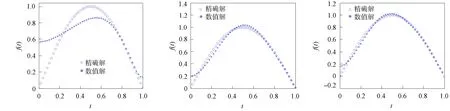
將方程組(9)中的核函數依次記為K1(t,y),K2(t,s),K3(x,y),K4(x,s), 當t 2) 利用矩形求積公式對方程組(9)中的積分進行數值求積: (10) 記 u=(u0(yj))n×1,f=(f(sj))n×1,A=(K1(ti,yj)Δy)n×n,B=(K2(ti,sj)Δs)n×n, C=(K3(xi,yj)Δy)n×n,D=(K4(xi,sj)Δs)n×n,M=(ω(l,ti))n×1,L=(ω(xi,T))n×1, 則方程組(10)的矩陣形式為 (11) 經計算當n=50時, 矩陣A,C,D的條件數均處于1018的數量級, 且節點選取越多, 矩陣A,C,D病態程度越嚴重, 可見反問題(IP)的不穩定性.觀察到矩陣B為滿秩的可逆良態矩陣, 因此可先處理矩陣B, 對方程(11)進行“消元”消去向量f, 得到關于向量u的方程: Ku=G, (12) 其中K=DB-1A-C,G=DB-1M-L.易知, 矩陣K的病態程度較嚴重, 需使用穩定化方法求解方程(12). 2.2 改進的Tikhonov正則化 對方程Ku=G利用Tikhonov正則化方法求解連續函數u0(x)在節點處的近似值.方程(12)的正則化解是Tikhonov泛函的極小值, 用緊算子的奇異值系統可表示為 (13) 本文采用文獻[13]提出的改進正則化濾波函數: (14) (15) 2.3 BV正則化 當u0(x)不屬于連續函數空間時, 本文用BV正則化方法將其轉化為非線性最優化問題. TV(total variation)正則化方法是求解 (16) 本文利用一個光滑泛函逼近TV(u0), 加參數β>0得到穩定泛函, 此時全變差泛函對應的非線性優化反問題表示為 (17) 該方法通常稱為BV正則化算法[14]. 為方便數值模擬, 將計算區域劃分為[0,1]×[0,1]的網格.考慮u0(πx)=x2,f(t)=sin(πt),g(t)=2πcos(πt), 利用中心差商[15]對正問題(1)進行離散.正問題(1)的數值解如圖1所示.在下面反問題的計算中, 將正問題的結果賦予加性噪聲后作為反問題的測量數據進行數值模擬. 圖1 正問題(1)的數值解u(x,t)Fig.1 Numerical solution u(x,t) of direct problem (1) 例1考慮精確解u0(πx)=x2,f(t)=sin(πt).誤差水平δ分別為5%,1%,0.1%, 用改進的Tikhonov正則化方法得到數值解, 參考文獻[13]取r=1.5,σ=4, 先驗選取的正則化參數α=δ6/7, 反演后的初始值如圖2所示, 反演后的左邊界值如圖3所示.由圖2和圖3可見, 隨著測量數據誤差的減小, 反演效果逐漸增強.當誤差水平為5%時, 反演效果不理想. 圖2 不同誤差水平下單次測量反演初始值Fig.2 Initial values inversion via single measurement under different error levels 圖3 不同誤差水平下單次測量反演左邊界值Fig.3 Left boundary values inversion via single measurement under different error levels 步驟1) 固定正則化參數α=αi, 得到關于β和誤差err的圖像, 其最低點坐標為(βi,erri); 固定βi, 得到關于α和誤差err的圖像, 其最低點坐標為(αi+1,erri+1),i=0,1,2,…,n; 步驟2) 給定ε=10-9, 當erri+1 圖4 最優正則化參數Fig.4 Optimal regularization parameters 根據上述方法選取的最優參數利用BV正則化方法反演后的初始值如圖5所示, 反演后的左邊界值如圖6所示. 由圖5和圖6可見, 隨著測量數據誤差的減小, 反演效果逐漸增強. 圖5 不同誤差水平下多次測量反演初始值Fig.5 Initial values inversion via multiple measurements under different error levels 圖6 不同誤差水平下多次測量反演左邊界值Fig.6 Left boundary values inversion via multiple measurements under different error levels 求解 得到的f*,N即為經過預處理后提高了精度的數據, 最后再利用改進的Tikhonov正則化方法求解. 在誤差水平為5%和1%的情形下, 加噪聲函數與原函數擬合的對比結果如圖7所示.圖7顯示了數據預處理的必要性.圖8為經過數據預處理后得到的函數(σ2=0.001 6,N=30). 由圖8可見, 數據預處理為增強反演效果提供了高精度的數據. 圖7 不同誤差水平下原函數與加噪聲函數的對比結果Fig.7 Comparison results between original function and noisy function under different error levels 圖8 不同誤差水平下的數據預處理結果Fig.8 Data preprocessing results under different error levels 參考文獻[16], 選取最優的正則化參數, 在誤差水平為5%的情形下, 經過數據預處理后反演得到的初始值和左邊界值如圖9所示; 在誤差水平為1%的情形下, 經過數據預處理后反演得到的初始值和左邊界值如圖10所示. 本文不考慮誤差為0.1%的情形, 因為此時誤差較小, 若進行數據預處理則會增加計算成本. 圖9 在誤差水平為5%情形下的雙函數反演Fig.9 Double function inversion with error level of 5% 圖10 在誤差水平為1%情形下的雙函數反演Fig.10 Double function inversion with error level of 1% 表1 近似解和的相對誤差 綜上, 本文討論了含Neumann邊界條件的熱方程定解問題. 首先, 給定右端溫度值和終止時刻溫度值, 確定初始值和左邊界值的反問題. 通過建立Fredholm積分方程組, 證明了反問題(IP)解的唯一性, 并利用改進Tikhonov正則化算法和BV正則化算法反演了初始值和左邊界值; 其次, 本文對誤差較大的數據先進行預處理再進行正則化; 最后, 借助MATLAB數學軟件進行了數值模擬. 對于Robin邊界條件, 該條件可以刻畫邊界有熱交換的情況. 針對高維問題, 由于數據本身的復雜性及測量時不可避免的誤差, 更需進行數據的預處理, 從而得到高精度的數據便于進行函數反演.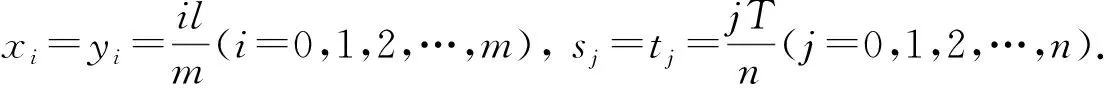
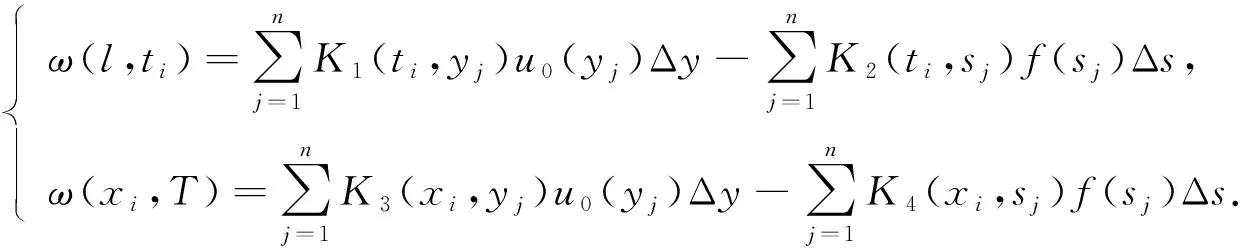
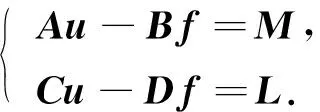
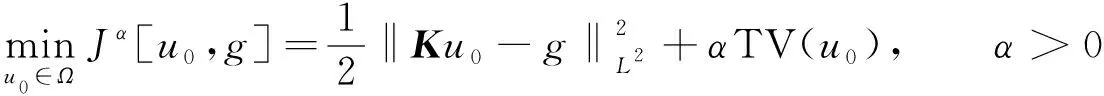

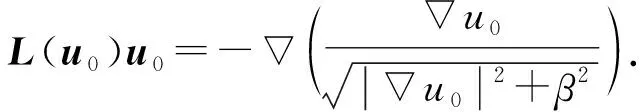
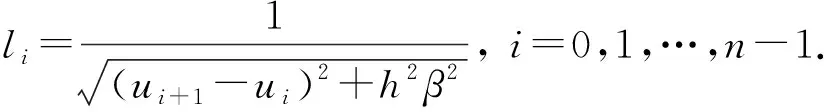
3 數值實例
3.1 連續函數重構
3.2 不連續函數重構
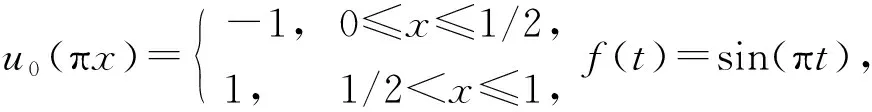
3.3 基于重復測量數據的函數重構