基于循環神經網絡的微地震數據降噪方法

李盼池, 石 彤, 李學貴

(東北石油大學 計算機與信息技術學院, 黑龍江 大慶 163318)

微地震是在開采井附近的巖體因應力場變化導致巖石破裂引起的微小地震事件, 微地震事件監測中檢波器收集的微地震信號因易受周圍環境的影響常含有大量噪聲, 而含噪微地震數據會導致微地震信號識別困難, 影響微地震后續研究的準確性及可靠性. 因此, 進行微地震監測首先要對微地震數據進行降噪處理.

針對檢波器采集到的微地震信號存在噪聲的問題, 目前已有許多處理方法. 刁瑞等[1]采用負熵作為目標函數, 通過引入粒子群優化算法提高求解效率, 利用互相關系數處理盲源分離的不確定性問題, 有效實現了微地震數據降噪； 慕陽等[2]在實驗中采用提取最優小波基, 確定分解層數及對分解信號設置合適閥值等步驟消除部分噪聲, 實現了提高微地震信號信噪比的目的； 王亞娟等[3]提出了將含噪數據進行集成經驗模態分解, 計算不同頻率的本征模態函數(intrinsic modal function, IMF)樣本熵, 設置樣本熵閾值提取符合微震信號特征的IMF分量并對其進行信號重構, 從而抑制隨機噪聲; 弓震等[4]提出了通過學習訓練大量微震資料, 構建可最大化稀疏表示微地震數據的超完備字典, 利用微地震信號與噪聲在訓練字典下的差異, 分離有效信號與噪聲, 最終達到降噪的目的; 王飛等[5]提出了將同步壓縮小波變換技術與自適應閾值處理技術相結合的方法對微地震數據實施降噪處理, 大幅度提高了微地震事件的信噪比; 邵婕等[6]首先利用正交匹配追蹤算法計算多分量數據的稀疏表示, 然后在根據信號特征選擇稀疏變換矩陣的同時根據噪聲方差選擇恰當閾值, 最后通過迭代, 重構誤差直至其小于設定閾值, 從而實現微地震數據降噪; 劉利強[7]提出了首先獲得極小、 極大值包絡線, 然后將原始信號分解為多個滿足條件的信號序列, 最后根據信號特征選取高信噪比的信號序列重構信號的方法實現微地震數據降噪.

普通循環神經網絡(recurrent neural network, RNN)訓練過程中易出現梯度消失與梯度爆炸的問題, 為解決這類問題, Hochreiter等[8]提出了長短時記憶單元(long short-term memory, LSTM)方法. 近年來, 隨著深度學習研究的不斷發展, 其已廣泛應用于信號降噪等問題中. 許滔滔等[9]提出了一種基于LSTM的循環神經網絡, 將其用于對大地電磁工頻干擾壓制, 首先構建基于LSTM循環神經網絡模型, 然后將含噪數據及工頻噪聲分別作為模型的輸入與輸出, 最后獲得輸入與輸出的差值作為降噪后的真實信號, 該方法取得了較好的降噪效果; Shen等[10]在引力波信號噪聲壓制中使用了基于LSTM的循環神經網絡降噪模型, 利用該模型能有效去除隨機噪聲, 且降噪效果比傳統方法優越. 此外, 還有利用LSTM的變體門控循環單元(gated recurrent unit, GRU)構建網絡模型進行降噪的方法[11]. 周澤南[12]將卷積神經網絡與GRU相結合, 并將其作為后續構建循環神經網絡的重要單元, 與基于LSTM的循環神經網絡及傳統濾波方法相比, 該方法在去除InSAR圖像的相位噪聲方面效果明顯.

在目前的微地震數據降噪方法中, 利用深度學習技術降噪的方法較少, 且傳統方法均存在一些缺點, 如小波降噪中若支集長度太大則不利于實時性, 需要精準調參的問題等. 針對微地震信號的時序特性以及傳統方法存在的不足, 本文構建深度雙向門控循環單元循環神經網絡(deep bidirectional gated recurrent unit recurrent neural network, DBGRU-RNN), 并將其應用于微地震數據降噪. 實驗結果驗證了DBGRU-RNN在微地震信號降噪中應用的可行性.

1 循環神經網絡概述

1.1 循環神經網絡

循環神經網絡是一種特殊的神經網絡結構, 表現為RNN會對之前時刻的信息進行記憶并應用于當前輸出的計算中, 即隱藏層之間的節點有連接, 并且當前時刻隱藏層的輸入不僅包括當前時刻的輸入還包括上一時刻隱藏層的輸出[13]. 其網絡結構[14]如圖1所示. 輸入輸出關系表示為

圖1 循環神經網絡結構Fig.1 Recurrent neural network structure

其中t-1,t,t+1為時間序列,x為當前輸入樣本,s0為初始記憶,st為輸入樣本在時間t處的記憶,W為前一時刻隱藏層輸出的權重,U為當前時刻輸入樣本的權重,V為輸出的樣本權重,f和g為激活函數.

RNN在每步輸入、 輸出、 隱狀態的連接中均共享參數, 這種共享機制可顯著降低模型復雜度, 縮短訓練時長, 還能保持較高的精度. 因此, RNN在含有時序數據的任務中有較強優勢.

1.2 門控循環單元

普通RNN訓練時, 經常會出現梯度消失和梯度爆炸的問題, 因此文獻[15]提出了LSTM解決該問題, 其在普通RNN單元的基礎上, 增加了3個可以使信息選擇式通過的門控制信息的量, 從而使梯度值保持穩定, 便于訓練, 但由于加入了門控機制而導致計算復雜度增高. GRU是LSTM的一種變體, 因此, 其使用門控機制學習長期依賴關系的基本思想與LSTM一致. 與LSTM相比, GRU的結構簡單, 計算復雜度低, 且沒有LSTM網絡中內部狀態和外部狀態的劃分, 而是通過直接在當前網絡的狀態ht和上一時刻網絡的狀態ht-1之間添加一個線性的依賴關系, 解決梯度消失和梯度爆炸的問題.其基本單元結構[16]如圖2所示.

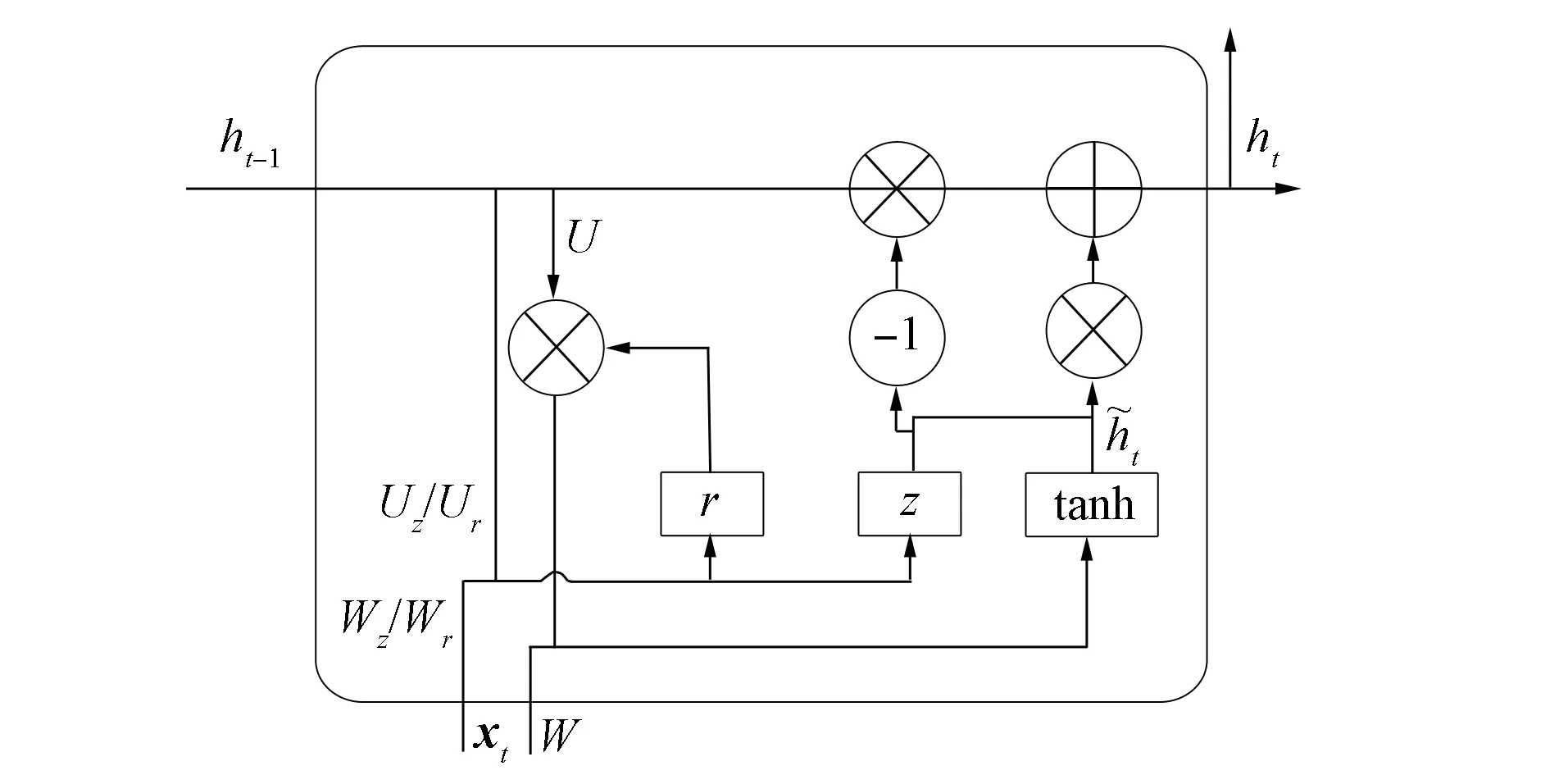
圖2 單個GRU單元基本結構Fig.2 Basic structure of single GRU unit

在經典的GRU模型中, 計算過程[17]分為如下四步：

步驟1) 更新門幫助模型決定前一時刻和當前時刻的信息傳遞量, 其計算公式為

z=σ(Wzxt+Uzht-1+bz);

(2)

步驟2) 重置門決定前一時刻的信息遺忘量, 其計算公式為

r=σ(Wrxt+Urht-1+br)；

(3)

步驟3) 新的記憶內容使用重置門儲存過去相關的信息, 其計算公式為

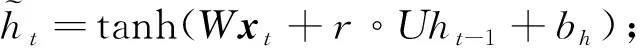
(4)

步驟4) 最后保留當前單元的信息并傳遞到下一個單元中, 其計算公式為

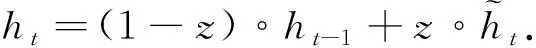
(5)

與LSTM相比, GRU的計算公式簡單, 在具有同等水平數據計算上, 可大幅度提高計算效率. 理論上, 增加循環神經網絡的深度及設置復雜的網絡結構可增強循環神經網絡的能力. 因此, 本文在增加網絡層數的同時還結合了雙向網絡結構, 建立了DBGRU-RNN模型, 與單向GRU相比, 其某時刻的輸出不僅與前一時刻的隱狀態有關, 同時還與后一時刻的隱狀態有關, 因此該模型能利用時序數據的上下文信息進行建模, 獲得比單向GRU更準確的結果[18].

2 基于DBGRU-RNN的微地震降噪方法

本文構建網絡模型時首先考慮到循環神經網絡具有強大的處理序列數據的能力, 且微地震數據為一維序列數據, 提出將循環神經網絡用于微地震數據降噪處理中； 其次考慮到普通循環神經網絡易出現梯度消失等問題, 本文將傳統循環單元替換為門控循環單元； 再次考慮到與單向循環神經網絡相比, 雙向循環神經網絡某時刻的輸出不僅與前一時刻的隱層狀態有關, 同時還與后一時刻的隱層狀態有關, 因此雙向循環神經網絡模型能充分利用時序數據的上下文信息進行建模, 獲得比單向循環神經網絡更準確的結果； 最后考慮到增加神經網絡的深度可增加網絡模型的容錯能力, 提高網絡模型的魯棒性. 因此, 本文選擇深度雙向門控循環單元循環神經網絡用于微地震數據降噪.

2.1 DBGRU-RNN模型

本文構建的DBGRU-RNN模型如圖3所示, 包括3個GRU隱藏層, 由下至上分別為輸入層、 GRU隱藏層和輸出層. 隱藏層中實線表示前向層, 虛線表示反向層. 其中, 3個GRU隱藏層為整個網絡模型的核心部分.

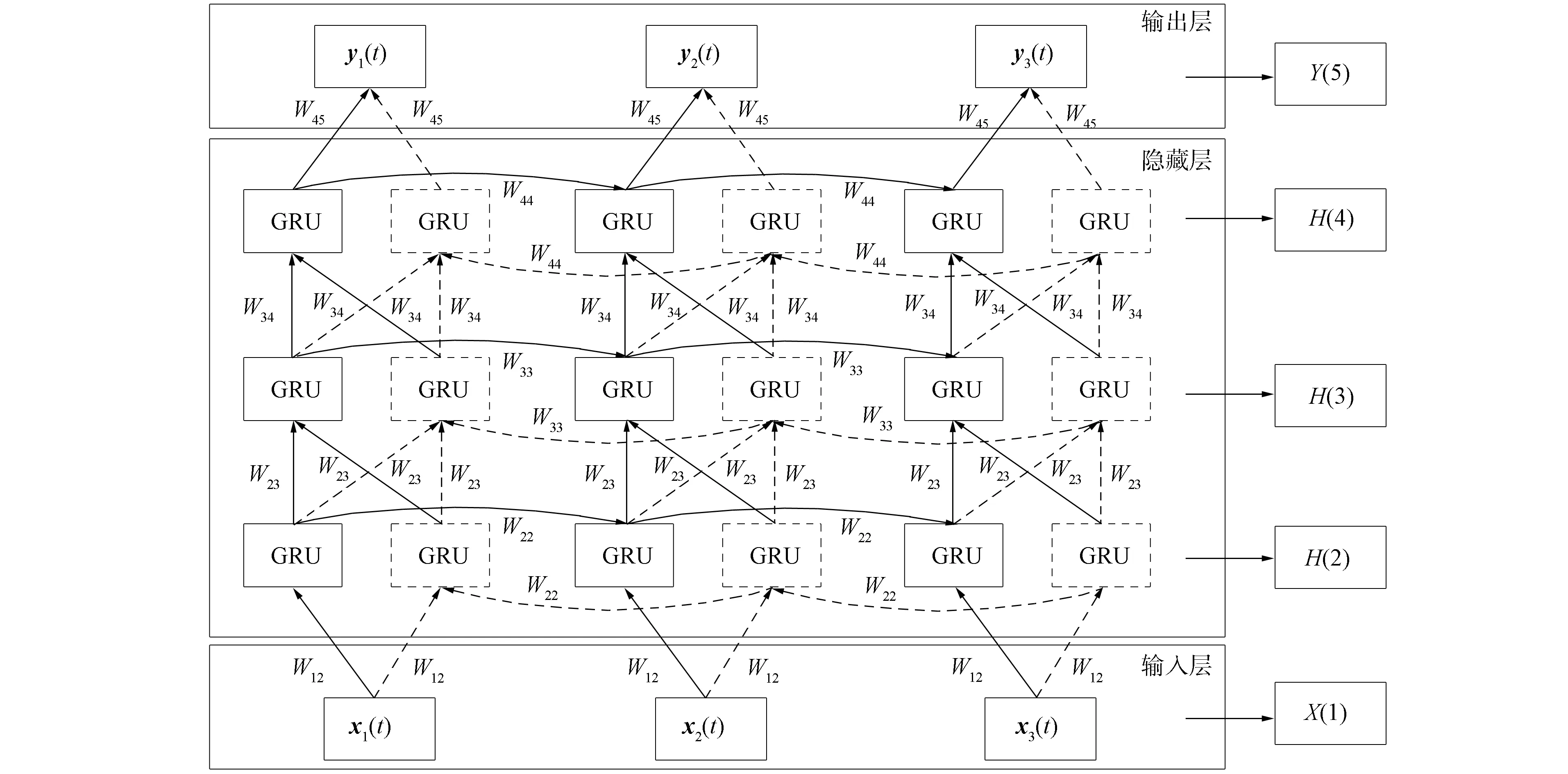
圖3 深度雙向GRU循環神經網絡模型Fig.3 Deep bi-directional GRU-RNN model

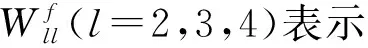
誤差函數定義為

(9)

輸出層權值梯度為

(10)

其中g′為激活函數的導數.令

則

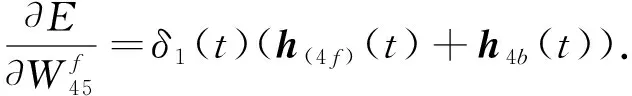
(11)

根據鏈式法則可推出

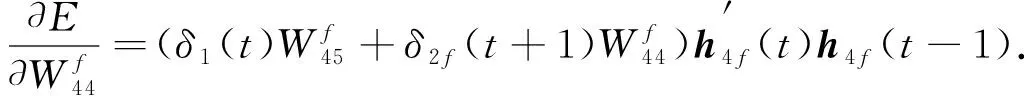
(12)

令

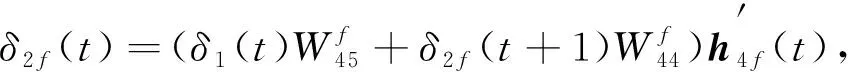
則第三GRU隱層參數梯度可計算為

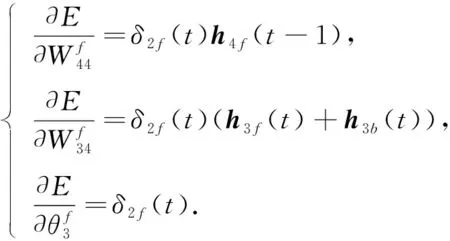
(13)

依次類推, 可得其余各層權值及閾值梯度計算公式為

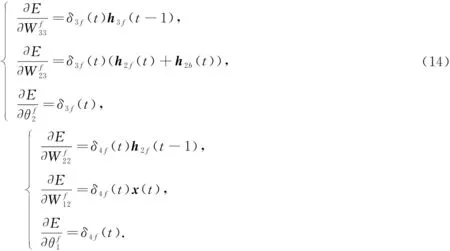
(15)

在DBGRU-RNN網絡模型中, 正向層中各參數調整的公式不相同, 本文按照統一的規則進行調整, 該規則用公式可表達為

β(t+1)=β(t)+αΔβ(t+1),

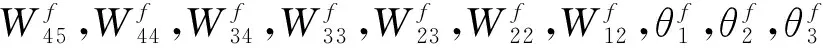
2.2 微地震降噪方法

構建基于DBGRU-RNN的微地震數據降噪方法, 旨在利用該網絡模型訓練到含噪微地震數據與純凈微地震數據間的映射關系. 設X,Y表示純凈微地震數據信號, 則有

Y=F(X+ξ),

(16)

其中F表示構建的網絡模型,ξ表示高斯噪聲.

模型的目標是構建加入噪聲后的微地震數據與純凈微地震數據之間的映射關系, 則輸入實際微地震數據至網絡模型后對應的輸出即為降噪后的信號S, 則S與Y之間的關系可表示為

S=Y.

(17)

2.3 數據預處理及評價指標設置

由于實際中無法獲取到完全純凈的微地震信號以及含噪微地震信號中的噪聲信號, 因此為構建DBGRU-RNN模型訓練時所需的微地震數據集和噪聲數據集, 本文采用Ricker子波正演的方式, 合成微地震信號作為仿真實驗中的純凈數據. 采用高斯噪聲作為噪聲信號, 在純凈微地震信號中加入高斯噪聲作為含噪微地震信號, 含噪微地震信號及純凈數據分別作為輸入輸出樣本數據集. 其中樣本數據集分為兩部分: 一部分為訓練集, 另一部分為驗證集.

在評價基于DBGRU-RNN的微地震降噪方法的性能時, 本文采用4個評估指標進行評估分析, 分別為用于衡量信號是否失真的峰值信噪比PSNR(peak signal-to-noise ratio)[19], 反映一個數據集離散程度的均方差MSE(mean square error), 反映變量之間線性相關程度的相關系數CORC(correlation coefficient)[12]以及反映變量之間相近程度的能量比ER(energy ratio)[20]. 設純凈微地震信號為X, 降噪后微地震信號為Y, 則4個指標的計算公式分別為

其中X與Y越接近, 峰值信噪比越大, 均方差越小, 相關系數及能量比越接近于1.

2.4 仿真測試

本文使用MATLAB2014進行仿真實驗, 通過在由Ricker子波正演得到的微地震數據信號中加入高斯噪聲模擬含噪信號. 本文共生成48 000道數據, 每道數據采樣點為400, 其中40 000道為訓練集, 8 000道為測試集. 為便于觀察降噪效果, 設置生成微地震數據圖的道數為80. 圖4(A)為純凈微地震數據, 圖4(B)為加入高斯噪聲后的微地震數據.

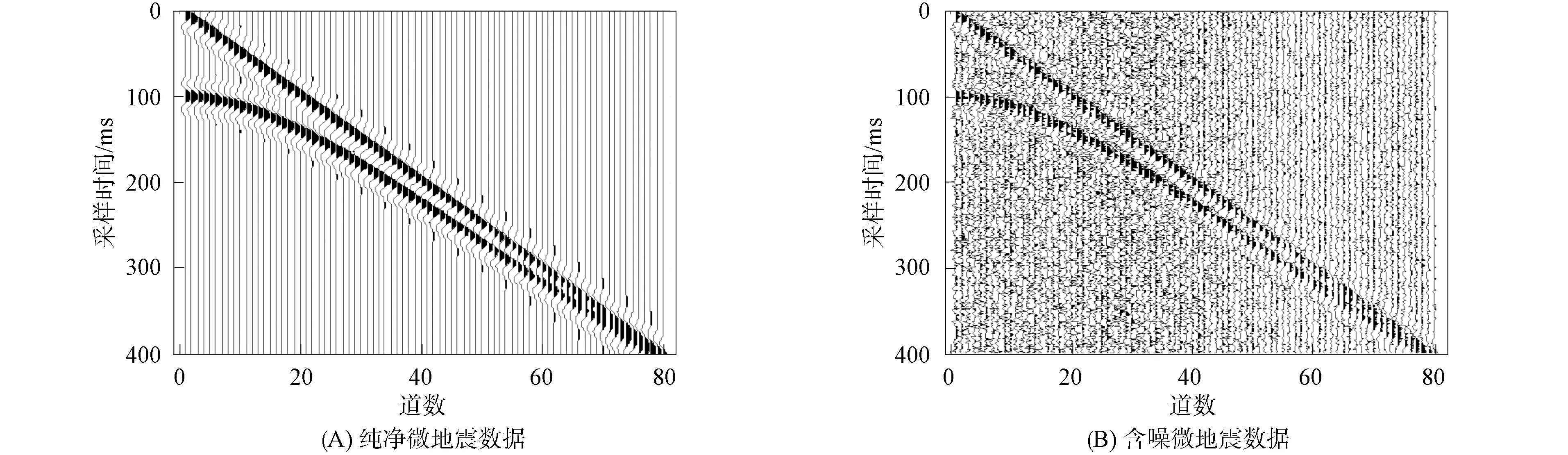
圖4 純凈及含噪微地震數據集Fig.4 Pure and noisy microseismic data sets

本文輸入數據為三維數據, 具體格式為(批量大小,序列長度,輸入層節點), 其中序列長度為每道微地震數據的采樣點數, 即400. 輸入層節點數為每個樣本中的微地震道數, 本文取80. 經過實驗, 批量大小設置為20, 此時樣本共有600/20=30批, 其中訓練樣本25批, 測試樣本5批. 單條樣本的數值列于表1.

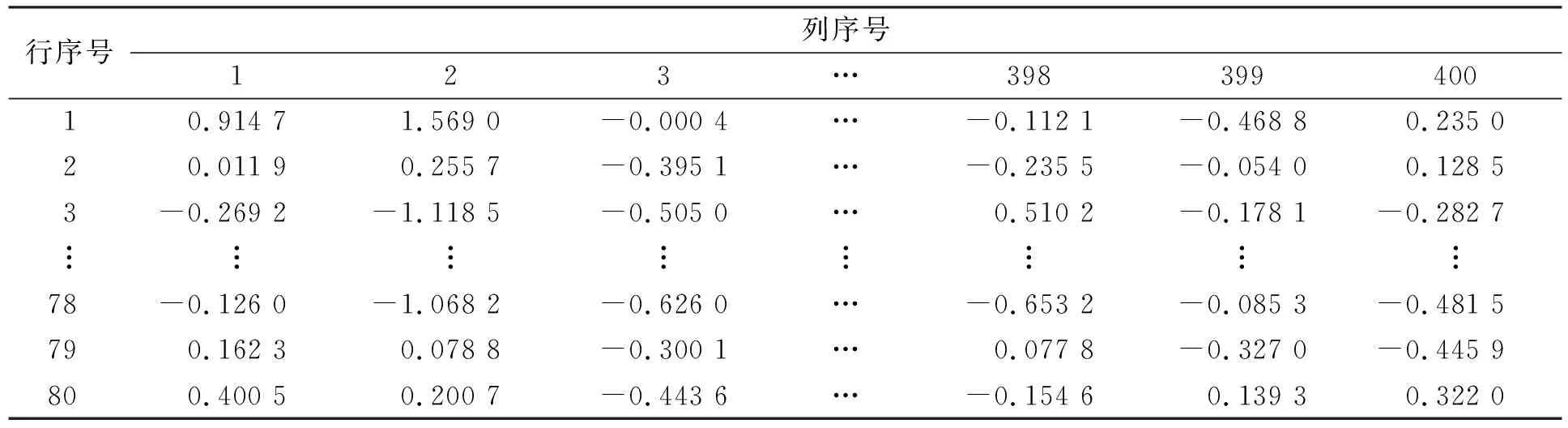
表1 輸入數據示例

網絡參數設置如下： 根據仿真數據并經多次實驗, 網絡的輸入層節點設為80, 3個GRU隱藏層節點設為256,512,512, 輸出層節點設為400, 所有激活函數均采用Sigmod函數. 網絡訓練采用期望輸出與實際輸出之間的均方誤差作為損失函數, 使用Adam優化器在每次迭代過程執行參數調優. 學習率初值設為0.01, 且隨迭代步數按α=0.8α遞減, 學習率最小值限定為10-6. 迭代步數設置為50.

本文采用基于DBGRU-RNN的微地震數據降噪算法, 將其與普通循環神經網絡、 基于LSTM循環神經網絡的降噪算法[21]、 高斯降噪[22]、 BP神經網絡降噪[23]等4種方法同時獨立對含噪微地震信號進行降噪處理, 并對所得結果在降噪波形及評價指標兩方面進行對比分析.

用本文降噪方法與其他4種降噪方法對同一含噪微地震信號進行降噪處理, 其降噪波形結果如圖5所示, 其中： (A)為加入噪聲后的微地震信號； (B)～(F)分別為利用不同方法降噪后的微地震信號.

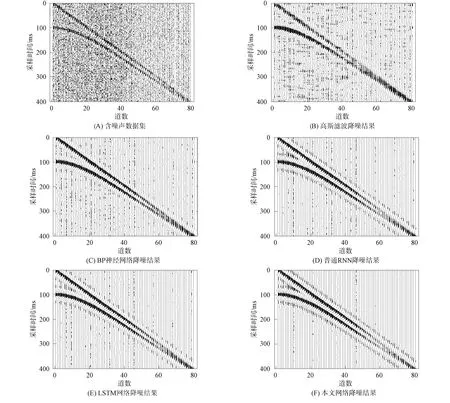
圖5 不同降噪方法對微地震數據的降噪結果Fig.5 Denoising results of different denoising methods on microseismic data

由圖5可見： 圖5(B)為高斯方法降噪后的微地震信號, 與圖4(A)的純凈微地震信號相比, 高斯方法降噪后的微地震信號存在大量噪聲, 有效信號部分被噪聲腐蝕以至于無法識別； 圖5(C)為BP神經網絡降噪后微地震信號, 與圖4(A)的純凈微地震信號相比, BP神經網絡降噪后的微地震信號存在明顯噪聲, 僅有非常少的微地震信號被恢復； 圖5(D)和圖5(E)為普通循環神經網絡及LSTM循環神經網絡降噪后的微地震信號, 可以明顯觀察到噪聲, 與圖4(A)的純凈微地震信號相比, 部分有效信號被恢復； 圖5(F)為本文提出的DBGRU-RNN網絡降噪后的微地震信號, 可見噪聲基本去除, 僅殘留少量噪聲, 有效信號部分可清晰分辨, 與圖4(A)的純凈微地震信號相比波形基本相近. 仿真測試結果表明, 本文提出的DBGRU-RNN降噪方法相比于其他4種降噪方法降噪效果較好.

為明確對比效果, 本文對加入噪聲后的數據分別計算其PSNR,MSE,CORC和ER, 計算結果為: PSNR=1.828 3, MSE=0.656 4, CORC=0.088 6, ER=5.320 9. 5種降噪方法降噪后各評價指標的結果列于表2.

表2 5種降噪方法降噪后各評價指標的結果

由表2可見: 首先, 高斯降噪方法取得的峰值信噪比小于20 dB, 說明該方法的降噪結果失真過大, 得到的結果不可接受; BP神經網絡及普通循環神經網絡降噪方法取得的峰值信噪比大于20 dB, 小于30 dB, 說明得到的降噪效果較差; LSTM循環神經網絡與本文網絡降噪前后相比, 雖然信噪比均大于30 dB, 但結合圖5(E)與圖5(F)所示的微地震信號表明本文網絡得到的降噪效果更好； 其次, 經本文降噪方法處理, 降噪前后信號之間的相關系數值為0.933 5, 說明本文方法處理后的數據與純凈數據基本一致, 而其他方法的相關系數值均低于0.8, 因此與其他4種方法相比, 本文方法的降噪效果最好； 最后, 本文方法降噪前后能量比最接近1, 其他4種方法的能量比均大于本文方法, 進一步說明本文方法降噪后的結果更接近于純凈微地震數據. 利用本文提出的DBGRU-RNN模型降噪后與降噪前微地震信號的峰值信噪比相比約提高36 dB, 且信號之間的相關系數值由0.088 6上升至0.933 5, 能量比最接近于1. 因此, 本文的降噪方法優于其他4種降噪方法.

3 實際應用效果及分析

3.1 礦場資料數據

本文選取大慶油田某井進行水力壓裂時監測的微地震信號作為實測數據, 圖6是截取其中700個采樣點和全部地震道的結果. 由圖6可見, 微地震數據中存在大量的噪聲干擾, 其中第5道和第27道噪聲干擾較大, 無法直接確定微地震信號的位置. 因此, 為更清晰地觀察到微地震信號, 本文隨機選取幾條可明顯觀察到有效微地震信號的地震道進行波形顯示, 如圖7所示.

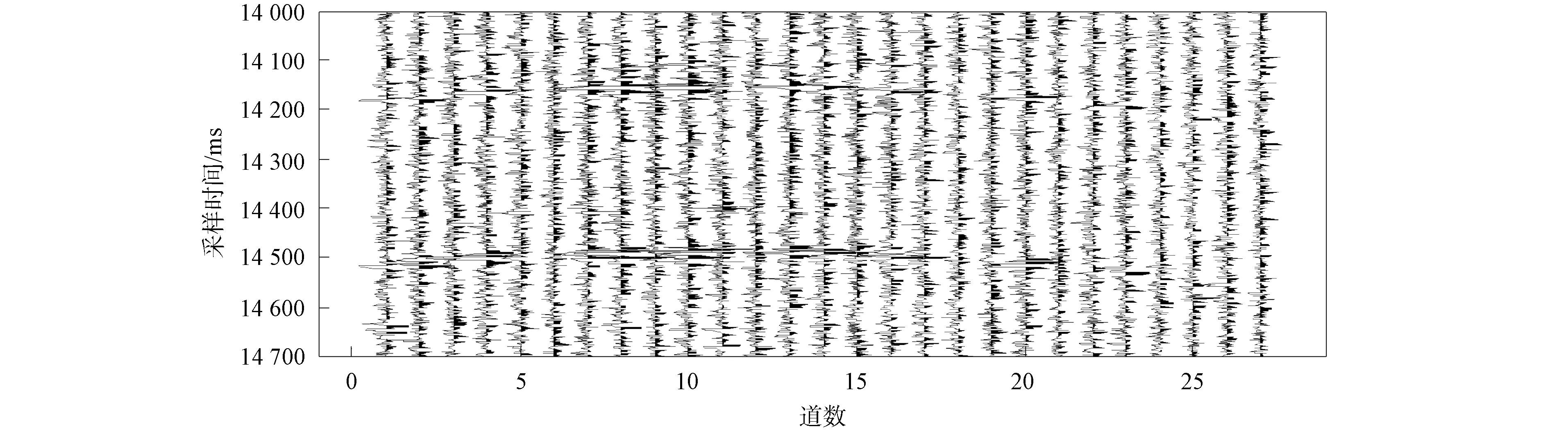
圖6 截取部分微地震信號結果Fig.6 Interception of partial microseismic signal results

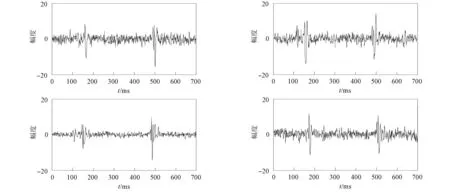
圖7 單道微地震信號Fig.7 Single microseismic signals

3.2 降噪效果及分析

實際微地震數據中存在著大量的噪聲干擾, 其噪聲相比于本文添加的高斯噪聲更復雜, 湮沒了有效的微地震信號. 本文使用DBGRU-RNN網絡模型對實際的微地震數據進行處理, 在對實測數據進行降噪處理過程中, 網絡模型參數仍采用仿真測試中的網絡模型參數進行設置. 為清晰觀察DBGRU-RNN模型的效果, 使用單道微地震數據進行波形分析, 如圖8所示. 由圖8可見， 經本文模型處理后, 消除了部分噪聲信號, 有效微地震信號顯現更清晰.

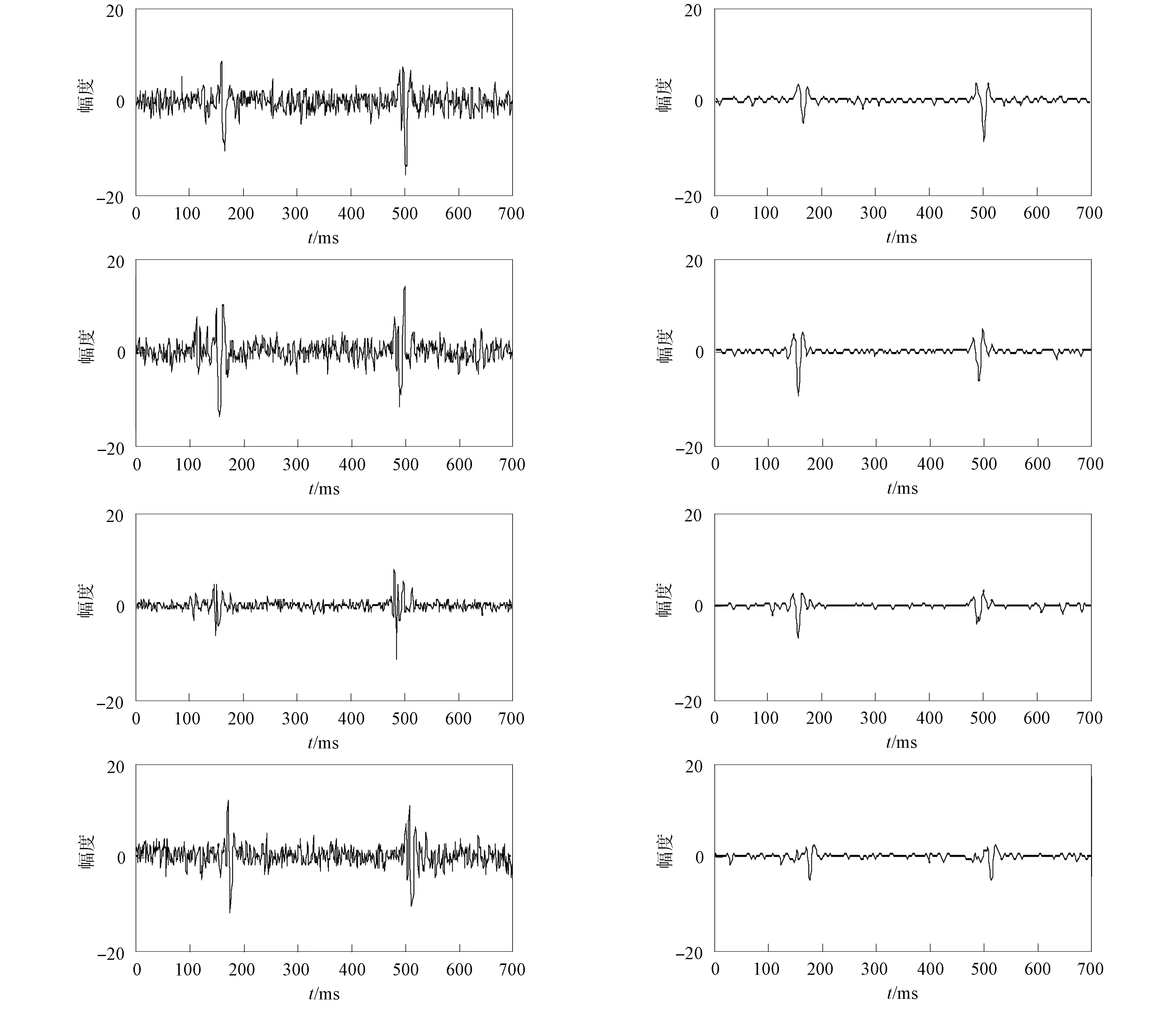
圖8 實測數據降噪結果Fig.8 Denoising results of measured data

為進一步驗證本文網絡模型的有效性, 采用Walsh平均功率法對降噪前后的數據進行功率譜估計, 結果如圖9所示. 為清晰觀察本文網絡模型的降噪效果, 實驗將仿真數據降噪后的功率譜與實測數據降噪后的功率譜進行對比. 圖9中, (A)為仿真含噪微地震數據降噪前功率譜, (B)為仿真含噪微地震數據降噪后功率譜, (C),(E),(G),(I)和(D),(F),(H),(J)分別對應圖7所示4道單道微地震信號降噪前與降噪后功率譜. 由圖9(C),(E),(G),(I)可見, 有效微地震信號均被復雜的噪聲所腐蝕, 無法觀察到有效信號的特征及曲線分布. 由圖9(D),(F),(H),(J)可見, 經本文網絡模型處理后, 有效去除了部分噪聲, 可分辨出有效微地震信號, 并且將圖9(D),(F),(H),(J)所示的功率譜曲線與圖9(B)所示的仿真微地震數據降噪后功率譜曲線進行了對比, 結果表明, 二者的功率譜曲線在總體趨勢上保持一致, 進一步說明本文方法能有效消除微地震數據中的部分噪聲.

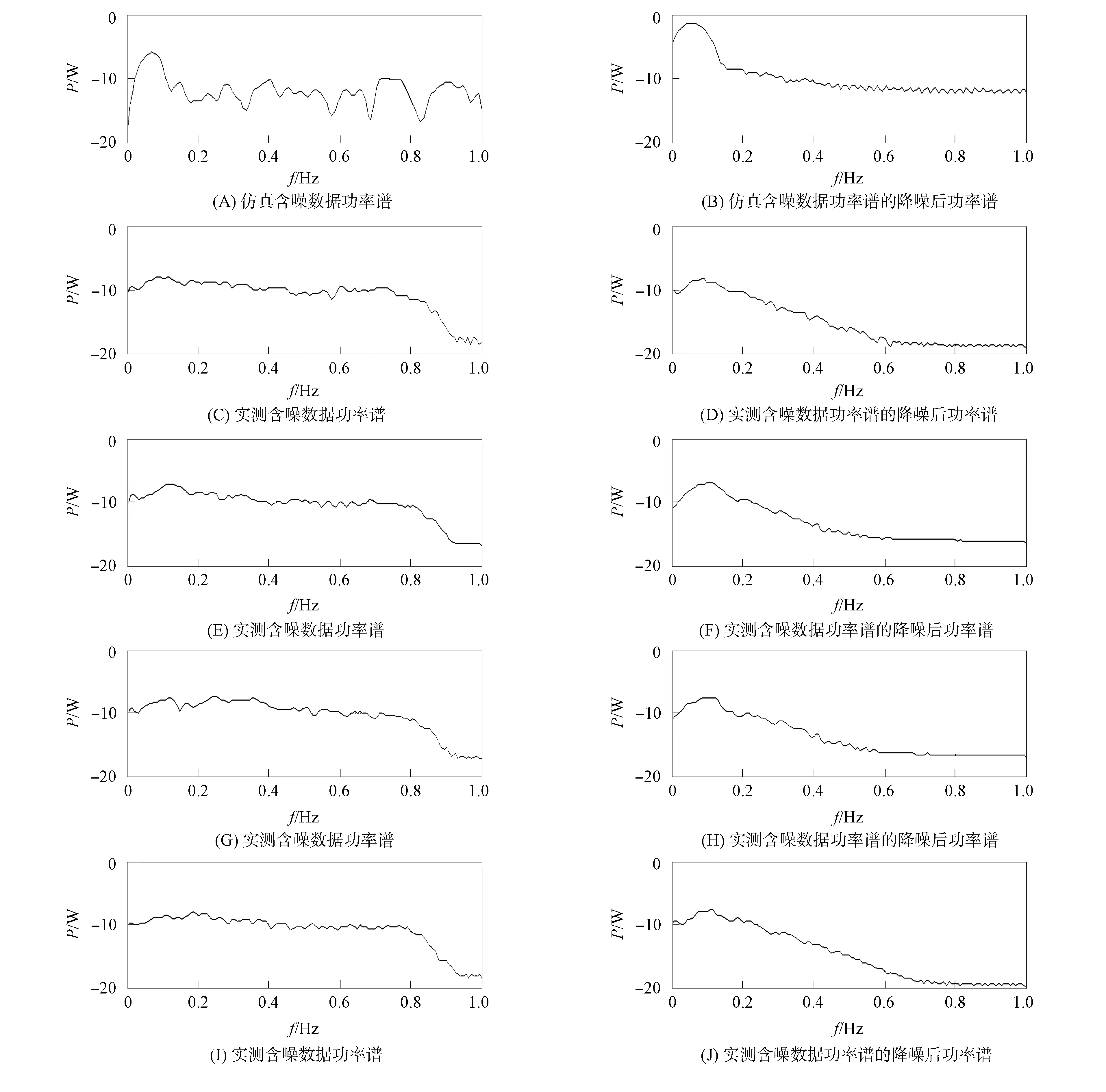
圖9 實測數據降噪前后功率譜對比Fig.9 Power spectrum comparison of measured data before and after denoising

由圖8和圖9可見, 本文方法雖然能有效消除微地震數據中的部分噪聲, 但仍有部分噪聲存在影響微地震信號的識別, 與仿真實驗中得到的結果相比降噪效果較差. 這可能是因為實測數據中噪聲信號極復雜, 而在仿真實驗加入的高斯噪聲無法完全模擬實際噪聲數據所致. 但在計算效率上, DBGRU-RNN比普通循環神經網絡低. 這是因為DBGRU-RNN采用了比普通循環神經網絡更復雜的隱層循環單元以及網絡結構, 這些復雜操作使得DBGRU-RNN模型的性能得以提升.

綜上所述, 本文針對微地震信號中存在大量噪聲干擾, 導致其識別困難的問題, 提出了一種深度雙向門控循環單元循環神經網絡的方法, 并將其應用于微地震數據降噪中. 首先利用Ricker子波正演生成模擬微地震數據集, 采用高斯噪聲作為噪聲數據集, 然后利用構建的數據集驗證本文構建的網絡模型的有效性及準確性, 最后選取4種降噪方法與本文方法進行對比. 仿真實驗結果表明, 本文方法與其他4種方法相比, 降噪效果更好. 進一步, 本文選取大慶油田某井進行水力壓裂時監測的微地震信號作為實測數據, 再次驗證了本文網絡模型的有效性. 由于實測數據中的噪聲極復雜, 而本文仿真實驗中添加的高斯噪聲無法完全模擬實際噪聲, 因此在實際應用中, 雖然本文提出的模型能在噪聲較大的情況下獲得良好的降噪效果, 但仍存在少量噪聲.