改進的Newton-法求解不同階對稱張量組Z-特征值①
楊廷梅, 劉奇龍, 陳震, 許云霞
貴州師范大學 數學科學學院, 貴陽 550025
設R是實數域, Rn是所有n維實向量的集合. 張量是向量和矩陣的高階推廣, 通常m階n維實張量是由nm個實數構成的多維數組, 即
A=(ai1i2…im),ai1i2…im∈R,ij∈N,j∈M
其中N={1, 2, …,n},M={1, 2, …,m}. 記R[m, n]為m階n維實張量的全體構成的集合, 特別地, 當m=0時, R[0, n]簡記為R, 當m=1時, R[1, n]簡記為Rn. 如果實張量A=(ai1i2…im)的元素滿足
aip(1)ip(2)…ip(m)=ai1i2…im,ij∈N,j∈M
p是指標集{1, 2, …,m}上的任意置換, 則稱A是實對稱張量.
文獻[1]提出了張量特征值與特征向量(也稱為張量特征對)的概念, 并討論Z-特征值和H-特征值的一些性質. 張量特征值是矩陣特征值的高階推廣, 下面給出實對稱張量的Z-特征值的定義.
定義1[1]設A∈R[m , n]是實對稱張量, 如果存在λ∈R和非零向量x=(x1, …,xn)∈Rn使得
Axm-1=λx,xTx=1
(1)
則稱λ為A的Z-特征值,x為與λ相對應的Z-特征向量, 或稱(λ,x)是A的Z-特征對, 其中Axm-1是n維向量, 第i個分量為
由于對稱張量Z-特征值在數據挖掘[2-3]、 目標跟蹤[4]和超圖匹配[5]等許多實際問題中有著重要應用, 使得對稱張量Z-特征值問題逐漸成為張量譜理論研究的熱點問題[6-13]. 文獻[14]在研究基于張量算法的高階圖匹配時提出了包含邊和超邊的匹配模型. 文獻[15]從文獻[14]中提出不同階對稱張量組Z-特征值問題, 定義如下.
定義2[15]設Ai∈R[i, n]是實對稱張量,i=2,3, 如果存在λ∈R和非零向量x∈Rn使得
A3x2+A2x=λx,xTx=1
(2)
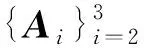
近年來, 文獻[16]提出應用Newton-Gauss-Seidel法可求解不同階張量組方程, 接著文獻[15]提出通過SS-HOPM求解不同階對稱張量組Z-特征值問題(2). 本文接下來介紹應用改進的Newton-法求解問題(2).
1 改進的Newton-法求不同階對稱張量組Z-特征值
首先, 回顧Newton-法求解對稱張量Z-特征值, 從而將該方法推廣到求解不同階對稱張量組Z-特征值. 為了解決對稱張量Z-特征值問題(1), 文獻[17]將對稱張量組Z-特征值問題(1)等價轉化為如下非線性方程組解的問題:
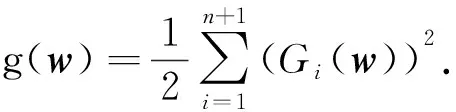
針對問題(2), 將不同階對稱張量組Z-特征值問題等價轉化為如下非線性方程組的解的問題:
(3)
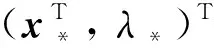
引理1[18]若Ai∈R[i, n]是實對稱張量,i=2,3, 則F(x,λ)的Jacobi矩陣?F(x,λ)為實對稱矩陣, 且具有如下形式:
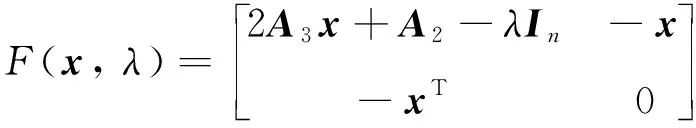
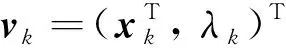
?F(vk)pk=-F(vk)
(4)
為了確保Newton-法的全局收斂性, 根據文獻[17]提出的方法, 引入F(v)的價值函數
顯然, 若F(v*)=0, 則f(v*)=0. 由于f(v)≥0對所有的v恒成立, 因此,f(v)的全局極小值點為F(v)=0的根.
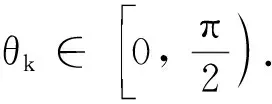
(5)
其中?f(vk)=?FT(vk)F(vk),δ越靠近1, 收斂速度越快. 當pk不滿足(5)式時, 對pk進行修正, 修正式為
(?F(vk)+τk?F-T(vk))pk=-F(vk)
其中?F-T(vk)表示Jacobi矩陣?F(vk)的逆的轉置, 令
Bk=?FT(vk)?F(vk)+τkIn+1
(6)
通過化簡得
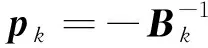
又由文獻[19]中的算法3.3知τk的選取使Bk為正定矩陣且使(5)式成立, 具體過程見算法1.

算法1[19] τk選取的算法輸入: 矩陣Hk=?FT(vk)?F(vk)6: for k=0, 1, …, do輸出: τk+17: ifL·LT=Hk+τkIn+1選取初始點: 給定常數σ8: stop1: ifmin(hii)>09: else2: τ0=010: τk+1=max(2τk, σ)3: else 11: end if4: τ0=-min(hii)+σ12: end for5: end if
選取步長βk滿足如下Wolfe條件
(7)
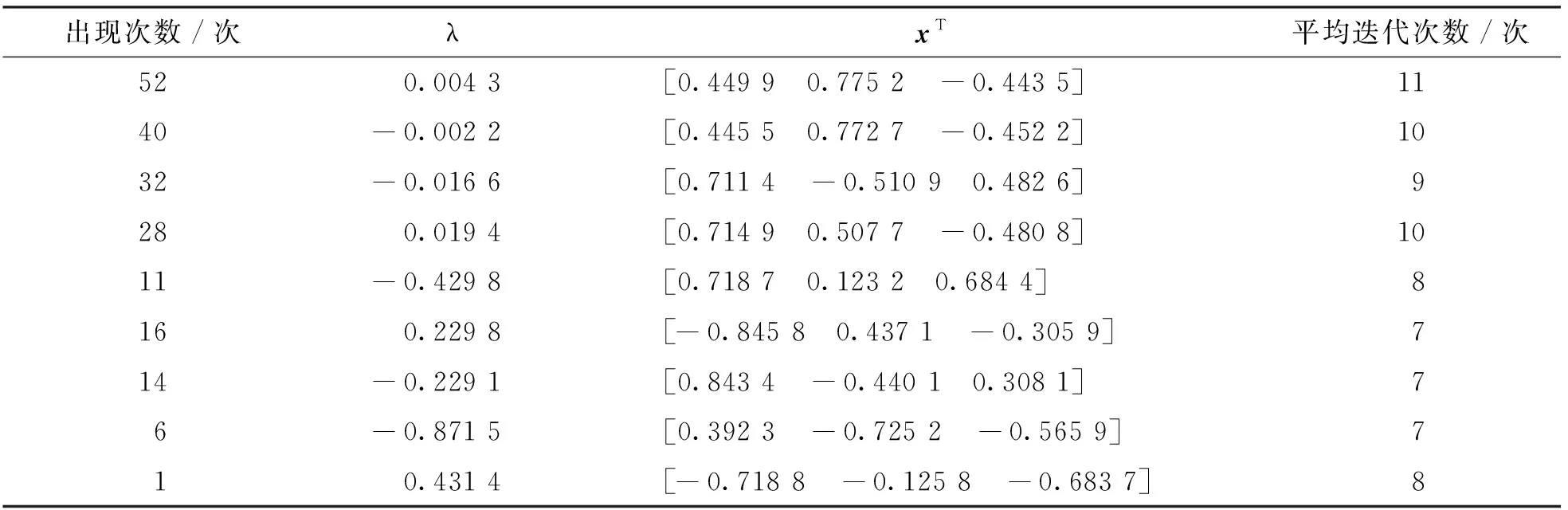
其中: 0 算法2 改進的Newton法求解不同階對稱張量組Z特征值.輸入: 對稱張量{Ai}3i=2∈R[i, n], 初始值x0,λ0,β, 給定常數δ,ε,ρ∈(0, 1), 0 本節分析算法2的收斂性, 首先給出一些假設. 假設1f在Rn+1上有下界, 并且在包含水平集E={v:f(v)≤f(v0)}的開集Ω上連續可微, 其中v0為起始迭代點. 假設2f的梯度?f在Ω上Lipschitz連續. 即存在一個常數L>0, 使得 設d(f)=3, ch(f)=3-4=-1,事實上R3已經考慮到了3-面的所有情況,依次來討論。若f是一個(3,3,3)-面,由引理1(3)和R3.1得若f是一個(3,3,k)-面(k=4,5,6),由引理1.3和R3.2得若f是一個(3,3,7+)-面,由R3.3得ch′(f)≥ch(f)+1=-1+1=0。若f是一個(3,4,4)-面,由引理1(2)和R3.4得 若f是一個(3,4,5+)-面,由R3.5得若f是一個(3,5+,5+)-面,由R3.6得 若f是一個(4+,4+,4+)-面,由R3.7得綜上,3-面得證。 ‖?f(v)-?f(v′)‖≤L‖v-v′‖, ?v,v′∈Ω 引理2[19]如果f滿足假設1和2, 那么考慮vk+1=vk+αkpk這種形式的迭代, 其中pk是下降方向,αk是步長且滿足Wolfe條件(7), 有如下不等式成立 其中θk是pk與-?f(vk)的夾角. 定理1如果函數f(v)滿足假設1和2, 那么由算法2產生的序列{vk}滿足 即改進的Newton-法全局收斂. 定理2若假設1,2,3成立, 且βk=1. 如果?F(v*)是非奇異的, 其中v*是算法2產生的序列{vk}的收斂點, 那么算法2超線性收斂. ‖vk+1-v*‖=ο(‖vk-v*‖) 即{vk}超線性收斂到v*. 本節使用文獻[15]中給出的兩個例子進行數值實驗, 并對二者的結果進行比較. 所有試驗都在MATLAB R2015a中完成, 其配置為: Intel(R) Celeron(R)3205U 1.50 GHz CPU和4.00G RAM內存. 例1設實對稱張量A3=(aijk)∈R[3,3]和實對稱正定矩陣A2=(bij)∈R[2,3], 且元素取值如下: 使用兩種算法進行數值實驗, 在算法2中選取的參數分別是ε=10-7,c1=0.1,c2=0.8, 并用分布在[-2, 2]中的不同隨機初始點x0和λ0進行200次實驗, 最大迭代次數為1 000次, 如果‖?f(vk)‖≤ε, 說明算法收斂. 實驗結果見表1-3. 表1 算法2在例1上的數值結果 表2[15] SS-HOPM算法在例1上的數值結果 表3 兩種算法計算相同特征值所用平均時間 由表1與表2可知, 該數值實驗得出的結果與文獻[15]中的結果相比: 第一, 兩種方法都能求出特征值0.019 4和0.431 4, 但根據表3, 可知算法2計算所用的時間更少一些; 第二, 算法2可以求出14個特征值里的9個, 比文獻[15]中用SS-HOPM所求的特征值多了5個, 其中有7個與文獻[15]求出的特征值不相同. 例2實對稱張量A3=(aijk)∈R[3, 3]和實對稱矩陣A2=(bij)∈R[2, 3], 且元素取值如下: 再次使用兩種算法進行數值實驗, 算法2選取的參數分別是ε=10-7,c1=0.000 1,c2=0.8, 并用分布在[-10, 10]中的不同隨機初始點x0和λ0進行100次實驗, 其最大迭代次數為1 000次, 如果‖?f(vk)‖≤ε, 說明算法收斂, 結果見表4,5. 表4 算法2在例2上的數值結果 表5[15] SS-HOPM算法在例2上的數值結果 對表4和表5的結果比較可知, 算法2要比SS-HOPM所求特征對多, 兩種方法都能算出特征值0.785 9, 但算法2用時為0.085 451 s, SS-HOPM用時為0.144 277 s, 可見算法2用時較少, 且與文獻[15]相比, 得到了新的特征值. 數值例子實驗表明, 改進的Newton-法是一種有效的求解不同階對稱張量組Z-特征值的方法且算法2是全局超線性收斂的. 因此, 改進的Newton-法和SS-HOPM相互補充, 可以求出更多的不同階對稱張量組的Z-特征值.
2 收斂性分析

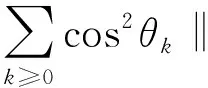
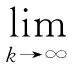
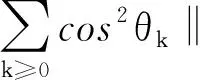
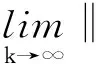
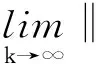
3 數值實驗




4 結論

