Frobenius擴張上的投射余可解Gorenstein平坦模①

高娜娜， 楊剛

蘭州交通大學 數理學院， 蘭州 730070

文獻[1]在研究交換Noether環上的有限生成模的概念時， 引入了G-維數為0的模， 并由此給出了Gorenstein局部環的等價刻畫． 受文獻[1]思想的啟發， 文獻[2]引入了任意環上的Gorenstein投射模、 Gorenstein內射模和Gorenstein平坦模的概念． 之后許多學者對這3類模做了深入研究和推廣． 文獻[3]證明了在任意環R上， Gorenstein投射(Gorenstein內射)模類是投射(內射)可解類， 在凝聚環R上， Gorenstein平坦模類是投射可解類， 并由此進一步研究了Gorenstein投射、 Gorenstein內射和Gorenstein平坦維數． 為了研究所有Gorenstein投射模都是Gorenstein平坦模， 文獻[4]引入了投射余可解Gorenstein平坦模的概念．

環與模的擴張是環與模范疇中的主要研究內容． Frobenius擴張作為一種特殊的環擴張首先由文獻[5]引入． 之后， 文獻[6-7]對Frobenius擴張進行了進一步的研究． 文獻[8]研究了Frobenius擴張上Gorenstein投射模的性質． 受此啟發， 本文主要討論Frobenius擴張上投射余可解Gorenstein平坦模的性質．

本文中R均指有單位元的結合環． 除非特別聲明， 本文中的R-模均指左R-模． P (R)表示投射模類．

1 投射余可解Gorenstein平坦模

定義1[4]如果存在投射R-模的正合列

使得

且對任意內射Rop-模I， 有I?RP正合， 則稱R-模M是投射余可解Gorenstein平坦模．

以下將投射余可解Gorenstein平坦模簡記為PGF模， 以PGF(R)表示投射余可解Gorenstein平坦模類．

引理1[3]如果P (R)?X， 且對任意短正合列

其中X″∈X， 則X′∈X當且僅當X∈X， 稱X是投射可解類．

引理2[1，4]投射余可解Gorenstein平坦模類關于直和、 直和項、 擴張封閉． 投射余可解Gorenstein平坦模類是投射可解類．

命題1若M是投射余可解Gorenstein平坦模， 則存在正合列

其中P是投射R-模，G是投射余可解Gorenstein平坦模．

證由投射余可解Gorenstein平坦模的定義可得．

定義2[9]如果下列等價條件之一成立：

(a) 函子A?R-和HomR(A， -)是自然等價的；

(b) 函子- ?RA和HomRop(A， -)是自然等價的；

(c)RA是有限生成投射模， 并且AAR?(RAA)*=HomR(RAA，R)；

(d)AR是有限生成投射模， 并且RAA?(AAR)*=HomRop(AAR，R)；

則稱環擴張R?A是Frobenius擴張．

以下關于Frobenius擴張的例子參見文獻[9]．

例1(i)對有限群G， Z?ZG是Frobenius擴張；

(ii) 設H是群G的子群， 并且H在G中具有有限的指標n， 其左陪集代表系為g1=e，g2，…，gn，Z是整數環，A=Z[G]是整群代數，R=Z[H]是A=Z[G]的子代數， 則R?A是Frobenius擴張．

引理3[10]設環擴張R?A是Frobenius擴張，M是A-模． 則：

(i) 若M是投射A-模， 則M是投射R-模；

(ii) 若M是內射A-模， 則M是內射R-模；

(iii) 若M是投射R-模， 則A?RM是投射A-模．

對于投射余可解Gorenstein平坦模， 我們有如下結論：

命題2設環擴張R?A是Frobenius擴張，M是A-模． 若M是PGFA-模， 則M是PGFR-模．

證設M是PGFA-模． 則存在投射A-模的正合列

使得

且對任意內射Rop-模I， 有I?RP正合． 注意到Pi是投射A-模， 則Pi是投射R-模， 故P也是投射R-模的正合列．

令I是內射Rop-模． 則I?RA?HomRop(A，I)是內射右A-模， 故有HomRop(A，I) ?AP正合． 由

I?RP?(I?RA)?AP?HomRop(A，I)?AP

有I?RP正合． 因此，M是PGFR-模．

命題3設環擴張R?A是Frobenius擴張，M是R-模． 則M是PGFR-模當且僅當A?RM(HomR(A，M))是PGFA-模．

證充分性 設A?RM是PGFA-模． 由命題2知A?RM是PGFR-模． 注意到RM是A?RM的直和項， 因此M是PGFR-模．

必要性 若M是PGFR-模， 則存在投射R-模的正合列

使得

且對任意內射Rop-模I， 有I?RP正合． 因為Pi是投射R-模， 所以A?RPi是投射A-模． 因此，A?RP是投射A-模的正合列， 且

設I是內射右A-模． 則由引理3知，I是內射Rop-模． 又由

I?RP?(I?AA) ?RP?I?A(A?RP)

易得I?A(A?RP)正合． 故A?RM是PGFA-模．

2 投射余可解Gorenstein平坦維數

定義3定義R-模M的投射余可解Gorenstein平坦維數記為PGfdRM，

其中Pi∈PGF(R)}

若不存在正合序列

其中Pi∈PGF(R)， 則記PGfdRM=∞．

引理4令M是R-模， 則以下結論等價：

(i)PGfdRM≤n；

證注意到投射余可解Gorenstein平坦模類是投射可解類， 類似于文獻[3]的命題2.7， 引理4可證．

以下結論類似于文獻[3]的命題2.19：

引理5設R是環， {Mi}i∈I是一簇R-模． 則PGfdR(?i∈IMi)=sup{PGfdRMi：i∈I}．

證由投射余可解Gorenstein平坦模類關于直和封閉， 顯然

PGfdR(?i∈IMi)≤sup{PGfdRMi：i∈I}

要證

PGfdR(?i∈IMi)≥sup{PGfdRMi：i∈I}

只要證： 若Mi是M的直和項， 則

PGfdRMi≤PGfdRM

當PGfdRM=∞時， 結論顯然成立． 設

PGfdRM=n<∞

由歸納假設， 當n=0時， 由PGF(R)關于直和項封閉， 若M是PGFR-模， 則Mi是PGFR-模， 故PGfdRMi= 0． 假設當PGfdRM=n-1時成立， 即

PGfdRMi≤n-1=PGfdRM

下證結論對n成立． 設M=M1?M2， 并且PGfdRM=n， 取M1，M2的投射分解， 有正合列

其中P1，P2是投射模， 做直和

其中P1?P2是投射R-模， 故

PGfdR(K1?K2)=PGfdRM-1=n-1

由假設知

PGfdRKi≤n-1

則

PGfdRMi≤n=PGfdRM

結論得證．

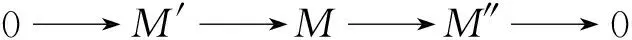
證設

分別是M′和M″的投射分解． 由馬掌引理有以下行和列正合的交換圖：

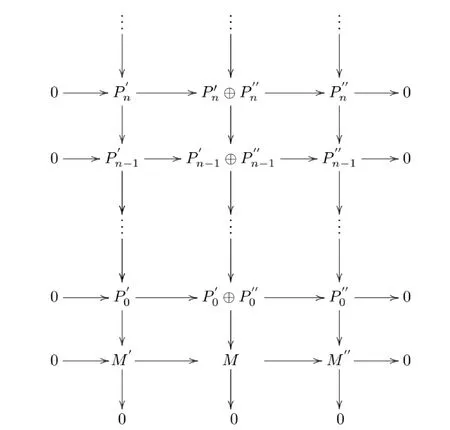
如果記

那么由以上交換圖可得序列

正合， 其中

若PGfdRM″<∞，PGfdRM<∞． 不妨設PGfdRM″≤m， 且PGfdRM≤m． 則由引理4知，Km和K″m均是投射余可解Gorenstein平坦模． 從而由正合序列

可得K′m是投射余可解Gorenstein平坦模． 由引理4知，PGfdRM′≤m．

若PGfdRM′<∞，PGfdRM″<∞． 不妨設PGfdRM′≤m， 且PGfdRM″≤m． 則由引理4知，K′m和K″m均是投射余可解Gorenstein平坦模． 從而由正合序列

可得Km是投射余可解Gorenstein平坦模． 由引理4知，PGfdRM≤m．

若PGfdRM′<∞，PGfdRM<∞． 不妨設PGfdRM′≤m， 且PGfdRM≤m． 則由引理4知，K′m和Km均是投射余可解Gorenstein平坦模． 從而由正合序列

可得PGfdRKm≤1． 由引理4知，PGfdRM≤m+1．

綜上所述， 命題4得證．

命題5設環擴張R?A是Frobenius擴張，M是R-模． 則PGfdR(A?RM)=PGfdA(A?RM)=PGfdRM．

證由命題2， 有

PGfdR(A?RM)≤PGfdA(A?RM)

由命題3， 有

PGfdA(A?RM)≤PGfdRM

故

PGfdR(A?RM)≤PGfdA(A?RM)≤PGfdRM

因為RM是A?RM的直和項， 故由引理5得

PGfdRM≤PGfdR(A?RM)

即PGfdRM=PGfdR(A?RM)， 從而有

PGfdR(A?RM)=PGfdA(A?RM)=PGfdRM

定義4[8]如果滿足：

(a) 環擴張R?A是Frobenius擴張；

則稱環擴張R?A是可分Frobenius擴張．

以下關于可分Frobenius擴張的例子參見文獻[8-9]：

例2(i) 令F是域，A=M4(F)． 設R是A的子代數， 其F-基由下列冪等元和矩陣的單位元構成：e1=e11+e44，e2=e22+e33，e21，e31，e41，e42，e43， 則R?A是可分Frobenius擴張；

(ii) 對有限群G， Z?ZG是可分Frobenius擴張．

定理1設環擴張R?A是可分Frobenius擴張，M是A-模． 則M是PGFA-模當且僅當M是PGFR-模．

證必要性 由命題2可得．

充分性M是PGFR-模， 則存在R-模正合列

對任意I是A-模，I也是R-模， 有I?A(A?RP)?I?RP， 故I?A(A?RP)正合， 即A?RM是PGFA-模． 由環擴張R?A是可分擴張， 有AM是A?RM的直和項， 因此M是PGFA-模．

命題6令環擴張R?A是可分Frobenius擴張，M是A-模， 則PGfdAM=PGfdRM．

證由命題2， 若M是PGFA-模， 則M是PGFR-模， 故PGfdRM≤PGfdAM． 設

PGfdRM=m<∞

則存在R-模正合列

其中Gi是PGFR-模． 由命題3知，A?RGi是PGFA-模(i=1，2，…，m)， 則存在正合列

那么PGfdA(A?RM)≤m． 由環擴張R?A是可分擴張知AM是A?RM的直和項， 故由引理5知

PGfdAM≤PGfdA(A?RM)≤PGfdRM

結論得證．

推論1設環擴張R?A是可分Frobenius擴張，M是A-模， 那么M是PGFA-模當且僅當A?RM(HomR(A，M))是PGFA-模．

證由命題3和定理1可得．

定義5定義R的左整體PGF維數記為lPGFD(R)，

lPGFD(R)=sup{PGfdRX：X是任意左R-模}

命題7設環擴張R?A是可分Frobenius擴張． 則lPGFD(R)=lPGFD(A)．

證對于任意左R-模M， 由命題5知

PGfdA(A?RM)=PGfdRM

因此有

lPGFD(R)≤lPGFD(A)

下證lPGFD(R)≥lPGFD(A)． 任意A-模N， 由命題6知PGfdAN=PGfdRN． 故有

lPGFD(R)≥lPGFD(A)

綜合可得

lPGFD(R)=lPGFD(A)