基于恒等映射多層極限學習機的高速列車踏面磨耗預測模型1)

王美琪 王藝 陳恩利 劉永強 劉鵬飛

(石家莊鐵道大學省部共建交通工程結構力學行為與系統安全國家重點實驗室,石家莊 050043)

(石家莊鐵道大學機械工程學院,石家莊 050043)

引言

自2008 年以來高速鐵路在我國迅猛發展,截止到2019 年末,我國高速鐵路營業總里程突破3.5 萬公里,在線高速動車組3665 標準組,高速鐵路運營里程及高速動車組保有量均占世界2/3 以上,穩居世界第一[1].高速列車的發展極大縮短了乘客的出行時間,但是隨著車輛運行速度的提高,鋼軌的日漸老化,導致了輪軌幾何關系的惡化,從而使車輪踏面磨耗愈發嚴重.這不僅極大增高了高速鐵路的運營成本,而且嚴重影響列車乘坐的舒適性與安全性,列車脫軌等重大事故的發生還會造成國民經濟的重大損失[2-3].因此,對車輪磨耗進行趨勢預測研究,對高速鐵路發展中安全評估與壽命預測有重要的參考意義.

針對上述問題,國內外的專家學者也進行了大量的研究論證.Archard[4]最早提出了接觸物體的材料、相對滑動距離影響物體磨耗的磨耗模型.以Archard 磨耗理論為基礎,一些國外學者從摩擦學角度[5-6]對車輪踏面磨耗進行了研究,并提出了適用于車輪滾動接觸和滑動接觸的磨耗機理.文獻[7]認為車輪磨耗速率與接觸斑面積內能量耗散呈線性關系并以此提出一種車輪磨耗預測模型.文獻[8-9]采用結合了輪軌非赫茲滾動接觸模型和材料摩擦磨耗模型的車輪磨耗計算模型,并通過車輛多體動力學模型研究了車輛系統參數、軌道系統參數和運營條件對車輪型面磨耗演化規律的影響以及高速列車不同運行里程情況下車輪型面的磨耗分布情況.孫麗霞等[10]采用非線性穩定性及蛇行失穩極限環分析方法,研究了車輪磨耗對車輛蛇行運動穩定性的影響規律.由于輪軌接觸融合了車輛動力學、材料學等眾多學科,并且輪軌處于一個開放的系統還受到許多不確定因素的影響.上述方法對于輪軌磨耗的研究僅建立在動力學或摩擦學基礎上,并且無法使用單一的力學模型對各種復雜工況下的輪軌磨耗進行評估及預測.

近年來隨著人工神經網絡的發展,基于數據驅動的網絡訓練與預測在處理非線性問題上具有顯著優勢[11-17].人工神經網絡不僅能夠實現多維空間的壓縮映射,而且能夠實現低維空間的稀疏映射,還能夠實現數據的等維映射.姜涵文等[18]通過TensorFlow架構建立了鋼軌的通過總重預測模型.程澤華[19]通過BP 神經網絡算法構建了接觸線磨耗量預測模型.Zhang 等[20]使用LM (Levenberg Marquard)數值優化算法對BP 網絡進行優化提出一種自適應差分進化LMBP 輪對尺寸預測模型,對CRH380 BL 型車的輪對尺寸進行了預測.Wang 等[21]通過反向傳播神經網絡(back propagation neural network,BPNN)對CRH380 BL 的車輪磨耗進行預測及驗證.

由此可以看出,人工神經網絡憑借其高度的非線性映射能力,被廣泛地應用于鐵路建設的各個方面,但是隨著技術的不斷進步,也對網絡的性能提出了更高的要求.Huang 等[22]在單隱層前饋神經網絡的基礎上提出了極限學習機(extreme learning machine,ELM).相對于傳統的神經網絡,ELM 不僅有較快的學習和訓練速度,而且有較高的訓練精度,目前已經應用在一些相關領域[23-25].文獻[26]結合了PINN (physics informed neural networks)與ELM提出一種PIELM (physics informed extreme learning machine)模型,用于求解復雜幾何中的平穩和時變偏微分方程.Kasun 等[27]提出一種使用ELM-AE(extreme learning machine-auto encoder)初始化隱含層權值的分層無監督訓練多層極限學習機模型.文獻[28]采用外源性輸入神經網絡建立了輪軌磨損預測的非線性回歸模型(nonlinear auto regressive models with eXogenous inputs neural network,NARXNN),用于不同條件下的輪軌磨耗預測.

由此可見,現階段對于高速列車車輪踏面磨耗預測的研究大多是采用傳統的車輛動力學理論,基于數據驅動的高速列車車輪踏面磨耗研究相對較少,在現有的基于神經網絡的車輪踏面磨耗預測研究中,選用的網絡模型如:多層BP 網絡、多層感知器等,均在訓練完成后再通過反向傳播算法對參數進行微調.這類模型大多泛化能力差,訓練速度慢,需進一步開展高速列車車輪踏面磨耗預測的神經網絡算法研究.

本文首先在多層極限學習機中引入恒等映射,提出一種基于恒等映射的多層極限學習機模型(IML-ELM),并通過多特征回歸數據集驗證該模型的網絡性能.然后根據高速鐵路實際列車參數,建立高速動車組列車的多體動力學模型進行磨耗計算,通過搭建的神經網絡模型對車輪踏面磨耗值進行學習和預測,從而驗證本文所提出網絡模型能較好地反映不同參數對車輪踏面磨耗值的影響規律.最后,利用I-ML-ELM 模型對實際列車的踏面磨耗數據進行學習及預測,進一步驗證I-ML-ELM 模型的有效性和適用性.本文采用I-ML-ELM 對高速列車車輪踏面磨耗預測模型進行了研究,以期為高速鐵路發展中安全評估提供參考.

1 恒等映射多層極限學習機基本原理(IML-ELM)

1.1 極限學習機

假設有N組訓練數據 { (qi,ui)|i=1,2,···,N},L,m和n分別為隱含層、輸出層和輸入層的神經元個數,g(·) 為隱含層神經元的激活函數,ELM 的數學模型為

式中,H為ELM 隱含層的輸出矩陣,U為ELM 的期望輸出,β 為ELM 的輸出權值.

當輸入權值 ωj和隱含層閾值b隨機確定后,整個ELM 網絡可以看作一個線性系統,網絡的訓練過程相當于求解方程U=Hβ 的最小二乘解 β,輸出權值為

式中,H+為H的Moore-Penrose (M-P)廣義逆矩陣.

1.2 極限學習機-自動編碼器(ELM-AE)

自動編碼器[29]是一種輸入、輸出神經元個數相等的無監督人工神經網絡,主要用于重構輸入信號.ELM-AE 是Kasun 等[27]于2013 年提出的一種基于極限學習機改進的自動編碼器網絡,其網絡結構如圖1 所示.

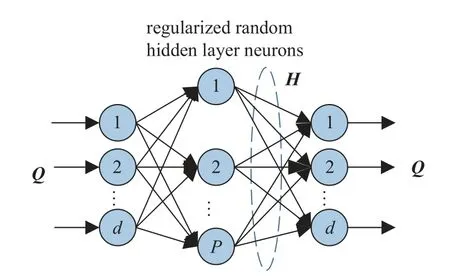
圖1 ELM-AE 網絡結構圖Fig.1 Network structure diagram of ELM-AE

它的主要目的是用三種不同的表示形式有意義地重構輸入特征:

(1) 特征壓縮,代表特征從高維特征空間映射到低維特征空間;

(2) 特征稀疏,代表特征從低維輸入空間映射到高維特征空間;

(3) 特征等維,代表輸入空間與特征空間維度相等.

1.3 恒等映射多層極限學習機基本原理(I-ML-ELM)

本文在多層極限學習機基礎上對網絡結構做出如下改進:在輸出神經元與輸入神經元之間引入恒等映射,使輸出神經元不僅能通過最后一個隱含層的節點獲取數據的重新編碼,而且可以通過恒等映射從輸入神經元直接獲取數據信息,增加了網絡輸出神經元獲取數據的豐富性和全面性,從而達到提高網絡泛化性與準確性的目的.

恒等映射多層極限學習機的結構如圖2 所示,數學模型為

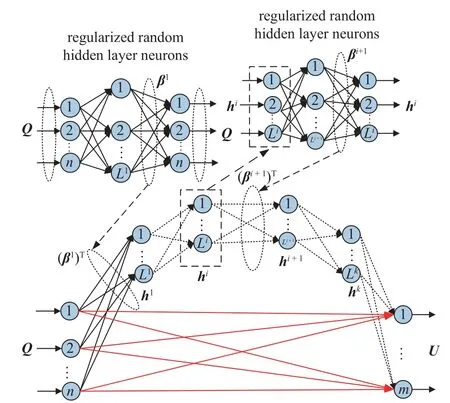
圖2 I-ML-ELM 網絡結構圖Fig.2 Network structure diagram of I-ML-ELM

通過ELM-AE 的訓練將I-ML-ELM 隱含層的權值與閾值確定后,整個網絡的訓練過程可以看作一個線性系統,那么輸出權值W就可以通過最小二乘法的形式解析確定,即

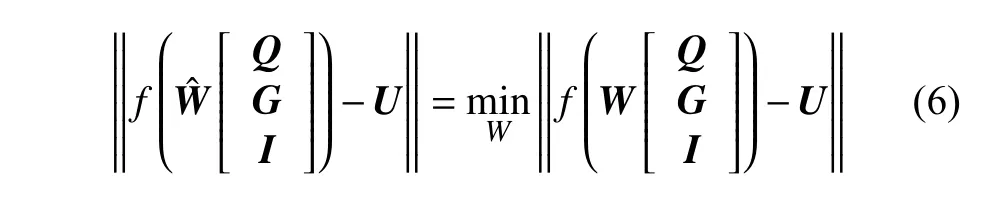
根據Moore-Penrose (M-P)廣義逆矩陣算法,式(6)的解為

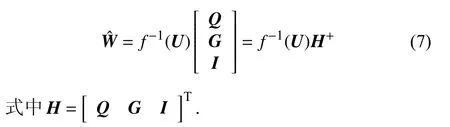
本文建立的恒等映射多層極限學習機模型設定為兩個隱含層,學習算法步驟如下:

Step1:隨機初始化ELM-AE 的輸入權值 ω 和隱含層神經元閾值b;

Step2:使用輸入數據對ELM-AE 進行學習與訓練得出ELM-AE 的輸出權值,存放于I-ML-ELM 的權值棧中;

Step3:將Step2 所得的權重與閾值作為恒等映射多層極限學習機輸入層與第一個隱含層的連接權值 β1;

Step4:將I-ML-ELM 第一個隱含層的輸出矩陣h1,作為ELM-AE 的訓練數據,對ELM-AE 進行訓練,獲得輸出權值,存放于I-ML-ELM 的權值棧;

Step5:將Step4 獲得ELM-AE 的輸出權值 β2作為I-ML-ELM 第二個隱含層與第一個隱含層之間的連接權值;

Step6:I-ML-ELM 的隱含層權重已經初始化完畢,通過最小二乘法求取I-ML-ELM 的輸出權值.

2 實驗與分析

恒等映射的引入使得輸出層神經元可以直接從輸入層神經元獲取數據信息,網絡的數據來源更豐富,有利于提高模型的泛化性能,以及數據預測的準確性.

為了驗證本文提出的預測模型的準確性與泛化性,本文選取machine CPU,wine quality,California housing 和estate valuation 四個多維回歸數據集作為樣本數據集,上述數據集均來自開源數據庫UCI(University of California Irvine) 機器學習數據庫,每個數據集70%的數據用作訓練數據,其余作為測試數據,四個數據集的基本信息如表1 所示.

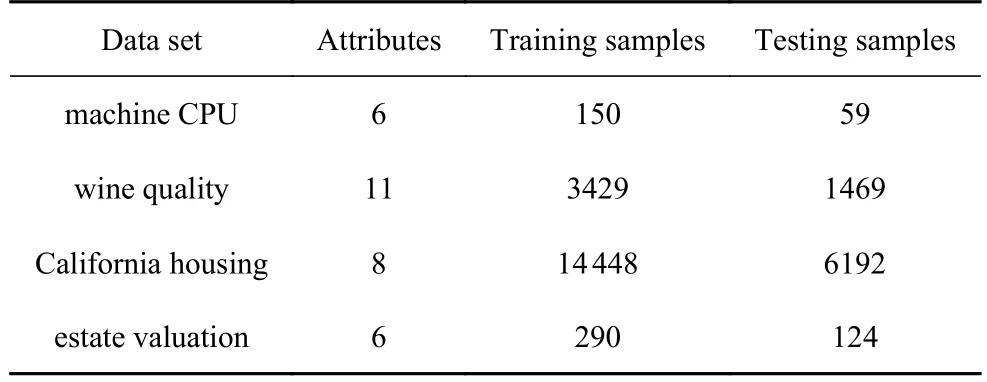
表1 數據集的基本數據信息Table 1 Basic data information of data set

本文選取五種網絡:ELM,FLN,DLSFLN,MLELM,ML-KELM,與本文提出的I-ML-ELM 網絡模型進行對比.其中ELM,FLN,DLSFLN,ML-ELM 中的激活函數均為Sigmoid 函數,ML-KELM 網絡中的內核函數類型為RBF 型.ML-ELM,ML-KELM 網絡的隱含層數量與I-ML-ELM 一致.

本文對兩隱含層神經元個數進行單一變量分析,采用控制變量法對兩隱含層神經元個數進行分析,其結果經可視化處理后如圖3 所示.將網絡輸出的均方根誤差值RMSE 作為網絡精度的表征值,RMSE 值的計算如式(8)所示,數據經可視化處理,可視化處理如式(9)所示

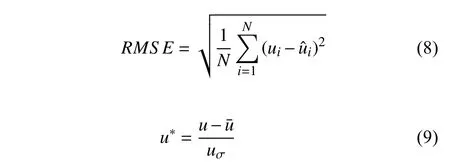
式中,為原始數據的均值,uσ為原始數據的標準差.

在N1ON2平 面以上為數值大于數據均值,在N1ON2平面以下為小于數據均值.RMSE值越小表明網絡的精度越高,本文以1 為步長,兩層神經元個數由1 增加到30,N1,N2分別為第一個隱含層、第二個隱含層神經元個數.由圖3 可以看出,第一個隱含層神經元個數不變時,隨著第二個隱含層神經元個數增多,網絡的精度逐漸提高,但是隨著神經元個數的持續增長,網絡精度不再提高.第二個隱含層神經元個數不變時,隨著第一個隱含層神經元個數的增多,網絡的精度出現一定程度的波動后不再變化.所以本文選定第一個隱含層神經元個數為1,第二個隱含層神經元個數為7.

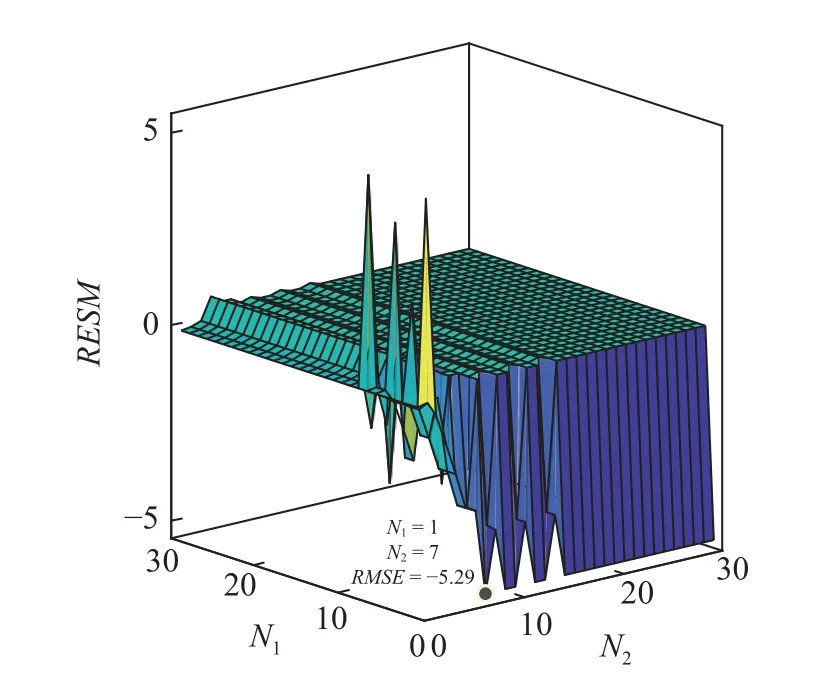
圖3 不同隱層神經元條件下的網絡回歸精度變化趨勢Fig.3 Variation trend of network regression accuracy under different hidden layer neurons

為了進一步分析模型預測效果及準確度,選取以下四種經典的網絡性能評價指標作為預測效果評判標準:均方根誤差RMSE、最大絕對誤差MAXE、平均絕對誤差MAE、平均絕對百分誤差MAPE.上述四種值越小表示測試輸出越接近測試數據的期望輸出.指標的計算公式如式(8)、式(10)～式(12)所示

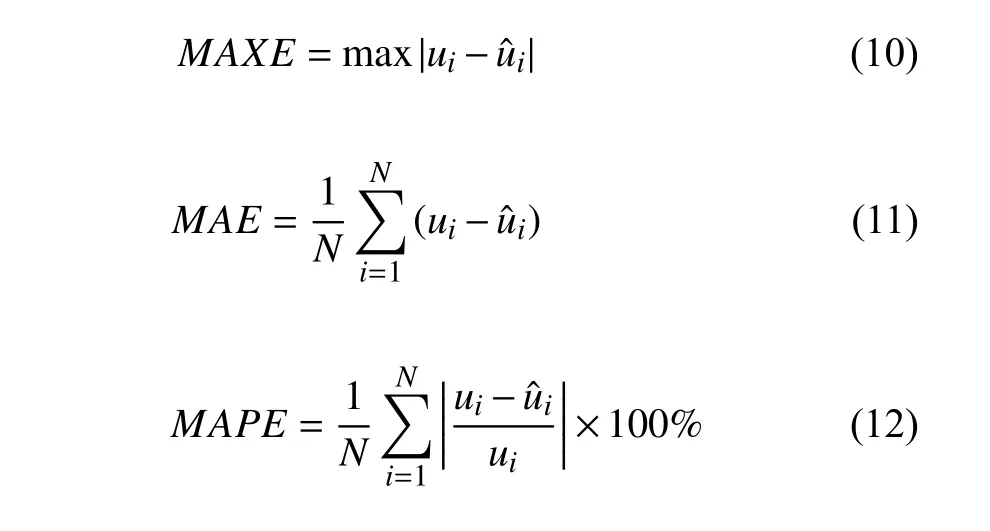
RMSE值代表模型的回歸精度,數值越小,說明該方法的預測準確度越高.由表2 可以看出,I-MLELM 算法在不同數據集下的RMSE值分別為0.0322,0.0015,0.1399,0.0012,小于其他五種算法在同一數據集下的RMSE值.在estate valuation 數據集下ELM,FLN 的RMSE略小于I-ML-ELM 算法的RMSE值,但是ELM,FLN 在其他數據集下的RMSE值,并沒有表現出比I-ML-ELM 算法更好的效果.所以從總體的RMSE值來看,本文提出的I-ML-ELM 算法在表中所示的網絡中回歸精度更高并且在四種數據集下的綜合效果最好,在不同數據集下的適用性也更高.

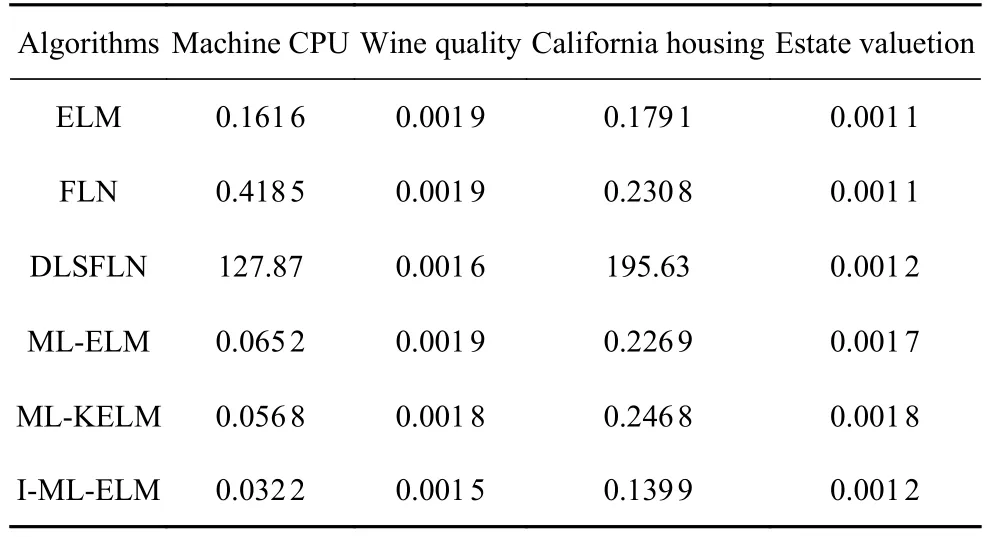
表2 算法在不同網絡下數據集RMSE 值比較Table 2 Obtained RMSE by different networks of the algorithm

MAXE,MAE和MAPE多用于反映預測誤差的實際情況.

如表3 所示,I-ML-ELM 算法在不同數據集下的MAXE值分別為0.1284,0.0072,1.2638,0.0048,該值小于其他幾種算法在同種數據集下的MAXE值.

由表3 可以看出ML-KELM 在某一數據集中的MAXE值略小于I-ML-ELM 的MAXE值,但是ML-KELM 在其他數據集,以及表4 表5 所示的評價指標中性能表現并不優越.所以整體來看I-ML-ELM 算法在四種數據集下的預測誤差依然優于其他算法.

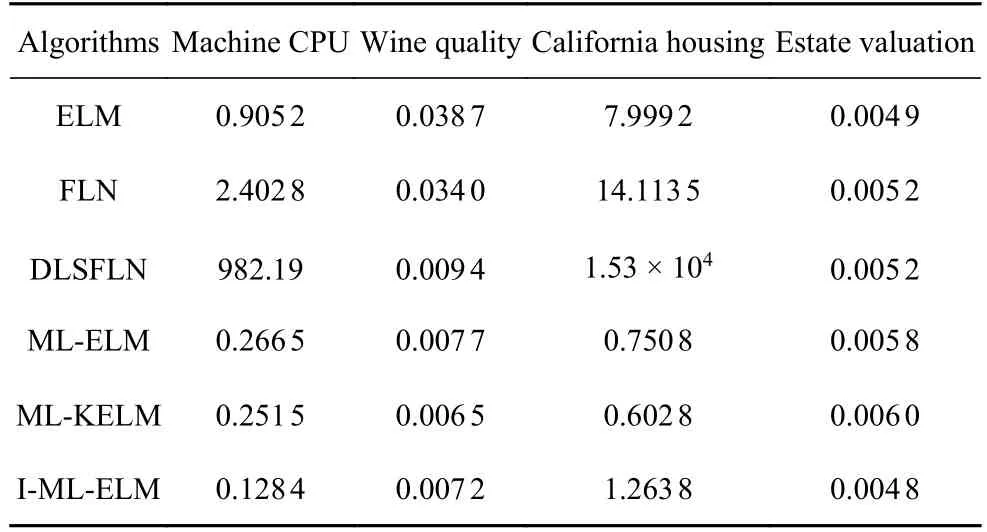
表3 算法在不同網絡下數據集MAXE 值比較Table 3 Obtained MAXE by different networks of the algorithm

表4 算法在不同網絡下數據集MAPE 值比較Table 4 Obtained MAPE by different networks of the algorithm

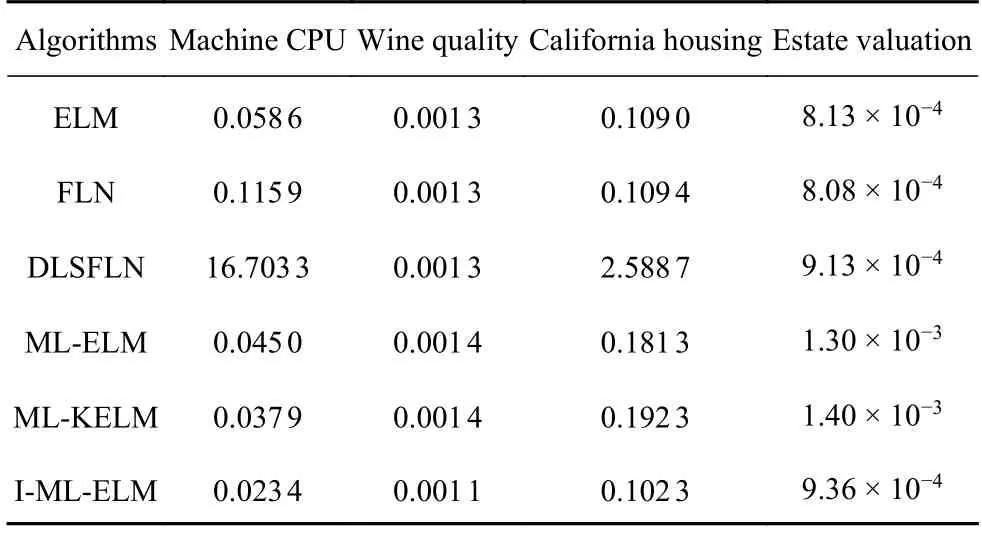
表5 算法在不同網絡下數據集MAE 值比較Table 5 Obtained MAE by different networks of the algorithm

縱觀RMSE,MAXE,MAE,MAPE四種性能指標,本文所提出的I-ML-ELM 算法在各項指標中的綜合性能優于其余五種算法,網絡的回歸精度更高,泛化性能更好.

表6 給出了幾種不同算法在同一數據集下的網絡預測耗時對比,本實驗均在處理器AMD R52600、主頻3.4 GHz、內存16 GB、Windows1064 位操作系統、軟件Matlab 2020a 環境下進行,由于在網絡訓練過程中隱含層權值與閾值為隨機給定,故表6 中數據均由網絡運行30 次,取30 次測試時間的平均值進行對比.

由表2 至表5 的對比結果,可以看出本文提出的I-ML-ELM 網絡具有較高的準確性和較好的泛化性能,結合表6 可以看出,該網絡同時也具備了較高的計算效率.在estate valuation 數據集下的表現略差于ML-KELM,但綜合四種數據集及其他幾種性能指標來,看I-ML-ELM 算法的網絡綜合性能依然優于其他算法.

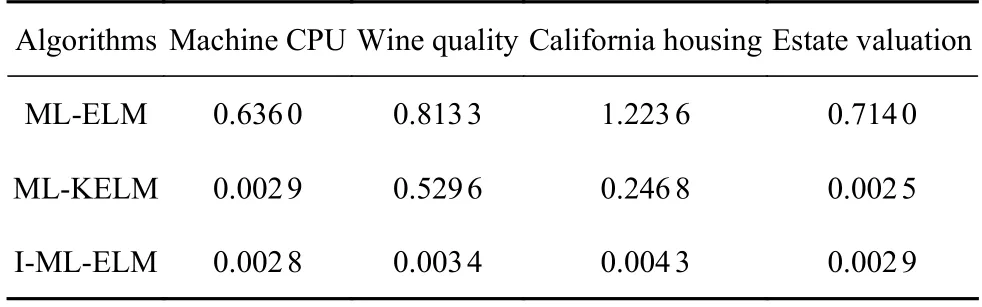
表6 算法在不同網絡下數據集的測試時間(s)比較Table 6 Data test time (s) comparison of the algorithm under different networks

3 車輪磨耗預測實驗分析

3.1 車輛-軌道耦合動力學模型建立

根據車輛-軌道耦合動力學理論及高速列車的實際參數,如表7 所示,建立了單節車廂的車輛-軌道耦合動力學模型.

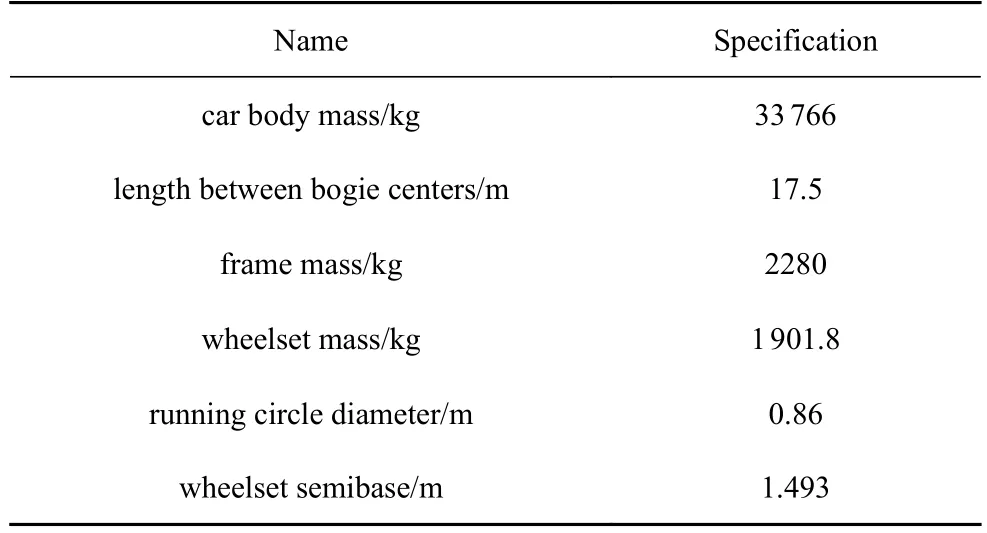
表7 高速列車主要參數Table 7 Basic parameters of high-speed vehicle

車體模型主要由1 個車體、2 個構架、4 個輪對等部件組成,其中車體、構架、輪對均包含橫向、垂向、縱向、側滾、點頭、搖頭6 個自由度,軸箱為1 個自由度,整車共計50 個自由度.

車體和轉向架之間通過二系懸掛進行連接,二系懸掛包括空氣彈簧、二系橫向減振器及抗蛇行減振器.轉向架和輪對之間通過一系懸掛進行組合,一系懸掛裝置包括一系垂向減振器、轉臂軸箱和一系鋼彈簧.

軌道采用移動質量軌道模型,在定義了軌道垂向和橫向的總體剛度和阻尼后,增加了鋼軌模型.并且軌道始終跟隨車輪,具有等效質量和轉動慣量,鋼軌地面之間采用彈簧阻尼相連.

3.2 車輪踏面磨耗模型

Archard 模型[4]中磨耗體積與法向力、滑動距離成正比,與材料硬度成反比,即

其中,Wv是磨耗體積,FN是法向力,s是滑動距離,Hw為材料硬度.k是無量綱磨耗系數,取值與接觸應力和滑動速度有關,其關系如圖4 所示(該磨耗圖[30]根據摩擦實驗建立).

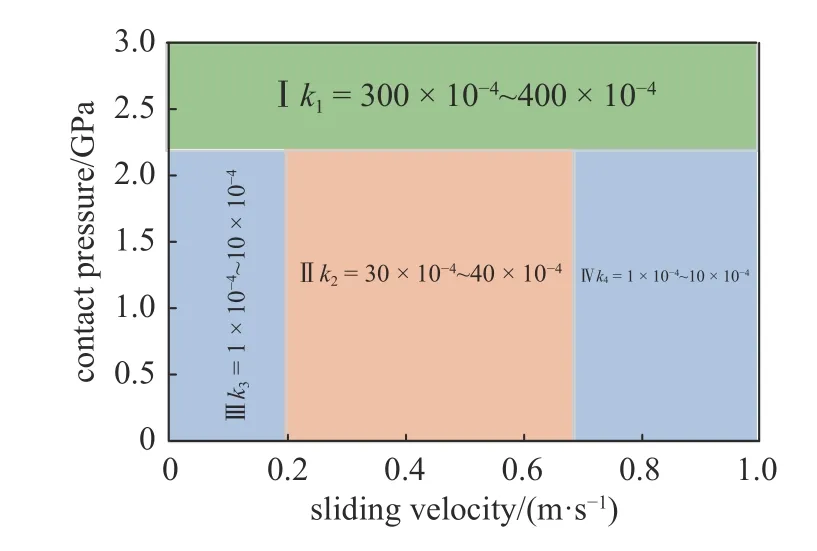
圖4 磨耗系數分布圖Fig.4 Wear coefficient map

本文采用UM 中基于摩擦功的Archard 磨耗模型,該模型認為磨耗體積與摩擦功呈線性關系為

其中,P是摩擦功率,即

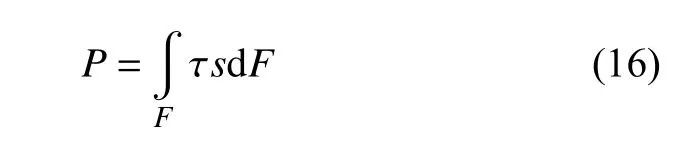
式中,τ 是接觸單元內的切向應力,s是滑動速度,F是接觸斑面積.

3.3 輪軌滾動接觸力學模型

當高速列車運行在復雜工況時,輪軌的接觸關系不符合Hertz 接觸理論,故本文采用基于虛擬滲透法的輪軌非橢圓多點接觸算法(K-P 算法)[31]計算輪軌法向力.

對于輪軌接觸的法向接觸應力pz(x,y) 計算方式為

式 中,δ0為 滲透 量;k(y)=zwheel(y)?zrail(y) 代 表x=0平面上車輪型面曲線zwheel(y) 與鋼軌型面曲線zrail(y)兩點間的距離.

輪軌接觸斑面積近似服從下式

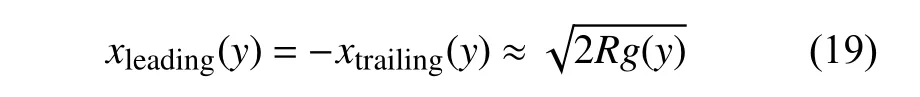
由此可通過積分運算得到輪軌接觸法向力

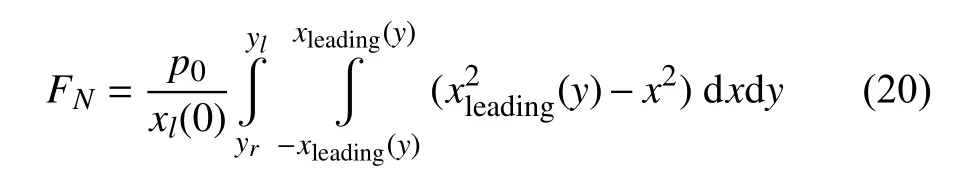
式中,yl表示在y方向的接觸斑邊界.

點(0,0)處的法向變形位移為

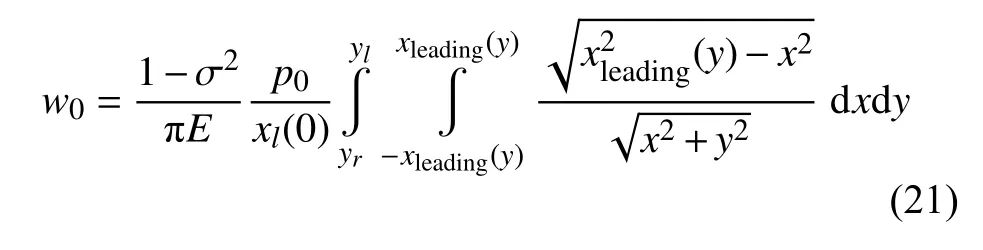
式中,σ 為泊松比,E為楊氏模量.(0,0)處的滲透值為 δ0=2w0(0,0)=2w0,可得輪軌接觸法向力

采用針對非橢圓接觸面修正的FASTSIM 算法計算切向力.將接觸斑等效成橢圓接觸斑,需滿足以下兩個條件:

(1) 等效橢圓的長短軸之比與K-P 模型得到的接觸斑長寬之比相等;

(2) 等效橢圓的面積與K-P 模型計算得到的接觸斑面積相等.

那么接觸區域中切向應力的分布為

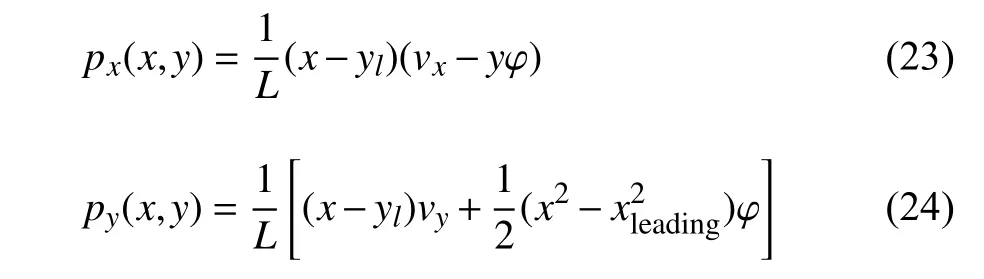
式中,vx,vy和 φ 分別為縱向、橫向和自旋蠕滑率,在接觸斑內對式(23)和式(24)進行積分即可求得接觸力.

3.4 仿真分析

在車輪磨耗仿真中,假設車輪踏面形狀在更新前始終保持不變,每次迭代計算以車輛運行里程值作為車輪踏面更新的判斷依據.迭代次數為磨耗模擬的重復次數.磨耗迭代是對相同結構的一系列計算,只是在初始踏面廓形上有所不同,一次迭代是對一組配置的單個計算.里程是分配給一個磨耗步驟的里程,在每一個磨耗步驟結束時,里程值用來衡量磨耗深度.磨耗步數為一次迭代中踏面廓形更新的次數,步數越多且里程越少,則踏面廓形演進越接近實際,但是建模時間也越長.因此本實驗中磨耗步數設為2000,里程設為5 km.

基于建立的高速列車車輛-軌道耦合動力學模型,通過多體動力學軟件采用控制變量法對不同運行速度、運行里程及不同曲線半徑的線路進行磨耗仿真計算,得到相應的踏面磨耗值,并對數據進行對比分析.最后通過恒等映射多層極限學習機數據預測模型,對踏面的磨耗深度進行學習和預測.

圖5 為列車在曲線半徑為8000 m 的線路中以300 km/h 速度運行,獲取到不同運行里程下轉向架左前輪的車輪磨耗變化趨勢及磨耗深度.通過圖5可以看出,車輛運行10000 km 時踏面磨耗深度約為0.12 mm.隨著運行里程的增加,車輛運行到50000 km時,車輪踏面的磨耗范圍變大,踏面磨耗深度在0.5 mm 左右.當運行到155000 km 時,踏面磨耗深度在1.4 mm 左右.主要的磨耗區間為(?30 mm～30 mm),輪緣部分基本沒有磨耗,車輪磨耗量最大值是0.9 mm 左右,磨耗最深處位于車輪踏面10 mm 附近.由此我們可以看出,車輪踏面磨耗主要位于車輪名義滾動圓附近,并且向兩側延伸.

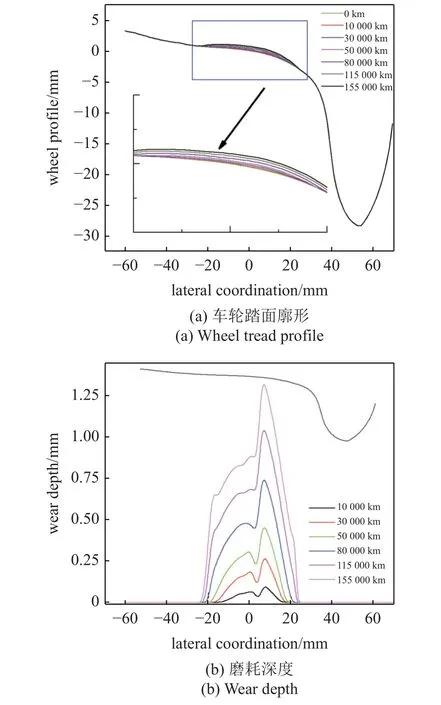
圖5 列車運行不同里程時踏面廓形及磨耗深度Fig.5 The tread profile and wear depth under different mileage of train operation

改變列車的運行速度時,車輪的踏面磨耗值也會發生相應的變化,圖6 為列車在不同運行速度下運行100000 km 時的踏面的磨耗深度及最大磨耗深度.

由圖6(a)可以看出,隨著車速的提高,車輪踏面的最大磨耗深度隨著運行速度的升高呈現升高的趨勢,并且升高量越來越大.列車的運行速度在300 km/h 時,車輪踏面最大磨耗深度為0.9 mm;當列車運行速度達到350 km/h 時,車輪最大磨耗深度為0.923 mm;當列車運行速度達到380 km/h 時,車輪踏面的最大磨耗深度到達了0.98 mm.由圖6(b)可以看出,列車在不同運行速度下,對磨耗的主要區域也有影響.當車輛運行速度為250 km/h 時,踏面磨耗深度約0.88 mm,隨著車輛運行速度的提高,主要磨耗區間出現微小延展但基本沒有變化,但是當速度達到380 km/h 時,磨耗區域有明顯延展,向左側延伸約1 mm,向右側延伸約5 mm.

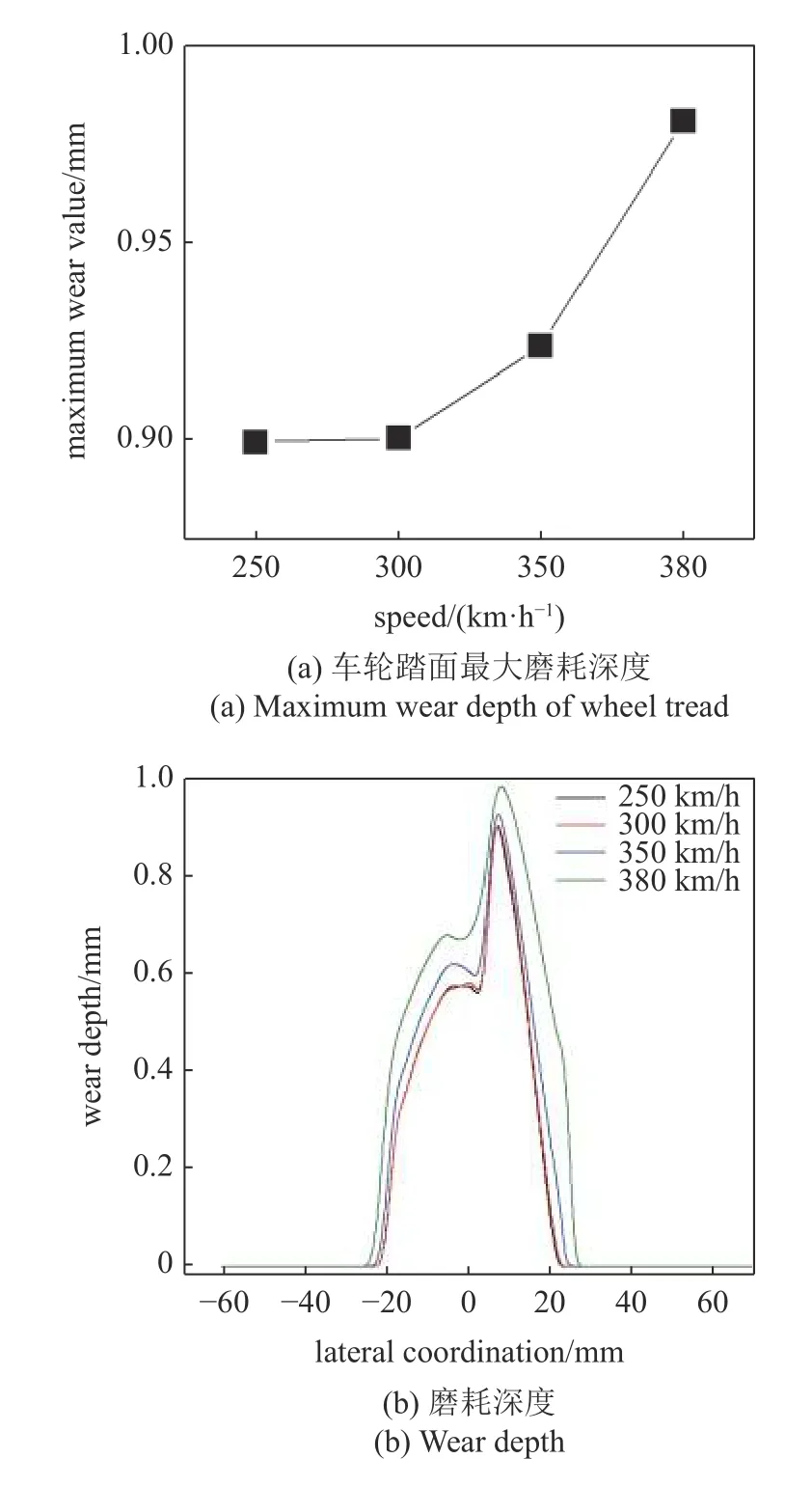
圖6 不同車速下列車運行100000 km 磨耗深度Fig.6 100000 km wear depth of train running at different speeds

對于線路條件的設定本文采用單一線路條件的設定,其中曲線部分曲線半徑的取值通過機車車輛動力學性能評定及試驗鑒定規范選擇.由仿真結果可以看出,當列車通過不同曲線半徑的線路時,對車輪踏面磨耗的影響也是不同的.

由圖7 可以看出,車輪踏面的最大磨耗值隨著曲線半徑的增大呈現出先減小后平穩的趨勢.7000 m 的曲線半徑值作為轉折點,當列車通過線路的曲線半徑小于7000 m 時,隨著曲線半徑的增大,踏面的最大磨耗值呈現大幅減小,當列車通過線路的曲線半徑大于7000 m 時,踏面的最大磨耗深度值趨于平穩.

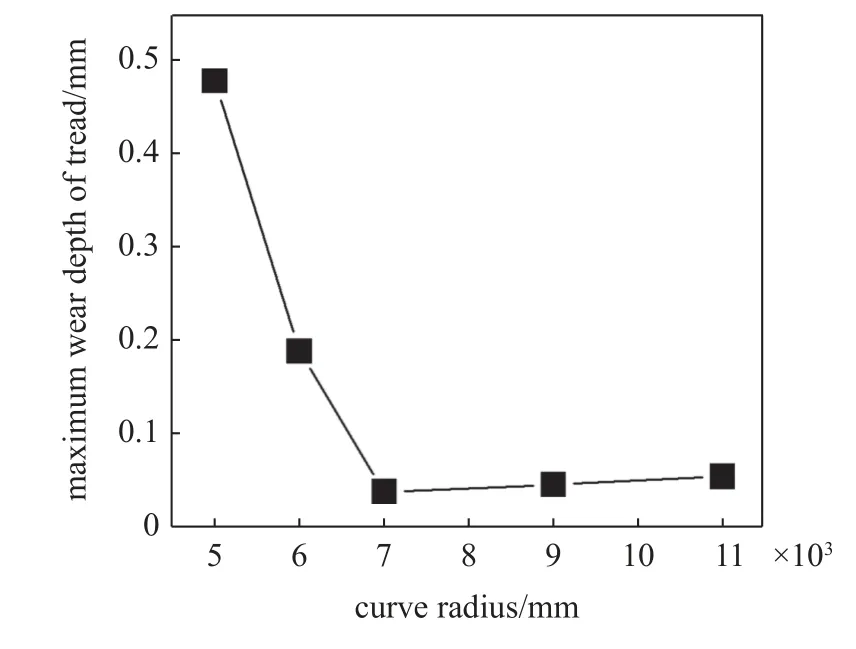
圖7 不同曲線半徑下車輪磨耗深度值Fig.7 Wheel wear depth under different curve radius

通過以上的數據分析及對比,可以看出,在不同的速度、運行里程和曲線半徑的情況下,車輪的踏面磨耗會有相應的變化.因此本文選擇行車速度、運行里程和線路曲線半徑作為神經網絡的輸入變量.通過在UM 中獲取到的315 組數據作為數據集,其中221 組作為訓練數據集,剩余94 組作為測試數據集,使用不同的算法對車輪的磨耗深度值進行預測.其結果如表8 所示.

由表8 可以看出,本文所提出的I-ML-ELM 模型的RMSE,MAXE,MAPE,MAE值遠小于其他算法,也就是說I-ML-ELM 預測模型,在車輪踏面磨耗預測方面表現出比其他五種算法更好的網絡性能.由此可以看出,I-ML-ELM 模型能準確地建立列車不同的運行參數與車輪磨耗之間的映射關系,通過改變列車的運行參數,可以得到不同的踏面磨耗值,可有效用于車輪踏面磨耗的預測.

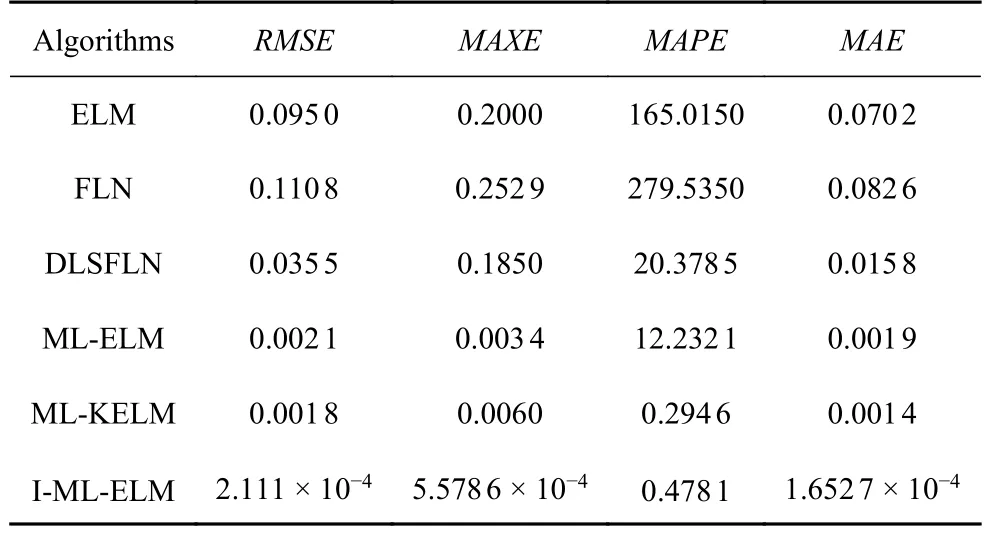
表8 不同網絡模型在仿真數據下的性能參數Table 8 Performance parameters of different network models under simulation data

3.5 實測數據分析

通過鐵路現場對該型高速列車一節車廂進行跟蹤和測量獲取的車輪踏面數據如圖8 所示.由圖像可以看出,踏面的主要磨耗區域為(?20 mm～20 mm),隨著列車運行里程的增大,磨耗程度不斷加深,其中鏇后車輪到運行80000 km 時磨耗增長速率較快,運行80000 km 到115000 km 時增長較平緩.鏇修后的車輪,運行到115000 km 其磨耗增長約0.45 mm.

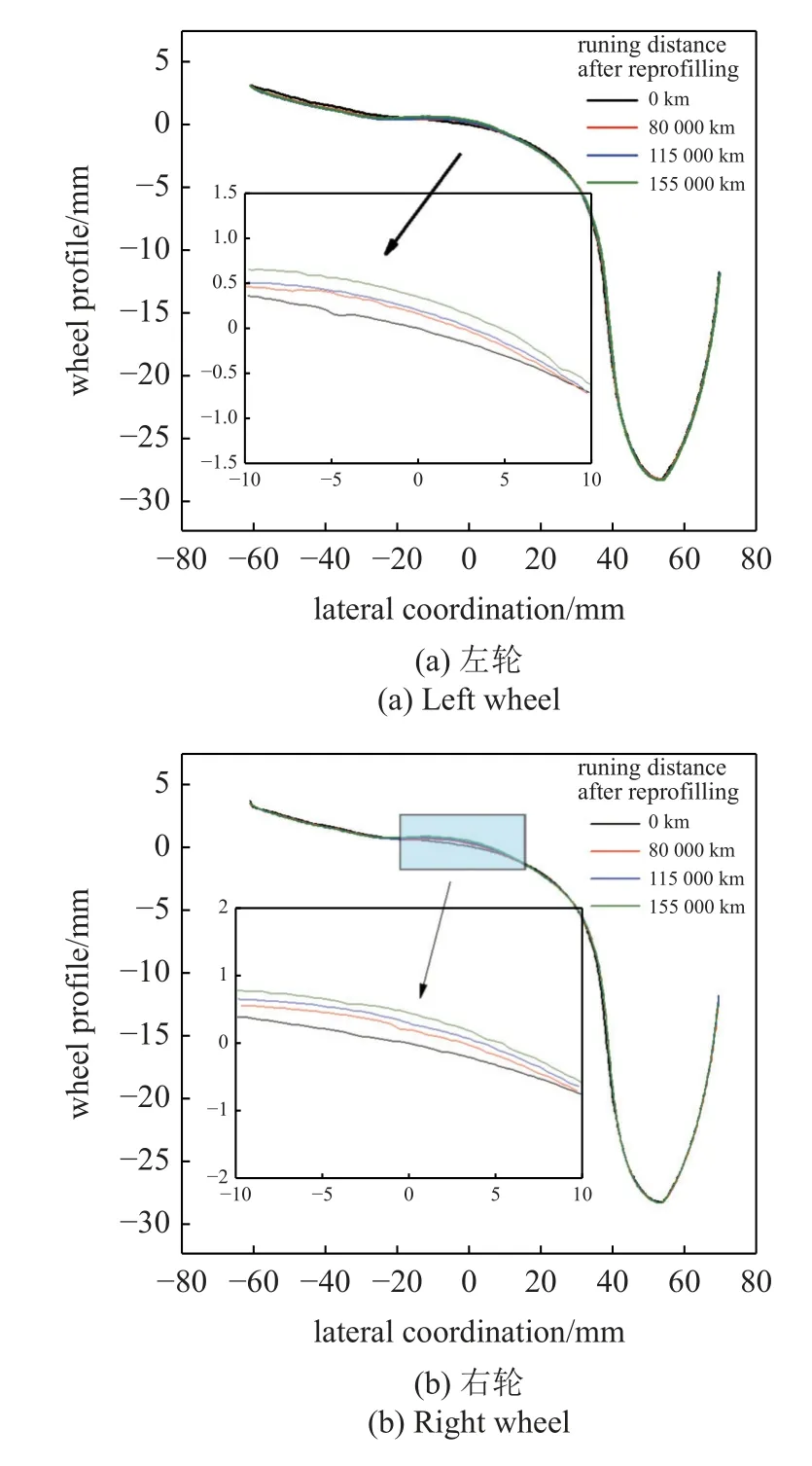
圖8 實測列車運行不同里程下車輪踏面廓形圖Fig.8 Measured wheel tread profile under different mileage of train operation

為了進一步驗證I-ML-ELM 模型的預測精度和有效性,將列車運行里程作為輸入變量,車輪踏面名義滾動圓處的磨耗深度作為輸出,使用本文提出的I-ML-ELM 預測模型進行訓練及預測,結果如圖9及表9 所示.通過對比實際測量值和神經網絡預測值,從而驗證I-ML-ELM 模型預測的準確性.通過表9 可以看出,本文所提出的I-ML-ELM 神經網絡模型的RMSE,MAXE,MAPE,MAE值均小于其他網絡,說明本文提出的預測模型在踏面磨耗預測方面優于其他網絡模型.

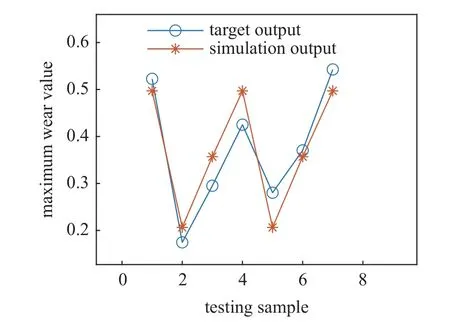
圖9 測試樣本的踏面磨耗預測值和實際測量值對比圖Fig.9 Comparison between predicted value and sample value of testing sample of wheel tread wear value

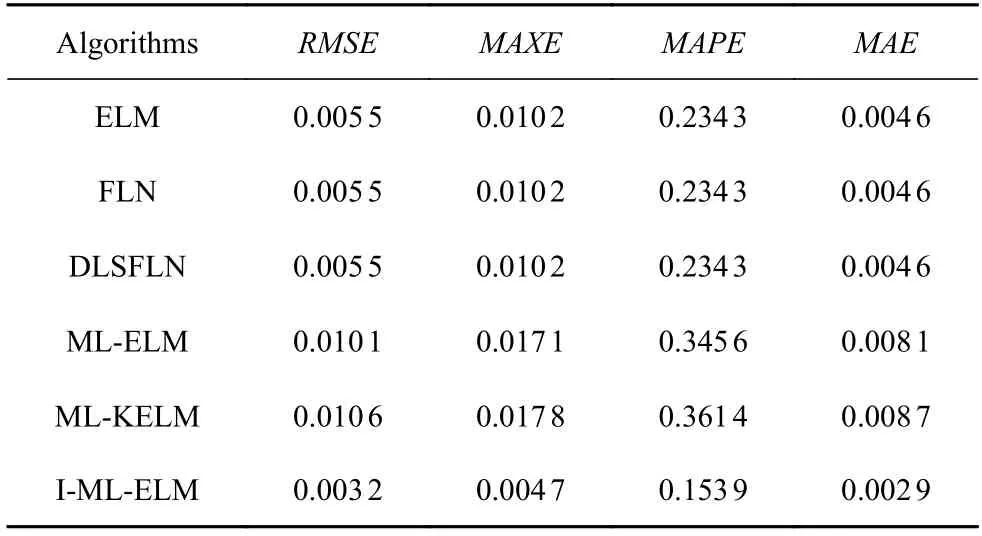
表9 不同模型在現場數據下的性能參數Table 9 Performance parameters of different algorithms under field data

4 結論

在多層極限學習機中引入恒等映射,提出一種恒等映射多層極限學習機模型,建立了基于恒等映射多層極限學習機的高速列車車輪踏面磨耗預測模型.通過I-ML-ELM 磨耗預測模型對高速列車車輪踏面磨耗量進行了學習及預測,以期為車輪的安全評估提供參考.本文的主要結論如下.

(1) 提出恒等映射多層極限學習機算法,并通過不同類型、不同數據量的公共數據集進行了性能測試,驗證了I-ML-ELM 模型具有較高的預測精度與較好的泛化性.

(2) 提出了一種基于恒等映射多層極限學習機模型的車輪踏面磨耗預測方法,通過I-ML-ELM 模型對不同工況條件下的磨耗值進行學習和預測,驗證了該模型的有效性.

(3) 對不同工況下高速列車模型最大磨耗深度值的預測結果表明,本文所搭建的恒等映射多層極限學習機模型的性能參數指標均優于ELM,FLN,DLFLN,ML-ELM 和ML-KELM.仿真結果表明相對于其他神經網絡模型,本文中所提出的I-MLELM 預測模型對高速列車踏面磨耗深度值的預測值更接近實際測量值,從而驗證了I-ML-ELM 具有較高的預測精度.