一類面向高階精度自適應流動計算的流場插值方法1)

周 帥 肖周芳 付 琳 汪丁順

* (中國航空發動機研究院,北京 101300)

? (杭州電子科技大學計算機學院,杭州 310018)

引言

隨著計算機軟硬件技術的發展,以計算流體力學(computational fluid dynamics,CFD)為核心的數值模擬技術已成為空氣動力學領域工程與科學問題分析中一項不可或缺的工具[1].然而,針對復雜幾何外形和復雜流動問題,CFD 計算仍然面臨求解精度和效率的挑戰[2].網格自適應技術[2-8]和高階精度數值方法[9-14]的結合有望提升CFD 復雜問題適應能力,還可在更少的網格上獲得更快的漸進收斂速度[2,10].然而,這兩項技術卻并未在主流商業CFD 軟件中使用.這主要是由于網格自適應技術涉及諸多環節的協同工作,其還存在魯棒性問題,并且要將這兩項技術結合還需要解決一系列技術難題[2].其中一個難題便是如何將前一自適應迭代步中的計算結果高精度地插值到后一迭代步的自適應更新網格中,這一個過程稱為物理量插值.

物理量插值又被稱為物理量轉移或物理量重映[15-25],是將物理量從一網格上轉移到另一網格上,其常被應用于網格變形[16-19]和網格自適應更新[15]等計算問題中.在自適應流場計算中,通過物理量插值可使當前流場計算延續上一迭代步中的計算狀態,從而加速流場計算的收斂速度[20-21].該過程中需關注物理量守恒和插值精度等特性.前者將物理量在從背景網格單元轉移到新網格單元上后,需保持物理量的守恒;對于后者,物理量的插值精度應和當前采用的數值方法精度一致.

以上物理量插值的兩個特性對于提升整個自適應流場計算流程的穩定性具有重要的作用[21],尤其在非定常流動計算中,由物理量插值導致的數值誤差會累積到之后的流動計算中.簡單的線性插值算法無法滿足物理量守恒特性,且其只能達到一階插值精度.文獻[15]提出了針對二維非結構網格的滿足物理量守恒及二階精度的物理量插值算法,物理守恒通過局部網格相交運算實現,二階精度通過重構物理量梯度實現.隨后,Alauzet[22]繼續將該物理量插值算法拓展到了三維非結構網格上.文獻[17,23]采用基于ENO 方法實現物理守恒的物理插值方法,文獻[23]在二維網格上實現了三階精度的物理量插值.針對二維四邊形網格物理量插值問題,Lei 等[24]發展了基于WENO 的高精度插值方法.Zhang 等[25]針對高階間斷伽遼金(DG)數值解在變形網格和移動網格應用中的物理量插值需求,設計了DG 插值方法,實現了守恒和高階的物理量插值.

本文提出一類滿足物理量守恒和高精度的物理量插值方法,以適應高階精度自適應流動計算.為實現流場插值過程中物理量守恒,該方法先計算新舊網格的重疊區域,然后將物理量從重疊區域的舊網格轉移到新網格中.為滿足高階精度要求,先采用kexact 最小二乘方法[26]對舊網格上的數值解進行重構，得到滿足精度要求的物理量分布多項式,隨后采用高斯數值積分實現物理量精確地轉移到新網格的各單元上.本文算法有助于推進網格自適應技術和高階精度數值方法的結合,從而提升CFD 復雜問題適應能力.

1 算法流程

考慮二維自適應流動計算,記Mnew為前迭代步網格(也稱為新網格),Mback為上一迭代步中的網格(也稱為背景網格),本文算法目的為將分布在Mback上的物理量插值到Mnew中,使得插值后的解具有(r+1)階精度并滿足在插值過程中物理量守恒.為實現上述目的,本文算法步驟如下.

(1) 物理量重構:針對Mback中的每個網格單元,構建描述流場物理量在該單元中分布的r次多項式表達式U(x,y).

(2) 網格相交計算:利用Mback中的網格邊將Mnew中的每個網格單元分割得到多個子單元,這些子單元為Mnew中對應單元與Mback中不同網格單元的重疊部分.

(3) 物理量轉移:針對Mnew中的每個網格單元,根據分布于Mback上的流場物理量U(x,y)累積分布于該單元對應子單元上的物理量,累積結果作為該單元上的物理量總量,并以該單元單位面積上的物理量為其參考點上的物理量值.

上述步驟中,步驟1 和步驟3 是實現高階精度流場物理量插值的關鍵.其中,步驟1 用于將背景網格上的物理量重構為r階精度,步驟3 用于確保物理量轉移到新網格后保持r階精度,將在第2 節和第3 節分別討論這兩部分內容.步驟2 中分割后的子單元用于實現插值過程中物理量守恒,其中涉及網格求交計算較為成熟[27-29],本文不再贅述.特別地,本文對在二維非結構三角形網格間插值進行闡述,其思想同樣適用于三維非結構四面體網格.

2 物理量重構

本文采用應用于有限體積法中的k-exact 最小二乘法[26]進行舊網格上的物理量重構.為了完整性,將結合本文中的流場插值需求,簡述該算法過程.物理量重構的目的為針對背景網格Mback上的任一網格單元i,構建關于該單元參考點的物理量分布r次多項式

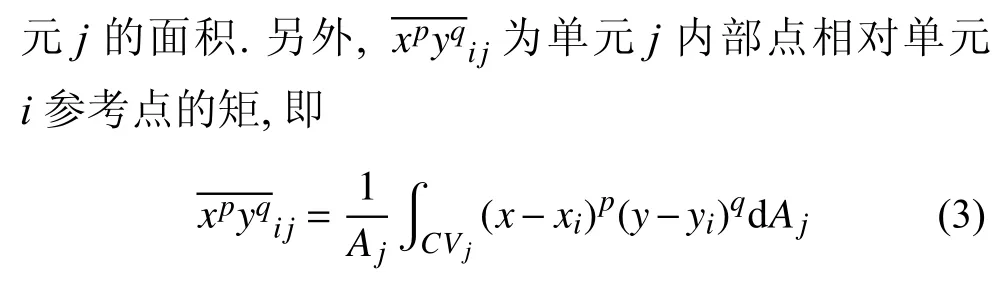
該式的計算僅跟網格幾何位置相關,關于其計算方法請參考文獻[26].

從式(1)和式(2)可知,在二維情形中,次數為r的多項式含有(r+1)(r+2)/2 個未知項系數.為求解這些未知項,需選擇(r+1)(r+2)/2 個單元i的鄰接單元并針對每個單元建立一個如式(2)的等式.在實踐中,通常選擇多于(r+1)(r+2)/2 個鄰接單元構建方程數多于未知項數的方程組[24],這些鄰接單元被稱為單元i的重構模板.隨后,采用最小二乘法求解這些未知項,即式(1)中的多項式系數.

3 流場插值

3.1 滿足物理量守恒的插值

在自適應流動計算中,不同迭代步的網格通常相互獨立.不失一般性,本文考慮相互獨立的網格間的物理量插值情形.如圖1(a)所示,黑色邊表示的網格為Mback,紅邊表示的網格為Mnew(為便于展示,此處只以部分網格單元示意這兩套網格).圖1(b)展示網格相交計算后獲得Mnew中網格單元△ABC對應的子單元結果,共有4 個子單元,分別為與Mback中三個單元重疊的區域.

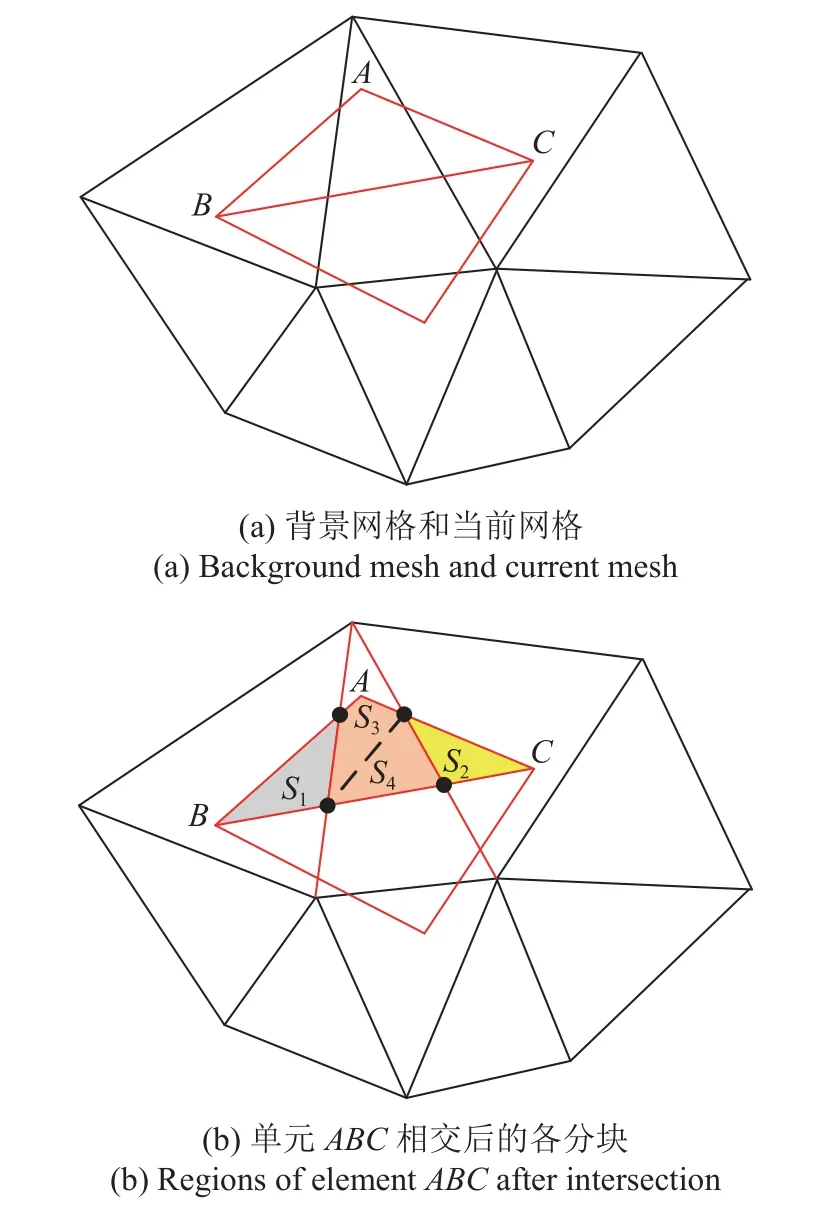
圖1 二維物理量守恒插值示意圖,背景網格和當前網格分別用黑邊和紅邊表示Fig.1 Schematic diagram of two-dimensional conservation of physical quantity interpolation,the background mesh and the current mes are represented by red and black edges respectively

3.2 高階精度插值

從式(4)可知,為求解Mnew中網格單元內的物理量需進行體積分計算,該計算的精度將影響最終的流場插值精度.為獲得高精度積分結果,本文采用高斯積分求解式(4)右端的積分項,即

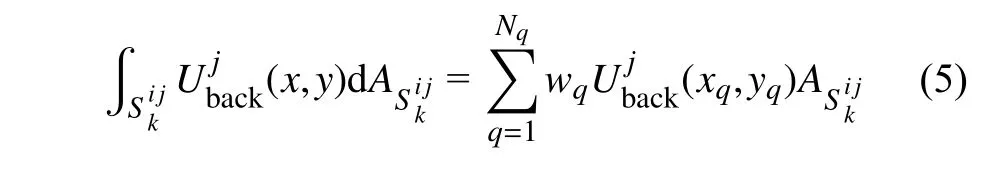
式中,Nq為高斯積分點個數,(xq,yq)為積分點坐標,wq為對應該積分點的權重.注意,高斯數值積分的精度和采用的高斯積分點個數相關.為此,針對不同的精度要求,需采用不同的積分點數及相應的積分點坐標和積分點權重.

為支持高階精度的流場插值,針對積分區域為三角形情形,采用文獻[26,30]中推薦的高斯積分點信息.表1 展示了針對2～ 4 階精度被積函數所采用的高斯積分點數、坐標和相應權重.注意,表1 中所列的積分點坐標為其重心坐標.當所采用的流場數值計算方法精度高于4 階時,需采用更多的高斯積分點數.

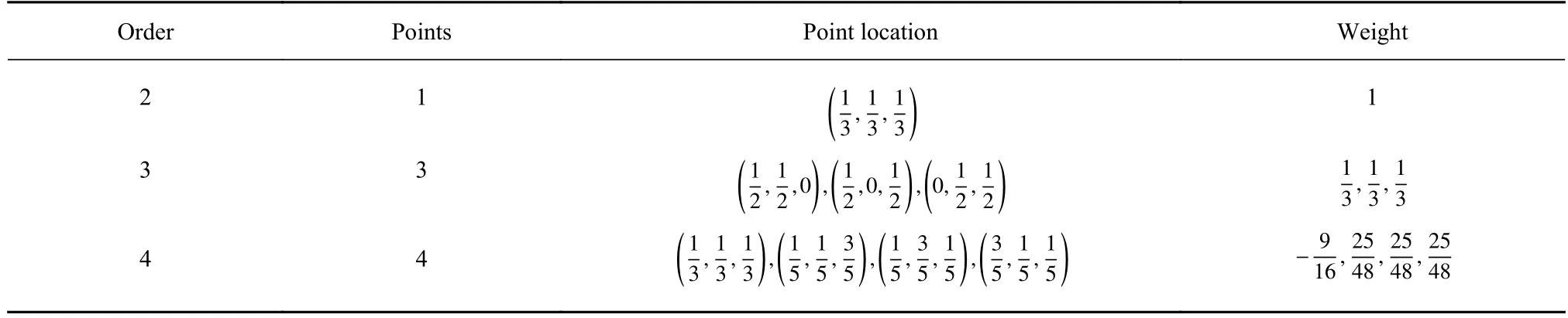
表1 不同階數精度對應的積分點信息Table 1 Information of integration points corresponding to different order

4 數值實驗

選用兩個例子測試本文提出的面向高階自適應流動計算的流場插值方法,第一個例子通過具有解析解的流場驗證該算法的插值誤差,第二個例子則將該算法應用于高階自適應流動計算中.文中所有測試例子均在小型工作站上運行,計算機配置為,內存容量:16 GB;CPU 型號:六核Inter Core i7-8700,主頻:3.2 GHz.

4.1 圓環模型

該模型為四分之一圓環模型[26],圓環內圓半徑為2、外圓半徑為3 (如圖2 和圖3 所示).考慮非黏性超音速渦流流經該模型,流場邊界條件為:內圓邊界為入口邊界,在此處的馬赫數為Mi=2、質量密度ρi=1.區域其他位置的流場變量(密度ρ、速度分量u、速度分量v和壓力P)值由以下式子定義

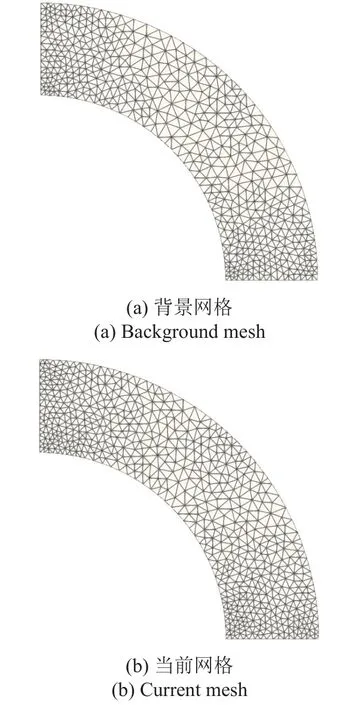
圖2 第一組網格Fig.2 The first group of meshes

圖3 第二組網格Fig.3 The second group of meshes

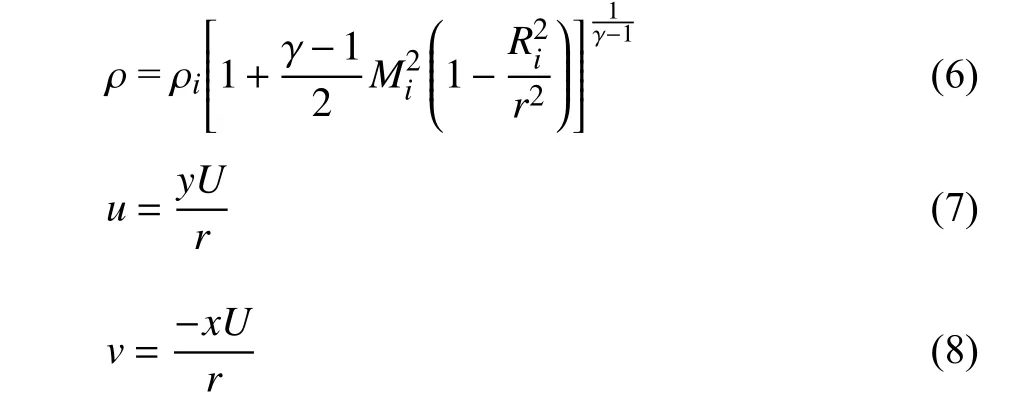
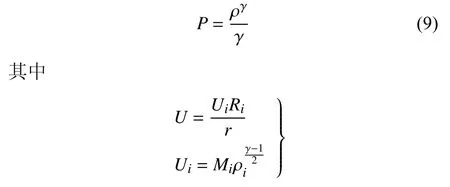
在自適應流場計算中,為延續上一迭代步的計算狀態,需要在每一迭代步開始前執行流場插值過程,以獲得該迭代步的初始解.本文模仿自適應流場計算過程中的插值過程,即將定義在一套網格(背景網格)中的流場插值到另一套網格(當前網格)中,不同的是此處定義在背景網格上的流場通過流場變量的解析式(6)～ 式(9)求出.為驗證本文插值算法的精度,除了從背景網格上獲得的插值解之外,在新網格上也通過流場變量的解析式計算精確解.隨后,針對每一個新網格上的網格單元,根據以下式子計算插值誤差

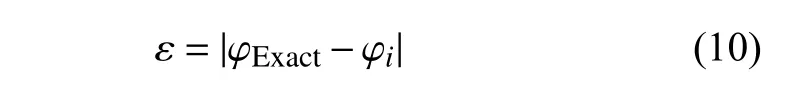
式中,φExact和 φi分別表示在該單元上基于精確值和流場插值得到的單位面積上的物理量值.

為實現上述插值誤差計算,設置兩組不同規模的網格,每組網格由兩套網格組成,分別為背景網格和當前網格,且背景網格的網格單元數比當前網格單元數少.圖2 和圖3 分別展示了這兩組網格,表2顯示了這兩組不同規模網格的網格單元數和網格點數,第二組網格的規模大于第一組網格的規模.表3展示了在不同插值精度情形下在這兩組不同規模的網格上得到的插值誤差的L1范數、L2范數和L∞范數.從表中數據可知,當網格規模相同時,插值精度階數越高,插值誤差越小;當插值精度相同時,網格規模越大,插值誤差越小.

表2 兩組不同規模的網格數據Table 2 Two groups of meshes with different scales

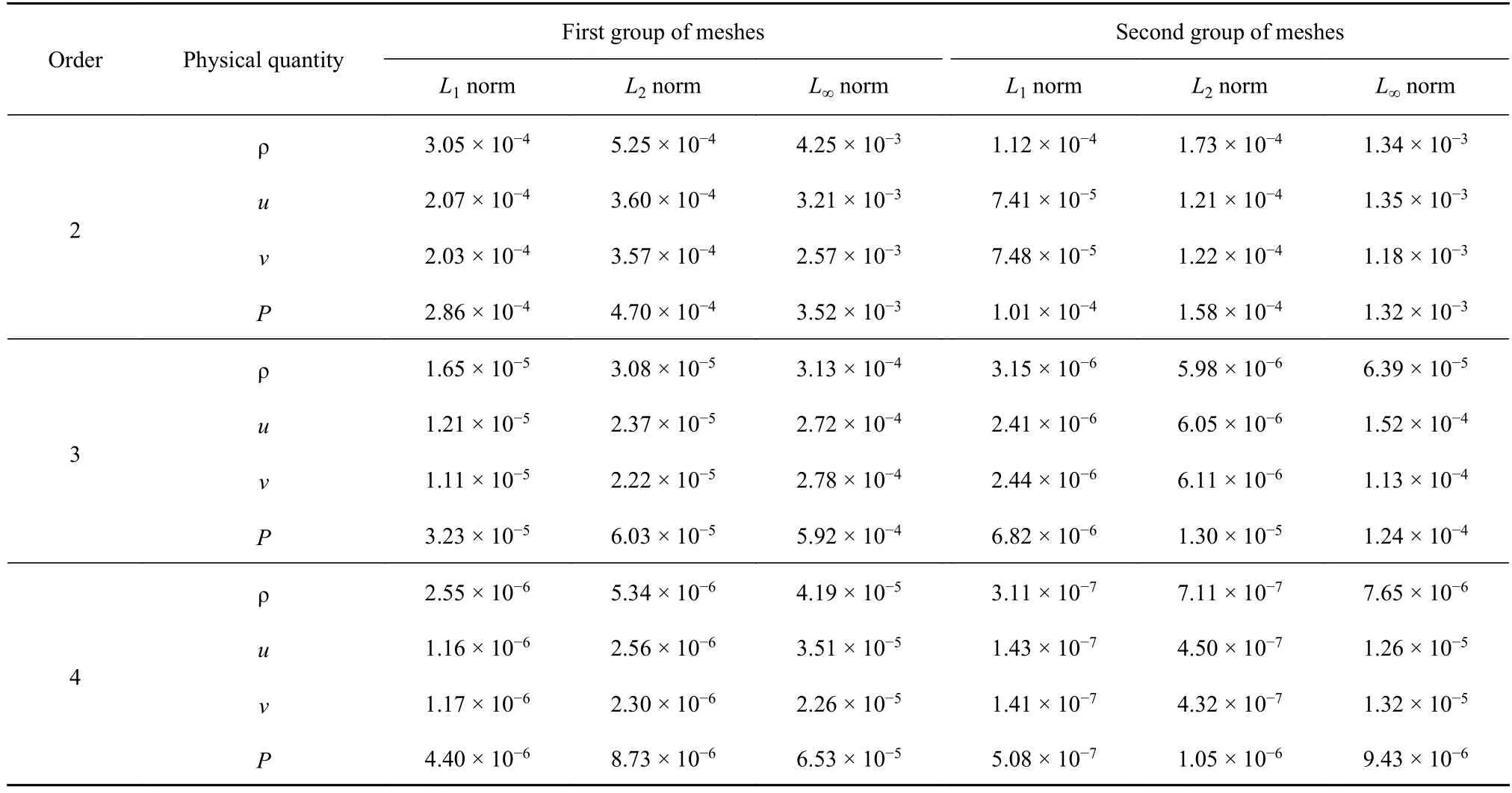
表3 在不同網格規模和不同插值精度下的流場插值誤差Table 3 Interpolation errors of flow field under different mesh scales and different orders of interpolation accuracy

4.2 NACA 0012 模型

以NACA 0012 翼型外流場數值計算為例驗證本文插值方法在自適應流動計算中的有效性.該翼型外流場的計算條件為:雷諾數Re=5000,馬赫數Ma=0.5 和攻角a=0.為獲得該流場數值解,采用3 階精度的高階流場求解器進行自適應迭代求解.圖4(a)中的網格為初始計算網格,由7790 個網格單元和3966 個網格點組成.該初始網格在翼型附近區域分布較稀疏(見網格放大圖),難以捕捉翼型附近區域的精細流場特征.為此,采用自適應技術根據流場解更新計算域網格,并基于新的網格重新計算流場數值解.

本文采用文獻[31-32]中的方法根據流場解計算用于更新網格的單元尺寸場,并采用局部操作技術更新網格.最終,通過6 次自適應迭代獲得收斂的流場數值解.圖4(b)～圖4(d)展示了前四次自適應迭代計算的網格,可以發現隨著自適應迭代次數的增加,翼型附近區域和尾跡區的網格越來越密,因此網格單元數和網格點數也不斷增加(見表3).圖5 展示了自適應計算收斂過程中氣動系數(升力系數和阻力系數)隨網格規模變化的變化.最終,升力系數值收斂于0.000572(理想值為0);阻力系數收斂的值為0.0555,這和文獻[33]中展示的基于多種網格計算得到的阻力系數值接近.圖6 展示了自適應迭代收斂后的馬赫數分布圖,可以發現在翼型附近區域和尾跡區具有清晰的流場特征.

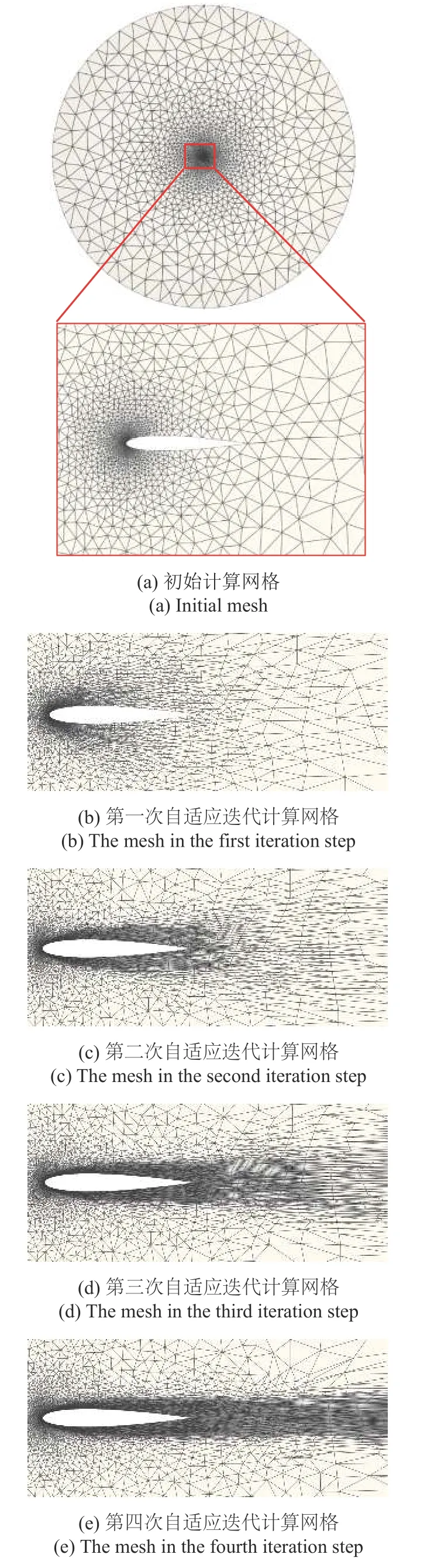
圖4 翼型計算域在不同自適應計算迭代步中的網格Fig.4 Meshes of the airfoil computational domain in different adaptive computation iteration steps

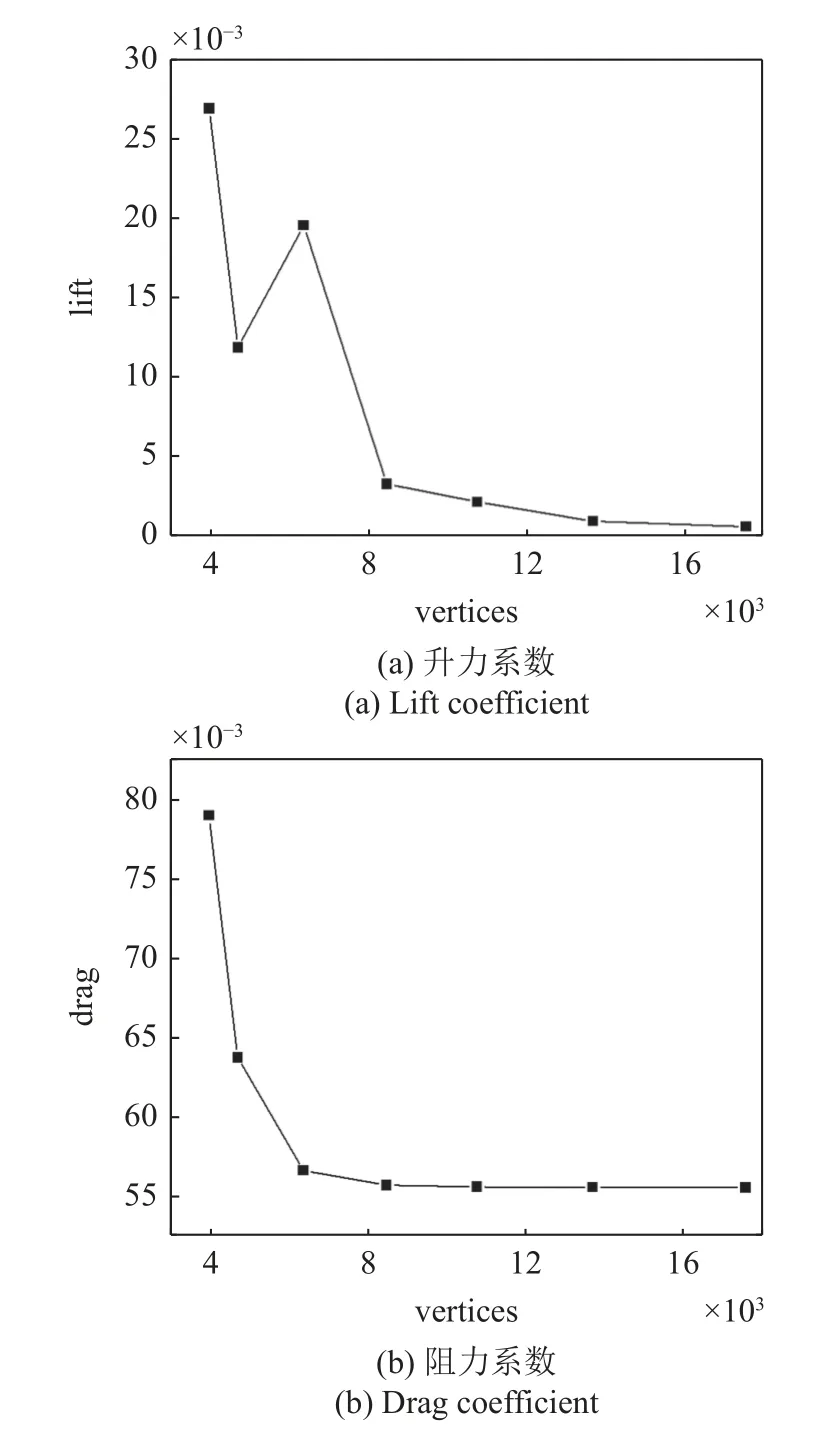
圖5 自適應計算收斂過程中氣動系數隨網格規模變化的變化Fig.5 Convergence of lift and drag coefficients against degrees of freedom (vertices)

圖6 自適應迭代收斂后的馬赫數分布圖Fig.6 The distribution of Mach number after adaptive solution convergences

本文流場插值方法已集成于上述所采用的高階流場求解器中,為說明該插值方法在自適應流場計算中的作用,對比有流場插值功能和無流場插值功能時,求解器在每一自適應迭代步中的求解收斂情況.在每一次自適應計算中,需要在新網格上重新求解流場控制方程,該求解過程最終轉化為線性方程組的迭代求解,求解收斂條件為殘差小于給定門限值(本文中采用的值為1.0 × 10?9).在無流場插值步驟時,每次自適應計算從給定初始值開始進行流場控制方程求解;而在有流場插值步驟時,自適應計算則以上一次計算結果插值到當前網格后的解作為初始計算條件從而延續上一次自適應計算狀態.

表4 展示了在分別有流場插值和無流場插值步驟時,每一次自適應計算收斂迭代步數和收斂時間.因為可以延續上一次計算狀態,流場插值功能可以有效縮短在新網格上的收斂迭代步數,從而縮短收斂時間.如在第一次自適應計算時,無流場插值步驟時,求解器需要15 迭代步來求解流場控制方程;而在有流場插值步驟時求解迭代步縮短到11 步,收斂時間從40.1 s 降到33 s,加速比為1.22.隨著自適應次數的增加,網格規模越來越大,所需的數值求解時間也增多.從表中數據可知,當網格規模越大時,流場插值功能在提高收斂速度方面效果越明顯.如在第6 次自適應迭代計算中,當添加流場插值功能后,收斂迭代步數從29 步降低到10 步,收斂時間從294.6 s 降低到125.3 s,收斂加速比為2.35.需要說明的是,在本算例中,不管是否有流場插值功能,每一次自適應迭代計算都收斂到相同的結果.

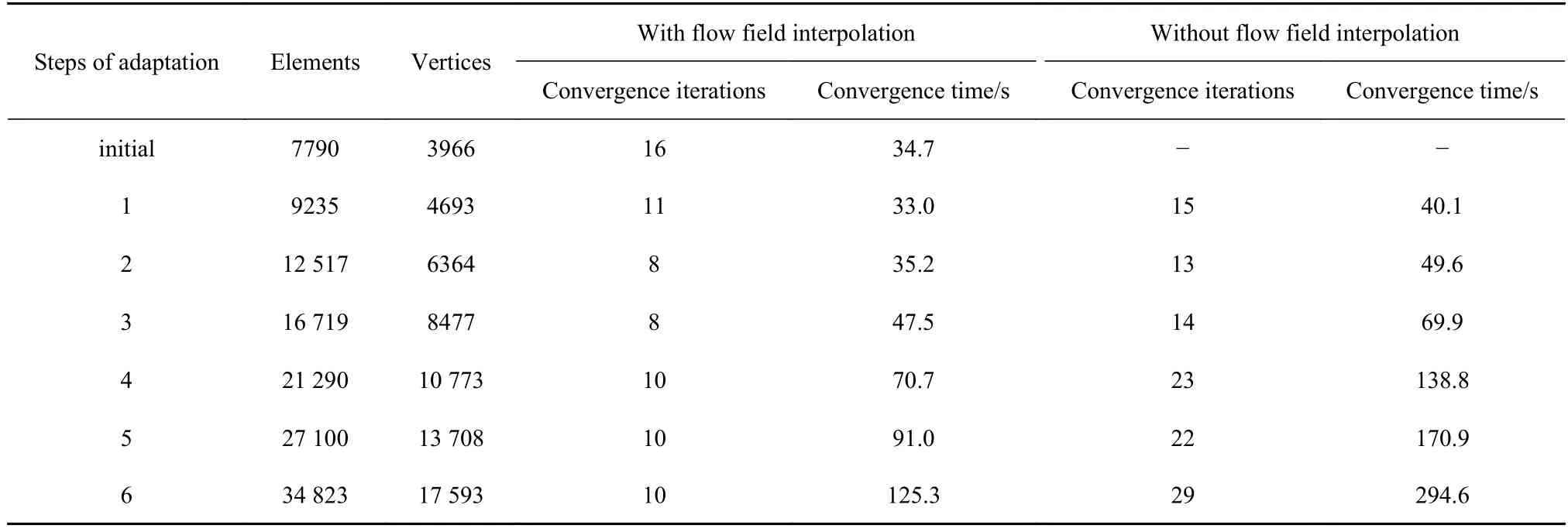
表4 有無流場插值功能時求解收斂情況Table 4 Convergence of solution with or without the flow field interpolation

5 結論

本文提出了一類高精度流場插值方法,實現將前一迭代步網格中流場數值解插值到當前迭代步網格中,以延續前一迭代步中的計算狀態,該插值方法可應用于高階精度自適應流動計算中.為實現流場插值過程中物理量守恒,該方法先計算新舊網格的重疊區域,然后將重疊區域的物理量從舊網格轉移到新網格中.為滿足高階精度要求,先采用kexact 最小二乘方法對舊網格上的數值解進行重構,得到滿足精度要求的物理量分布多項式,隨后采用高斯數值積分實現物理量精確地轉移到新網格的各單元上.最后,通過兩個算例驗證了本文算法的有效性.

本文雖然以二維三角形網格為例闡述高階插值方法,但其思想同樣適應于三維四面體網格情形.不同之處在于,三維情形需要對四面體網格進行求交運算以實現插值過程中物理量守恒,同時插值過程中需要進行體積分計算.下一步的工作,將考慮將本文方法拓展到三維四面體網格的高階流場插值中.