深海采礦系統中懸臂式立管渦激振動分析1)

金國慶 鄒 麗 ,?,2) 宗 智 ,? 孫 哲 王 浩

* (大連理工大學船舶工程學院,工業裝備結構分析國家重點實驗室,遼寧大連 116024)

? (高技術船舶與深海開發裝備協同創新中心,上海 200240)

** (中國水利水電科學研究院,北京 100038)

引言

海底蘊藏著豐富的礦產資源,目前已知的包括多金屬結核物、多金屬硫化物、富鈷結殼和深海稀土資源等,具有重要戰略意義與商業開采價值[1-2].這類礦產資源大多富含于數千米水深的深遠海底部,賦存狀態的特殊性和周圍環境的復雜性導致開采難度較大[3-4].目前主流的深海采礦方式為垂直管道混輸系統,即采用水力提升的方式將礦物通過長距離的管道輸送至水面采礦船.該系統主要由海底采礦系統、垂直輸運系統和水面支持系統三部分組成[3].如圖1 所示,海底采礦車收集礦物并通過軟管輸送到中間倉(緩沖倉),之后利用水力提升泵將礦物通過垂直提升管道輸送至水面母船[5-9].

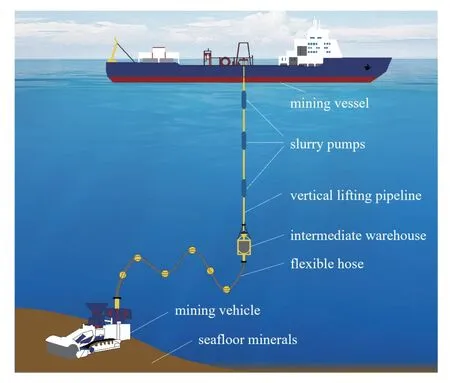
圖1 深海采礦系統示意圖Fig.1 Sketch of the deep-sea mining system

礦產混輸系統中的關鍵裝備之一為具有大長細比特征的垂直提升管道.不同于傳統的海洋立管,垂直提升管道底部與中間倉相連接,其底部是自由運動的狀態,因此該輸運管道通常被稱為懸臂式或自由懸掛式立管.類似的立管形式在油氣資源開采系統中也會遇到,當遭遇極端海況或者回收輸油管道時,輸油管道底部脫離井口,呈現自由懸掛式狀態[10-12].在深海采礦垂直提升管道的研究中,底部中間倉重量可簡化為一個垂直向下的作用力,立管底部可視為弱約束狀態.然而,目前對此類立管的研究主要集中在結構動力學行為分析[11-15],缺乏對其水動力學性能的研究.

與傳統立管類似的是,懸臂式立管在作業過程中也面臨著渦激振動(VIV)等水動力學問題.渦激振動指的是流體經過鈍體結構物,從物體表面分離后在尾部交替地產生旋渦,進而產生周期性的外力和振動.在一個質量-彈簧-阻尼系統中,當振動頻率和瀉渦頻率一致時,出現鎖定共振現象,此時結構物會產生大幅度的振動,嚴重危害作業安全.此外,長期的立管振動會導致結構出現疲勞損傷.因此,立管的渦激振動研究是立管水動力性能分析的重要組成部分.對于立管的渦激振動特性的測量,傳統的做法是采用縮尺模型進行水池試驗.Chaplin 等[16]針對一根長13.12 m 的柔性立管,進行了階梯流作用下的VIV 試驗研究,觀察到了立管在一定流速下被激發出高階模態振動.Trim 等[17]開展了水平布置的38 m 長的立管分別在均勻流和剪切流作用下的試驗,分析了不同拖曳速度下的振動模態和頻率等特征.Song 等[18-19]和高云等[20]研究了7.9 m 長立管在不同流速的均勻流作用下的非均勻分布的水動力載荷、立管截面運動軌跡和疲勞損傷等問題.此外,王俊高等[21]研究了正弦振蕩來流下小尺度模型立管的VIV 特性.徐萬海等[22]則結合拖曳水池試驗和數值模型分析了立管的流體力系數特性.在懸臂式立管模型試驗方面,文獻[10]研究了水面母船運動對立管動力行為的影響.Fujarra 等[23]研究了懸臂式管道在一階振動模態下的鎖定問題.Wang 等[24]分析了船舶周期性運動對自由懸掛式立管運動響應的影響.Mao 等[25]測量了懸掛式排空采油管道在不同流速下的振動模態和振幅.然而,模型試驗成本高且周期較長,此外,縮尺模型需要改變立管的材料屬性,產生難以避免的誤差.

近年來,數值手段成為研究立管渦激振動的主要方式.常見的立管振動預報數值方法主要分為三類:經驗模型、參數化模型和CFD 模型[26].其中,經驗模型常采用尾流振子模型獲得作用在結構上的流體力,進一步通過梁模型求解立管變形[27-29].參數化模型則是基于一系列的剛性圓柱渦激振動試驗結果來確定立管運動幅值[30],該方法已形成相關的計算軟件,例如Shear 7 和VIVANA 等.可以看出,前兩者分別屬于經驗和半經驗方式,因此其計算成本相對較低.計算流體力學方法則是通過求解Navier-Stokes (N-S)方程,獲得立管尾流場的非定常流動特征和時域內變化的水動力載荷.常見的方法是基于切片法的思想,采用CFD 模型求解立管若干節點的受力,通過有限元方法求解柔性立管變形和振動[31-34],這類準三維的數值模擬手段可兼顧計算效率和精度.此外,部分研究采用高精度的大渦模擬LES 方法[35]和直接數值模擬DNS 方法研究低雷諾數下柔性立管的渦激振動[36-37],但該方法目前所需計算資源較大,難以求解高雷諾數下大長細比立管的水動力問題.

綜上所述,基于CFD 模型和有限元的耦合求解算法,可有效求解具有大長細比特征的海洋立管的渦激振動問題.其中,離散渦方法(DVM)[38]作為一種無網格的純拉格朗日的流體計算方法,可以高效率地求解高雷諾數下的圓柱繞流問題,通過與有限元方法(FEM)結合,近年來被發展用于研究立管的VIV 問題[31-32,39-40].此外,目前海洋立管研究主要集中于傳統的兩端鉸支的立管形式,缺乏對深海采礦系統中采用的懸臂式立管水動力性能的研究.本文基于準三維的DVM-FEM 耦合算法,建立懸臂式立管渦激振動的計算模型,即立管上端固定,底部無約束且承受一定的向下的拉力.主要目的是系統性地研究不同流速下懸臂式立管的振動響應,分析其振動模態、頻率和振幅等主要特征.本文首先分別介紹了二維離散渦算法和有限元模型.其次,通過數值預報與經典的9.63 m 長立管在均勻流作用下的試驗結果[41]的對比,驗證了本文采用的耦合算法可以較好地預報柔性立管的振動響應.最后,研究不同折合速度下懸臂式立管的VIV 特征,分析其與兩端鉸支立管的異同.本工作可為深海采礦混輸提升系統的設計和振動行為分析提供參考.

1 DVM-FEM 耦合算法

本文所采用的耦合算法基于切片法的思想,將立管沿垂向劃分成若干切片,在每個切片上通過二維離散渦算法求解彈性圓柱渦激振動問題,并獲得該切片所對應的節點的水動力載荷.此外,基于有限元方法建立柔性立管振動求解的控制方程,通過迭代求解獲得立管振動的時域解.綜上,該耦合算法主要包括流體求解器和結構求解器兩部分,所對應的算法分別為離散渦和有限元方法.

1.1 流體求解器:離散渦方法

離散渦算法是一種純拉格朗日粒子算法,不需要進行復雜的網格劃分,渦元在物面上生成,運動后的渦元主要集中在邊界層和尾流區域,因此具有較低的計算成本[38,42].根據質量守恒和動量守恒定律,離散渦算法的控制方程為連續性方程和N-S 方程,即

式中,u為速度矢量,D/Dt為物質導數,f為質量力,ρ 為流體密度,ν 為運動黏度.對式(2)兩側取旋度,可得到二維渦量輸運方程

式中,ω 是垂直于二維水平面方向上的渦量分量

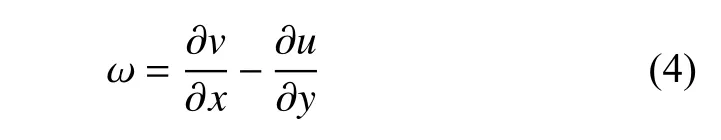
式中,u和v分別是速度在x和y方向上的分量.離散渦方法引入流函數 ψ,速度分量可表示為

將方程(5)代入式(4)中可得Poisson 方程

Chorin[38]采用算子分裂法的思想,將渦量輸運方程分解為兩部分求解,分別為對流和擴散方程

對流項

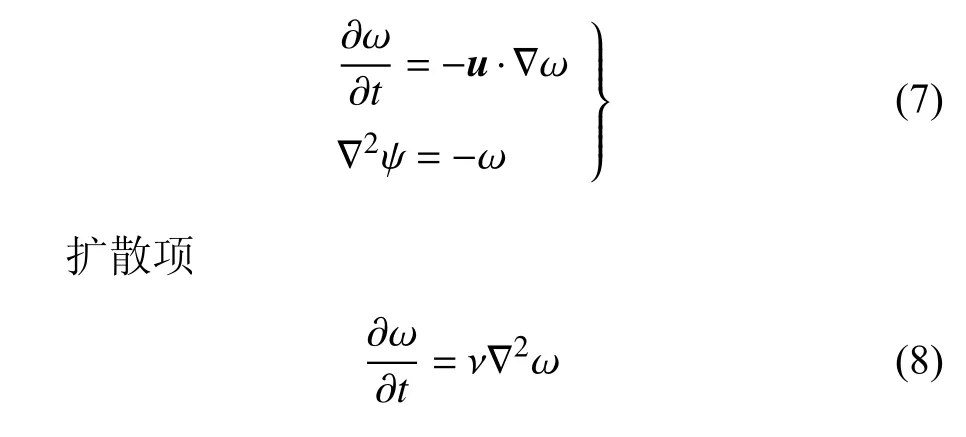
通過Biot-Savart 定律可求解對流項方程,渦元對流速度由渦元之間的誘導速度和來流速度兩部分組成,基于Spalart 等[42]提出的渦核模型,數值計算過程中的對流速度可表示為

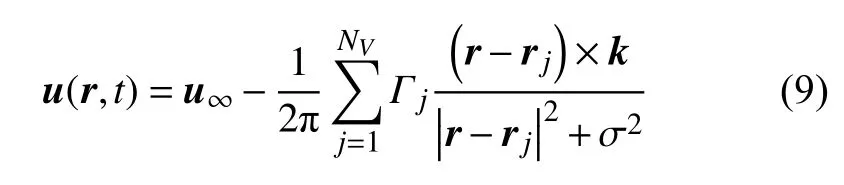
式中,u∞=(u∞,0) 為來流速度,r=(x,y) 為渦元位置坐標,Γ 為渦元強度,σ 為渦元半徑,k為二維平面垂向單位矢量.對于擴散項,基于Chorin[38]提出的隨機擴散法求解擴散方程,即

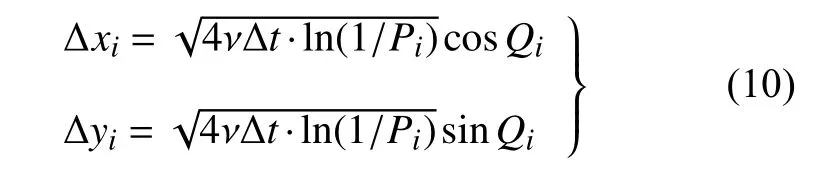
式中,?xi和 ?yi分別為第i個渦元在兩個方向的隨機步長,?t為迭代時間步,Pi和Q分別為介于 (0,1) 和(0,2π)的隨機數.采用二階Runge-Kutta 法進行時間積分,渦元i在t+?t時刻的新位置為

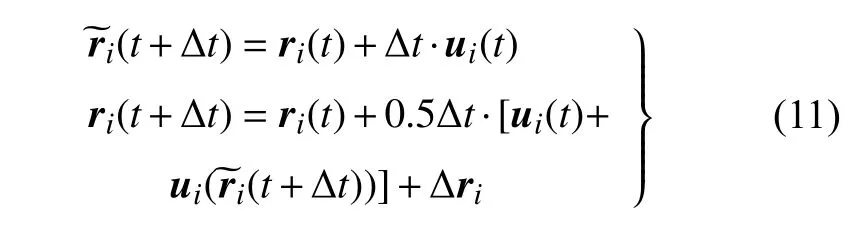
求解物面壓力分布時,由于物體是運動的,因此需在壓力求解中考慮加速度項,即

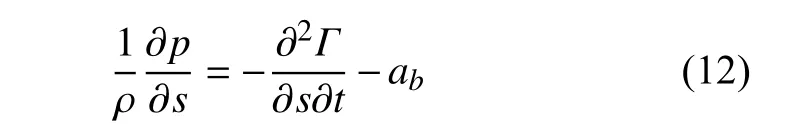
式中,p為物面壓力,s表示物面切向,ab為物體運動加速度.

離散渦算法具體的實現過程可參考文獻[43-44].需要注意的是,渦元在運動過程中會進入物體內部,本文采用瞬態渦量守恒方法,將進入圓柱內部的渦元基于圓周定理映射到物體外部,保證單個時間步內流場渦量是守恒的,具體實現步驟可參考文獻[44-45].

1.2 結構求解器:有限元方法

海洋柔性立管具有大長細比的特征,可簡化為一根垂直的Euler-Bernoulli 梁模型.通過Galerkin 方法,可獲得立管結構動力響應計算的有限元控制方程[31-32],即

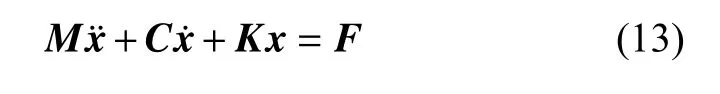
式中,M,C,K分別為質量、阻尼和剛度陣,F為外力矢量,x為立管各節點組成的位移矢量.其中外力矢量由離散渦算法提供,阻尼采用Rayleigh 阻尼模型,即

式中,α 和 β 為瑞利阻尼系數,計算方式為

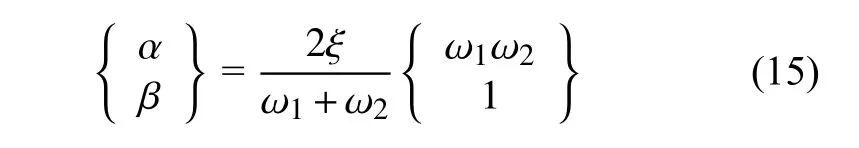
式中,ξ 為阻尼比,ω1和 ω2分別為立管的前兩階固有角頻率,可通過模態分析獲得,本次計算模態分析采用子空間迭代法[46].

需要注意的是,傳統的兩側鉸支立管高度為 2 處的張力T(z) 由頂部張力、包含管內流體重量的立管結構自重和浮力項三部分組成,即

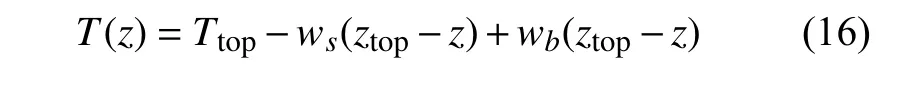
式中,Ttop為頂部張力,ztop為立管頂端高度,ws和wb分別為單位長度立管的自重和所受到的浮力.對于底部有附加重量的懸臂式立管,其所受張力由參考文獻[25-47]給出

式中,Wb為立管底部承受的向下的拉力,即深海采礦系統中中間倉的重量.

如圖2 所示,懸臂式立管可簡化為一個柔性懸臂式模型,其底部連接的中間倉可簡化為一個垂直向下的力Wb,需要注意的是該力學模型忽略了中間倉慣性力的影響.未來工作中可以將中間倉簡化為一個集中質量節點進行結構動力響應分析,并且可以研究這兩種力學模型的異同.

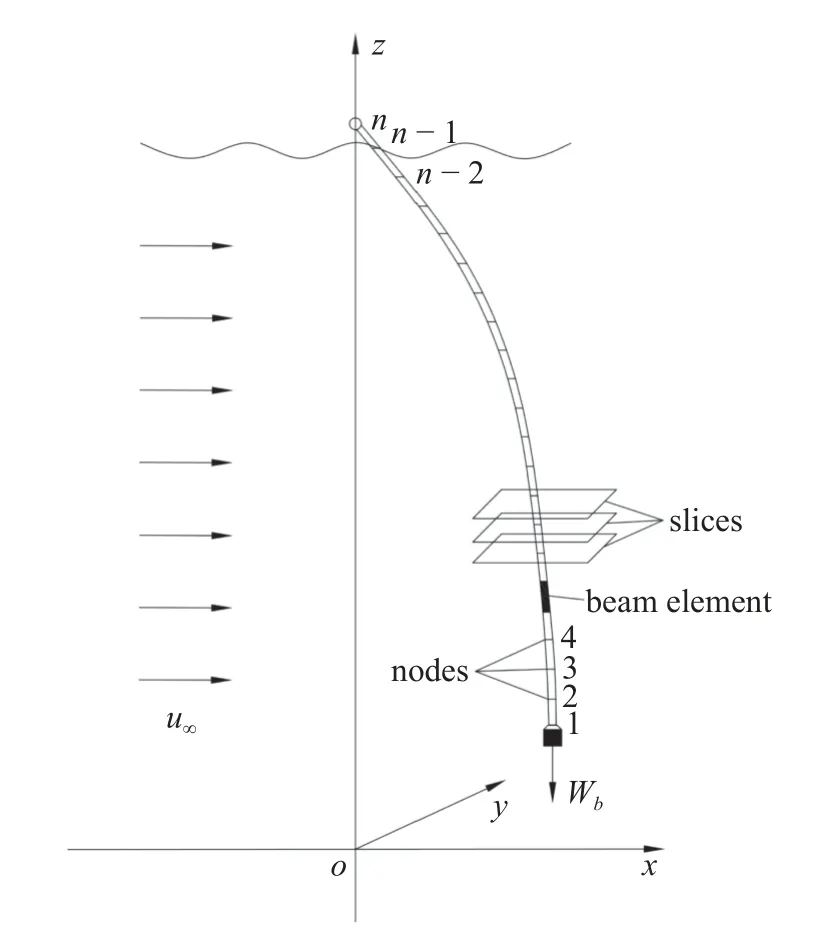
圖2 垂直提升管道簡化模型Fig.2 Simplified model of the vertical lifting pipeline

綜上所示,基于切片法的思想,立管被劃分成一系列的梁單元,基于離散渦方法求解立管各單元節點所受的外力,采用有限元方程求解柔性立管結構變形,本文采用Newmark 方法[46]迭代求解每個時間步內的立管振動位移、速度和加速度,采用弱耦合的形式實現流體和結構求解器之間的數據交換.在接下來的內容中,本文首先通過與經典的立管模型對比來驗證該耦合算法的有效性,進一步分析懸臂式立管的VIV 特性.

2 數值模型驗證

由于懸臂式立管的模型試驗基準算例較少,在這一節中仍采用頂端和底部均為固定邊界條件的模型試驗進行數值驗證.基于DVM-FEM 耦合算法的計算程序由本文作者自主開發,采用Fortran 語言編寫.如表1 所示,物理模型試驗[41]中的立管總長度為9.63 m,立管外部直徑為20 mm,厚度為0.45 mm,頂部張力為817 N,分別計算均勻流速0.42 m/s 和0.84 m/s 兩個流速下的立管振動響應.

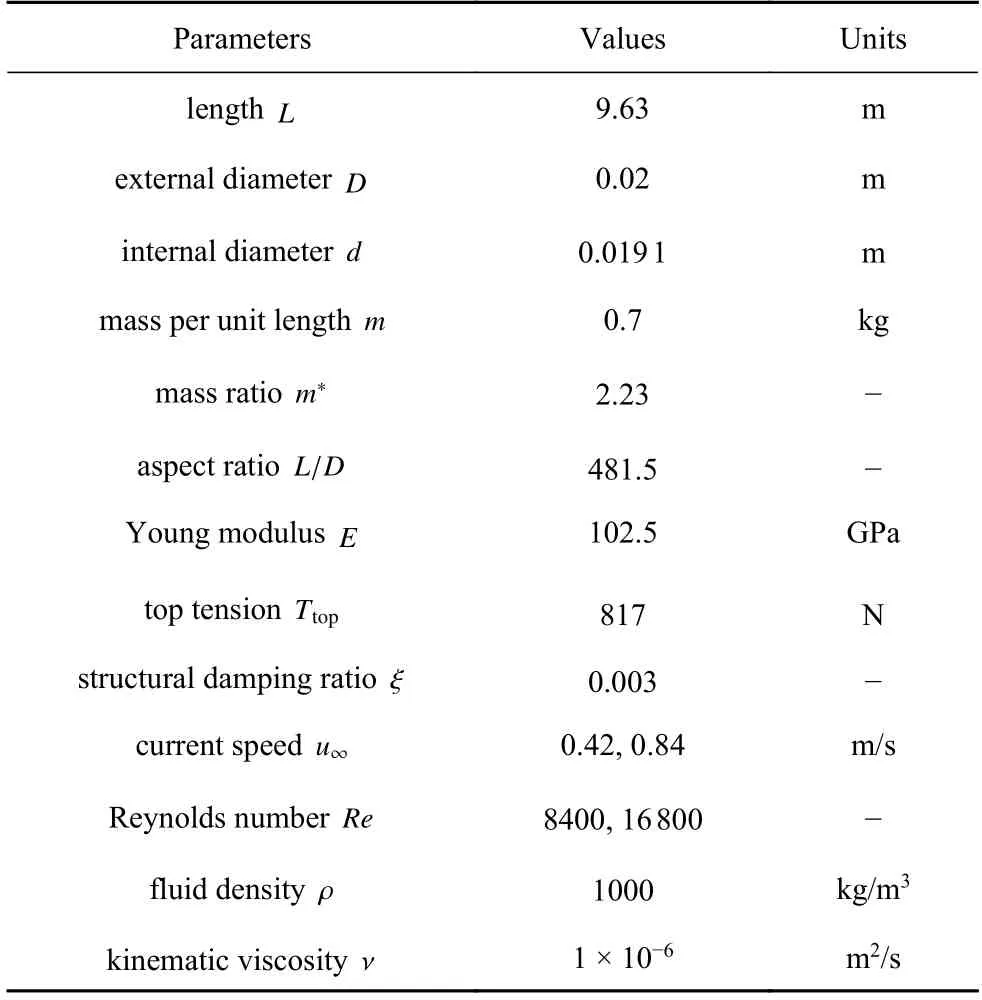
表1 柔性立管參數[32,41]Table 1 Parameters of a flexible riser[32,41]

本文的耦合算法基于切片法,切片數量對計算成本有重要影響,選取合適的立管單元數N可在保證計算精度的基礎上提高求解效率.本次研究選擇了4 套立管單元數進行敏感性分析,數量分別為30,60,90 和120.在0.42 m/s 來流速度作用下,不同單元數計算得到的立管橫向振動位移均方根值如圖3 所示.可以看出,立管單元數量變化對其振幅和模態的影響均較小,選取N=60 時即可滿足立管單元數量收斂性要求,因此本文所有模擬采用的立管單元數均為60.

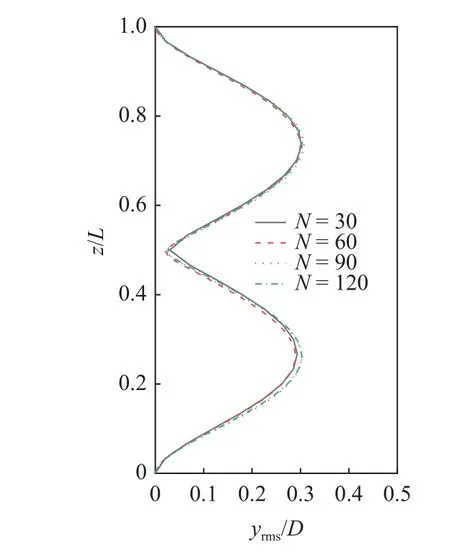
圖3 不同單元數立管的橫向位移均方根值Fig.3 RMS amplitudes of the transverse displacements for the riser models with various element numbers

兩個來流速度下的立管在不同時刻的橫向振動位移包絡線和對應的均方根值如圖4 所示.可以看出,在0.42 m/s 流速下,立管橫向呈現出2 階振動模態.高流速下激發出了更高階的振動模態,在0.84 m/s 流速作用下,立管橫向振動呈現出4 階模態.進一步對比橫向振動位移的均方根值,如圖4(b)和4(d)所示,圖中同時給出了文獻[32,48-49]的數值模擬結果.結果表明:數值預報的振動模態階數與試驗和其他數值模擬結果均是一致的,但振動幅值相比試驗結果是偏小的,目前算法在準確預報柔性立管振動幅值方面仍有待改進.本文數值模型預報立管振幅偏小的原因可能是多方面的,首先,DVMFEM 耦合算法基于切片法的思想,將立管簡化為梁模型進行結構動力響應求解,忽略了立管本身三維效應的影響以及尾流中三維渦結構的影響,Huang等[48]和Wang 和Xiao[49]則是采用完全三維網格的方法求解流場和立管變形;其次,Wu 等[50]的研究表明立管流向和橫向運動之間存在相互作用,本文采用的耦合算法則是單獨求解每個方向的立管結構動力響應;此外,離散渦方法本身及其與有限元方法的耦合方式仍有待進一步的研究與改進.

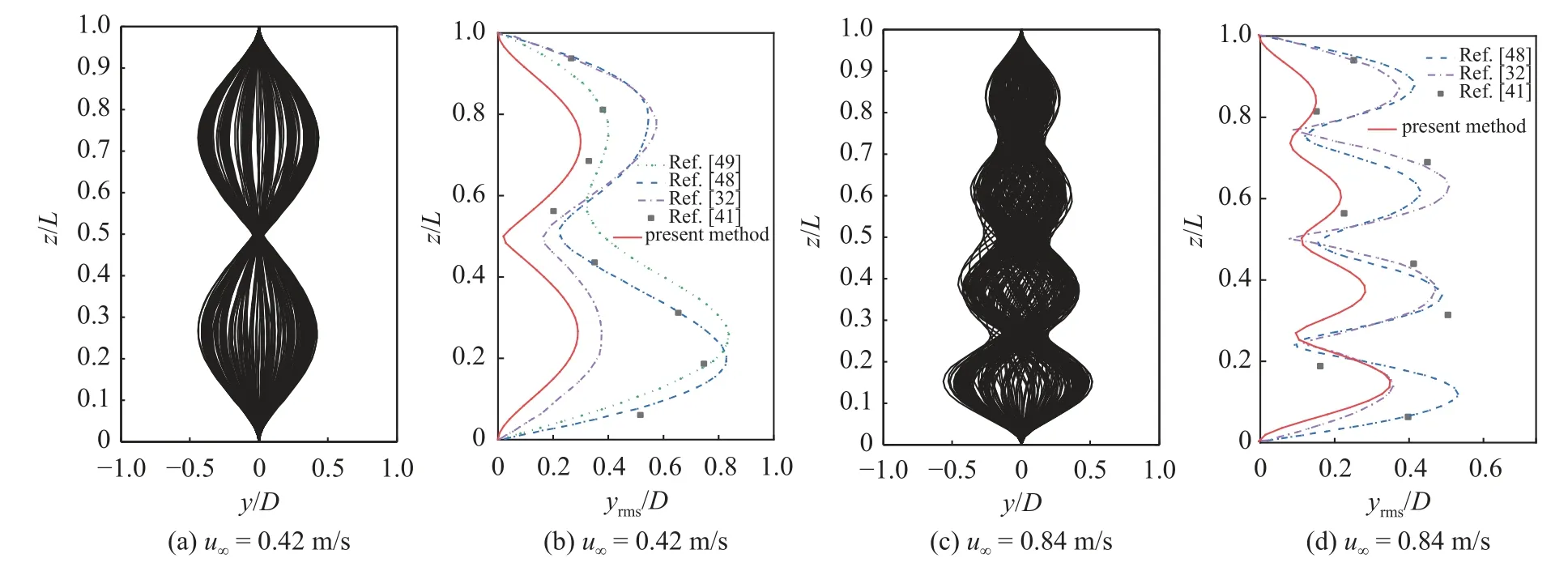
圖4 不同流速下的柔性立管橫向振動響應((a),(c)振動位移包絡線;(b),(d)位移均方根值)Fig.4 Vibration response envelopes of a flexible riser under different current speeds ((a),(c) vibration amplitude envelopes;(b),(d) RMS displacements)

3 懸臂式立管計算結果與分析

本節主要關注不同流速下的懸臂式立管的渦激振動響應特征,同樣選用上述9.63 m 長的立管,其底部承受的向下的拉力設定為Wb=817 N,這與原來兩端鉸支的立管試驗中所選擇的頂部張力在數值上是相同的,其他物理參數保持不變.因此,不同流速作用下的柔性立管的固有頻率是一致的.基于子空間迭代法可獲得立管濕模態下的前8 階固有頻率及其對應的歸一化的振型,如圖5 所示.立管的固有頻率隨模態階數的增加而增大,本文以1 階固有頻率f1=0.78 Hz 為參考值,取折合速度Ur從4 到46,間隔為2,計算得到的實際流速區間為u∞=0.0626～0.6884,對應的雷諾數區間為Re=1252～ 13768.折合速度計算公式為

圖5 懸臂式立管前8 階固有頻率和振型Fig.5 First eight-order natural frequencies and modal shapes for a cantilever riser

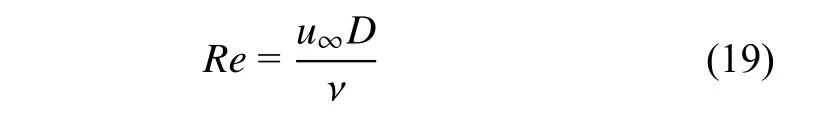
雷諾數計算公式為

基于結構物繞流的升力時歷曲線,采用快速傅里葉變換(FFT),可得到泄渦頻率fs,進一步可計算斯特勞哈爾數

3.1 振動響應分析

首先,本文計算了不同折合速度下的柔性懸臂式立管的橫向振動,振幅均方根值隨Ur和z/L的變化情況如圖6 所示.可以看出,隨著折合速度的增加,立管振動模態逐漸增加,在較高折合速度下高階模態被激發.在Ur=4～ 46 范圍內,橫向振動逐漸由1 階模態向4 階模態過渡.立管振幅則呈現出波浪式的變化特征,即在一定的折合速度范圍內,立管的振動模態是相同的,這與Fan 等[35]對兩端鉸支柔性立管VIV 的研究結果類似.當立管呈現出相同模態時,隨著Ur的增加,立管振幅逐漸增加,同時在少數折合速度下振幅沒有呈現出線性增長的特征.當振動從低階模態向高階模態轉變時,模態階數的躍遷過程中會伴隨著振幅的突然降低.此外,可以很明顯地觀察到無約束的立管底部表現出較大幅度的位移.

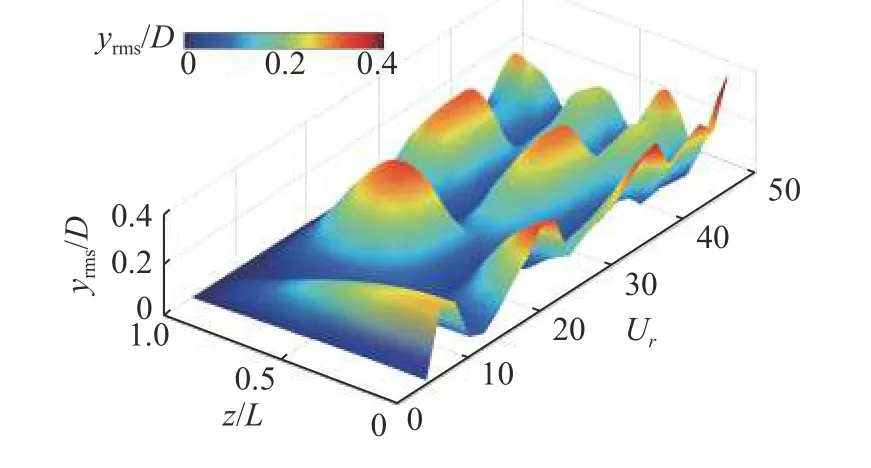
圖6 不同折合速度下的橫向振幅均方根值Fig.6 RMS vibration amplitudes in the transverse direction under a wide range of reduced velocities

針對不同振動模態下立管的變形特征,本文分別將1 階到4 階模態下立管橫向振動的位移均方根值進行了比較分析,如圖7(a)到圖7(d)所示.并且列舉了四種振動模態下某一折合速度對應的立管瞬態振動包絡線圖,如圖7(e)到圖7(h)所示.同樣可以看出,大部分情況下,沿立管展向各位置處的橫向位移隨折合速度增加而逐漸增大,該變化特征在3 階模態情況下最為明顯,如圖7(c)所示.此外,在同一振動模態下,振幅最小處所對應的立管展向位置基本上是相同的,與來流速度關系較小.

圖7 不同折合速度下的柔性立管橫向振動響應 ((a)～(d)位移均方根值;(e)～(h)振動位移包絡線)Fig.7 Vibration response envelopes of a flexible riser under different reduced velocities ((a)～(d) RMS amplitudes;(e)～(h) vibration amplitude envelopes)

在深海采礦系統中,懸臂式立管底部與中間倉相連接,礦物經輸料軟管到達中間倉,再通過垂直提升硬管輸送到水面母船.因此,立管底部的振動對礦物輸運的穩定性有較大的影響.本文將中間倉簡化為有一個作用在立管底部的垂直向下的作用力進行研究,如圖2 所示.由上述分析可知,懸臂式立管底部位置有較大幅度的位移,不同折合速度下的立管底部位移均方根值如圖8 所示.可以看出,不同模態下振幅的增長速率是不同的.在同一振動模態下,立管底部振幅與折合速度基本上呈現出線性關系.

圖8 立管底部橫向位移均方根值Fig.8 RMS amplitude of the transverse displacement at the bottom for the riser

不同折合速度下立管振動的主導頻率fv如圖9 所示.圖中St=0.2 這條線表示當圓柱在亞臨界雷諾數范圍內振動時,其對應的斯特勞哈爾數位于0.2 附近[51].整體上,振動頻率隨著折合速度的增加而逐漸增大.當振動模態發生轉換時,振動頻率會發生突然的跳躍.在同一振動模態內,振動主導頻率在低折合速度下沿著St=0.2 增加,且頻率值低于所對應振動模態下的固有頻率.隨著折合速度進一步增加,當振動頻率超過固有頻率后,主導頻率逐漸偏離S t=0.2 所對應的頻率值,該現象與剛性圓柱渦激振動是類似的[52].

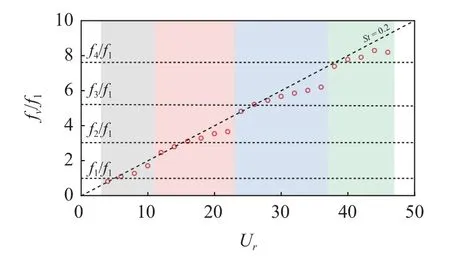
圖9 橫向振動的主導頻率比Fig.9 Dominant frequency ratio of the transverse vibration

3.2 三階模態下橫向振動響應分析

由上文分析可知,懸臂式立管發生渦激振動時,其振動模態在一定折合速度范圍內是相同的,因此本節選取典型的3 階振動模態進行討論.本文中立管以3 階模態振動時所對應的折合速度Ur=24～36,間隔為2,共7 個工況,所對應的橫向振幅均方根值如圖7(c)所示.基于立管垂向不同位置振動時歷曲線,采用快速傅里葉變換(FFT)方法對時歷數據進行頻譜分析,可得到振動頻率的空間分布特征,如圖10 所示.其中顏色條為歸一化的振動能量譜密度(PSD),白虛線表示3 階振型所對應的固有頻率,f3=4.07 Hz.可以看出,7 種折合速度對應的振動頻率均由3 階模態主導,且不同折合速度下立管底部均呈現出較高能量的振動.此外,隨著折合速度增加,振動頻率逐漸遠離3 階固有頻率.

同樣采用FFT 方法,可得到不同折合速度下的立管展向各位置處的泄渦頻率空間分布,如圖11 所示,其中白虛線均表示St=0.2 所對應的頻率值.與圖10 相比,不同折合速度下泄渦頻率與振動頻率基本上是一致的.在低折合速度下,立管各位置處的泄渦頻率均集中在St=0.2 附近,隨著速度增加,立管展向大部分位置所對應的泄渦頻率逐漸低于S t=0.2所對應的頻率值,盡管仍有較少位置的泄渦頻率集中在St=0.2 附近.不同折合速度下的泄渦頻率在立管展長方向上并未呈現出明顯的分布特征,這與振動頻率空間分布圖中呈現出的3 階分布特征是不同的.

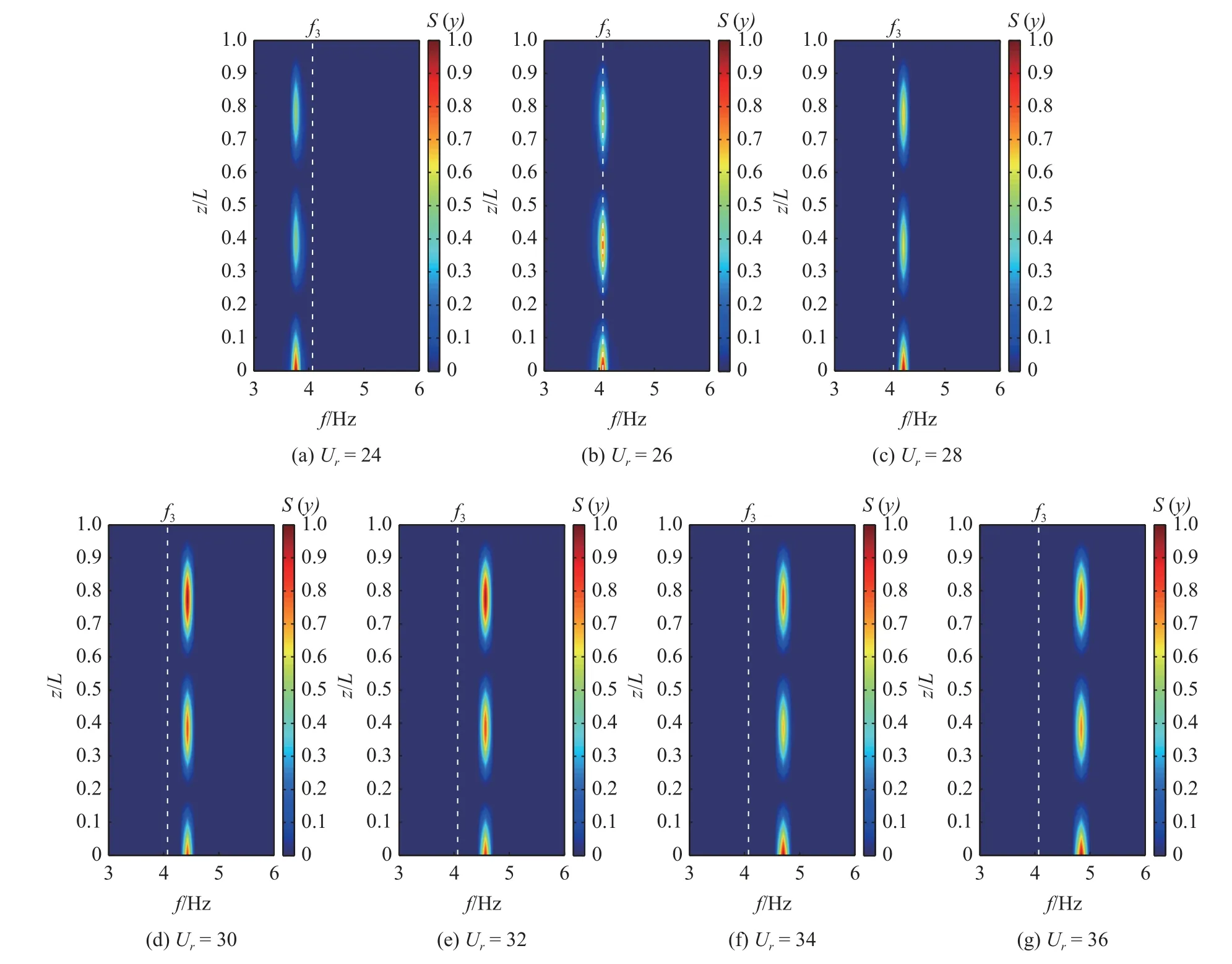
圖10 立管橫向振動頻率空間分布 ((a)～(g) Ur=24～36)Fig.10 Spatial distribution of transverse vibration frequency for the riser ((a)～(g) Ur=24～36)

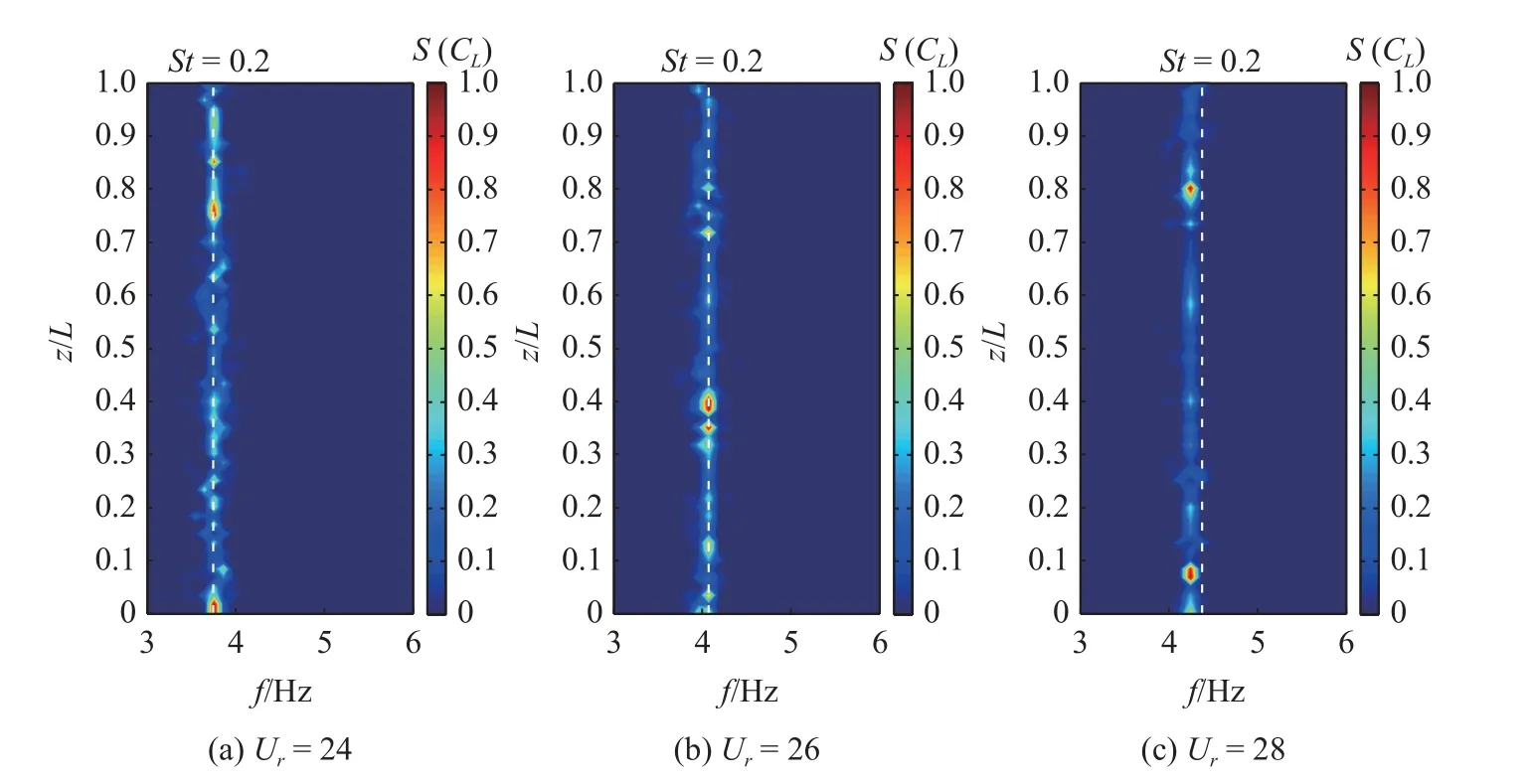
圖11 立管泄渦頻率空間分布 ((a)～(g) Ur=24～36)Fig.11 Spatial distribution of vortex shedding frequency for the riser ((a)～(g) Ur=24～36)

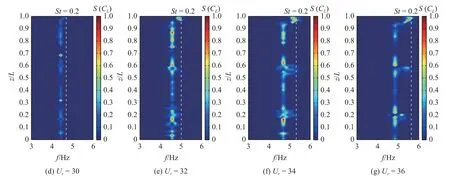
圖11 立管泄渦頻率空間分布 ((a)～(g) Ur=24～36) (續)Fig.11 Spatial distribution of vortex shedding frequency for the riser ((a)～(g) Ur=24～36) (continued)

3 階振動模態下不同折合速度所對應的立管橫向振幅時空演化特征如圖12 所示,所有時空演化圖選擇的時間段均為6～8 s,其中紅色和藍色表示相反的振動方向.可以看出,隨著折合速度的增加,立管展向不同位置處的振幅增加,且在該時間段內駐波特征逐漸增強.由上文分析可知,同一振動模態下,振動頻率隨折合速度的增加而增大,因此相同時間段內紅藍單元交替的周期逐漸減小.

圖12 立管不同位置的振幅時空演化 ((a)～(g) Ur=24～36)Fig.12 Temporal-spatial evolution of transverse vibration amplitude along the riser span ((a)～(g) Ur=24～36)

本文工作基于切片法的思想,在切片上采用無網格的二維離散渦算法計算流體力,四種折合速度下(Ur=24,28,32,36)的立管若干截面處的瞬態渦量場如圖13 所示.可以看出,隨著折合速度的增加,立管底部的流向位移逐漸增大.立管不同高度截面渦量場中紅色和藍色粒子分別表示渦元具有正向和負向的渦量.立管不同截面處的尾流場中的渦結構具有不同的模式[53],其中大部分截面呈現出2 S 的尾渦模式.此外,近尾流場渦結構比較清晰,而遠尾流場則演化出更為復雜的渦結構特征.

圖13 瞬態渦量場 ((a)～(d) Ur=24～30)Fig.13 Instantaneous vorticity field ((a)～(d) Ur=24～36)

3.3 兩端鉸支與懸臂式立管的渦激振動特征比較

為了比較傳統的兩端鉸支立管(對應海洋工程中的采油管道)與懸臂式立管(對應深海采礦的提升管道)渦激振動特征的異同,本文計算了一系列均勻流速作用下的兩端鉸支的9.63 m 長立管的渦激振動響應.立管頂部張力與試驗保持一致,取為Ttop=817 N.立管濕模態下的前8 階固有頻率及其對應的歸一化的振型,如圖14 所示.可以看出,兩端鉸支立管的各階固有頻率均大于對應的底部拉力為817 N 的懸臂式立管的固有頻率.兩端鉸支立管的1 階固有頻率f1=1.61 Hz,本次計算取折合速度Ur=4～ 44,間隔為2.計算得到的不同來流速度作用下立管最大的橫向位移均方根值如圖15 所示,圖中不同顏色塊表示不同的振動模態.可以發現,橫向振幅的變化規律與懸臂式立管是一致的,即在同一振動模態下,立管振幅與折合速度基本上呈現出線性關系.此外,當模態轉變發生時,振幅會突然降低,并隨著折合速度增加,振幅再一次逐漸增大,這與懸臂式立管的VIV 特征也是相同的.

圖14 兩端鉸支立管前8 階固有頻率和振型Fig.14 First eight-order natural frequencies and modal shapes for a riser hinged at both ends

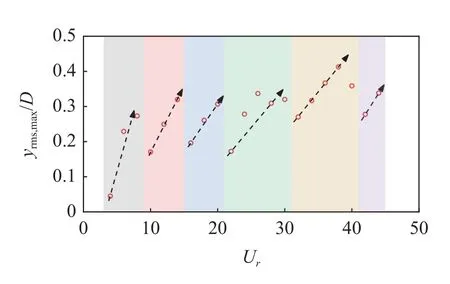
圖15 沿立管展向最大的橫向位移均方根值Fig.15 Maximum RMS amplitude of the transverse displacement along the riser span

橫向振動的主導頻率與1 階固有頻率的比值如圖16 所示.同樣地,振動頻率的變化趨勢與懸臂式立管也是一致的,即振動頻率隨著折合速度的增加而逐漸增大,并且當振動模態改變時,振動頻率會出現較大幅度的增加.不同的是,在相同的折合速度區間內,兩端鉸支立管存在6 階振動模態,而懸臂式立管只存在4 階模態.這是由于兩端鉸支立管的1 階固有頻率較大,相同折合速度下其對應的真實來流速度更大,這導致兩端鉸支立管被激發出高階模態響應.本文選取兩端鉸支立管的3 階振動模態進行分析,該模態下3 個不同折合速度作用下的立管不同位置的振幅時空演化如圖17 所示,選擇的時間段均為5～7 s.可以發現,兩端鉸支的立管展向不同位置處的振幅均隨折合速度增加而增大.在低階模態響應下,隨折合速度增加,該時間段內駐波特征逐漸增強.這兩個特征與懸臂式立管是一致的.

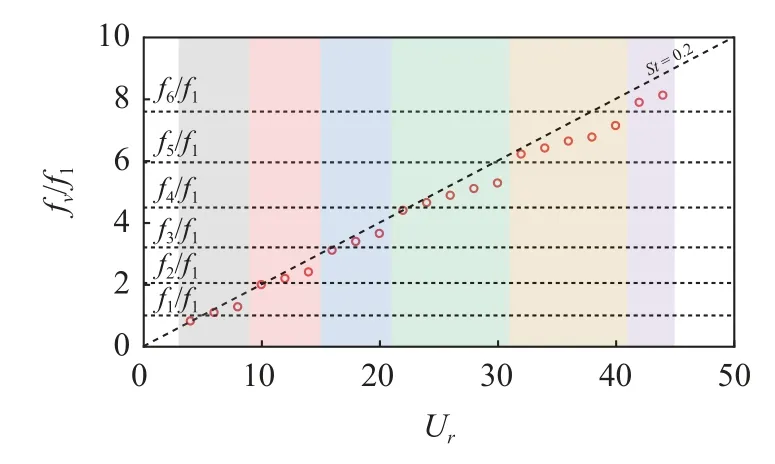
圖16 立管橫向振動的主導頻率比Fig.16 Dominant frequency ratio of the transverse vibration for the riser

圖17 立管不同位置的振幅時空演化 ((a)～(c) Ur=16～20)Fig.17 Temporal-spatial evolution of transverse vibration amplitude along the riser span ((a)～(c) Ur=16～20)

4 結論

礦產混輸垂直提升管道是深海采礦集成系統中十分重要的裝備,其懸臂式的結構面臨復雜海洋環境時的振動特征不同于傳統海洋立管,目前文獻仍缺乏對該類型立管的討論.本文的主要目的便是分析具有一定底部重量的懸臂式立管在不同來流速度下的渦激振動響應.為此,本文首先建立了基于切片法思想的DVM-FEM 耦合模型,通過數值計算兩端鉸支立管的振動響應并與模型試驗結果對比,驗證了該耦合模型的有效性.最后,系統性地分析了不同速度的均勻來流作用下懸臂式立管的橫向振動響應特征,主要結論如下.

(1)本文采用的DVM-FEM 耦合算法可以準確預報柔性立管在不同速度下的振動模態,但振幅相比試驗結果要小,該問題同樣出現在前人的研究工作中[39].由于本文目的是研究深海采礦系統中存在的懸臂式立管的渦激振動特征,因此目前工作主要分析不同來流速度對這類特殊立管的影響規律,如何實現對立管實際振幅的準確預報仍有待進一步的研究.

(2)對于懸臂式立管,隨著折合速度的增加,立管的振動模態階數逐漸增加.同時,振動模態在一定的折合速度范圍內是相同的.在同一模態下,立管不同位置的振幅隨著速度增加而增大,尤其是無約束的立管底部會發生較大的位移.此外,當模態發生轉換時,振幅會發生突降,并隨著速度的增加振幅再一次逐漸增大.振幅隨Ur和z/L的改變整體上呈現出波浪式的變化特征.

(3)深海采礦垂直提升立管底部與中間倉及輸送軟管相連接,因此底部位移對采礦系統整體穩定性有重要影響.本文結果表明,在同一振動模態下,懸臂式立管底部位移呈現出隨折合速度線性變化的特征.當振動模態發生轉變時,振動主導頻率存在突然跳躍的特征.

(4)本文重點分析了3 階振動模態下的懸臂式立管的振動響應.可以看出,振動主導頻率在低折合速度下低于3 階固有頻率,隨著速度增加,振動頻率逐漸增大并遠離3 階固有頻率.此外,無約束的立管底部的振動能量較大.對于本次研究中3 階模態振動下的懸臂式立管,其駐波特征隨著折合速度增加而逐漸加強,需要注意的是,本文關注的立管模型的長徑比較小且為低階模態響應,對于實尺度深海采礦立管以及高階振動模態響應下的立管,其振動特征仍需進一步研究.

(5)本文對比了懸臂式立管與兩端鉸支立管的異同.可以發現,懸臂式立管的各階固有頻率均小于對應的兩端鉸支立管的固有頻率.在相同折合速度區間內,兩端鉸支立管被激發出更高階的振動模態響應.此外,兩種類型立管的VIV 振幅和頻率隨折合速度的變化規律是相同的.

(6)垂直管道水力提升系統是深海采礦的主流方式,但目前仍缺乏對這類特殊的底部弱約束立管的數值與試驗研究工作.未來研究工作可以考慮以下幾方面:母船運動對懸臂式立管渦激振動和水動力性能的影響;中間倉重量改變的影響;考慮中間倉慣性力作用下的深海采礦立管模型的結構動力響應;海洋剪切流動等變化的影響;考慮內部流動的立管振動特征;采礦立管渦激振動抑制措施等.