基于消卷積的三維成像雷達散射截面測量技術

任雯欣， 廖可非,2*， 任浩田

(1.桂林電子科技大學信息與通信學院， 桂林 541004； 2.桂林電子科技大學衛星導航定位與位置服務國家地方聯合工程研究中心， 桂林 541004)

雷達散射截面積(radar cross section，RCS)是衡量目標在電磁照射下沿接收方向散射回波能力的物理量，表征了雷達目標的散射能力。它會隨雷達的信號頻率，極化方式以及入射角度的變化而變化，并且與目標的形狀，大小，以及結構和材料有關[1]。隨著科學技術的不斷發展，對RCS的精確測量與預估提出了更高的需求。

傳統的RCS測量主要分為室外遠場測量[2-3]、室內緊縮場測量[4]和近場成像測量[5-6]，但在實際測量中，遠場測量條件不易滿足，緊縮場測量價格昂貴，為克服測量距離的限制，基于近場成像測量技術得到了廣泛關注，該種方法基于成像技術獲得目標圖像再提取圖像中的散射中心[7-8]，最終反演得到RCS。這些方法主要分為基于逆合成孔徑雷達成像的RCS測量[9-10]和基于合成孔徑雷達成像的RCS測量[11-12]。Broquetas等[9]提出了一種基于目標表面散射場聚焦算子的近場球面波ISAR成像算法。Lahaie[10]通過反射率近似值對目標散射進行建模以及逆合成孔徑雷達(inverse synthetic aperture radar，ISAR)成像。Tulgar等[11]提出了一種聚束是SAR成像算法，通過獲得目標的SAR圖像再提取相應的RCS。Sensani等[12]介紹了一種由雷達圖像的近場到遠場(NF2FF)處理程序，有利于加深對RCS散射機理的理解。Kobayashi等[13]提出了一種改進的圓柱掃描的近遠場變換方法，該方法使用了小球從精確積分方程中獲得的聚焦因子，使在微波暗室中也可進行RCS測量。Wang等[14]設計了一個二維掃描系統，該系統可以獲取目標的近場三維散射系數圖像。許鑫等[15]提出了一種基于線性調頻信號的壓縮感知雷達成像算法，可得到高分辨的圖像。目前基于成像的RCS測量已有廣泛研究[9-17]，但對合成孔徑三維成像的RCS測量現在還沒有廣泛的研究和應用。進一步研究合成孔徑三維成像的RCS測量更好分析RCS特征、旁瓣抑制以及提高成像質量對于RCS的精確反演有著重要意義。

基于傳統的近場成像方法，由于旁瓣多是由假目標引起的，傳統的消除噪聲，抑制旁瓣的方法有閾值法和加窗法，然而，這兩種方法都有局限性，會導致目標圖像失真從而導致通過反演得到RCS缺乏分辨率。因此需要考慮用其他算法來有效抑制圖像旁瓣。

基于上述問題，針對旁瓣抑制的三維成像RCS測量技術展開研究，提出了兩種主要的抑制旁瓣的算法：一是基于改進CLEAN算法[18]的旁瓣抑制；二是基于壓縮感知成像的旁瓣抑制方法。然后分別從抑制原理和仿真結果兩方面對上述方法進行對比。

1 RCS測量模型

1.1 測量模型

采用線陣合成孔徑的三維成像RCS測量模型為例進行說明，成像模型如圖1所示。在三維坐標xyz下建立成像場景，在二維平面上通過陣元的移動，等效合成二維的平面陣列，同時結合寬帶信號來獲得目標的三維分辨能力。

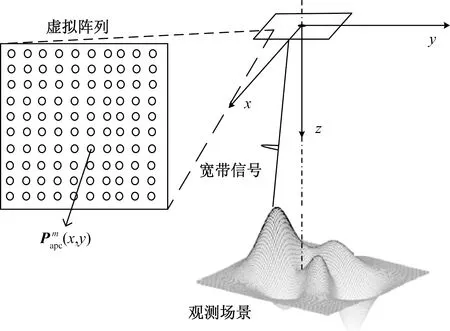
表示所形成的虛擬陣列的第m個陣元

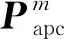
(1)

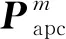
將式(1)回波信號寫為矩陣形式，可表示為

Y=Φ

(2)

(3)

式(3)中：φmn為一個列向量，可表示為

(4)

后像投影成像BP可表示為

BP=ΦTΦ*

(5)

式(5)中：Φ*為式(3)矩陣Φ的共軛；ΦT為Φ的轉置。

獲得目標的三維成像后，從成像當中提取目標的散射中心，之后通過近遠場變換得到遠場的散射函數，最后通過定標法求解遠場RCS，通過RCS反演，可以從三維合成孔徑雷達(synthetic aperture radar，SAR)圖像中恢復出目標遠場不同角度、不同頻率的RCS。

1.2 旁瓣分析

一般信號頻譜中的旁瓣主要為有限長度信號的截斷效應所帶來的，雷達在一維距離像上，基于其有限的信號帶寬，頻譜函數近似為矩形函數，對其作逆傅里葉變換，即為Sinc函數，而Sinc函數含有旁瓣。同理，雷達在方位上也是等效合成了一定的方位帶寬。因此雷達成像當中的旁瓣來源于有限帶寬信號的截斷效應，而截斷效應會帶來兩個方面的影響，一個是泄露，具體表現在雷達成像中是理想分辨函數的展寬，從而降低了圖像的分辨率。另一個是譜間干擾，由于旁瓣的影響，在雷達成像中會造成強點附近的弱目標被掩蓋，或者誤將強點的旁瓣當作目標。因此降低圖像的旁瓣對成像質量的提高至關重要。傳統的抑制旁瓣的方法有閾值法和窗函數法，加窗法通過加權系數，提高主瓣能量，降低副瓣能量，來降低有限信號帶寬的截斷效應。但是傳統的加窗旁瓣抑制方法一定程度上會展寬主瓣，導致圖像分辨率的降低，因此在分辨率和峰值旁瓣比上需要折中考慮。閾值法基于不同閾值提取散射信息，當閾值較小時，會將成像中的旁瓣信息提取出來，當閾值較大時，導致成像當中部分散射信息會丟失，造成RCS的反演誤差。

2 基于旁瓣抑制的新方法

2.1 改進CLEAN算法旁瓣抑制的RCS測量

當場景目標變多變復雜時，利用傳統CLEAN算法抑制旁瓣時誤差較大，這極大的影響著RCS的測量精度，因此考慮采用改進的CLEAN算法抑制圖像的旁瓣，來完成對目標散射中心的提取，提高RCS的測量精度。

改進CLEAN算法利用已有的估值信息，來逐個更新需要重估的點，從而提高估計精度，達到抑制旁瓣的目的。

PSFi表示第i個散射點在整個空間的BP像，可表示為

PSFi=Φ(·,i)TΦ*

(6)

式(6)為該點的點擴展函數，其中Φ(·,i)為矩陣Φ的第i列。

傳統成像都是由真實的散射系數卷積上點擴展函數來獲得也可以展開來寫，即不同的散射系數乘上其對應的點擴展函數再求和，即

(7)

式(7)中：σi為第i個散射點的散射系數，σi=1；N為滿足成像場景中的所有散射點個數。

改進CLEAN算法每次尋找的估計值，不僅影響著此次的精度，也影響著其余散射系數的估計精度，只有盡可能的將每次的估計誤差變小，才能保證更好的估計其余的散射系數。假設獲得了全場景的散射系數估計，則殘差為

(8)

當迭代減法得到的“臟”圖達到某一閾值或已經估計的散射點數達到設定的條件時，對這些點進行重新估計，并用重新估計的值，逐個更新其余的值，從而減弱相干CLEAN算法帶來的累計誤差。成像場景中各個點的BP像是由該點的像與其他目標在該點處的旁瓣干擾組成，改進CLEAN算法抑制旁瓣的過程就是消卷積的過程，散射系數與非理想點擴展函數的卷積運算會造成譜間干擾，強弱目標混淆，通過不斷從“臟”圖中尋找最大值，獲得點散射系數估計，消去該估計的旁瓣影響。

2.2 壓縮感知旁瓣抑制的RCS測量

傳統的奈奎斯特時域等間隔采樣，使得信號在頻譜上進行周期延拓，如果采樣率不滿足信號帶寬的兩倍，則會發生頻譜混疊，而壓縮感知的非等間隔采樣和隨機稀疏采樣使得頻譜搬移不再是周期有序的搬移，使得頻譜泄露的能量能隨機和近似均勻的分布在整個頻率軸上，不再產生周期有效的疊加和干擾。

壓縮感知的成功應用，信號需要滿足稀疏性，即“K稀疏”，對于一個Nd維離散信號，Nd個元素值中只有K個是非零的，其中K?Nd，則稱這個信號是K稀疏的。基于信號的稀疏先驗假設，從稀疏域上經過非周期搬移后的信號即稀疏觀測后的信號，在稀疏域上只有離散的少量峰值存在，壓縮感知重構算法如匹配追蹤算法就是從該信息中逐個求解出相應強點，再減去該點對應的干擾，從而可以從信號當中逐個恢復出有效的強散射信號，而恢復的過程中，將一些低于某個閾值或者在噪聲電壓水平附近的點舍去，即將其置之為零。

壓縮感知抑制旁瓣的核心思想是通過反卷積消除點擴展函數的影響。以下通過表達式對壓縮感知抑制旁瓣進行解釋。

設某單散射點坐標為，根據拋物線近似，陣元與目標散射點距離的表達式為

(9)

進行匹配濾波和距離徙動矯正并經去調頻處理后得到的回波信號用卷積形式表示為

(10)

當信號具有稀疏特性時，可以利用壓縮感知技術去除卷積核，對經過距離壓縮之后的回波信號去除卷積核后進行方位向匹配濾波，利用1D-FFT獲取水平方向壓縮圖像表達式為

(11)

當信號具有稀疏性時，可除去卷積核。再對式(11)進行1D-FFT獲取垂直方位向壓縮圖像得到

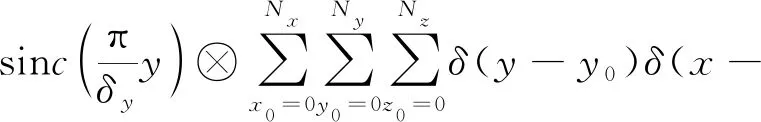
(12)

當信號具有稀疏性時，可除去卷積核后對式(12)進行重建，當場景目標散射系數足夠稀疏時，可以完全消除3維點擴展函數的影響，可以在一定程度上抑制旁瓣。

通過對改進CLEAN算法與壓縮感知算法旁瓣抑制原理上分析，得出了兩種方式的相同與不同之處。兩者抑制旁瓣的原理都是通過消卷積，消除點擴展函數的影響，而不同在于壓縮感知恢復重建的過程是在對原始信號稀疏采樣后進行的，該操作使得信號在稀疏域進行了非周期性的搬移，從而使能量泄露能近似均勻的分布在整個稀疏變換域中，在恢復重建的過程中，能以更高的精度求解出相應的散射系數。改進CLEAN算法抑制旁瓣過程是在循環中不斷的減去信號所對應的干擾，并逐步的求解出散射系數，在含有旁瓣串擾的條件下進行對應點擴展函數的消除，而這造成了改進CLEAN算法的誤差。因此壓縮感知就會比改進CLEAN算法精度要高。

3 仿真與結果

為驗證三維成像中改進CLEAN算法與壓縮感知的處理效果，用MATLAB在三維場景中建立理想的6個散射點，其散射系數和相對于場景中心的坐標如表1所示，仿真中頻率個數Nf為100，初始頻率f0為1.5 GHz步進頻率增量為10 MHz，橫向陣元和縱向陣元個數都為21個。場景中心與接收陣列相距2 m。

表1 不同目標的坐標位置和散射系數

基于閾值法提取散射中心，后向投影成像算法(back projection imaging algorithm，BP)處理的圖像、改進CELAN算法處理的圖像分別如圖2(a)、圖2(b)通過壓縮感知對散射系數的恢復如圖2(c)所示。

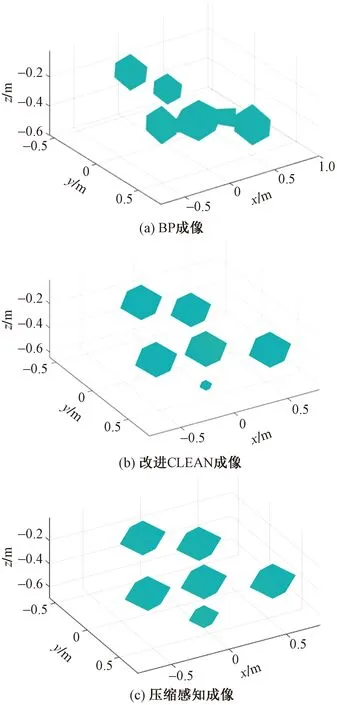
圖2 基于不同算法對散射系數的恢復圖像

可以看出，經過壓縮感知算法和改進CLEAN算法對散射系數的回復效果較好，使得小散射點也能夠分辨出來。

表2為改進CLEAN與壓縮感知對散射系數的恢復誤差。由下表可以看出壓縮感知方法恢復的散射點精度相對于改進CLEAN算法來說有大大提升。

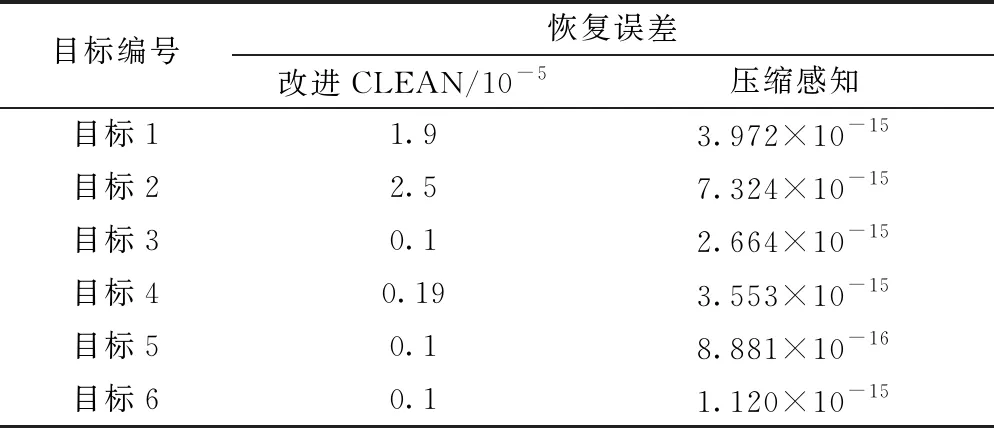
表2 不同算法對各個目標的恢復誤差

通過FEKO仿真驗證改進CLEAN算法和壓縮感知算法對RCS反演的影響，并與傳統的BP成像算法進行比較。用FEKO對如圖3(a)所示的飛機模型進行求解。將3種算法所反演的RCS與參考值進行比較，具體仿真如下。

基于傳統BP算法、改進CLEAN算法及壓縮感知的飛機模型成像分別如圖3(b)、圖3(c)、圖3(d)所示。

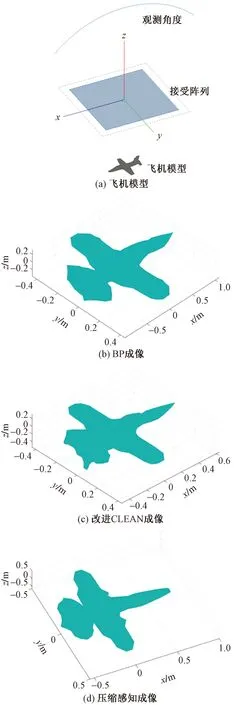
圖3 飛機模型基于不同算法成像

中頻處分別基于水平方位向x、垂直方位向y以及觀測角度為零度時不同頻率的RCS值，如圖4所示。

圖4 x、y向觀測角度及觀測角度為零度時不同頻率的RCS

由圖4可以看出，基于壓縮感知成像的RCS反演，其效果更加接近參考值。由于BP成像存在旁瓣效應，因此距離(z軸)方向的散射系數會相互串擾，其反演的RCS在不同的頻率中有較大的誤差。為便于觀察3種方法與參考值的不同，如表3所示。

基于CS細分網格三維成像的RCS測量的采樣間隔為(0.07 m，0.07 m, 0.07 m)。由表3可以看出，壓縮感知細分網格成像所反演的RCS優于傳統成像，針對飛機模型，在機尾處中間豎立的機翼，散射點較難提取，反演的角度RCS也會有誤差。整體來看，基于壓縮感知細分網格成像的RCS測量精度更高。尤其在距離向顯著提升了不同頻率的RCS反演精度。

表3 不同算法對飛機RCS的均值差與標準差

4 結論

基于旁瓣抑制的三維成像RCS測量技術展開了具體研究，先詳細介紹了合成孔徑的三維成像模型，并給出了成像RCS反演的主要步驟。分析了基于成像算法產生旁瓣的原因；其次介紹了基于改進CLEAN算法以及壓縮感知兩種方法對成像旁瓣的抑制；最后基于不同算法對目標RCS反演進行仿真驗證得出以下結論。

(1)改進CLEAN算法與壓縮感知算法抑制旁瓣的原理都是消卷積的過程，目標RCS反演時，兩者都會降低有限截斷誤差帶來的效應。

(2)改進CLEAN算法與壓縮感知算法都有效的抑制了圖像的旁瓣，提高了RCS的測量精度。而基于細分網格的壓縮感知有著相比于改進CLEAN算法更好的優勢。該方式直接從信號入手，不需要額外成像或部分成像，該方式可以以遠低于奈奎斯特的采樣率對回波進行稀疏采樣，當滿足重構條件時，即可穩定而高精度地完成對目標像的稀疏重構，這對散射系數的精確提取和RCS的精確反演提供了有利的條件。