散體介質SHPB 被動圍壓試驗體應力計算的理論修正方法*

陳昊祥，李 杰，鄧樹新，王德榮，王明洋,

（1. 北京建筑大學土木與交通工程學院, 北京 100044；2. 陸軍工程大學爆炸沖擊防災減災國家重點實驗室, 江蘇 南京 210007；3. 南京理工大學機械工程學院, 江蘇 南京 210094）

散體介質作為消波耗能材料廣泛地應用于土木工程以及軍事工程等領域，其在高應變率下的動態物理力學性質對于研究爆炸沖擊荷載作用下結構的防災減災問題具有重要意義。然而，關于中高應變率（10～10s）下散體材料是否具有應變率效應，現有研究尚存在嚴重分歧。Yamamuro 等發現干砂的應力-應變曲線在不同應變率（10～10s）下存在明顯差別，具有顯著的應變率效應。Luo 等的試驗結果卻顯示，不同應變率下散體材料的應力-應變曲線基本相同，未發現明顯的應變率效應。造成上述差異的原因可能在于，約束條件選取的不同，具體原因尚有待進一步研究。而且，隨著我國南部海域島礁建設的蓬勃發展，散體介質中-高應變率下的動態力學性質研究的應用前景越來越廣闊。

分離式霍普金森壓桿（split Hopkinson pressure bar, SHPB）是研究材料中-高應變率下動態力學性質的重要試驗手段。相較于固體材料，散體介質SHPB 試驗過程中需要使用剛性套筒固定散體材料試樣。通過測量套筒外壁的環向應變，根據厚壁圓筒理論（平面應力狀態）即可反推出散體介質試樣中的應力與變形場。需要指出的是，散體材料的波阻抗較低，為了保證整個試驗過程中試樣內部的應力平衡，試樣的長度通常較短（一般不超過10 mm）。由于套筒的約束使得散體介質試樣邊緣處產生了顯著的端部效應（如圖1 所示），此時套筒不能滿足平面應力假設，因此文獻[2-3, 9]中得到的結果并不準確，需要進行修正。魏久淇等指出上述文獻中計算存在的缺陷，嘗試通過數值模擬手段進行修正并與試驗結果對比，驗證了數值修正方法的正確性，但受限于數值模擬方法自身的缺陷，他們未能給出修正系數的無量綱形式，導致數值修正方法的適用范圍有限。

圖1 鋼套筒端部效應的示意圖Fig. 1 The configuration for the edge effect in the steel sleeve

受魏久淇等研究的啟發，本文中借助經典板殼理論，將剛性套筒簡化為受均勻帶狀內壓作用的圓柱形殼體，推導套筒徑向位移、環向應變與帶狀內壓及套筒幾何、力學參數的關系，得到套筒徑向位移、環向應變沿其軸向的分布；分析套筒長度、厚度、內外徑以及帶狀內壓寬度之間等無量綱幾何參數對計算結果的影響；將理論計算結果與試驗結果和數值模擬結果進行對比，驗證理論計算的正確性。

1 厚壁圓筒理論計算試樣中的應力場

為了探究聚合物材料在大變形條件下的非彈性力學行為，Ma 等采用厚壁圓筒理論對試樣中的應力場進行了估算，后續的散體介質SHPB 被動圍壓試驗研究大多采用了相同的計算方法。

假設散體試樣與套筒之間的徑向應力滿足連續性條件，在極坐標下，試樣內部的應力和變形分別為：

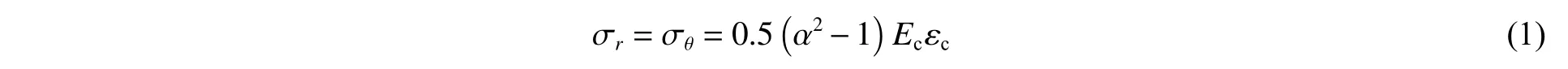
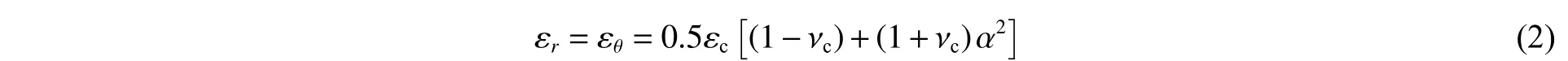
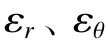
由式(1)～(2)可知，試樣的靜水壓力 σ 和體積應變ε分別為：

考慮到試樣軸向應變 遠εε大于徑r向 和環ε向應變θ ， 即ε?ε=ε，于是試樣的體積應變可化簡為：

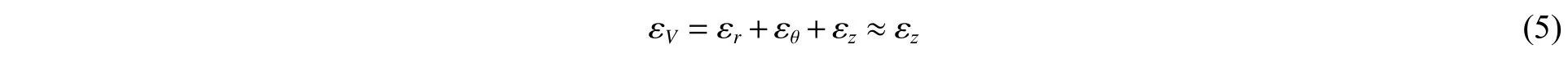
通過測量套筒外壁環向應變 ε，并結合式(1)～(5)，即可得到散體介質試樣的應力與變形狀態。需要注意的是，上述理論推導過程中假定套筒處于平面應力狀態，但由于端部效應的存在，套筒受力并不能簡化為平面應力問題，因此計算需要修正。

2 圓柱殼體理論計算試樣中的應力場

為了便于環向應變 ε的量測以及試件裝樣，在進行散體介質SHPB 試驗時通常選用壁厚較薄的剛性套筒。試驗過程中試樣內部始終處于應力平衡狀態，因此可將試樣與套筒間的相互作用力按靜力處理。此時，套筒可簡化為受均勻帶狀內壓作用的圓柱形殼體，如圖2 所示。圖2中，套筒長度為2，均勻內壓強度()作用長度為2，取極坐標(,,)。

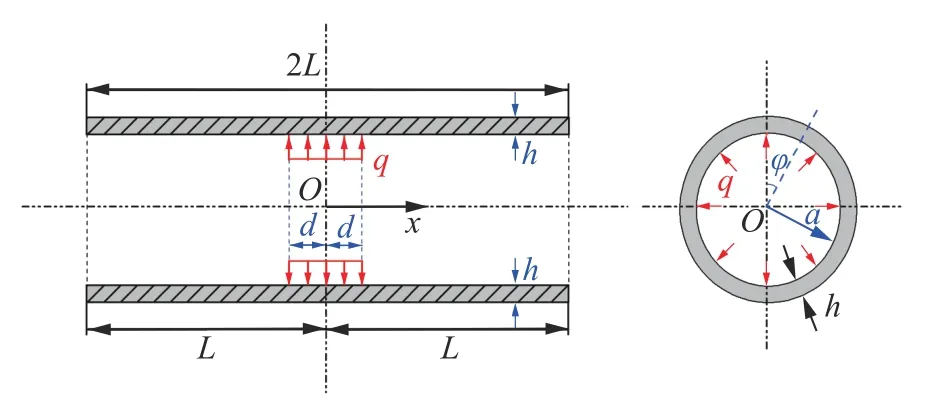
圖2 套筒受力Fig. 2 Stress on the steel sleeve

由經典彈性板殼理論可知，忽略軸向變形，均勻內壓作用下套筒的平衡方程為：

對均勻內壓()進行Fourier 級數展開，可得：

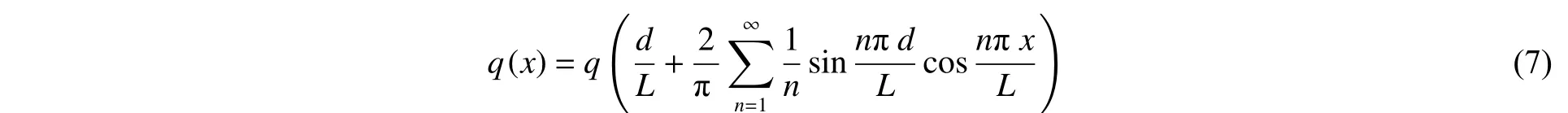
將式(6)對坐標進行Fourier 變換并化簡，可得：

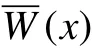
對式(8)進行Fourier 逆變化，可得套筒徑向位移函數()：

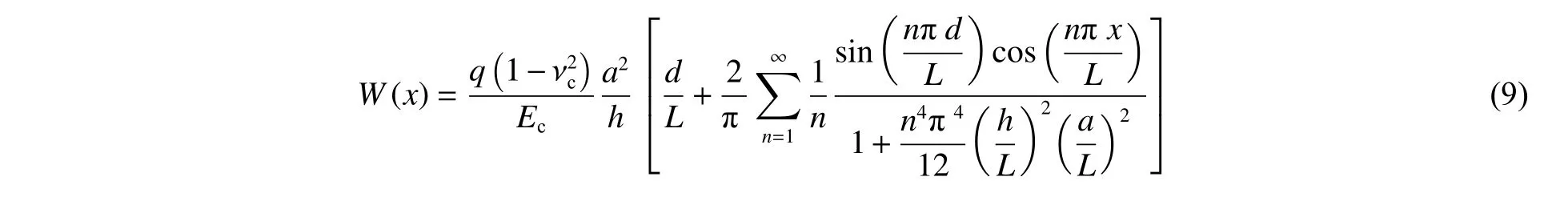
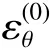
3 數值模擬與理論對比

為了驗證本文計算模型的正確性，采用文獻[4]中試驗參數并與其數值模擬結果進行對比，數值模擬過程中參數選取為：套筒長度2=94 mm，套筒厚度=4.95 mm，套筒內半徑=18.55 mm，套筒外半徑=23.5 mm，套筒彈性模量=210 GPa，泊松比ν=0.3；帶狀內壓寬度2=7, 8, 9, 10, 12, 15, 20, 30, 40, 50,60, 70, 80, 90, 94 mm。

將上述計算參數代入式(10)，可求得環向應變沿套筒長度方向的分布曲線，如圖3 所示。由圖3 發現，隨著內壓寬度的增大，環向應變的分布范圍擴大、幅值先增大后減小。當帶狀內壓寬度2=10 mm（散體介質試樣的長度極限）時，環向應變的分布范圍約為套筒長度的1/3，此時柱殼理論計算結果約為厚壁圓筒理論結果的0.5 倍，表明厚壁圓筒理論計算結果與實際變形相差較大；當2≈40 mm 時，柱殼理論計算結果達到最大值，約為厚壁圓筒理論結果的1.06 倍；當2=2時，柱殼退化為厚壁圓筒。

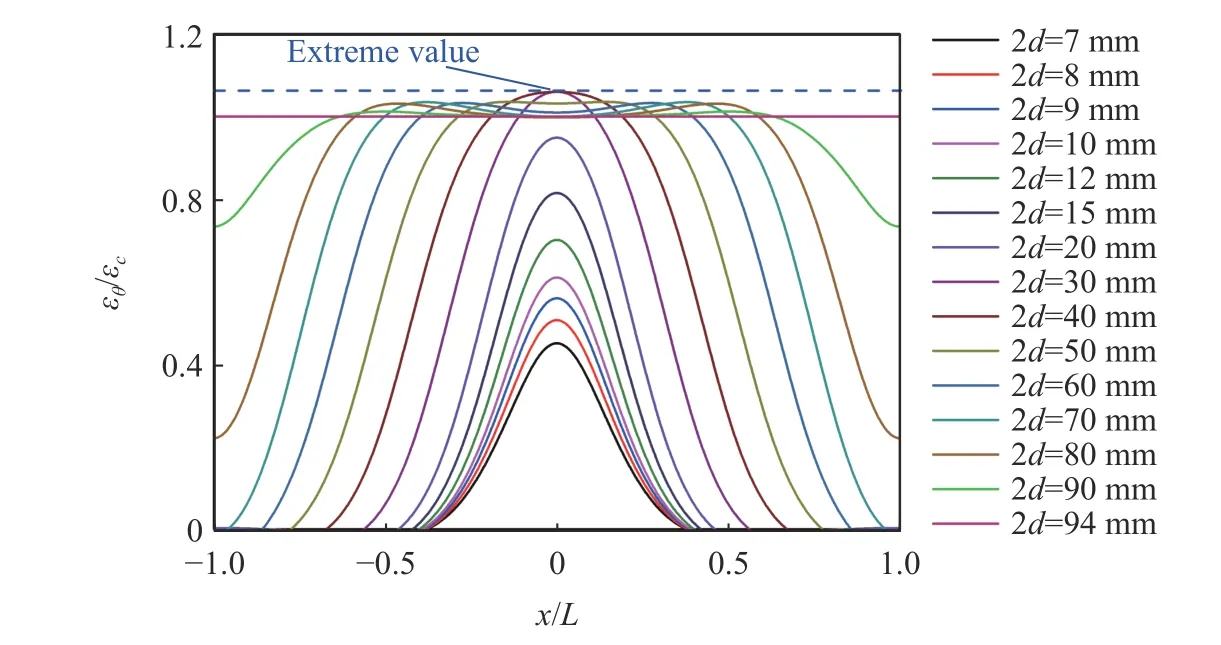
圖3 套筒環向應變沿軸線的分布Fig. 3 Distribution of hoop strain on the outer surface along with the steel sleeve

將文獻[4]中數值計算得到的修正系數與圓柱殼體理論計算結果進行對比，如圖4 所示。由圖4可知，當/≤0.25 時，殼體理論計算結果與數值計算結果基本重合，而與厚壁圓筒理論計算結果則相差較遠；當0.25＜/≤0.625 時，殼體理論計算結果略高于數值和厚壁圓筒理論計算結果，最大誤差為6%；當/＞0.625 時，理論計算結果和數值計算結果基本相同，此時2 種理論精度都可滿足試驗要求。

圖4 理論計算得到的修正系數與數值模擬結果的比較Fig. 4 Comparison of theoretical correction factors with numerical results

為了進一步驗證殼體理論計算結果的準確性，并分析套筒長度、內外徑以及均勻帶狀內壓寬度等幾何參數對計算結果的影響，本文中在文獻[4]中數值計算的基礎上，利用Abaqus/Explicit 有限元模擬軟件進行補充計算，模型網格采用六面體線性縮減積分單元，邊界條件為自由邊界，不同計算模型網格劃分示意圖如圖5 所示。

圖5 模型網格劃分Fig. 5 The element meshes for the numerical models

算例1：套筒長度2=94 mm，套筒厚度=3 mm，套筒內半徑=19 mm，套筒外半徑=22 mm，套筒彈性模量=210 GPa，泊松比ν=0.3；帶狀內壓寬度2=7, 8, 9, 10, 12, 15, 20, 30, 40, 50, 60, 70, 80, 90,94 mm。此時，理論計算與數值計算對比結果如圖6 所示。

算例2：套筒長度2=50 mm，套筒厚度=4.95 mm，套筒內半徑=18.55 mm，套筒外半徑=23.5 mm，套筒彈性模量=210 GPa，泊松比ν=0.3；帶狀內壓寬度2=7, 8, 9, 10, 12, 15, 20, 30, 40, 50 mm。此時，理論計算與數值計算對比結果如圖7 所示。

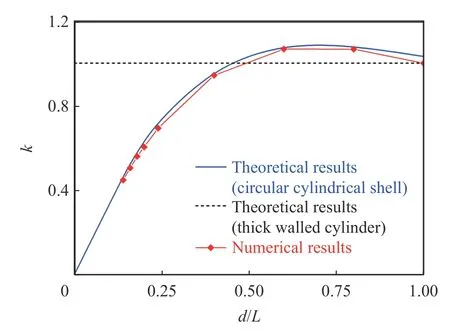
圖7 理論計算得到的修正系數與數值模擬結果的比較（算例2）Fig. 7 Comparison of theoretical correction factors with numerical results (case 2)

對比圖6～7 中理論與數值計算結果可以發現，隨著無量綱參數/、/、/的改變，殼體理論的計算結果與數值計算結果非常接近，且精度遠高于厚壁圓筒理論。

圖6 理論計算得到的修正系數與數值模擬結果的比較（算例1）Fig. 6 Comparison of theoretical correction factors with numerical results (case 1)

4 試驗與理論對比

為了進一步驗證殼體理論的準確性，將理論計算與試驗結果進行對比，試驗結果同樣采用文獻[4]中的數據，具體如圖8 所示。根據試驗數據計算可知，含水質量分數ω 為25%和30%的鈣質砂試樣SHPB 試驗對應的飽和點（飽和度S= 1）分別為ε=0.221 2 和ε=0.157 4。當軸向應變ε超越飽和點之后，水壓力將占據主導地位，此時散體試樣處于靜水壓力狀態，即σ=σ=σ。

觀察圖8 可以發現，當軸向應變在飽和點之前，理論計算的徑向應力σ明顯小于軸向應力σ試驗值，這是由散體介質的側向壓力系數λ 通常小于1 引起的。根據試驗和理論數據進行估算，可知λ≈0.548；當軸向應變超過飽和點之后，殼體理論（式(10)）計算得到的徑向應力σ與軸向應力σ的試驗值基本重合，驗證了殼體理論的準確性。而厚壁圓筒理論（式(1)）的計算結果則明顯低于試驗值，表明厚壁圓筒理論的計算誤差很大，此時并不適用。

圖8 理論軸向應力-應變理論曲線與試驗結果[4]的比較Fig. 8 Comparison of theoretical axial stress-stain curves with experimental results[4]

5 結 束 語

SHPB 被動圍壓試驗為探究散體介質在爆炸和沖擊荷載作用下的力學行為提供了一個行之有效的方法。本文中針對相關試驗設計和計算中存在的弊端和不足，借助經典板殼理論對現有計算方法進行修正，總結如下。

(1)將SHPB 被動圍壓試驗中用于約束散體介質的剛性套筒簡化為受均勻帶狀內壓作用的圓柱形殼體。推導了套筒徑向位移、環向應變與均勻帶狀內壓及套筒幾何、力學參數的定量關系，得到了套筒徑向位移、環向應變沿其軸向的分布。

(2)分析了套筒長度、厚度、內外徑以及均勻帶狀內壓寬度之間等無量綱幾何參數對計算結果的影響，并與數值計算結果進行對比，驗證了修正系數的準確性。

(3)將理論結果與試驗和數值模擬結果進行對比分析，驗證了理論計算的正確性。