基于一題多解 發展科學思維
——以第38屆物理競賽預賽第13題為例
呂艷坤 盧 杰 魏 森
(1.東北師范大學教育學部,吉林 長春 130024;2.鄭州實驗外國語中學,河南 鄭州 450052;3.東北師范大學附屬中學,吉林 長春 130024)
一題多解是物理教學中常用的教學手段,旨在通過對于方法合理性的判斷、對于方法便捷性的對比、對于方法適用性的反思來拓寬解題思路,進而提高學生的科學思維能力.[1]本文以第38屆全國中學生物理競賽預賽第13題為例,探尋指向學生科學思維發展的習題教學策略.
1 原題再現
6個小朋友在操場上玩追逐游戲.開始時,6個小朋友兩兩間的距離相等,構成一正六邊形.然后每個小朋友均以不變的速率v追趕前面的小朋友(即小朋友A追B、B追C、C追D、D追E、E追F、F追A),在此過程中,每個小朋友的運動方向總是指向其前方的小朋友.已知某一時刻t0=0,相鄰兩個小朋友的距離為l,如圖1所示.試問:
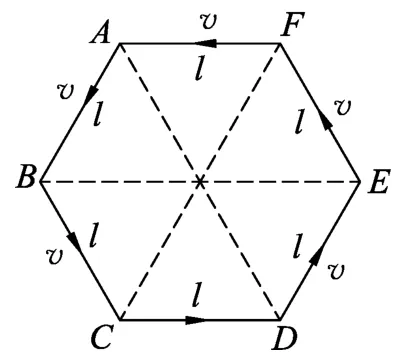
圖1
(1)從t0時刻開始,又經過多長時間后面的小朋友可追到前面的小朋友?
(2)從t0時刻開始,直至追上前面的小朋友,每個小朋友又跑了多少路程?
(3)在t0時刻,每個小朋友的加速度大小是多少?
2 試題分析
本題為物理競賽中典型的曲線追及問題,與之類似的還有獵犬追狐貍(狐貍沿直線,獵犬沿曲線)和獵犬追狼(狼沿圓周,獵犬沿曲線).其共同點是追及者速度大小不變,速度方向始終指向被追擊者且時刻發生在變化,需要從時間和二維空間同時來考慮相遇.
2.1 標準答案解析
由對稱性知,每個小朋友運動情況是一樣的,以小朋友A為例.
(1)在從小朋友A到小朋友的B連線方向上,小朋友A相對于B的速度分量為
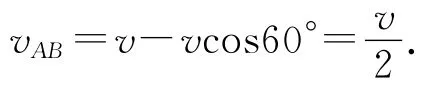
小朋友A追上B的時間為

(2)從t0時刻開始,直至追上前面的小朋友,每個小朋友所跑的路程為
s=vt=2l.
如圖2所示,設經d t時間小朋友A運動到A′點,小朋友B運動到B′點,小朋友A的速度方向變為從A′點指向B′點,轉過的角度為dθ.由余弦定理得
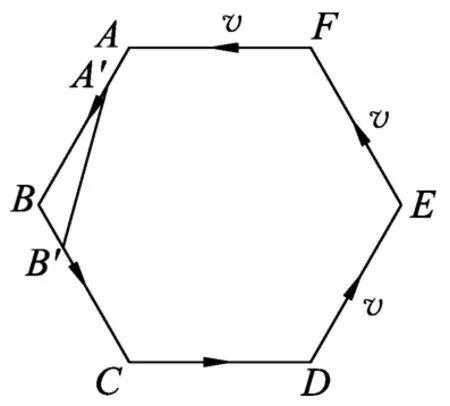
圖2
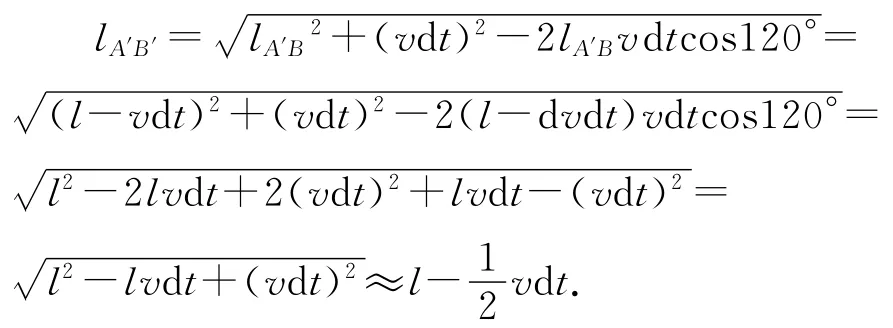
由正弦定理得
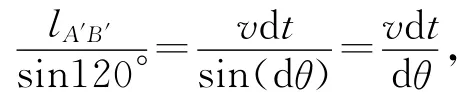
式中dθ為△A′BB′中兩邊lA′B與lA′B′之間的夾角.
小朋友A運動的角速度為
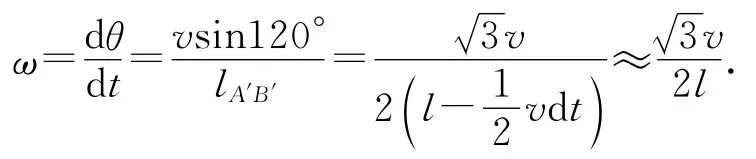
小朋友A運動的法向加速度為
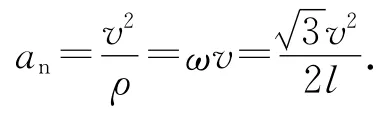
則小朋友A的加速度大小為
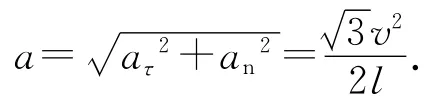
2.2 標準答案評析

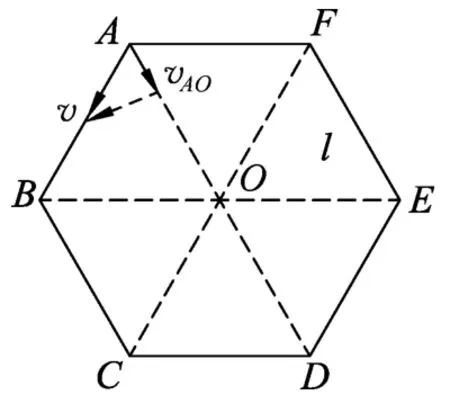
圖3
第(2)問,求運動路程.可由s=vt求得,一旦第(1)問追及時間確定,路程也隨即求得,因此本文不再贅述.
第(3)問,求加速度大小.標準答案采用的是自然坐標系下分別求小朋友的切向加速度和法向加速度.在法向加速度計算過程中首先采用微元思想構建一個三角形,在三角形中利用余弦定理和正弦定理求得小朋友在初始時刻的角速度,進而得到法向加速度和實際(合)加速度.微元思想是基于宏觀事物的普遍性(共性)不僅存在于事物發展的全過程中,而且也包含在微元的特殊性(個性)這一基本屬性的基礎上,而產生的一種創造性思維方式,往往能起到化曲為直、化難為易、化繁為簡的功效.[2]自然坐標系的運用,看似直觀,但是實際計算過程較為繁瑣,還需要用到正弦定理和余弦定理等數學知識,對學生跨學科能力要求較高.
縱觀整個標準答案解析過程,雖然涉及的方法多樣,但是存在一定不足:(1)解題方法跳躍較大,缺乏整體的連貫性;(2)方法與方法之間缺乏整合,遷移性有限,易引發學生的思維混亂;(3)總體計算量過大,未體現出物理學科的清晰、簡潔之美.
3 多解賞析
為了激發學生學習興趣,培養學生科學思維,彰顯物理邏輯的科學、嚴謹與連貫,本文采用微積分和極坐標方法,分別從微觀和宏觀兩個角度進行多解賞析.
3.1 微積分方法
設在很短一段時間d t之后,6個小朋友分別到達新的位置,如圖4所示,過D′做CD所在線段的垂線D′P,則在△C′D′P 中滿足勾股定理
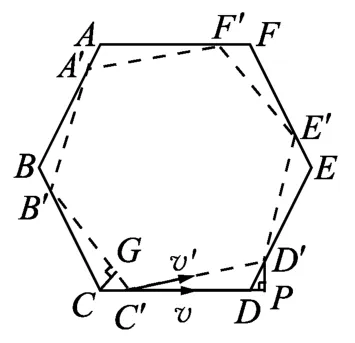
圖4
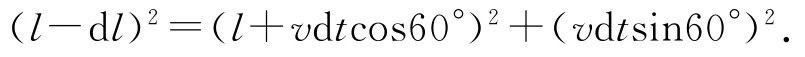
展開后可得
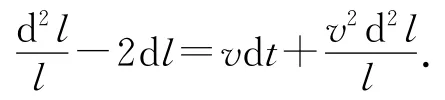
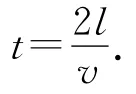
如圖4所示,過C點作B′C′邊的垂線CG,由于頂角很小,則△B′CG近似為等腰三角形.速度偏轉角和位移偏轉角相等,速度矢量三角形是一個頂角很小的等腰三角形,則△B′CG和速度矢量三角形相似,易得
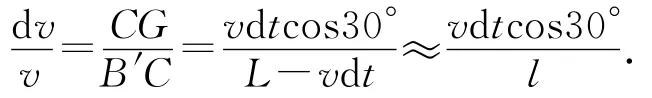
變形可得
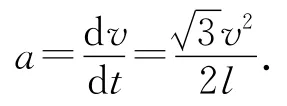
評析:自牛頓和萊布尼茲提出微積分以來,微積分就與物理學的發展密不可分.但是考慮到高中生認知水平和數學基礎,高中物理有意避開了使用微積分,物理競賽對微積分也不作要求.近年來由于競賽難度的加大,對數學能力要求進一步提高,微積分作為高等數學的基礎已成為物理競賽學習的必備知識.從微積分入手解決競賽問題,有助于學生從微觀層面認識事物變化的本質,從時間與空間融合的雙重視角分析事物變化的規律.
3.2 極坐標方法
如圖5所示,以中心O為原點建立平面極坐標系,以小朋友E為研究對象,由題意得

圖5
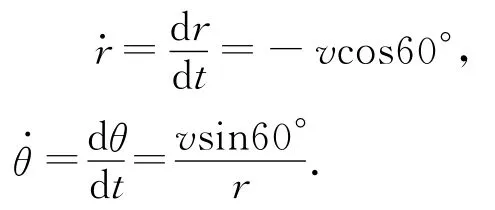
對時間積分可得極徑r關于時間的表達式為
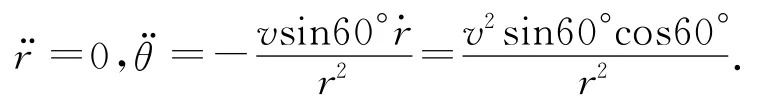
根據極坐標加速度公式
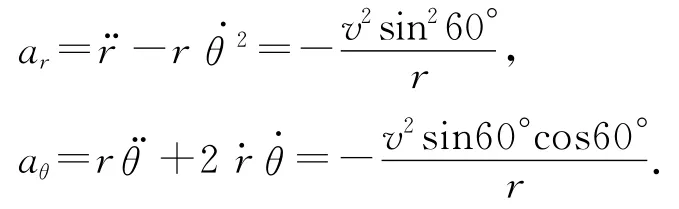
初始時刻,r=l,由a=arer+aθeθ且er⊥eθ可得
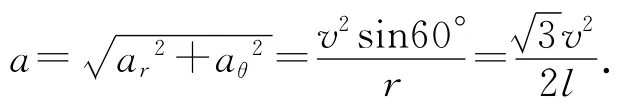
評析:笛卡爾坐標系、自然坐標系和平面極坐標系是解決平面物理問題最常見的3種坐標系.對于此類型追擊非常規的直線或圓錐曲線運動問題,笛卡爾坐標系會使計算過程變得極為繁瑣,不宜采用;自然坐標系在標準答案里已有使用,故不再贅述.平面極坐標系雖然是復賽和決賽考試內容,但是在涉及平面曲線運動過程(尤其是有心運動)時,選取平面內一點為參照原點,在規定極軸后以極徑和極角來描述物體的空間位置,將復雜的物理運動過程轉化為簡潔的數學公式,在對物體進行運動分析時極為方便.[3]3種坐標系的對比分析,有助于學生深化對于坐標系的適用范圍和優劣勢的理解,對于其后續學習提供基礎性支撐.

