基于正交異性橋面板應力監測數據的車輛荷載識別

王超， 周卓升， 賀偉誠， 楊青祥

(湖北工業大學土木建筑與環境學院， 武漢 430068)

隨著社會飛速發展，交通流量急劇增長，流量超限、超載現象時有發生，大量車輛荷載作用會引起橋梁結構的疲勞損傷累積甚至坍塌破壞，因此獲取車輛荷載信息是橋梁監測系統的重要內容，對結構的性能評估與維修養護具有重大工程意義[1-2]。

車輛荷載的動態監測主要分為基于動力響應的荷載識別、基于路面式動態稱重和非路面式動態稱重。基于動力響應的荷載識別通過車-橋耦合系統振動方程求解任意時刻車輛和橋梁接觸處相互作用力來識別車輛荷載。文獻[3-9]在這方面開展了大量研究工作，這類方法受路面不平整度、車輛速度等因素影響大，需要的系統參數多，計算復雜、不確定因素多。路面式動態稱重通過在路面頂部或路面埋入傳感器來監測車輛軸重、軸距、車速等信息，但是它只能監測車輪短時的動壓力，與靜態軸重存在一定偏差，而且需要開挖路面，影響交通[10]。非路面式動態稱重是在橋梁不同截面底部布設傳感器，采集車輛通過時的完整動態響應來識別荷載信息，如基于動應變的橋梁動態稱重系統(bridge weigh-in-motion, B-WIM)，具有監測數據時間長，精度高，安裝維修方便、不中斷交通、不破壞路面、造價低等特點[11]。Ojio等[12]提出了不同小車行駛過橋梁時的應變響應與小車順橋向加載位置的面積之比等于車輛總重面積之比。Chen等[13]研究了大跨連續鋼桁架橋結構的應變響應面積與軸重的對應關系來識別車輛總重。目前的B-WIN研究多是針對簡支梁橋、板橋、鋼梁橋和桁架橋結構，針對正交異性橋面板結構較少[14]。

Dempsey等[15]利用有限元模擬正交異性橋面板頂板跨中U肋的理論影響線，基于Moses算法，利用理論影響線計算車輛軸重。馬鵬飛等[16]利用車輛輪載作用在不同橫向位置時U肋之間的應變變化的規律來識別軸重。正交異性橋面板局部受力明顯、影響線短，非常合適采用B-WIN技術識別車輛荷載。許多橋梁建立了健康監測系統，研究利用監測系統應力測點實現車輛荷載的識別，具有較大的經濟效益。

基于動應變的B-WIN車輛荷載識別的關鍵是確定車輛作用的橫向位置及荷載的標定，針對這兩個問題，研究基于正交異性橋面板應力監測數據的車輛荷載識別技術，提出了基于余弦相似度這一指標來定位車輛荷載的橫向位置，探討了荷載標定間距對車重總重識別的影響，通過數值模擬和模型試驗驗證所提出的方法。

1 荷載識別方法

正交異性鋼橋面板承受車輪荷載直接作用，結構應力以局部效應為主。在橫隔板支撐下，U肋受力類似連續梁受力，其應力影響線很短。車輛荷載通過橋面板時，車輛荷載總重與U肋的應力響應的總面積和荷載橫向作用位置有關，為此首先要識別車輛荷載通過時的速度和橫向位置。

1.1 車速的識別

為便于說明，這里選取一個正交異性橋面板節段模型，如圖1所示。在相鄰節段跨中(圖1中B-B和C-C截面)同一U肋下緣分別布設了測點N7和N8。已知測點N7和N8間距為d，假定車輛勻速通過橋面，測點N7和N8測得的應力響應分別為P7(t)和P8(t)，采樣頻率為fs。由于測點受力具有局部性，兩個測點的應力響應具有相似性，對兩測點響應求互相關函數，如圖2所示。

A-A、B-B、C-C、D-D為截面；N1～N8為測點編號

圖2 測點N7和N8的互相關函數

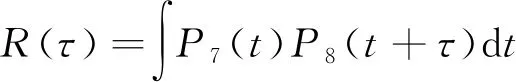
(1)

式(1)中：R(τ)為測點N7和N8響應的互相關函數；t為時間；τ為時移，R(τ)的極值對應的τmax即為車輛通過兩測點的時間差，隨后可以通過式(2)估計車速。

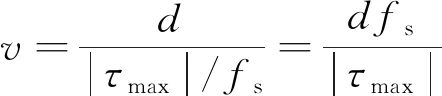
(2)

1.2 橫向位置識別

如圖1所示，在一個車道內多個U肋下緣分別布設應力測點，實際測點數量隨車道寬度和U肋尺寸而變，不失一般性，這里布設了6個應力測點N1～N6。當車輛在橫向不同位置從正交異性橋面板上駛過時，采集所有測點的應力響應時程。利用估計的車速分別計算每個測點應力響應的面積。

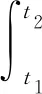
(3)

式(3)中：Pij為車輛在橫向位置為i處j測點的應力響應；Sij為應力響應Pij的響應面積；t1為車輛第一個軸行駛至應力影響線起始零點(如圖1A-A截面處，實際影響線起始零點會更長，但是超出A-A截面外影響線很小，對識別結果影響很小，這里近似用A-A截面表示)的時刻；t2為車輛最后一個軸行駛至應力影響線起始零點(如圖1D-D截面處)的時刻。

對于確定車輛作用位置i，所有測點應力響應面積構成向量Ai=[Si1,Si2,…,Si6]，當車輛橫向作用在不同位置時，應力響應面積向量Ai將發生改變。首先對車輛作用在橫向不同位置時的應力響應面積向量進行實測標定得到標準值AB=[A1,A2,…,Ai]，然后將荷載橫向位置未知時的實測應力響應面積向量AT=[AT1,AT2,…,ATj]分別與標準值AB進行比較，這里引入余弦相似度指標CI來估計橫向位置，可表示為

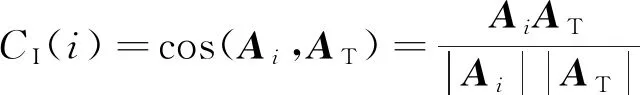
(4)

CI越接近1，表明Ai、AT這兩個向量越相似，找到AT的CI指標最接近于1時的向量Ai，則可以估計荷載橫向作用于標準值Ai對應的位置。

1.3 車重識別

設有一m個車軸的車輛在橫向位置i以速度v駛過橋梁，測點j的應力響應為

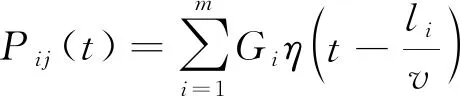
(5)

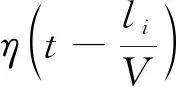
該測點的應力響應面積為

(6)

由于各軸單位荷載應力影響線的面積相等可得

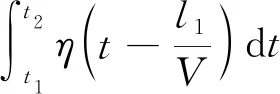
(7)

式(7)中：1≤i≤m。

則車輛的荷載總重Gtotal可表示為

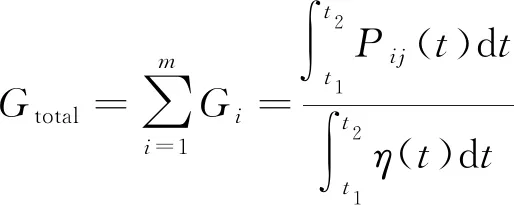
(8)

可見，車輛總重只與測點的應力響應面積和單位荷載應力響應面積有關，與軸數和軸距無關。

實際荷載識別前，需要將荷載總重為Gcali的小車從橫向不同位置通過橋梁時的應力響應面積作為標定數據，然后估計待測車輛橫向位置，車輛荷載總重則可以采用式(9)識別。

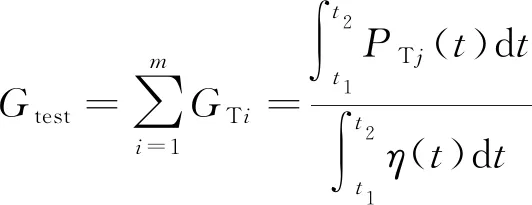
(9)

式(9)中：Gtest為待測車輛總重；GTi為待測車輛的第i軸軸重；PTj(t)為待測車輛在測點j處的應力響應。

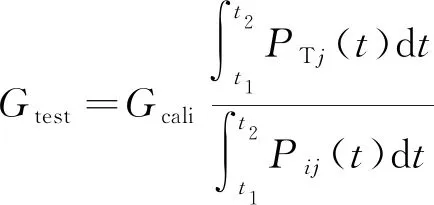
(10)

因此可以通過單個測點可以識別車輛荷載總重，考慮到噪聲干擾，可取兩個應力響應面積最大的測點來識別荷載然后取均值。

2 數值模擬

為了驗證所提方法，進行數值模擬分析。模型尺寸參考某實際正交異性鋼箱梁主梁，橫橋向取2個行車道寬度共計7.5 m，順橋向取三跨橫隔板共計9.6 m。面板、U肋和橫隔板厚度分別為14、12、8 mm，均采用板單元模擬。不失一般性，這里主要對車輛位于中間車道時進行荷載識別，因此將中間車道內各構件加密劃分單元，尺寸為2 cm，其他部分單位尺寸為4 cm。面板在橫隔板支撐下受力類似于連續梁，這里將橫隔板的底部順橋向、橫橋向和豎向全約束，有限元模型如圖3所示。

圖3 有限元模型

首先計算單位軸荷載通過橋面的影響線，基于線性疊加原理計算實際多軸車輛通過橋面時測點的應力響應。這里未考慮動力影響，動力作用會影響實際應力數值大小，但還是可以采用同樣的識別方法。

采用車輪作用面積為0.2 m(寬)×0.6 m(長)，輪距為1.8 m的單軸荷載沿著順橋向方向以0.2 m為一個作用點移動來模擬計算單軸荷載的應力影響線。車輛橫向位置以車道中心線處定義為x=0 cm。通過計算一個兩軸車(軸重為14 kN，軸距為2.7 m)從橫向不同位置通過橋面時的響應來標定測點應變響應面積，車輛橫向位置從-96～96 cm 每4 cm(定義為標定間距d)計算一次得到測點應力響應面積向量ABi。然后在相鄰位置間進行3次樣條插值到每1 cm一個值，得到標定的應力響應面積矩陣AB。

現取一總重21 kN，軸距為3.0 m的兩軸車作為待測荷載在橫向x=-42 cm處通過橋梁，計算其應變響應如圖4所示，為了考慮算法的抗噪性，分別對響應數據添加10%、20%的高斯白噪聲，這里噪聲大小定義為噪聲方差/信號方差)。橫向位置估計結果如圖5所示。

圖4 x=30 cm時N1～N6的應力響應

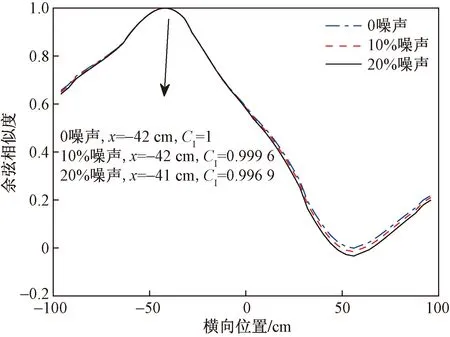
圖5 不同噪聲下的余弦相似度

可以看出，在各種噪聲情況下采用CI指標估計荷載橫向位置的誤差在1 cm以內。隨后根據無噪聲下估計的橫向位置識別出荷載總重為21.03 kN。采用同樣方法分別識別不同軸數和軸距的車輛荷載，識別結果如表1所示。

由表1可知：軸數、軸距對荷載橫向位置和荷載總重的識別無影響，這一點與式(8)相吻合；各種噪聲情況CI指標都可以很好定位車輛橫向位置，誤差保持在1 cm以內；無噪聲下總重識別誤差不超過0.11%，添加20%噪聲后荷載總重識別的最大誤差為3.07%，說明提出的方法具有較好的抗噪性能。

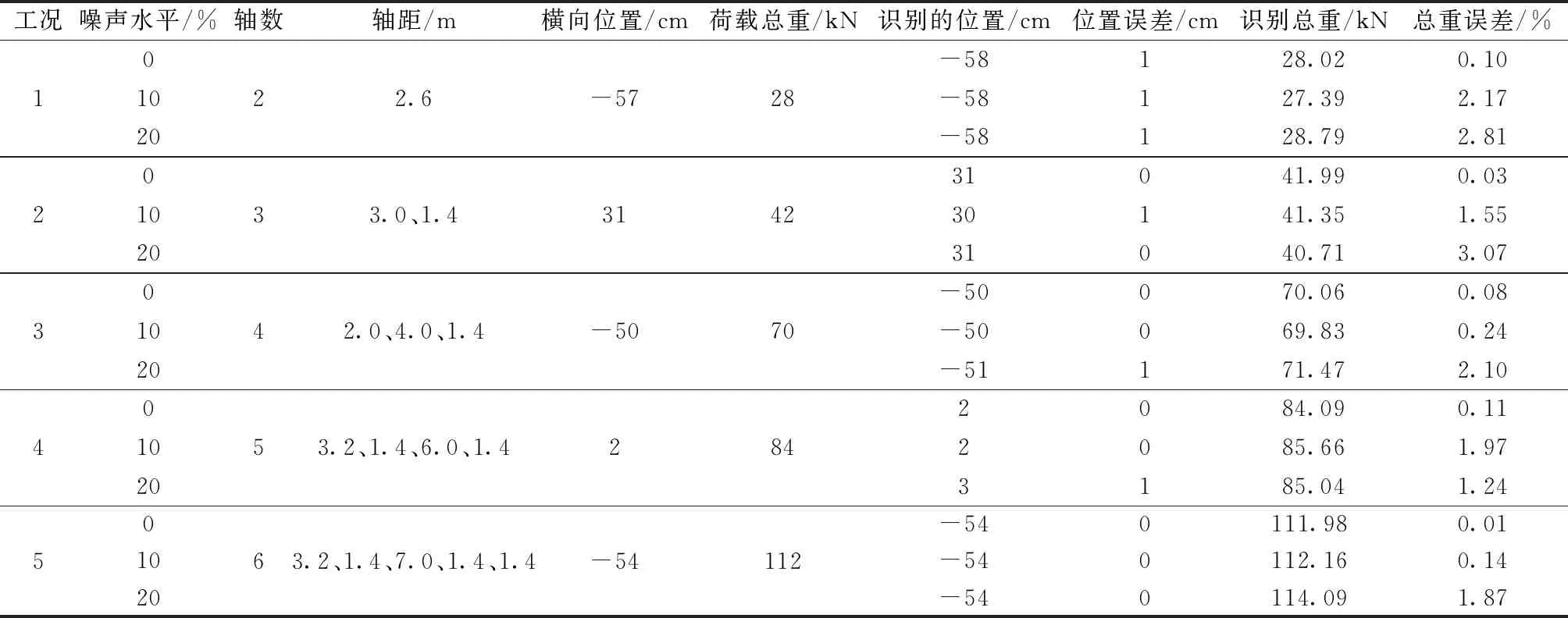
表1 不同車輛荷載橫向位置及總重識別結果

為了考慮荷載橫向標定間距d對識別結果的影響，這里分別按不同的間距提取上文計算的應力面積向量標定值ABi，然后進行三次樣條插值得到1 cm一個值得到應力面積矩陣標定值AB。取一個兩軸車在橫向位置x=-36 cm處通過橋面的數據進行荷載識別，識別結果如圖6所示。

圖6 不同標定間距下總重識別結果

可以看出,無噪聲下荷載總重誤差隨著標定點間距的增大整體上呈增大趨勢；噪聲比標定間距對車重識別誤差的影響更大；當標定點間距小于32 cm時，各種噪聲下的總重識別誤差不超過5%，標定間距大于32 cm時，各種噪聲下的總重識別誤差逐漸增大。因此，對荷載進行標定時，建議橫向標定間距不超過32 cm。

3 試驗模擬

3.1 試驗模型

為了進一步驗證提出的算法，設計了一個1∶6的縮尺模型試驗。模型長270 cm，寬83 cm，高20 cm，頂板下布設了6根U肋，6塊橫隔板，橫隔板間距為54 cm。設計了一個兩軸小車來模擬車輛荷載，小車尺寸為45 cm(長)×40 cm(寬)×28 cm(高)，軸距38 cm，輪距28 cm，輪寬2 cm，質量為22 kg，可在小車內添加質量塊改變軸重和總重。在中間節段(定義兩塊橫隔板中間部分橋面板為一個節段) U肋跨中下緣順橋向各布設1個應變計(N1～N6)，在相鄰節段跨中各布設1個應變計(N7和N8)。模型的詳細尺寸和測點布置如圖7所示。

圖7 模型及應變測點布置圖

在首尾兩塊橫隔板底端設置墊塊將鋼梁模型支撐起來。為保證試驗小車能勻速通過鋼梁，在鋼梁首尾各設置了一段引梁和尾梁，引梁和尾梁盡量貼近鋼梁，但跟鋼梁斷開以減小小車進出鋼梁時的振動。采用馬達牽引小車通過鋼梁，為保證小車平直的通過鋼梁，在小車上設置兩個限位孔，然后在鋼梁上方固定兩根平行鋼絲(鋼絲可以固定在橫向不同位置)，將鋼絲穿過小車上的限位孔，確保小車沿鋼絲方向移動。安裝好的試驗模型如圖8所示。

圖8 試驗模型圖

3.2 荷載標定

在小車內添加質量塊，實測小車總重為87.2 kg，定義小車處于鋼梁橫向中心處的位置為x=0 cm，采用馬達牽引小車在橫向39個不同位置(x=-21.5～16.5 cm)駛過鋼梁鋼梁，采集各測點的應變響應，采樣頻率為50 Hz。

車輛橫向作用位置x=-1.5 cm時，測點N1～N8的應變響應如圖9所示。對測點N7、N8的應力響應數據求互相關得到互相關函數曲線如圖10所示。

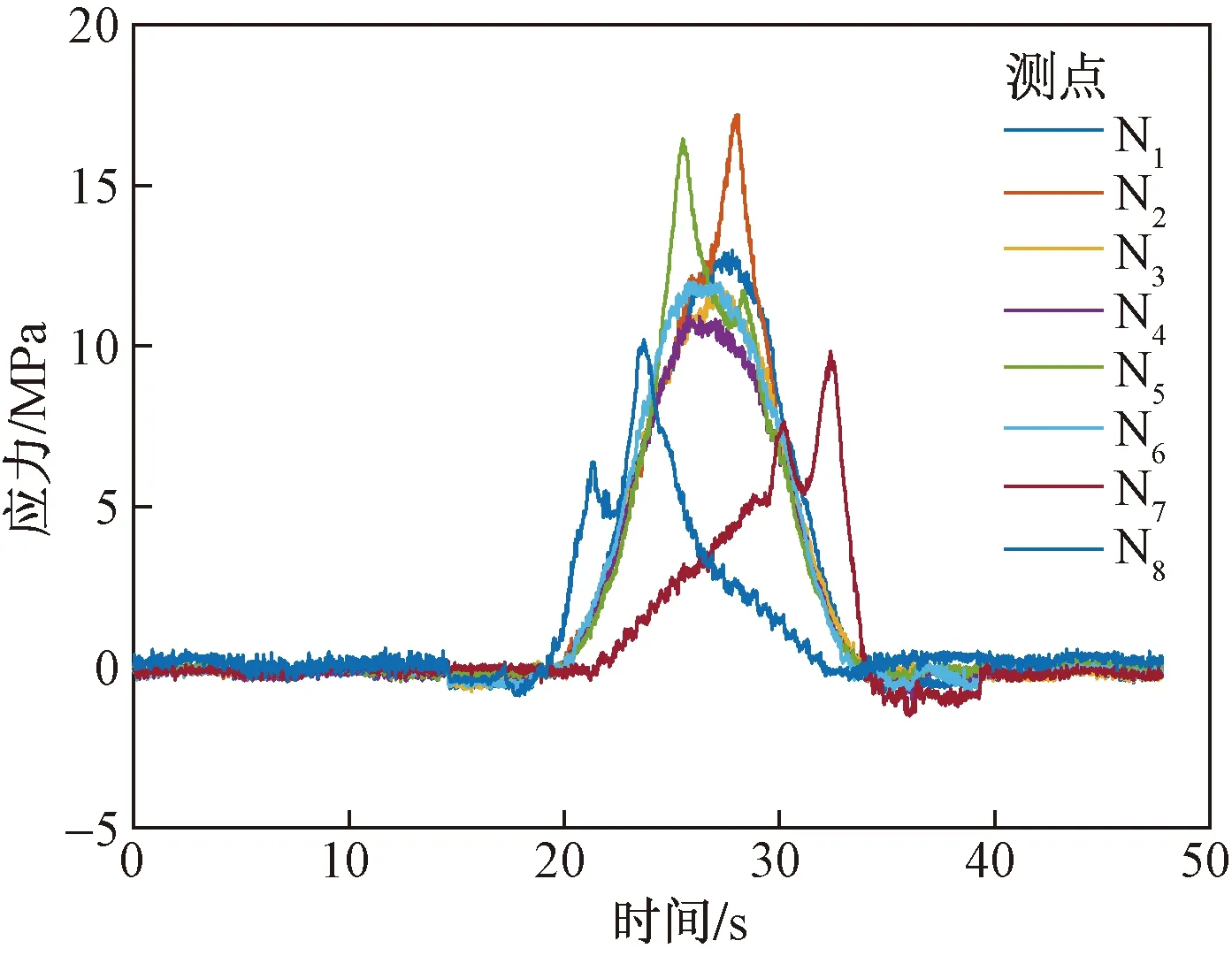
圖9 荷載位置x=-1.5 cm時，測點N1～N8的應力響應

圖10 測點N7、N8的互相關函數

通過搜索極值得到小車通過兩測點的時間差為8.96 s，由此可得到小車通過的時速為v=12.05 cm/s。

根據估計的車速計算測點N1～N6的應力響應面積為Ai=[Si1,Si2,…,Si6]。這樣就標定了一個橫向位置。采用同樣的方法可以標定所有其他位置對應的應力響應面積向量，得到間距為1 cm的標準應力響應面積向量AB=[A-21.5,A-20.5,…,A16.5]。

3.3 荷載識別

接下來將測試不同重量小車從不同橫向位置通過鋼梁模型時的響應，利用上述標定的結果來識別未知車輛荷載。根據小車重量和位置不同，共測試了4種情況，如表2所示。

以工況3為例，結構各測點響應如圖11所示。

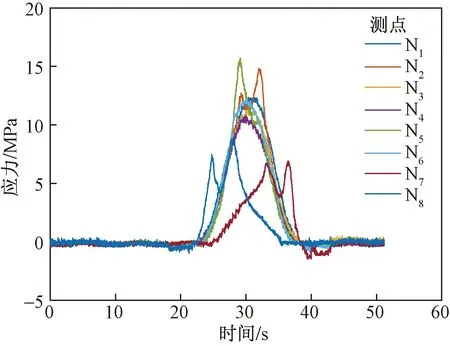
圖11 荷載位置x=1.5 cm時，測點N1～N8的應力響應

通過測點N7～N8的應力響應，識別得到小車速度為11.66 cm/s。再由測點N1～N6的應力響應計算得到應力面積向量AT=[13.449,13.545,13.132,12.023,12.713,14.034]，利用標定的應力響應面積向量AB計算CI指標，識別得到小車橫向位置x=0.5 cm，隨后識別小車荷載總重為100.61 kg。采用同樣的方法分別對其他工況進行荷載識別，結果如表2所示。

從識別結果(表2)可以看出，采用CI指標識別的橫向位置識別誤差在1 cm之內，荷載總重識別誤差最大為4.57%，表明所提方法可以有效準確地識別車輛荷載。

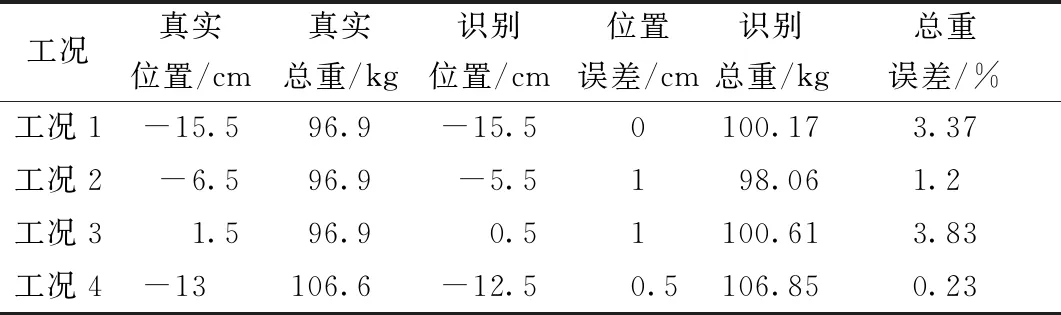
表2 不同工況荷載橫向位置及總重的識別

進一步研究了標定間距對荷載識別結果的影響，取小車在橫向位置x=2.5 cm處通過鋼梁的響應進行研究，結果如圖12所示。

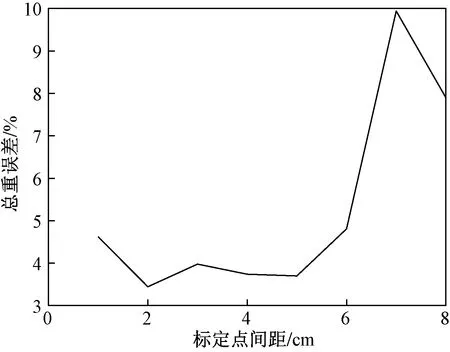
圖12 不同標定間距對車重識別結果的影響

可以看出，當標定點間距在5 cm以內時，荷載總重誤差不超過5%，超過5 cm以后，識別誤差迅速增大，考慮到試驗模型為1∶6縮尺模型，這一規律同數值模擬結果基本一致。

4 結論

正交異性橋面板局部受力明顯、影響線短、受結構自重影響小，非常合適采用B-WIN技術識別車輛荷載。論文研究了基于正交異性橋面板應力監測數據的車輛荷載識別技術。提出了基于余弦相似度這一指標來定位車輛荷載的橫向位置，研究探討了荷載標定間距對車重總重識別的影響。通過理論分析、數值模擬和模型試驗驗證提出算法的精確性和抗噪性能。得出如下結論。

(1)所提出的余弦相似度指標可以有效估計荷載作用的橫向位置。

(2)采用應變響應面積的方法可以準確識別車輛總重，算法具有較好的抗噪性能，識別結果不受車輛軸數和軸距的影響。

(3)在實際工程應用中，對荷載進行標定時，橫向標定間距建議不超過32 cm。

(4)提出的方法綜合利用橋梁健康監測系統應力測點實現車輛荷載的識別，相比昂貴的路面式動態稱重系統，具有較大的經濟效益。