低模量合成纖維對混凝土基本徐變的影響

李天倫，吳永根，吳豪祥

(1.空軍工程大學航空工程學院，西安，710038；2.中國人民解放軍94831部隊，福建武夷山，354300)

徐變是混凝土自身固有的性能，徐變會引起預應力混凝土結構的預應力損失、長期變形和內力重分布的顯著增加，對安全性和耐久性造成嚴重影響[1-2]，其自發現以來就引起了人們的高度重視。

在混凝土中摻入適量的纖維能夠很好地提升混凝土的使用性能，提高混凝土的強度，纖維混凝土作為一種新型復合材料已經廣泛應用于道路、橋梁、隧道和建筑等[3-4]。關于纖維混凝土徐變的研究最早主要針對鋼纖維，1989年Chern等對鋼纖維對混凝土徐變的影響進行了試驗，試驗結果表明，隨著纖維體積摻量的增加，徐變有所降低[5]。近年來，隨著高性能合成纖維混凝土的發展，徐變相關研究逐漸增多。于俊超等研究了鋼纖維和聚丙烯纖維混凝土的徐變特點，認為聚丙烯粗纖維只能改善混凝土的延性，無法抑制混凝土的徐變[6]。王玉清等測試了不同摻量聚乙烯醇纖維的混凝土徐變，測試數據表明，聚乙烯醇纖維體積含量在0.5%～2.0%范圍時，纖維混凝土的徐變均大于普通混凝土，且徐變隨纖維摻量的增大呈現兩頭大中間小的趨勢[7]。已有研究表明，高模量纖維對混凝土的橋接作用比較明顯，可以提高混凝土開裂后的韌性和抗沖擊性能，并已被證明能夠有效地減小混凝土的徐變[8]。目前已有較多模型可用于預測混凝土的徐變效應，如CEB-FIP模型[9]、GL-2000模型[10]、ACI-209模型[11]、GL-2000改進模型和B3模型[12]等。除此之外，Zhang則基于cox的剪滯理論，提出了在普通混凝土基本徐變基礎上乘以纖維填充因子作為纖維混凝土徐變的預測公式，但該表達式只適用于高模量纖維混凝土，并不能滿足低模量纖維混凝土[13]。雖然目前已有較多模型可對混凝土徐變進行預測，但由于各模型考慮因素不同，使上述模型之間存在較大區別，其對混凝土徐變計算適用性仍需進一步探討。

可以看出，針對合成纖維混凝土徐變的研究，目前還處于起始階段，試驗數據不夠充分，也沒有完整的理論，尤其是對于低模量合成纖維對混凝土徐變性能的影響仍缺乏研究。為此，本文選取清華大學生產的低模量合成纖維，研究了不同摻量低模量合成纖維對混凝土基本徐變的影響，并將試驗結果與混凝土徐變預測模型計算結果進行了比較，希望能為低模量合成纖維混凝土徐變預測模型的應用提供參考。

1 材料與試驗

1.1 材料

普通混凝土的配合比見表1，編號為F0。其中，水泥為42.5級普通硅酸鹽水泥；粗集料為石灰石，采用5～10 mm、10～20 mm和20～40 mm 3個級配，按照1∶3∶6的質量比進行配制；細集料為河砂，細度模數為2.7；水為普通自來水。在普通混凝土中分別摻入0.8 kg/m3、1.2 kg/m3和1.6 kg/m3的纖維即可得到相對應的纖維混凝土，工作性能試驗結果見表2，編號分別為F8、F12和F16。

表1 普通混凝土配合比 單位：kg/m3

表2 混凝土試件工作性能試驗結果 單位：s

本文選取的低模量合成纖維為清華大學國家“863”研究項目中的新型高性能合成纖維見圖1，纖維的具體性能指標見表3。

圖1 新型高性能合成纖維

表3 低模量合成纖維技術指標

1.2 試驗方法

1.2.1 力學實驗

參照《水工混凝土試驗規程》[14]，成型3組150 mm×150 mm×150 mm的立方體試樣，24 h脫模后移入標準養護室，達到28 d齡期后測量其抗壓強度。

1.2.2 徐變試驗

參照《水工混凝土試驗規程》[14]，每個配合比制作3個徐變試樣和2個補償試樣，試樣規格為Ф150 mm×450 mm。混凝土試樣澆筑振搗完成后，24 h進行脫模，并用紫銅皮密封以達到絕濕狀態，充氣法檢查密封性后移入(20±2)℃的徐變室。徐變儀器為彈簧式壓縮徐變儀，加荷齡期為28 d，加載荷載為對應齡期同尺寸試件軸心抗壓強度的 40%。量測設備為DI-25型差動式電阻應變計，加荷設備為油壓千斤頂，在加載后第1 d、7 d、30 d和90 d各調荷一次。

采用徐變度、徐變系數以及單位應力下的總壓縮應變來評價混凝土的徐變性能。其中，徐變度是指單位應力下的徐變變形，為徐變應變與持荷應力之比；徐變系數是指在恒應力作用下，試件某一時刻的徐變變形與其加載時刻的瞬時彈性變形的比值；單位應力下的總壓縮應變是指單位應力下的徐變變形與彈性變形之和，按式(1)[11]計算。

εc′=(1/Ec)+Cc

(1)

式中：εc＇為單位應力下的總壓縮應變，10-6；1/Ec為單位應力下的彈性變形，10-6；Cc為徐變度，10-6/MPa。

2 試驗結果分析

2.1 纖維摻量對混凝土力學性能的影響

F0、F8、F12和F16試樣28 d的立方體抗壓強度分別為42.61 MPa、42.82 MPa、43.50 MPa和42.25 MPa，可以看出立方體抗壓強度呈現先增大后減小的變化趨勢，F12的立方體抗壓強度最大，F16的立方體抗壓強度較F0略有下降，但影響幅度均在2%以內，說明該種纖維的摻入對混凝土28 d的立方體抗壓強度影響較小。

根據立方體抗壓強度與軸心抗壓強度的關系，換算系數取為0.53，各組混凝土試件軸心抗壓強度和加載荷載如表4所示。F0、F8、F12和F16的彈性模量分別為41.0 GPa、41.9 GPa、43.5 GPa和37.9 GPa，雖然也呈現先增大后減小的變化趨勢，但影響幅度均不超過8%，摻入纖維的混凝土試樣彈性模量與空白混凝土偏差較小。

表4 28 d軸心抗壓強度和加載荷載單位：MPa

2.2 纖維摻量對混凝土徐變的影響

徐變度、徐變系數以及單位應力下的總壓縮應變隨時間變化的曲線，見圖2～4。

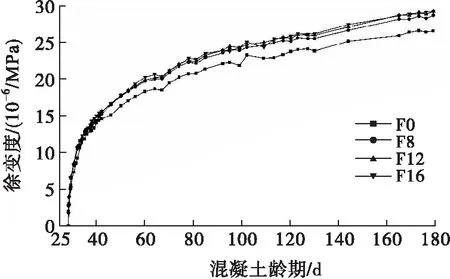
圖2 徐變度

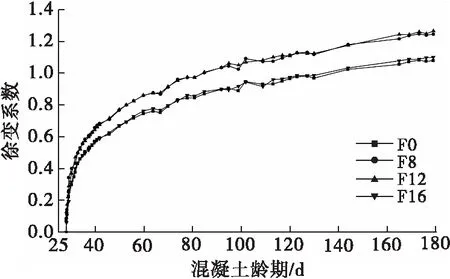
圖3 徐變系數

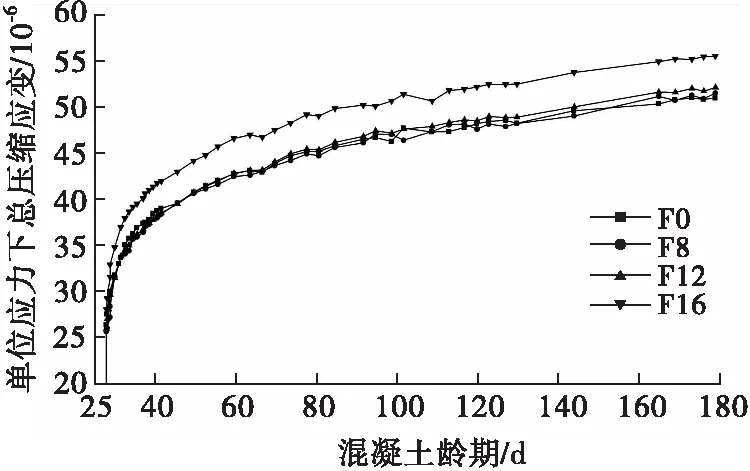
圖4 單位應力下的總壓縮應變

由圖2可以看出，隨著齡期的增長，混凝土的徐變逐漸增大，呈現出前期快后期慢的增長趨勢，這是因為混凝土承受荷載時，水泥漿體的徐變與加荷應力成正比，早期徐變發展較快，而后骨料會阻礙水泥漿體的流動，加載應力逐漸轉移到由骨料來承受，導致徐變速率逐漸減小[15]。F8、F12和F16的最終徐變度相比于F0分別增加了7.9%、10.1%和10.0%，表明低模量合成纖維的摻入增大了混凝土的徐變變形，主要原因是纖維的摻入增加了混凝土內部缺陷，加載狀態又造成凝膠吸附水和層間水遷移和滲出，延緩混凝土的水化[16]。低模量合成纖維不能像鋼纖維一樣抵抗混凝土的變形，從而增大了混凝土徐變。但在試驗纖維摻量范圍內，由于在加荷的往復過程中由纖維引起的部分孔隙被壓實，導致F12和F16的徐變差距不大。

由圖3可以看出，F8、F12和F16的徐變系數相比于F0分別增大了15.3%、17.2%和1.9%，在徐變度差異不大的情況下，說明F16和F8、F12的彈性變形差異明顯，F8和F12的彈性變形較F0分別減小了15×10-6、19×10-6，F16的彈性變形較F0卻增大了5×10-6，主要原因是合成纖維在混凝土中形成了較好的三維搭接結構，改善了微觀結構，提高了混凝土的韌性，但是過大的摻量導致纖維的重疊交織，對混凝土界面的弱化作用增強，增大了混凝土被“壓密”的可能性，對于混凝土基體而言是一種不容忽視的缺陷[15]。

由圖4可以看出，F8、F12和F16單位應力下的總壓縮應變相比于F0分別增加了1.1%、2.3%和8.9%，其相對大小關系與圖2有明顯差異，其原因在于徐變系數是以“除”的形式引入彈性變形，而單位應力下的總壓縮應變則是以“加”的形式引入彈性變形。F8、F12和F0的變化曲線基本重合，表明摻量在0.8～1.2 kg/m3范圍的低模量合成纖維雖然能提高混凝土的抗壓承載能力，但無法提高混凝土抵抗長期壓力變形的能力，而1.6 kg/m3的纖維摻量明顯降低了混凝土抵抗長期壓力變形的能力。

纖維對混凝土基本徐變的影響主要體現在兩個方面，一是對混凝土內部結構的影響；二是發揮混凝土內部變形的“阻擋”作用。纖維的摻入會增大混凝土的內部孔隙率[17]，增加混凝土內部的“多害孔”[18-19]，這些較大孔隙對混凝土基本徐變的影響隨時間變化呈現兩種作用，一是在加荷過程中孔隙增多給孔壁兩側C-S-H的滑移提供了更多的可能，同時會產生更多的初始微裂縫和缺陷，微裂縫會引起混凝土內部濕度的不平衡，導致毛細孔周圍的水分向毛細孔移動，進而引起周圍的水泥漿體干燥收縮，增大混凝土變形，而缺陷則會降低混凝土抵抗變形的能力；二是隨著水泥的進一步水化，混凝土中的孔隙逐漸變小，當縮小到毛細孔大小后，水泥的繼續水化便會引起混凝土進一步的收縮變形[20]。因此，在同等應力水平下，該種低模量合成纖維的摻入增大了混凝土的徐變。

3 徐變預測模型對纖維混凝土徐變的適用性

針對混凝土徐變的預測模型較多，使用廣泛的有雙冪函數模型、冪函數模型、對數函數模型和指數函數模型[21]，針對混凝土基本徐變的主要有CEB-FIP模型和GL-2000模型。本文將測試結果與上述模型擬合結果進行對比，其中，雙冪函數模型采用ACI-209R模型，對數函數模型采用CEB-FIP模型，GL-2000模型公式乘以修正系數m。擬合結果見表5，擬合曲線見圖5～8。

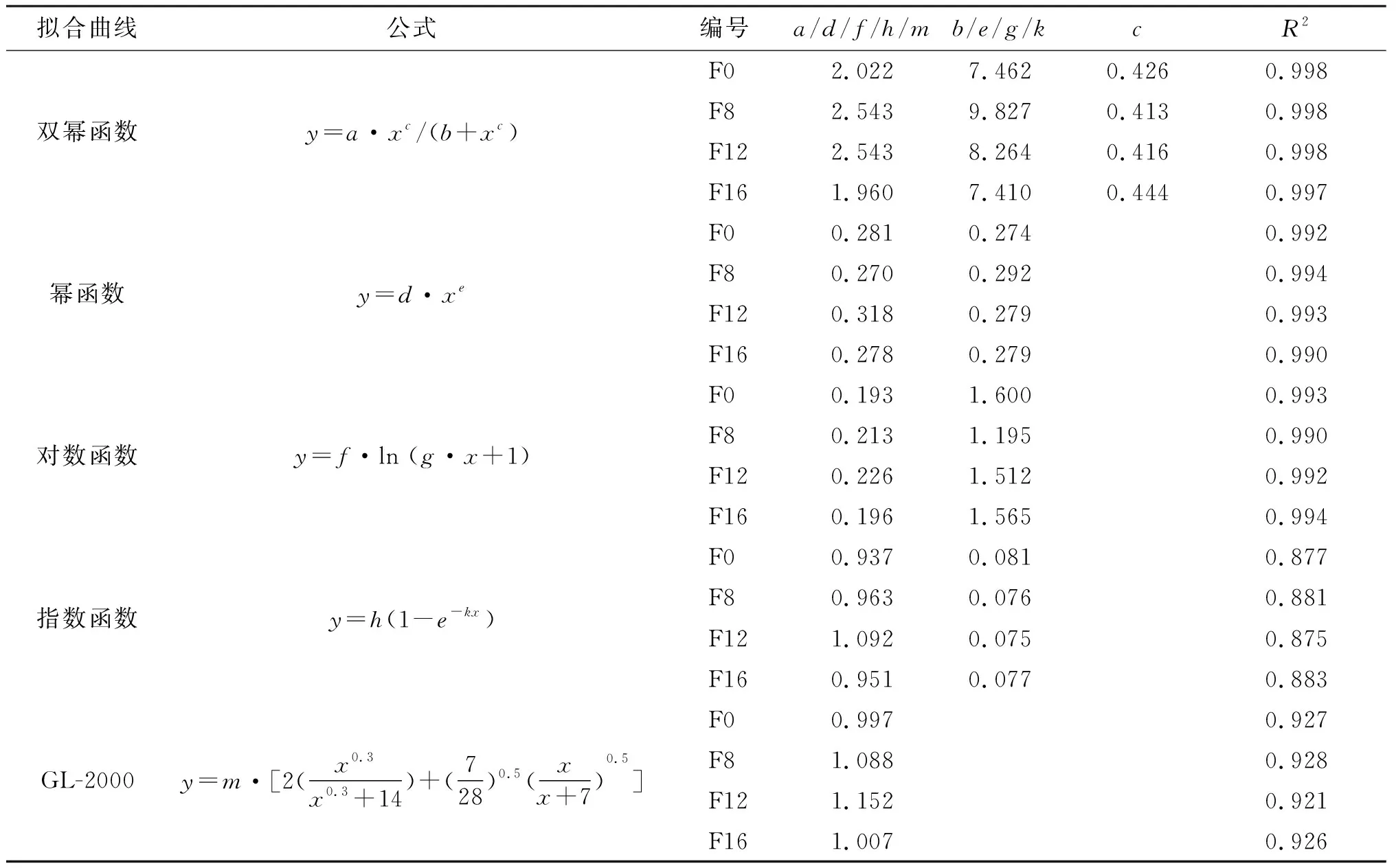
表5 徐變系數擬合曲線相關參數

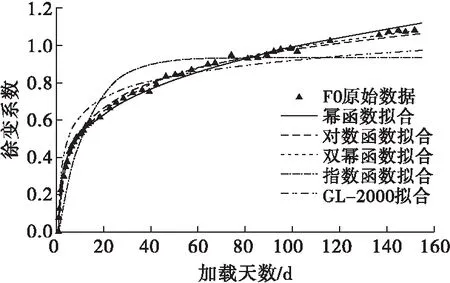
圖5 F0徐變系數擬合圖

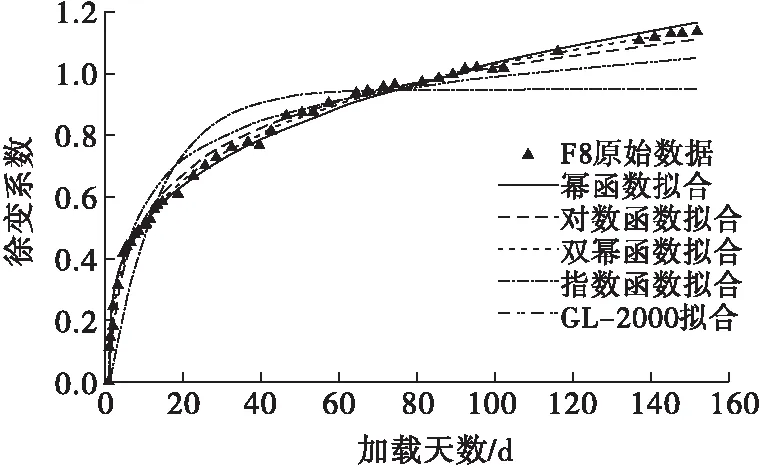
圖6 F8徐變系數擬合圖

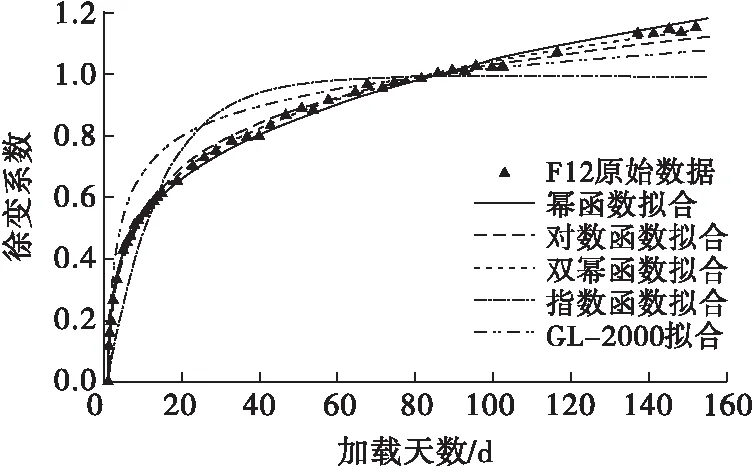
圖7 F12徐變系數擬合圖

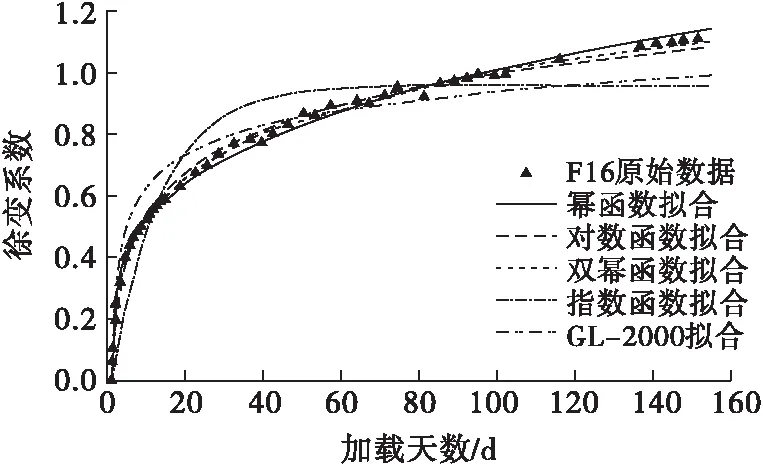
圖8 F16徐變系數擬合圖

由擬合曲線可以看出，對于混凝土前180 d齡期的徐變，雙冪函數的擬合效果最好，R2均大于0.997；對數函數和冪函數也有較好的擬合效果，R2均大于0.990，但對數函數后期曲線有低于實際曲線的趨勢，而冪函數后期曲線則有高于實際曲線的趨勢；指數函數的擬合效果最差，不適宜作為預測函數。GL-2000模型擬合后R2均大于0.92，擬合效果也不錯。根據擬合結果，本文對ACI-209R、CEB-FIP和GL-2000這3個模型的適用性進行進一步分析。

ACI-209R模型公式中，參數a為最終徐變系數，應在1.30～4.15范圍內；參數b和c是從試驗中獲得的擬合數據，應分別在6～30 d和0.40～0.80范圍內。雖然該公式主要針對混凝土的總徐變即基本徐變和干燥徐變之和，但根據擬合效果，其在基本徐變數據擬合上仍有很好的效果，且回歸參數值均在合理范圍內，因此認為ACI-209R可以作為低模量合成纖維混凝土徐變的預測模型。由于其相關參數無法根據材料性能和環境等進行計算，需要通過短期測試數據進行回歸。本文分別利用前14 d(16組)、前60 d(26組)和前100 d(38組)數據進行回歸，結果表明，F0、F8、F12和F16后續徐變系數的最大相對誤差均在7%以內，預測效果很好。

CEB-FIP模型公式按式(2)[13]計算。

(2)

式中：φbc為時間增長函數；fcm為混凝土28 d齡期的強度；t0,adj為調整后的齡期。

同樣，分別利用前14 d(16組)、前60 d(26組)和前100 d(38組)數據進行回歸，結果表明，F0、F8、F12和F16后續基本徐變度的最大相對誤差分別為17%、12%、9%和6%。

對于GL-2000模型公式，當修正系數m=1(即采用原公式)時，能夠直接計算混凝土的徐變系數，但60 d后的徐變系數，F0、F8、F12和F16的最大相對誤差分別為11%、12%、13%和12%。可以看出，GL-2000直接預測混凝土的徐變系數有較大的誤差，即使采用前100 d(38組)數據進行回歸，其后續徐變系數最大相對誤差仍達到了15%，因此認為GL-2000模型不適合用于低模量合成纖維混凝土徐變的預測。

4 結論

通過試驗數據的分析與討論，可以得出以下結論。

1)適量的低模量合成纖維能夠提高混凝土的強度和彈性模量，但當纖維摻量過大時，混凝土的強度和彈性模量均有所下降。

2)低模量合成纖維的摻入增大了混凝土的徐變變形，降低了混凝土抵抗徐變的能力，當纖維摻量為0.8 kg/m3、1.2 kg/m3和1.6 kg/m3時，徐變度分別增加7.9%、10.1%和10.0%。

3)當纖維摻量為1.6 kg/m3時，混凝土在反復加荷過程中出現較大的彈性變形，混凝土被“壓密”的程度較高，導致單位應力下的總壓縮應變出現明顯增長。

4)目前采用的混凝土徐變預測模型中，ACI-209R模型的效果最好，CEB-FIP模型也取得較好效果，但兩者均無法直接進行計算，具體參數需要利用短期試驗數據回歸得到。而GL-2000模型的預測結果誤差較大，不適合用于低模量合成纖維混凝土徐變的預測。