雙浮動密封橡膠O形圈接觸應力分析*
王永樂 謝 星 李 香 沈宗沼 丁思云
(合肥通用機械研究院有限公司 安徽合肥 230031)
工程機械設備、煤礦機械設備等長期工作在含泥沙顆粒等惡劣環境下,其旋轉動密封是十分關鍵的部件,直接影響著設備的可靠性和工作效率。目前采用較多的橡塑或聚氨酯材料唇形密封,在運轉過程中存在潤滑脂損耗嚴重、磨損失效和壽命短等問題。雙浮動端面密封由于其特殊的結構,可適用于泥沙等惡劣工況條件,且具有結構簡單、耐磨損、耐振動沖擊、密封性好以及壽命長等優點[1],目前已逐漸應用于掘進機滾刀、推土機履帶負重輪兩端及采煤機滾筒和減速器等工程機械密封系統[2-4]。
一般雙浮動密封是由一對端面硬度很高的金屬浮動動環、靜環及對應安裝的橡膠O形圈和浮封座構成,其結構對稱,通過O形圈軸向壓力壓緊形成端面密封。雙浮動密封裝置結構如圖1所示。其中,O形圈作為密封環的彈性補償元件,被摩擦力固定在浮封座內;同時其還具有輔助密封功能,這對雙浮動密封的運行起著非常關鍵的作用。許多學者對橡膠O形圈的受力進行了分析計算及試驗研究。李振濤等[5]利用ABAQUS軟件建立O形圈軸對稱模型,對不同工況下O形圈的應力分布規律進行分析,確定了O形密封圈材料易失效的位置。劉杰夫和呂曉仁[6]分析了盾構機密封O形圈靜態接觸下應力與壓縮率、流體壓力、硬度等的變化規律,但未能模擬真實結構參數,即不同斜面角度下的接觸模型。蔡智媛等[7-8]利用有限元軟件分析了軸安裝過程中O形圈的應力變化及對靜密封性能影響規律。SUKUMAR等[9]對不同硬度值的O形圈試樣進行了應力-應變數據測量,并作為有限元參數進行分析計算。SANG等[10]利用有限元軟件分析了液壓密封O形圈的軸向摩擦力、最大摩擦應力及接觸應力,并通過試驗測試驗證了數值計算的有效性。
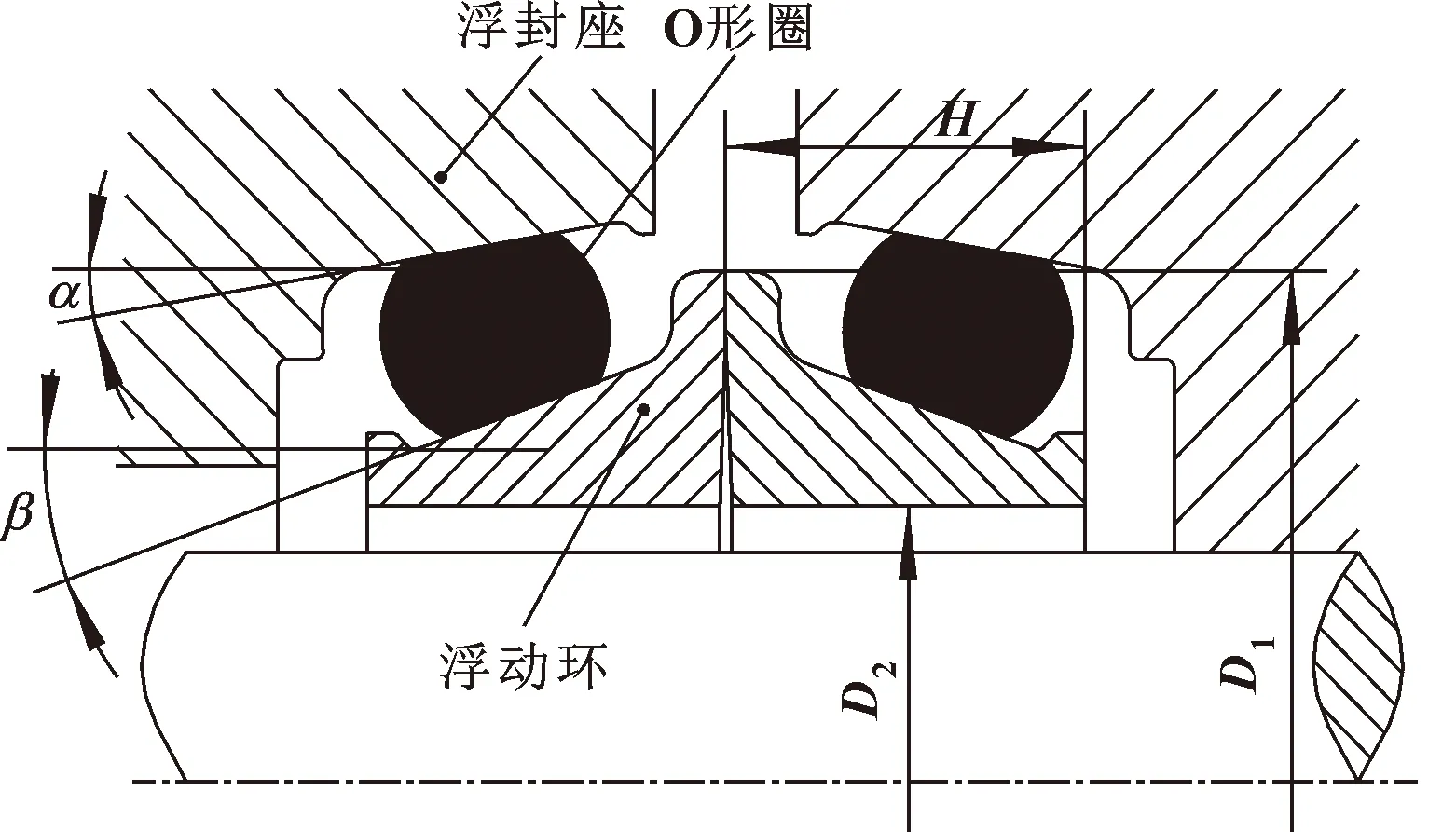
圖1 雙浮動密封結構示意
目前的研究針對O形圈平面壓縮較多,對具有一定傾斜角的接觸問題研究很少見。本文作者以雙浮動密封為研究對象,利用有限元方法開展不同浮封座和浮動環的斜面角度等對O形圈接觸過程應力影響的研究,為雙浮動密封結構設計提供理論指導。
1 計算模型
1.1 幾何模型
依據JB/T 8293—2014《浮動油封》標準的規定,選取公稱尺寸為220 mm×187 mm×19 mm的浮動環和浮封座作為研究對象進行分析,對應橡膠O形圈尺寸為φ200 mm×11.5 mm,浮封座斜面角度α=10°。O形圈初始位置分別與浮封座及浮動環相切。由于雙浮動密封結構的對稱性,文中將其簡化為二維軸對稱模型并取其一側進行分析。簡化后的幾何模型如圖2所示。
1.2 有限元模型
雙浮動密封結構參數、壓縮狀態等因素對O形圈的受力和密封性能起著關鍵作用。O形圈的應力分析計算屬于幾何非線性、材料非線性和狀態非線性的接觸問題,文中采用增廣拉格朗日接觸算法處理。其特點是:接觸壓力對于接觸剛度的敏感性降低,有利于在給定接觸剛度較大時計算收斂,也可以一定程度上提高計算精度。橡膠材料屬于超彈性近似不可壓縮體,其本構關系是復雜的非線性函數,通常用應變能函數表示。目前廣泛采用Mooney-Rivlin模型描述橡膠材料的應變能函數,同時附加體積約束能量項,得到修正的應變能函數[11]。文中采用雙參數的Mooney-Rivlin模型進行計算,其本構方程為
W=C10(I1-3)+C01(I2-3)
式中:I1、I2為應變張量的2個主不變量;C10和C01為材料常數。
根據相關標準[12]的推薦及工程應用經驗,文中選用邵氏A70度的丁腈橡膠為O形圈材料,其對應材料參數為:C10=0.739 MPa,C01=0.185 MPa[13]。
由于浮動環及浮封座的剛度遠大于橡膠材料,文中不考慮其變形,故將其設置為剛體。由于密封兩側壓差非常小,所以不考慮介質壓力的影響。為模擬安裝過程,將浮封座整體軸向壓縮率設置為S,浮動環端面設置為固定約束。將O形圈與浮動環背斜面及浮封座內斜面分別定義為2個接觸對,接觸類型設置為摩擦。橡膠與金屬件的摩擦因數初步設置為0.2[14]。進行網格劃分時,對O形圈進行了加密處理,將其單元尺寸設為0.4 mm。
2 計算結果及分析
2.1 壓縮率對O形圈應力的影響
圖3示出了O形圈在壓縮率S為4%~24%(軸向壓縮距離分別為2~12 mm)時的von Mises應力分布。可以發現:起初O形圈的最大應力分別出現在與2個剛體接觸位置附近;隨著壓縮率的增加,接觸帶寬度隨之增加,高應力區域不斷擴大并逐漸連通形成啞鈴型;隨著壓縮率的進一步增加,高應力區域逐漸縮小到中部形成橢圓形,并向外發散減小;壓縮過程中O形圈所受等效應力分布較均勻。但當壓縮率S=24%時,由于O形圈上部與浮動環接觸并發生擠壓變形,導致最大應力位置發生變化,右側分布偏多。
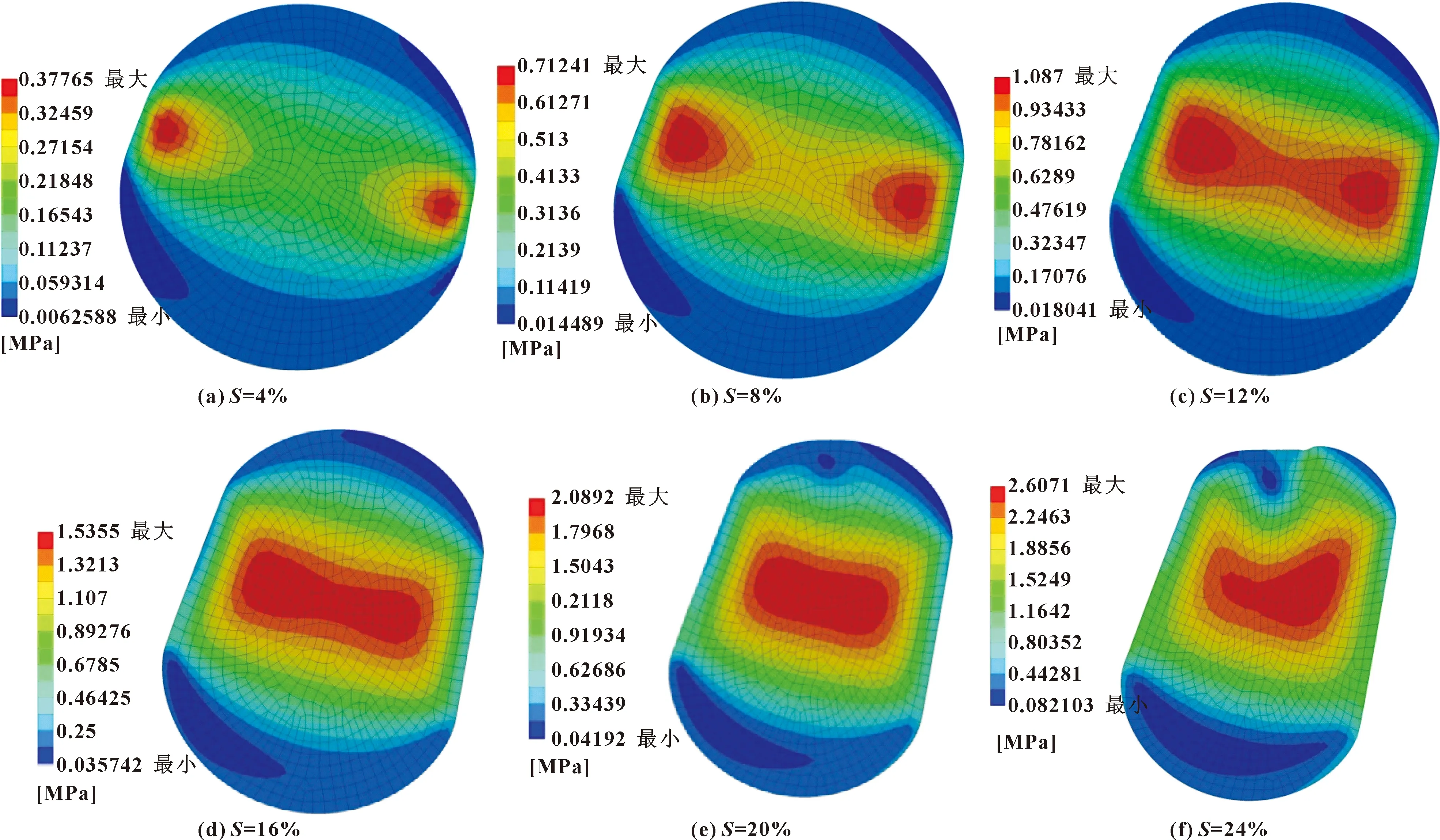
圖3 不同壓縮率S下的von Mises應力分布
圖4所示為O形圈在軸向壓縮率S為4%~24%時平面剪切應力分布。可以看出,隨著壓縮率的增加,最大剪切應力范圍由兩側開始的接觸位置附近向中間擴大,壓縮過程中高剪切應力始終處于有相對轉動的接觸部位前端位置。當S=24%時,由于O形圈上部與浮動環接觸,導致最大剪切應力位置發生變化,如圖4(f)所示,最大剪切應力位置主要集中分布于右側上部接觸位置附近。由于橡膠圈抗剪切變形能力遠小于其抗壓縮變形能力,所以最大剪切應力位置也反映了O形圈易出現損壞的部位。在設計中,應在滿足密封性能的前提下,盡量減小O形圈所受的最大剪切應力。
圖5示出了S=20%時O形圈整體位移情況。由于在整個壓縮過程中,兩側剛體對O形圈接觸部位產生摩擦、擠壓作用,使O形圈相對產生逆時針的轉動,最大位移出現在其右側與軸向移動的浮封座接觸位置的前端。接觸壓力反映的是O形圈與剛體接觸對間的壓力,其最大值反映了O形圈密封力的大小。當接觸壓力小于密封流體壓力時,接觸對間可能出現縫隙,導致泄漏量增大,使密封失效。圖6所示為壓縮率S=20%時對應的接觸壓力分布。可以發現:最大接觸壓力分別位于兩側接觸部分中心位置,并向外逐漸減小。此時,有利于油膜進入外部密封間隙,對密封起到一定的潤滑及散熱作用,最大密封力達2.4 MPa。
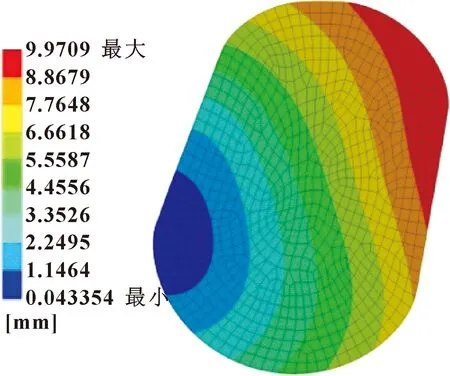
圖5 總變形(S=20%)
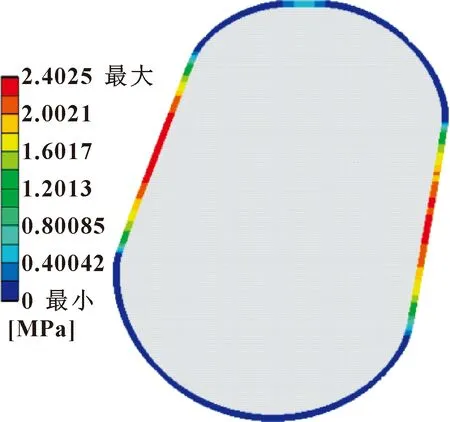
圖6 接觸壓力分布(S=20%)
圖7示出了各應力最大值隨壓縮率的變化。可知,最大等效應力與接觸壓力隨壓縮率的增大增幅相對較大,且二者的增長率相近,這說明壓縮率的增加能明顯提高O形圈的密封力。最大剪切應力也幾乎呈線性增加,但變化幅度相對較小。當S>20%時,剪切應力增幅明顯變大,此時不利于O形圈的受力。所以,在滿足密封力及端面比壓的前提下,要保持適當的壓縮率才能提高O形圈的使用壽命。而過大的壓縮率會使橡膠圈產生永久性變形、降低其彈性、加劇老化,進而引起密封失效。
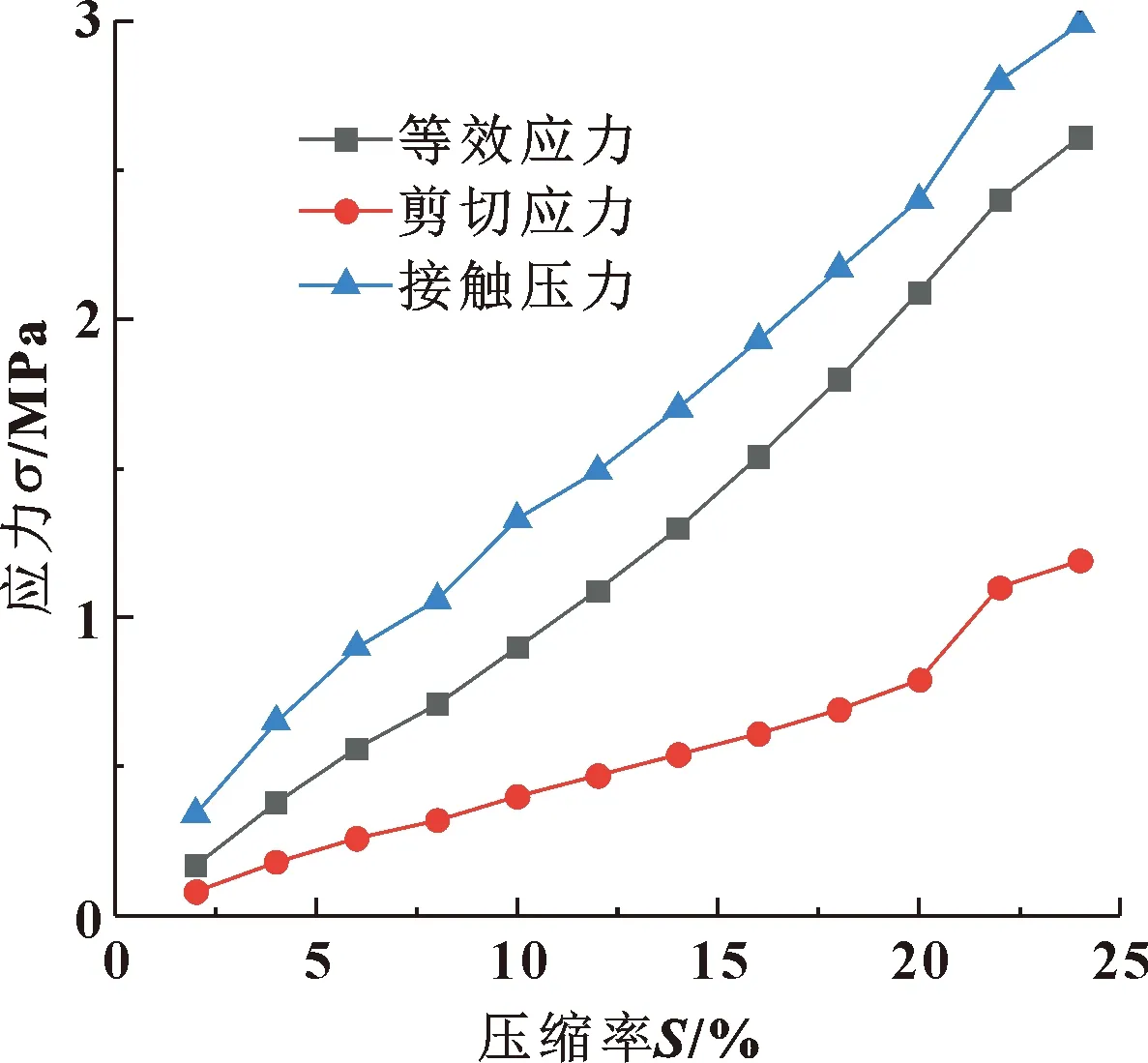
圖7 各應力最大值隨壓縮率的變化
對壓縮過程中O形圈與浮封環接觸位置的網格節點按逆時針順序從0~25進行編號,圖8所示為O形圈在不同的壓縮率下,左側接觸對不同節點編號上的接觸壓力。可見,接觸壓力均呈現拋物線形分布,最大接觸壓力位于接觸部位的中心處,其幅值隨著壓縮率S的增大而增大;隨著壓縮率S的增大,接觸部位發生了移動,接觸壓力范圍及數值也隨之增大。
2.2 結構參數對O形圈應力的影響
在浮動密封結構中,浮封座斜面角度α、浮動環斜面角度β是2個重要的結構參數,其角度的變化直接影響O形圈的受力。如圖9所示,在β=21°時,隨著浮封座斜面角α的增加,等效應力總體趨于減小,接觸壓力先減小后緩慢增加,而剪切應力整體變化較小,并在α=10°時處于最小。如圖10所示,在α=10°時,隨著浮動環斜面角β的增加,等效應力、接觸壓力呈遞增趨勢,但剪切應力上下波動,整體變化不明顯,在β=21°時,剪切應力最小。
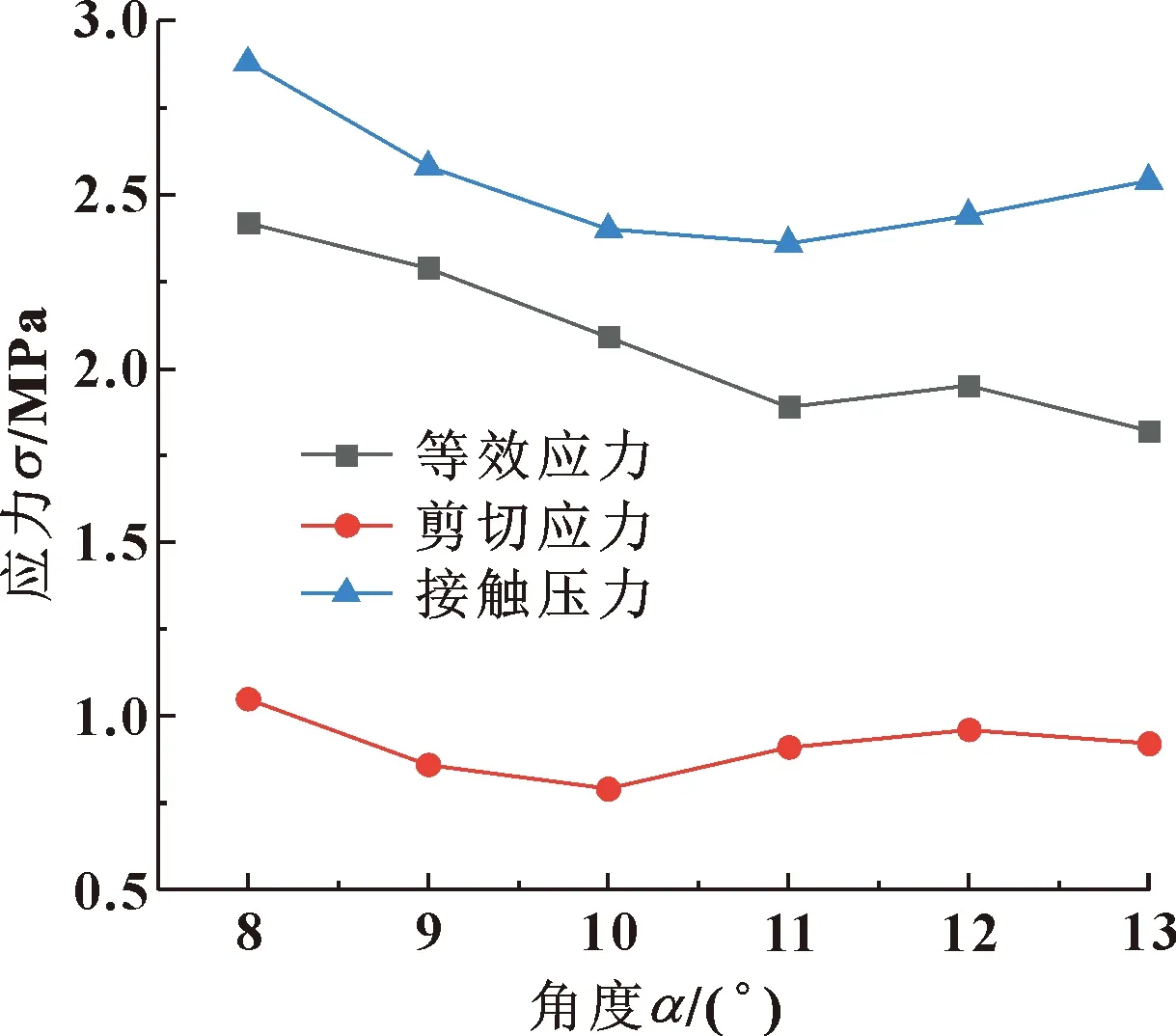
圖9 浮封座斜面角度α對應力的影響(β=21°)
最大剪切應力最小時,O形圈最不易發生剪切失效[6]。所以,當α=10°、β=21°時,在保證密封性能的同時,有利于O形圈的受力。

圖10 浮動環斜面角度β對應力的影響(α=10°)
2.3 摩擦因數對O形圈應力的影響
為保證橡膠O形圈能夠傳遞足夠的扭矩而不打滑,浮動環的背斜面與浮封座的內斜面需具有一定的表面粗糙度,一般推薦值為Ra6.3~12.5 μm[15]。圖11示出了浮動環的背斜面與O形圈間的摩擦因數對O形圈應力的影響。可以發現:當O形圈與接觸斜面的摩擦因數取0.1~0.4時,對于O形圈應力的影響很小,可以忽略不計,所以在進行密封設計時并非粗糙度值越大越好。
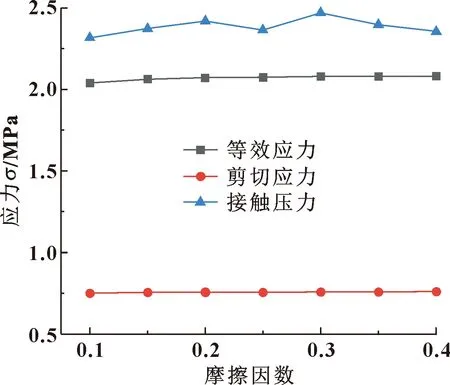
圖11 各應力隨摩擦因數的變化
3 結論
(1)隨著雙浮動密封橡膠O形圈壓縮率的增加,其各接觸應力最大值呈線性增大,高應力分布區域由接觸位置附近向中間擴散并逐漸連通;接觸壓力呈拋物線形分布于兩側的接觸對間,最大接觸壓力位于O形圈接觸部位的中心處。
(2)浮封座斜面角α和浮動環斜面角β對O形圈等效應力和接觸壓力影響較大,對剪切應力影響較小。在接觸壓力滿足密封要求的前提下,根據最大剪切應力最小確定了浮封座和浮動環斜面角的最優值分別為α=10°、β=21°。
(3)在不考慮介質壓力影響的情況下,O形圈與接觸斜面的摩擦因數在一定范圍的取值對O形圈各應力的影響很小,可以忽略不計。

