基于子模型法的牽引梁結構優化設計

曾子銘，孫麗萍，王玉艷，孫業琛，盧佳妮

(大連交通大學 機車車輛工程學院，遼寧 大連 116028)

隨著我國鐵路行業的快速發展，特別是客運專線和高速鐵路的相繼開通，工程軌道車的投入量逐漸增長.在機車車輛設計制造過程中，車體結構的靜強度計算不僅可以對車體結構的強度和剛度進行校核、指導結構改進，而且在提高機車車輛運營可靠性方面也發揮著重要作用[1-2].車輛在運行過程中，牽引梁主要用于傳遞軌道車輛縱向拉伸或壓縮載荷，能夠將來自車鉤裝置的縱向力傳遞到底架，其結構可靠性直接關系到車輛的運營安全[3].因此，在設計階段對牽引梁進行高效的強度校核是一項必不可少的工作.

本文針對牽引梁后蓋板在強度校核中安全系數不滿足設計要求的問題，采用子模型法和拓撲優化對其結構開展優化研究.這樣不僅減小計算規模，提高了設計效率，同時可為 未來相關板類的設計提供有益參考.

1 牽引梁結構簡介

牽引梁是車體底架車鉤安裝和車輛承載的重要結構，其前端與緩沖梁連接，后端與枕梁連接，左右兩側分別通過小橫梁與底架邊梁焊接在一起.其主要構件由上蓋板、腹板、隔板、加強筋板、后蓋板和托板等組成，材質均為耐候鋼(Q345)，結構如圖1所示.

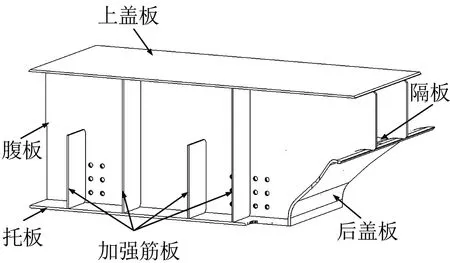
圖1 牽引梁結構

根據設計要求，結構強度需小于材料的屈服極限且安全系數需大于等于1.1.牽引梁結構確定后，對其進行靜強度分析時發現：壓縮工況下，強度的最危險部位發生在牽引梁后蓋板，數值為335.5 MPa，雖然應力值小于材料的屈服極限，但是其安全系數為1.03，不滿足設計要求.因此，為了提高設計效率，結合子模型法對其結構重新進行優化設計.

2 子模型法簡介

子模型法基于圣維南原理，是在計算分析整體模型基礎上，對局部部件采取相關研究的一種方法，同時子模型法也被稱為切割邊界或特定邊界位移法.切割邊界指的是將所研究的部件的邊界從整體模型中分割出來，獲得的位移信息作為子模型基本的邊界條件[4]，進而將子模型從整體模型中提出來開展下一步的研究.子模型法可以從有限元理論中得到證明，而有限元求解的本質是線性方程組求解，具體可以表達為：

[K][D]=[F]

(1)

式中,[K]為整體剛度矩陣，[D]為待求的位移向量，[F]為外載荷.

假設位移向量[D]中，已知部分為[D1]，其余部分為[D2]，則上式可以改寫為

(2)

其中,式(2)展開可以得到：

K22·D2=F2-K21·D1

(3)

由此可知，位移向量[D1]已經轉變為載荷項，進而可求得向量[D2]，其中位移向量 [D1]即為切割邊界的位移條件，這就從有限元理論角度驗證了子模型法的正確性[5-6].

子模型法不僅保證了局部部件研究的準確性，也使得結構在優化研究過程中的計算量大幅度減小，進而縮短了研究人員的設計時間，提高整體的分析效率，達到了以較小的計算量實現局部結構優化的目的.

3 牽引梁子模型

根據子模型法的基本理論，將整車模型中的牽引梁提取出來，建立牽引梁子模型.具體步驟如下：

首先對整車的有限元模型開展靜強度計算，得到各個工況下的應力和位移結果.基于整車有限元模型的計算結果，將牽引梁從整車有限元模型中截取出來，同時建立牽引梁子模型的相關單元集合和邊界的節點集合，獲得邊界位移信息后刪除與牽引梁子模型不相關的網格.其次將牽引梁視為單獨模型開展細化研究.將獲得的邊界條件和位移信息重新施加到模型中，設置載荷約束從而得到牽引梁子模型.

獲得牽引梁子模型后，為了確保子模型的準確性，對其進行靜強度計算加以驗證，通過對比牽引梁子模型和整車模型的強度和剛度可以得出：在壓縮工況下的最大VonMises應力值和發生的位置以及剛度基本保持一致，因此通過驗證可以認為牽引梁子模型符合要求，具備優化研究的條件.

牽引梁結構整體采用殼單元離散，尺寸大小為20 mm，最終生成了12 446個節點和12 305個單元，其有限元模型如圖2所示.

圖2 牽引梁有限元模型

4 牽引梁后蓋板拓撲優化

4.1 拓撲優化

拓撲優化指的是尋找優化設計區域內結構材料的最優分布，在給定邊界條件、載荷以及滿足各項設計約束的基礎上，最終達到設計目標最優的目的[7].該方法可以在設計初期或工程探索階段為設計人員提供結構和材料的最優分布方案，設計人員依據優化結果對設計方案作出相應的調整.經過多年的發展，常見的拓撲優化方法有：均勻化方法、變厚度法、變密度法、漸進結構優化法等[8-9].

本文以變密度法為理論基礎，將區間[0，1]內的密度值作為設計變量.其中0、1表示材料的去除和保留[10].通過此方法就可以實現結構的拓撲優化問題和材料的最優分布問題之間的轉換，同時將拓撲變量依附于單元材料上，進而基于連續變量的優化算法進行計算，在得到了最佳的傳遞力的路徑同時，也使得最終的設計方案更加合理、經濟[11].

4.2 牽引梁后蓋板結構拓撲優化

牽引梁原設計結構中，后蓋板的板厚為17 mm，質量為59.93 kg.由于只有牽引梁后蓋板在壓縮工況下的安全系數，不滿足設計要求，因此只需對牽引梁后蓋板進行優化即可，所以在參考原設計結構的外形尺寸基礎上，將牽引梁后蓋板以及腹板和隔板連接處采用實體網格填充，填充后的實體網格數量為30 348，得到了優化設計區域實體填充模型，其如圖3所示.為了計算結果更加準確，部分網格重新劃分，局部區域采用三角形網格進行過渡.最終以生成的實體網格為設計區域進行拓撲優化，數學模型可以描述為：

圖3 優化設計區域實體填充模型

(1)目標函數：質量分數最小化；

(2)設計變量：牽引梁后蓋板實體單元的密度；

(3)約束條件：給定設計區域的VonMises應力小于310 MPa.

通過OptiStruct計算顯示，牽引梁后蓋板模型結構在經過99次迭代后收斂，其目標函數的迭代曲線如圖4所示.

圖4 目標函數迭代曲線圖

優化過程結束后，其結果在HyperView中打開，通過改變不同的密度閾值以獲得優化后材料分布和載荷傳遞路徑的最佳效果.通過改變不同的閾值，可以得到不同密度閾值下的等值面圖.當密度閾值為0.5時，其等值面圖如圖5所示，從中可以清晰地看到材料分布情況，同時也得到了牽引梁后蓋板的整體的外形形狀以及與腹板連接的筋板.通過測量網格的尺寸，得到后蓋板的厚度為16.75 mm，圓整后板厚取17 mm.后蓋板的板厚與原設計結構的厚度保持一致.

圖5 密度閾值為0.5時密度等值面圖

根據優化結果對牽引梁后蓋板進行幾何重構，同時綜合考慮后蓋板與其他各結構焊接關系，對牽引梁后蓋板結構重新設計，得到的結構見圖6所示.設計后的牽引梁后蓋板與原設計結構相比，其與牽引梁托板連接處的弧度有所增加，而且在水平方向的傾斜角度更大.

圖6 幾何重構后的牽引梁后蓋板

牽引梁后蓋板結構改進之后，其強度是否滿足設計要求還不清楚，因此將優化后的牽引梁后蓋板放到整車模型中進行應力計算和分析.從計算結果可以看出：在壓縮工況中，改進后的牽引梁后蓋板的最大VonMises應力為303.2 MPa，小于材料屈服極限，達到了設計要求中規定的安全系數大于等于1.1的要求.同時最大應力發生的位置與原設計結構基本一致，其應力分布見圖7所示.由此可以證明優化后的結構滿足設計要求.

圖7 改進后牽引梁后蓋板應力云圖

結合優化后牽引梁后蓋板應力云圖可以看出：優化后的牽引梁后蓋板中間部位應力較小，材料存在冗余，可以適當去除部分質量，這在加工工藝上是很容易實現的.于是在保證后蓋板外形尺寸的前提下在其中間增加減重孔，這樣既減少了設計材料，又降低了結構質量，同時間接地節約了制造成本，最終得到牽引梁后蓋板結構如圖8所示.增加減重孔后的牽引梁后蓋板在整車中的靜強度計算結果為：與未增加減重孔的牽引梁后蓋板相比，在壓縮工況中最大VonMises應力發生的位置一致，但是應力值從303.2 MPa增加到305.9 MPa，盡管應力值增加了2.7 MPa，但是依然滿足材料的屈服極限且安全系數達到1.13，顯然結果滿足設計要求，其應力云圖如圖9所示.此外，增加減重孔的牽引梁后蓋板的質量為53.26 kg，與原設計結構相比，質量減少了6.67 kg，減重11.13%.而且在壓縮工況下的最大位移由原來的5.23 mm變為5.29 mm，剛度變化不大.

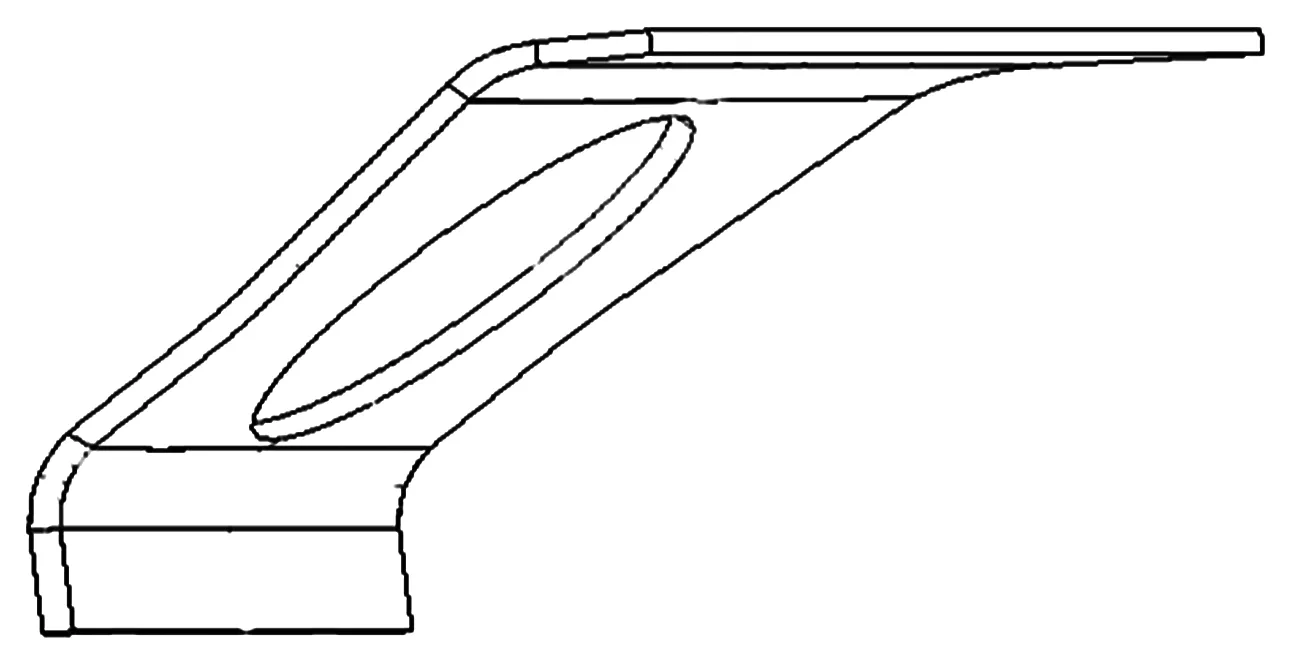
圖8 增加減重孔后的牽引梁后蓋板

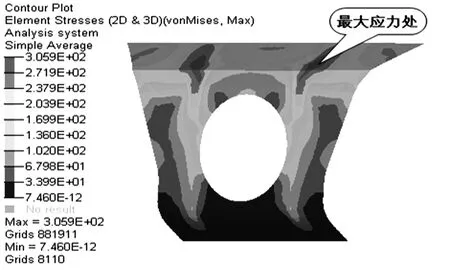
圖9 增加減重孔后的牽引梁后蓋板應力云圖

牽引梁后蓋板通過拓撲優化、幾何重構以及增加減重孔后，確定了最終的設計方案.此方案不僅在壓縮工況下滿足設計要求，同時在其他工況下，改進后的牽引梁后蓋板結構也符合設計要求.因此可以認為該方案達到了設計的預期目的.

5 結論

本文以某工程軌道車牽引梁后蓋板為研究對象，利用子模型法對其進行拓撲優化.在設計過程中，子模型法的應用大幅度縮短了計算時間，而且計算精度也得到了保證.實現了以較小的計算量達到牽引梁后蓋板結構優化的準確計算.同時依據拓撲優化的分析結果對牽引梁后蓋板的結構進行重新設計，得到了最優方案，該方案經過整車靜強度計算，安全系數達到1.13，滿足設計要求.同時其質量比原設計結構減少了6.67 kg，減重11.13%，輕量化效果明顯.