多元LDPC編碼調制系統CNN輔助迭代檢測譯碼算法

萬 飛，白寶明，朱 敏

(西安電子科技大學 綜合業務網理論及關鍵技術國家重點實驗室，陜西 西安710071)

0 引言

近年來，深度學習(Deep Learning,DL)已經在圖像處理、機器翻譯、語音識別等領域展現出了顯著的性能提升，也在通信領域收到了廣泛的關注。DL在物理層的典型應用包括模型/數據驅動的檢測、均衡和譯碼。

當前，將DL應用到譯碼中已經成為學術界和工業界的廣泛認同。文獻[1]將神經網絡(Neural Network,NN)引入到信道譯碼(BCH碼)中，其展現的優異性能激發了DL與譯碼結合的研究熱潮。隨后，越來越多基于DL的譯碼方案被提出[2-3]，例如，自編碼器[4]和不同類型的NN譯碼方案的性能分析[5-6]。同時，DL與經典算法的結合也被視為另一種有效利用深度學習能力的方案。文獻[7] 基于置信傳播譯碼算法與NN的結合，將因子圖上的權重視為分枝重要性度量，剪枝低重要性的因子圖分枝，對于Reed-Muller碼和短LDPC碼取得了良好的比特錯誤率(Bit Error Rate,BER)性能，并且顯著降低了譯碼復雜度。其他傳統譯碼算法，比如最小和譯碼算法及偏移最小和算法[8]通過NN給因子圖增加乘性訓練權重和偏移參數減少了近似誤差，也取得了性能提升。而針對相關噪聲的影響，文獻[9]在二元LDPC碼中使用卷積神經網絡(Convolution Neural Network,CNN)來輔助收端抵抗噪聲的影響，同樣的方案也被采用輔助Polar碼譯碼[10]。當下，大部分的工作都集中在二元碼上，并且除了基于掩模圖的方案[11]，其他所有方案都受限于信息長度，基本都在中短碼長下使用[12]。

而一般來說，在等效比特長度下，相較于二元LDPC碼，多元LDPC碼有著更小的生成矩陣和更優異的誤碼性能。因此，神經網絡的規模隨著碼長的增長呈指數增長的限制對于多元碼不再是困難。并且，多元LDPC碼天然適合與高階調制相結合的特性也使得其更具有實用性。但是，軟判決譯碼算法的復雜度太高，這是限制多元LDPC碼實用的最大問題。在文獻[13] 中，對于加性高斯白噪聲(Additive White Gaussian Noise,AWGN)信道傳輸的符號使用sinc脈沖成形，提出一種基于硬消息傳遞的多元LDPC碼聯合檢測譯碼迭代(Iterative Joint Detection Decoding,IJDD)的方案。

本文考慮到更實際的場景，在發端使用了平方根升余弦(square-Root Raised-Cosine,RRC)脈沖成形濾波器。對于AWGN信道，在收端也使用對應的RRC濾波器和適當的采樣。因此，端到端的等效離散模型可以視為信號經歷了一個相關噪聲信道。同時，文獻[14]及后續的工作也展現出了一種全新的角度——從噪聲的角度考慮譯碼的方案。基于相關噪聲的特性，采用DL來減弱噪聲的影響以提升傳輸的性能。

本文提出了一種CNN輔助的迭代檢測譯碼(Iterative Detection and Decoding,IDD)框架，可以有效抵抗相關信道噪聲。NN從接收序列中恢復出相關噪聲，然后迭代地從接收序列中減去學習到的噪聲數據，減弱了噪聲影響的信號能夠得到更好的BER性能。并且，受利用NN譯碼方案的啟發，在CNN輔助的IDD方案(CNN-IDD)后再級聯一個網絡，可以達到進一步的性能提升。

1 基礎原理

1.1 多元LDPC碼

在中短碼長下，多元LDPC碼的性能優于二元LDPC碼，尤其是與高階調制相結合時。然而，軟判決譯碼算法的高復雜度限制了其實際使用。在文獻[19-20]中，基于硬信息的IJDD譯碼算法被提出，在復雜度與性能之間實現了良好的平衡。IJDD算法的基本思想是采用硬消息迭代將信號檢測器和多元LDPC譯碼器融為一個整體，在信號空間上通過多次迭代將有噪接收信號逐步修正到正確信號點上。此后，基于符號投票準則的大數邏輯算法被提出[13,21]。

1.2 深度學習(DL)

DL在圖像分類、語言處理和機器翻譯等方面的巨大成功引起了跨領域合作的熱潮。常用的NN包括多層感知機、CNN和循環NN，本文使用CNN來輔助譯碼。

如圖1所示，神經網絡從左到右分別由輸入層、隱藏層和輸出層組成。

圖1 NN結構圖

輸入層將數據集傳入NN，因此，其包含的神經元數目與數據集的特征數一致。對應地，輸出層將預測結果傳出NN，其包含的神經元數目與標簽維度一致。隱藏層是整個NN最為重要的部分，對應于第i層的操作為：

zi=g(i)(wixi+bi)，

(1)

其中，zi為當前層的輸出，xi為第i-1層的輸出zi-1。wi和bi分別為第i層的權重矩陣和偏置向量。激活函數g(·)給NN引入了非線性，也是DL強大表達能力的原因之一。常用的兩種激活函數——線性整流(Rectified linear unit,Relu)和sigmoid函數如下所示：

(2)

另一種重要的函數是損失函數，它衡量了模型預測與真實標簽之間的差異，比如均方差(Mean Square Error)損失函數：

(3)

因為其在像素圖上強大的特征提取能力，CNN被廣泛應用在圖像處理中。如圖2所示，CNN利用卷積操作從部分像素點中提取特征。

圖2 CNN處理框圖

卷積核對于數據的復用能夠減少數據集規模需求，同時也會加速訓練過程。后續的池化操作能夠避免過擬合。

2 CNN輔助的迭代檢測譯碼框架

2.1 系統模型

結合CNN-IJDD的多元LDPC碼編碼調制系統框圖如圖3所示。

圖3 CNN-IDD傳輸框圖

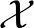
如圖4所示，經過RRC脈沖成形，等效離散時間信道輸出為:

圖4 等效離散時間信道模型

y=x+n，

(4)

式中，噪聲n是擁有自相關矩陣R的復高斯隨機向量。令Ri,j為R的第(i,j)個元素，則

Ri,j=ρ|i-j|，

(5)

式中，ρ為相關系數。這樣的信道模型在文獻[22] 中也被引用。

(6)

zHT=0。

(7)

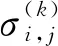
(8)

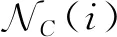
因此，估計的噪聲序列為：

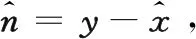
(9)

這就是NN的原始數據。

CNN在獲取噪聲序列之后，利用實/復數轉換、卷積和非線性函數等操作，在損失函數和標簽指引下進行訓練。

2.2 級聯網絡的CNN-IDD優化結構

受NN可以直接用于譯碼的啟發，在CNN-IDD迭代后再級聯CNN網絡，得到圖5的優化CNN-IDD結構，對最后一次迭代的譯碼器輸出再經過一次CNN網絡修正來輔助CNN-IDD框架的譯碼輸出。

圖5 優化的CNN-IDD傳輸框圖

2.3 數據處理和CNN設計

將原始數據傳入CNN時，簡單地將復數向量直接聯合，得到類似圖像的矩陣是不合理的。考慮到實際通信傳輸中復數信號的特點，如圖6所示，對應圖3中的紅色虛線框，利用實部虛部分離和重構的預處理操作。

圖6 CNN設計流程

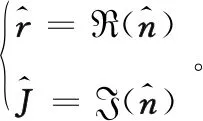
(10)

通過此操作，訓練所需要的數據集數量可以減半。將實部與虛部按列放置組合構造得到數據矩陣。

由于池化操作和輸出層前的全連接結構在本文提出的方案中會引起較大的性能損失，因此并不推薦采用。為了得到與標簽向量相同的特征維度，設定最后一層隱藏層中卷積核的水平滑動步長為2，其余層中水平滑動步長均為1。垂直滑動步長由超參數設定，CNN的詳細處理過程如算法1所示。

相對應的，在輸出層后，需要將預測數據按照下式，進行實部虛部重新組合，整合為復數形式，即網絡學習到的噪聲序列：

(11)

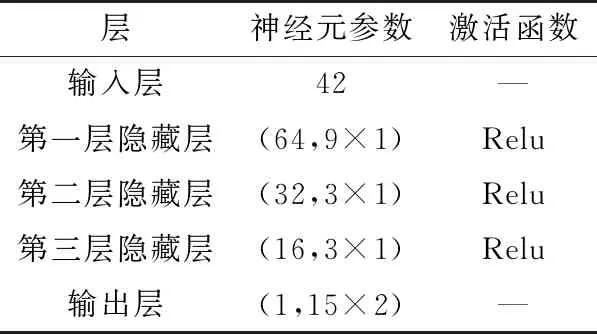
算法1 CNN處理過程輸入:數據集:r^,J^特征向量:R(n),I(n)網絡參數:長度n,批量大小Bz,卷積層數L,每一層神經元數目[a0=0,a1,…,aL]和濾波器大小[b1,b2,…,bL]目標:輸出估計噪聲r^,J^1:將r^,J^傳入輸入層;2:將輸入向量轉化為(Bz,n,0,1)形式張量;3:fori∈[1,L] do4:令卷積核大小為[bi,1,ai-1,ai];5:使用步長[1,1,1,1]移動卷積核fori

3 仿真結果與分析

3.1 參數設置

在訓練階段，本文使用在多個信噪比[8 dB,18 dB,0.5 dB] 下生成的數據，對于每個信噪比生成200 000個符號，其中90%用于網絡訓練，剩下的用于測試。模型共使用5層網絡，每一層的神經元數目和激活函數設置如表1所示，其中“(a,b×c)”指的是通道數目a和卷積核大小b×c。利用Xavier初始化[24]、Adam優化算法[25]和MSE損失函數,設定學習率為0.01，衰減率為0.99。訓練的截止條件設定為損失不再下降或者達到最大迭代次數5 000次。為了提高模型對于信噪比的穩健性，使用了批量歸一化，對于每個信噪比下選取了50個樣本。同時，也采用了0.001的正則化和0.999的滾動平均來改善模型的泛化能力。

表1 CNN參數設置表

3.2 性能與分析

圖7比較了多元LDPC碼硬判決譯碼和僅采用CNN的譯碼性能，對于BER=10-4時，CNN方案可以取得約1 dB的性能增益,這也驗證了優化的CNN-IDD方案的出發點。

圖8展現了迭代次數對于BER性能的影響。可以看到，對于BER=10-4時，2次迭代和10次迭代的CNN-IDD方案分別取得了0.5 dB和0.4 dB的性能增益。對10次迭代下僅采用一次網絡調用而不是每次IDD后都調用網絡的做法，在保證性能的前提下進一步降低了復雜度。

圖8 CNN-IDD方案在不同迭代次數下的性能

圖9比較了CNN-IDD方案和優化的CNN-IDD方案性能，對于2次迭代，優化的CNN-IDD比原IJDD算法取得近1 dB的性能增益，比CNN-IDD方案取得了0.5 dB的性能增益。

圖9 優化的CNN-IDD性能

4 結束語

本文針對多元LDPC碼編碼調制系統，提出了CNN-IDD方案及其優化來減小相關信道噪聲影響。通過從接收信號中刪除CNN預測噪聲的迭代操作，收端減弱了噪聲對于信息的影響，從而給檢測和譯碼提供了經過去噪處理的數據，即改善了接收信號的信噪比。仿真結果表明，對于GF(64)域上的(42,21)多于LDPC碼，優化的CNN-IDD算法可以取得近1 dB的性能增益。后續，將考慮更高域上的多元LDPC碼的CNN-IDD方案，同時將信道擴展至衰落噪聲信道和碼間干擾信道。